频变黏弹性流体因子叠前地震F-AVA反演方法

李 坤, 印兴耀, 宗兆云, 刘元坤, 李志超

(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580; 2.中国石油集团东方地球物理勘探有限责任公司,河北涿州 072750)

依据地震数据的流体识别,即利用地下介质单一弹性参数、组合形式或孔隙流体模量等一系列敏感流体指示参数对孔隙含流体特征进行描述和定量表征,而叠前地震AVO/AVA(amplitude variation with offset/angle)和EI(elastic impedance)反演是弹性参数预测的有效途径[1]。复杂双相介质情况下,岩石孔隙流体的存在会引起地震波的衰减和频散,尤其在含烃储层中传播时,这种衰减现象更为明显[2]。为充分利用地震资料蕴含的振幅和频率异常信息,低频阴影[3-4]、衰减特征[5]、频散属性[6]等逐渐被用来进行储层含流体性质检测。国内外学者提出多种孔裂隙含流体岩石物理模型,试图从机制上明确储层中流体的存在对地震波衰减及频散现象的影响,同时为开展频变流体识别奠定理论基础[7-9]。Wilson等[10-11]依据Chapman多尺度裂缝频散岩石物理模型,利用拓展的两项频变Smith-Gidlow近似式,率先提出了频变AVA反演的概念(F-AVA);张世鑫等[12-13]将叠后反射系数和Shuey近似公式拓展为频率依赖,提出纵波速度频散梯度的概念,研究了基于地震数据的频散属性孔隙流体识别方法。程冰洁等[14]研究了频变AVA属性之间的关系,将频变AVA流体识别技术应用到低孔低渗碎屑岩储层的含气性识别中。张震等[15]基于Russell近似公式构建了频变流体项f,研究了基于连续小波多尺度分解的频变流体因子AVA反演方法。李坤等[16]提出了基于匹配追踪高分辨率谱分解算法的时频域F-AVA (Frequency dependent AVA)反演方法,旨在改善“子波叠印”去除误差和频变属性反演的分辨率。然而,当前的频散属性反演和流体识别应用仍集中于完全弹性介质假设情况下的叠前AVA反射方面,大多数是常规AVA非频变反射公式的一种广义频变拓展,并未真正依据衰减介质的频变AVA反射特征方程展开。笔者利用Futterman常Q衰减模型来考虑地下介质的黏弹性[17-18],且构建频变黏弹性流体因子(FDV-FI),推导含频变黏弹性流体因子的F-AVA反射特征方程;依据贝叶斯理论和先验正则化推导黏弹性F-AVA反演的映射方程和目标泛函;利用叠前部分角度叠加道集实现基于F-AVA反演的砂岩储层含油气性识别。

1 频变黏弹性流体因子叠前地震F-AVA反演原理

1.1 黏弹性介质频变反射系数

考虑介质黏滞性来模拟地震波的衰减和频散效应,运用Futterman近似常Q模型描述黏弹性介质中纵横波复速度(α,β)随频率的变化特征[17-18],其中利用相速度和品质因子定量表征的复速度如下:

(1)

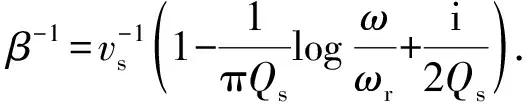
(2)

式中,Qp和Qs分别为纵波品质因子和横波品质因子;vp和vs分别为参考频率ωr对应的纵横波相速度。黏弹性介质的平面波散射方程与完全弹性介质的反射形式一致,差异在于5个波(入射P波、反射P波和SV波、透射P波和SV波)的传播速度、波数、振幅均为复数,使非弹性介质的平面波传播特征异于弹性介质[18],非弹性介质Aki-Richard纵波反射系数为

mpp(θ,ω)=a(θ)[Δα/α(ω)]+b(θ)[Δβ/β(ω)]+

c(θ)[Δρ/ρ].

(3)

其中

a(θ)=(1+tan2θ),

(4)

其中

(5)

(6)

将式(5)、(6)带入式(4)中,可得

(7)

由于黏弹性纵波反射mpp(θ,ω)含虚部项,假设弱非弹性情况,则虚部项为相对小量,将其忽略得实反射系数为

mpp(θ,ω)=

(8)

式(8)即基于Futterman黏弹模型构建的黏弹性AVAF线性近似方程。为验证该黏弹性反射特征方程的精确度,本文中采用双层模型计算单界面黏弹性AVAF反射系数,模型参数见表1。基于Futterman黏弹模型的精确Zoeppritz方程、常规Russell近似方程和本文推导的黏弹AVAF近似方程计算得到的反射系数如图1和2所示。

表1 黏弹性介质频变双层模型Table 1 Frequency-dependent two-layer model for viscoelastic media

黏弹性介质中叠前AVA反射系数随着频率的变化发生变化,如图2(a)、(b)所示(其中,mZoepp(θ,ω)表示黏弹性介质精确Zoeppritz方程),当频率ω≠ωr时,黏弹性反射的实部和虚部都是频率依赖的,然而虚部的反射振幅相比实部AVA反射振幅较小,因此本文中忽略弱小虚部反射。图2(c)、(d)所示为黏弹性AVO近似方程的频变反射特征与误差分析。由图2可见,本文中构建的黏弹性频变AVA反射系数(式(8))与黏弹Zoeppritz方程的实部保持较好的一致性,进而说明该近似方程在黏弹性频变流体因子提取方面的可行性。

图2 黏弹性AVA近似方程的频变反射特征与精度分析Fig.2 Frequency-dependentcharacteristics and accuracy analysis of viscoelastic AVA approximation equation

1.2 黏弹性频变流体因子反演

目前,利用叠前地震振幅和频率信息的频变AVA反演均是建立在完全弹性介质假设情况下进行的[10-16],即平面谐纵波入射到两半无限弹性介质的Zoeppritz近似公式的的频变AVA拓展应用。本文中在黏弹性AVA近似方程(式(8))推导的基础上,提出了基于F-AVA反演的黏弹性频变流体因子提取方法。针对式(8)求取频率ω的偏导数得

(9)

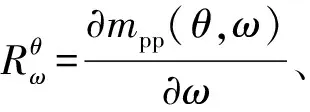
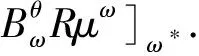
(10)

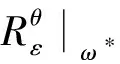
(11)

(12)

当Δω=ωi+1-ωi在较小范围波动,假设Sθ,ωi+1≈W(θ,ω*)*mpp(θ,ωi+1),Sθ,ωi≈W(θ,ω*)*mpp(θ,ωi),则式(11)可以重新组织为

Sθ,ωi+1-Sθ,ωi≈ΔωiW(θ,ω*)*[A(θ,ω*)Fω*+

(13)

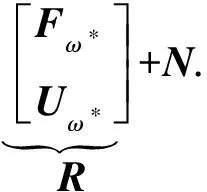
(14)

其中

A(θi,ω*)=diag[A(θi,ω*)],

B(θi,ω*)=diag[B(θi,ω*)].

(15)

(16)

(17)

其中

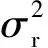
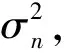
(3) 采用共轭梯度算法求解方程(16)的最优解Rk-1。

(6) 输出频变黏弹性属性的最优模型参数Fω*、Uω*。

2 理论数据分析

为了验证频变黏弹性流体因子叠前地震F-AVA反演方法的可行性和抗噪声能力,本文中利用重采样后的实测弹性参数、30 Hz零相位Ricker子波及黏弹性AVA近似方程式(8)合成叠前地震数据,图3所示为理论流体因子f、剪切模量μ,密度ρ和纵波品质因子Qp(注:横波品质因子Qs>100)。图4所示为含不同噪声情况下的合成地震数据和黏弹性频散属性反演结果(无噪声、RSN=5、RSN=2及RSN=1),其中黑色为依据Futterman近似常Q模型计算的频变黏弹性流体因子和频变剪切模量,绿色虚线为初始模型,红色虚线为黏弹性频散属性Fω*和Uω*的反演结果。

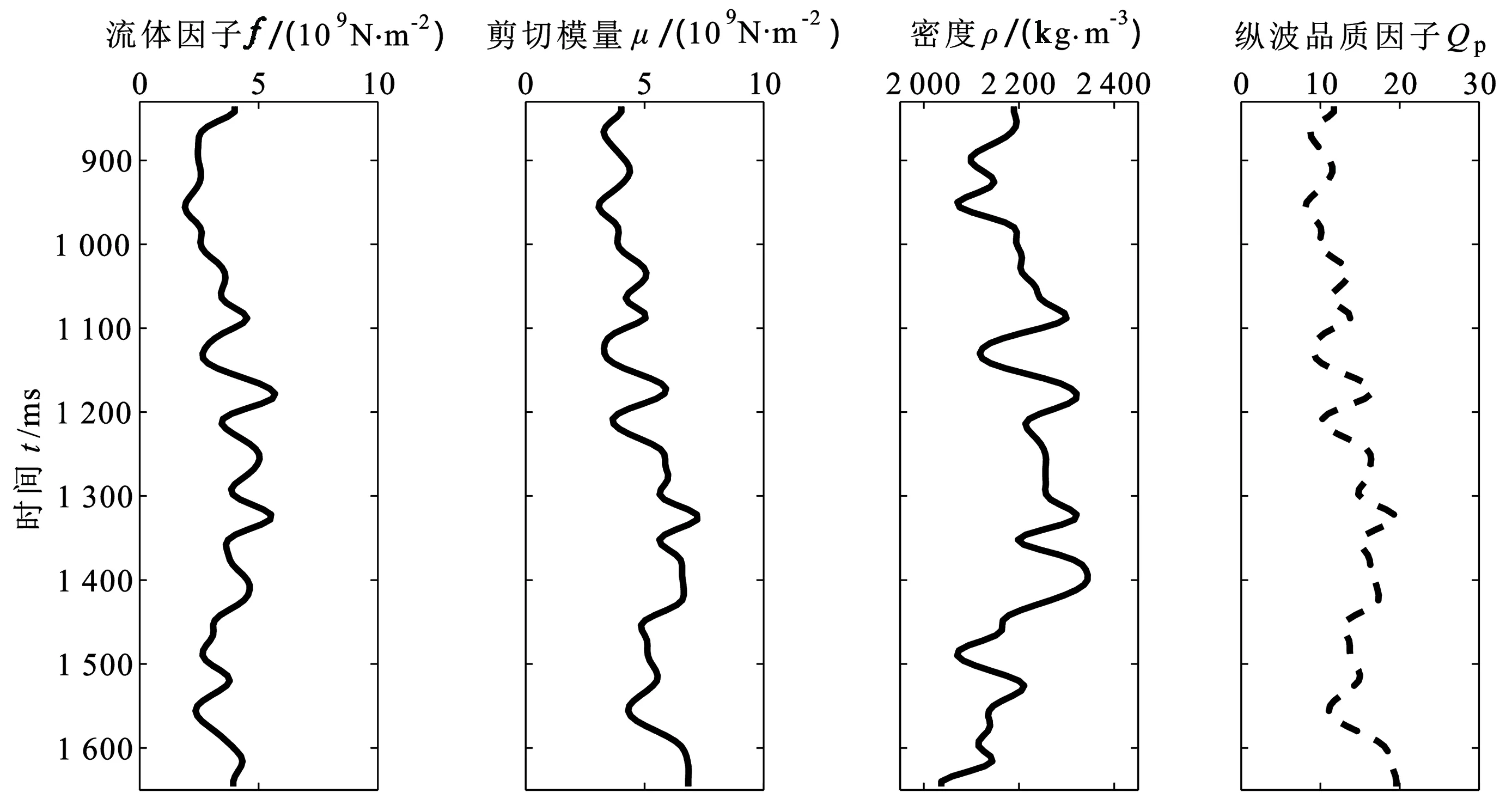
图3 理论流体因子f、剪切模量μ,密度ρ和纵波品质因子Qp模型Fig.3 Theoretical fluid factor f, shear modulus μ, density ρ and P-wave quality factor Qp

从图4(a)、(b)中可见,理论叠前地震反射振幅不仅随着入射角度的变化发生变化,且在黏弹性介质的假设下,其同样随着频率的变化发生明显变化,故此为黏弹性频散属性的F-AVA反演预测提供了有效的数据基础。同时,依据本文中提出的黏弹性频散属性F-AVA反演算法预测得到的频变黏弹性流体因子Fω*与理论数值保持较高的一致性,即使在RSN=2和RSN=1噪声情况下也可以实现理论频散模型的高吻合度评价。然而,对比本算法中频变黏弹性参数Fω*和Uω*的反演精度可以看出,频变黏弹性剪切模量Uω*的反演精度比频变黏弹性流体因子Fω*的预测精度相对较低,尤其当地震数据在受到强噪声(RSN=2和RSN=1)干扰时,频变黏弹性剪切模量Uω*的预测精度将大大降低,究其原因是由于横波品质因子Qs>100,其横波的衰减和频散程度相对较小。本文中主要关注频变黏弹性流体因子Fω*在含油气储层流体识别中的应用,可靠的频变黏弹性流体因子Fω*预测结果验证了该黏弹性F-AVA反演算法的有效性和抗噪能力。

3 实际资料处理

为了验证该频变黏弹性流体因子F-AVA反演方法的实用性,在理论模型验证该方法可行性的基础上,针对中国东部K勘探工区的实际地震资料进行了处理。如图5所示为过LM井的的部分角度叠加实际地震剖面,其中入射角度依次为12°、21°和30°,采样间隔为2 ms,剖面中黑色曲线所示为电阻率Rs测井曲线(浅双侧向电阻率测井结果在油藏发育位置为异常高值,如图中黑色箭头指示位置),H1和H2为研究区目的层。

首先通过对LM井旁道数据频谱分析可知,高信噪比有效频带范围为10.2～63.5Hz。本文中选取f0=31 Hz为最优参考频率,利用MPQ-WVD(快速匹配追踪谱分解方法)对中角度地震数据进行谱分解,提取f=15、25、40 Hz的单频瞬时谱分量,如图6(a)～(c)所示。由图6中可见,15Hz单频谱中在油藏下方(白色椭圆区域)存在明显的“低频阴影”异常现象,随着频率分量的不断升高,油藏下方低频强能量团逐渐消失,“低频阴影”现象的产生为后续频变黏弹性流体因子的反演提供佐证,但单频剖面中存在很多“虚假亮点”,故仅依靠“低频阴影”对孔隙流体进行判识将会产生干扰。

频变黏弹性流体因子反演综合利用了叠前反射数据的频率和振幅异常响应,图7(a)～(c)依次为频变黏弹性流体因子、频变黏弹性剪切模量、常规频变流体因子[16]及归一化高频瞬时谱衰减梯度的反演结果。其中,高频瞬时谱衰减梯度是利用中角度地震数据(图5(b))的单频瞬时谱f=56、40、31 Hz计算得到,即求取单频振幅谱的高频能量随频率的衰减速度。由图7中可见,归一化的频变黏弹性流体因子(图7(a))、常规频变流体因子(图7(c))和高频瞬时谱衰减梯度属性(图7(d))在油藏区域(如箭头所示)均呈现异常高值,与实测电阻率解释结果吻合较好,且反演剖面的频变异常不明显,验证了该方法的有效性。然而,高频瞬时谱衰减梯度和常规频变流体因子的反演剖面(图7(c))中却存在较多“虚假亮点”干扰,尤其是高频瞬时谱衰减梯度(图7(d))相比频变黏弹性流体因子FAVA地震反演的纵向分辨率较低,在精确识别油气藏发育位置方面存在挑战,在保证相同叠前反演算法的情况下,黏弹性流体因子fvis的频散程度Fω*的油层指示敏感性将大幅度提高(如图7(a)和(c)中黑色椭圆和箭头所示),进而说明了频变黏弹属性相比常规频散属性能够更好地表征储层孔隙内的含烃性质。

图4 不同信噪比RSN情况下的合成地震数据和黏弹性频散属性反演测试Fig.4 Synthetic seismic data and estimated results of viscoelastic dispersion attributes with different signal to noise ratio RSN

图5 中国东部K研究区内的部分角度叠加地震道集Fig.5 Partial-angle stack seismic gathersfrom K explorationarea in east of China

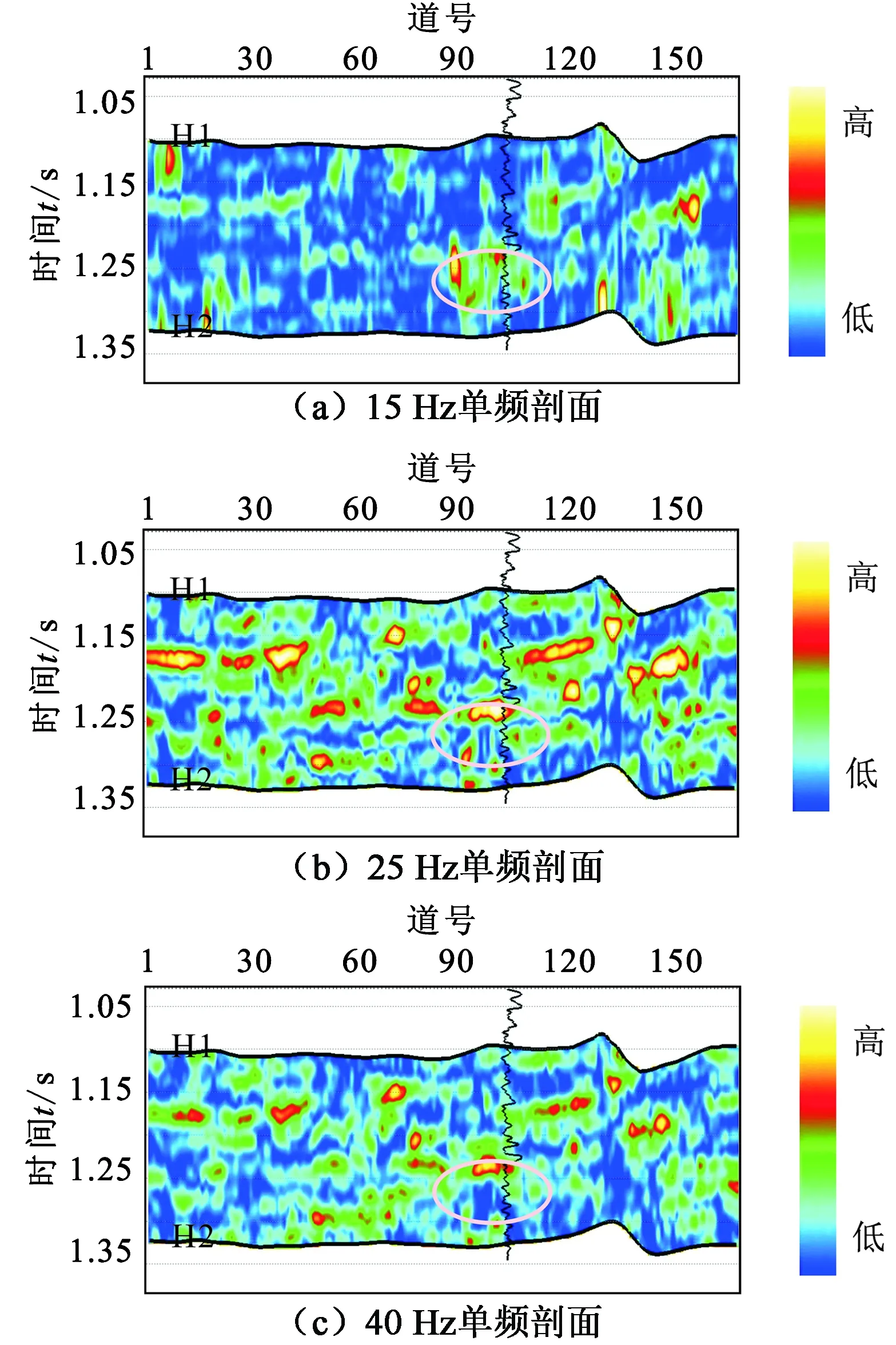
图6 中角度地震数据的匹配追踪单频谱剖面Fig.6 Iso-frequency instantaneous spectrums of middle-angle seismic gathers based on matching pursuitspectral decomposition

图7 频变黏弹性流体因子和常规频散衰减属性的实际应用效果分析Fig.7 Analysis of practical application effect of frequency dependent viscoelastic fluid factor and conventional dispersion-attenuation attributes

4 结束语

通过在频变AVO/AVA叠前地震反演中引入Futterman近似常Q模型,提出了基于贝叶斯F-AVA反演算法的频变黏弹性流体因子预测方法。频变黏弹性流体因子叠前反演是常规频变AVA反演的一种拓展,其综合考虑了地下介质黏滞性对地震波AVA反射特征的影响,且黏弹性频率依赖的AVA近似为该F-AVA反演的关键理论基础。通过理论模型将本文中推导的黏弹性近似方程与基于Futterman常Q模型的精确Zoeppritz方程进行了对比,验证了该F-AVA近似公式具有较高的精度。关于反演算法方面,联合贝叶斯公式和先验模型正则化项构建了反演映射矩阵和目标泛函,模型测试说明了该方法在提取黏弹性频散属性方面的可行性和抗噪性。最后本文中将该F-AVA反演方法应用于实际地震数据的处理和储层流体识别测试,通过与匹配追踪单频地震剖面、常规频变流体因子及高频瞬时谱衰减梯度属性的应用效果对比发现,该频变黏弹性流体因子的反演结果中具有更少的“虚假亮点”干扰,在储层孔隙烃类检测方面将具有更高的预测精度。