滑动窗口中FP-Tree的频繁项集挖掘算法的研究

李芬田,王红梅,潘 超

(长春工业大学 计算机科学与工程学院,长春 130012)

1 引 言

数据流[1]的应用越来越广泛,比如我们常见的网络监控、股票的交易、网络通讯的监控、传感器网络和天气或环境的检测都会生成大量的数据流.随着数据流应用的普及,数据流环境下的数据挖掘越来越引起人们的兴趣,又因为数据流中的频繁项集又是数据流挖掘中最基本的问题之一,所以近十几年得到许多学者的研究,但是由于数据流具有连续、无限、快速、随着时间变化且不可预知的等特性,从而在数据流环境下挖掘频繁项集带来了很大的挑战.近几年来大量的数据流频繁项集挖掘算法被学者们陆续提出[2-5].其中最典型的是Han等人提出的FP-Growth算法[6],Manku等人提出的estDec算法[7],Leung等人提出的DSTree算法[8]和Giannella等人提出的FP-stream算法[9],FP-stream算法将最近的频繁项集保存在倾斜时间窗口里,将旧的频繁项集以粗糙的时间粒度保存,设计了Pattern-tree来维护频繁模式信息,进而实现数据流上频繁项集的挖掘;Lee等人提出WMFP-SW算法[10]和刘学军等人提出的DS-CFI算法[11]是在FP-Growth算法上的改进实现了频繁项集的挖掘,但是这两个算法在处理稠密数据集时动态更新的速度比较慢;李国徽等人提出的DSFPM算法[12]能动态的挖掘出滑动窗口内的完全频繁项集,但是DSFPM-Tree中大量的父子节点存在不频繁的关系时,建立的DSFPM-Tree比较高,并且树中分支多,最关键的是窗口在滑动时,需要频繁的更新DSFPM-Tree,导致时间开销比较大;Deypir等人提出的pWin算法[13]采用前缀树存储频繁项集,用反向深度遍历挖掘频繁项集,但是当有大量的事务插入或删除时,频繁的访问前缀树比较浪费时间.

本文针对以上算法的不足,提出了滑动窗口中FP-Tree的频繁项集挖掘算法MFI-SW(A frequent itemset mining algorithm in the sliding window),MFI-SW算法将数据流分块挖掘,采用上三角矩阵存储,在内存中用NCFP-Tree保存每个基本窗口中的临界频繁项集,窗口滑动阶段只需要将旧的NCFP-Tree删除,建立新的NCFP-Tree即可,然后采用优化的算法挖掘每个基本窗口中临界频繁项集,进而挖掘出完全频繁项集.

2 问题描述

定义1[14].(数据流):设I={I1,I2,…,In}是项的集合,Ii表示第i项(1≤i≤n),数据流DS是一组连续不断到达的数据序列{T1,T2,…,Tn}的集合,Tj表示第j个到达的事务(1≤j≤m),对于任意Tj都有Tj⊆I.

定义2[4].(滑动窗口):将数据流中的数据分成大小相等的块,这样的每个分块是一个基本窗口,记作w.每块中包含的事务个数是基本窗口的大小,记作|w|.k个连续的基本窗口组成一个滑动窗口W,记为W=〈w1,w2,…,wk〉,k值是预先固定的.滑动窗口的大小指的是每个滑动窗口中基本窗口的个数,记为|W|.

支持度[14]:∀X⊆I滑动窗口中包含项集X的事务个数称为X的支持度计数,记为S,若sup(X)=S/|w|,则sup(X)称为X在w中的支持度.

定义3.(频繁项集,临界频繁项集,非频繁项集):对于用户给定的最小支持度阈值为ζ和误差因子为ε,假设|W|(|w|)表示滑动窗口W(基本窗口w)的大小.在滑动窗口W(基本窗口w)中模式A的支持度计数用fW(A)(fw(A))表示.如果满足fW(A)≥ζ|W|(fw(A)≥ζ|w|),就称模式A是滑动窗口W(基本窗口w)中的频繁项集.如果满足fW(A)≥(ζ-ε)|W|(fw(A)≥(ζ-ε)|w|),则称为模式A是滑动窗口W(基本窗口w)中的临界频繁项集.如果满足fW(A)<ε|W|(fw(A)<ε|w|),就称模式A是滑动窗口W(基本窗口w)中的非频繁项集.

性质1[14].假设X是非频繁项集,那么它的任何超集都是非频繁项集.

性质2.在NCFP-Tree中的父亲和孩子组成的2-项集包含临界频繁2-项集的全部信息.

证明:因为在构建NCFP-Tree时,只有插入节点和某个祖先节点能够组成临界频繁2-项集才可以插入,否则删除该结点.

性质3.项目矩阵PM中包含频繁1-项集和频繁2-项集的全部信息.

定理1.每个基本窗口中的非频繁项集被删除后,尽管它们在整个滑动窗口中,是频繁的,其中输出支持度的误差也不会超过ε,是可以接受的.

证明:设|w|表示一个基本窗口的宽度,|W|表示滑动窗口的长度,设定最小支持度阈值为ζ和误差因子为ε,如果模式A在滑动窗口中是频繁的,则满足fW(A)≥ζ|W|,如果在基本窗口wi(1≤i≤k)中是临界频繁的,则满足fwi(A)≥(ζ-ε)|wi|.如果在基本窗口wj(1≤j≤k)中是非频繁的,则满足fwj(A)<ε|wj|.因此,fW(A)=∑fwi(A)+∑fwj(A),所以对模式A支持度为fW(A)=∑fwi(A)=fW(A)-∑fwj(A)≥ζ|W|-∑ε|w|≥(ζ-ε)|W|.因此得证,由定理1知,仅仅保存每个基本窗口中的临界频繁项集,就可以满足在误差允许的范围内输出的项集是滑动窗口中所有的频繁项集.

3 MFI-SW算法描述

3.1 MFI-SW算法的数据结构

该算法的数据结构包含3种,分别是项目矩阵(PM),临界频繁模式树NCFP-Tree和频繁项集表(FI-i_List).

1)项目矩阵(PM):PM为上三角矩阵,每行或每列存储数据库中项的集合,其中项目矩阵中元素PM(i,j)的值表示出现的次数.

2)临界频繁模式树NCFP-Tree,由根节点(用null标记)、临界频繁项集构成的前缀子树和临界频繁项头表三部分组成.

除了根节点之外的每个节点是由5个域组成的(itemname,support,parent,child,nextnode),其中itemname表示项名,支持度计数用support表示,指向父节点的指针用parent_link表示,指向孩子节点的指针用child_link表示;指向树中具有相同项名的下一个节点的指针用nextnode_link表示.

临界频繁项头表ID_List中每个元组包含2个域(It_id,link),其中It_id表示基本窗口中临界频繁1-项集的项名,link表示链头指针,指向NCFP-Tree中有相同项名的第一个节点,需降序排列每个基本窗口中项的支持度计数.

3)FI-i_List():一种数组结构,包括k+2个域(Item,F1,F2,…,Fk,F),其中Item表示项名,Fi表示第i个基本窗口挖掘的临界频繁项集的支持度计数,F表示滑动窗口中项集的支持度计数的和.为了提高时间效率,将挖掘出来的临界频繁项集分开存储,临界频繁i-项集存储在FI-i_List中,其中(1≤i≤n).该表起始状态为空,将挖掘的基本窗口中临界频繁项集存储在对应的表中,关键的步骤是当窗口滑动时,将挖掘的新本窗口中的项集直接覆盖旧基本窗口中对应的项集即可.

3.2 NCFP-Tree的构造方法

它由根(用“NULL”标记)、临界频繁项集构成的前缀子树和临界频繁项头表三部分组成,创建NCFP-Tree的根结点,对DS中的每个事务进行如下处理:

1)选择Ti中的临界频繁项,并将它们按临界频繁项头表顺序排列,第一次扫描项集,设排序后的临界频繁项集列表为[p|P],其中p是第一个项目,而P是剩余的项目列表.

2)调用insert_tree([p|P],T).

注意:函数insert_tree([p|P],T)执行如下:

在插入节点之前,扫描项目矩阵PM,首先判断插入结点与祖先节点组成的2-项集是否为临界频繁2-项集,如果有一个祖先节点M与该节点组合成的2-项集满足临界频繁2-项集,则该节点可以作为M的孩子节点插入,如果不满足临界频繁2-项集,那么一层一层的向根部搜索,直到有一节点q,它和插入节点组成的二项集的支持度满足临界频繁项集的条件.但如果一直到根节点NULL都没有节点与该节点能组合为临界频繁2-项集,那么剪掉该节点.如果能找到该节点,插入时需要进行下列操作:判断T是否有子女,如果T有子女N使N.item=p,N的计数就加1,否则需要创建一个新的节点N,将item设置为p,sup设置为1,链接到它的父节点,并通过节点链Node_link链接到具有相同项名的节点上.

3)如果P不为空,递归调用insert_tree(P,p).

3.3 MFI-SW算法描述

1.窗口初始阶段

输入:数据流DS,滑动窗口W的大小为m,基本窗口大小为|w|,最小误差因子ε

输出:项目矩阵PM,每个基本窗口对应的NCFP-Tree

1)滑动窗口中含m个基本窗口,基本窗口大小为|w|

2)for(i=1,i<=m,i++){

3)调用函数Creat_PM生成项目矩阵PM

4)调用算法Creat_NCFP-Tree,生成m个NCFP-Tree树}

函数Creat_PM如下://项目矩阵的构造

1)PM[i,j]=0 //初始化矩阵PM,n为项的个数

2)for each Ti in DS //扫描事务数据库,构建PM矩阵

3)for each ei in Ti

4)for each ej in Ti

5)if j>=i

6)PM[i,j]++

7)for i=1 to n // n代表基本窗口的平均长度

8){count=0

9)for j>=i+1 to n

10)if PM[i,j]<ε|w|

11)delete ei

12)// ei是不频繁项,删除支持度不符合条件的项}

2.窗口滑动阶段

输入:新基本窗口中的事务数据流,最小误差因子ε,滑动窗口W的大小为m

输出:更新的项目矩阵PM和新基本窗口的NCFP-tree

1)调用函数Creat_PM建立新基本窗口的项目矩阵

2)调用Creat_NCFP-Tree生成新基本窗口的NCFP-Tree树

3)调用函数Update_FI-i_List更新频繁项集表

对表都进行更新,函数Update_FI-i_List如下:

1)int column = t%m //t表示第t个窗口

2)for each ej in FI-i_List{

//ej表示在NCFP-Tree树中挖掘的临界频繁项集

3)Fej=Fej+num //num是临界频繁项集ej的支持度计数

4)else

5)creat ej

6)Fej=num}

3.频繁项集产生阶段

输入:滑动窗口中每个基本窗口的NCFP-Tree,最小支持度阈值min_sup,滑动窗口W的大小m

输出:完全频繁项集

1)按照临界频繁项头表的顺序取项目ei

2)for each ei in ID_List{

3)挖掘NCFP-Tree中所有包含ei的临界频繁项集,存在对应的FI-i_List中}

4)for each ei in FI-i_List{

5)if Fei>=min_sup

6)输出项集ei和它的支持度计数并存储在FI_List中;

7)else

8)输出ø

9)输出完全频繁项集FI_List}

3.4 MFI-SW算法的执行过程

以表1所示的事务数据流为例介绍算法的每步执行过程,设滑动窗口的大小为2(也就是说一个滑动窗口包含2个基本窗口),最小支持min_sup=0.4,ε=0.1.

表1 事务数据流
Table 1 Transaction data stream

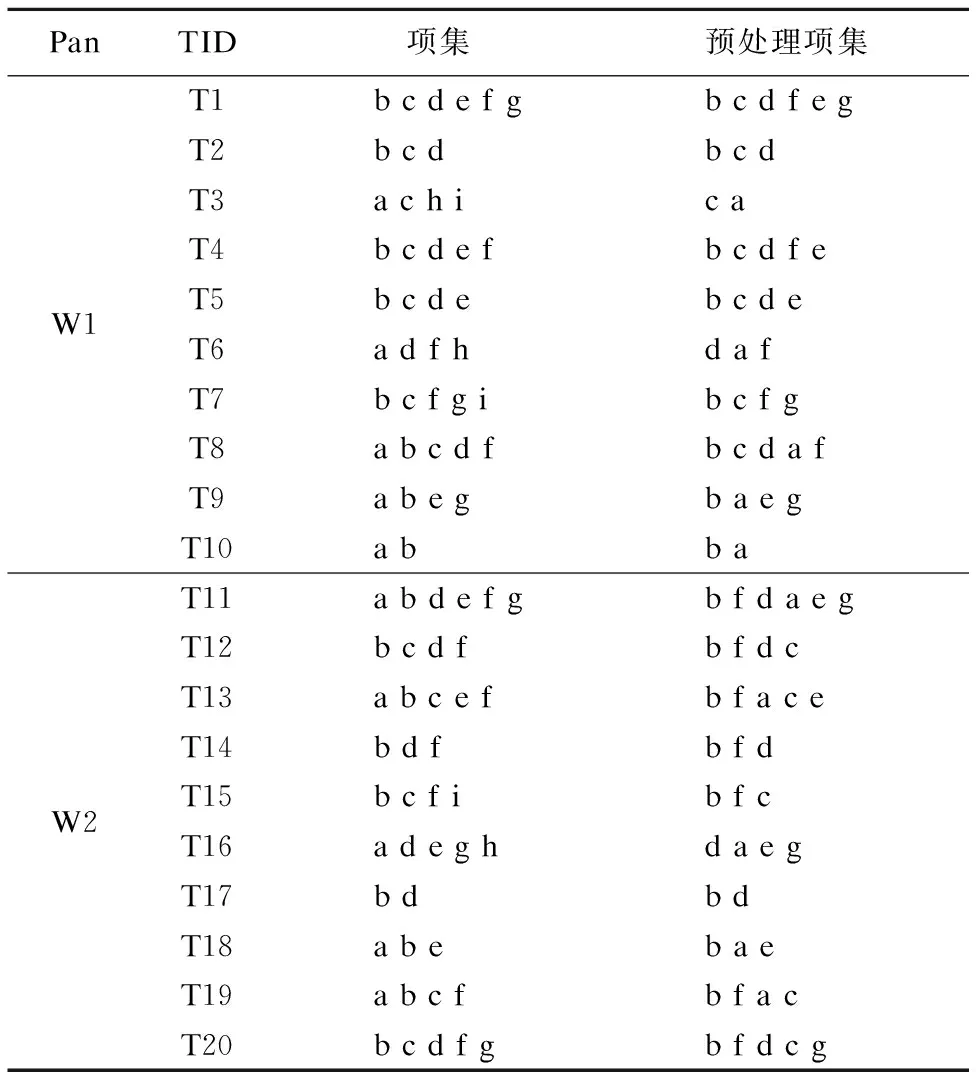
PanTID项集预处理项集W1T1 b c d e f gb c d f e gT2b c db c dT3a c h ic aT4b c d e fb c d f eT5b c d eb c d eT6a d f hd a fT7b c f g ib c f gT8a b c d fb c d a fT9a b e gb a e gT10a bb aW2T11a b d e f gb f d a e gT12b c d fb f d cT13a b c e fb f a c eT14b d fb f dT15b c f ib f cT16a d e g hd a e gT17b db dT18a b eb a eT19a b c fb f a cT20b c d f gb f d c g

1.窗口初始阶段

数据流流入滑动窗口时,以基本窗口为单位,首先建立第一个基本窗口对应的项目矩阵PM1,如表2所示,为了节省时间和空间,先把不频繁的h和i两项过滤掉.然后根据项目矩阵PM1对临界频繁项头表进行降序排列,即bcdafeg,进而将数据压缩存储在NCFP-Tree树中.

表2 项目矩阵PM1
Table 2 Project Matrix PM1

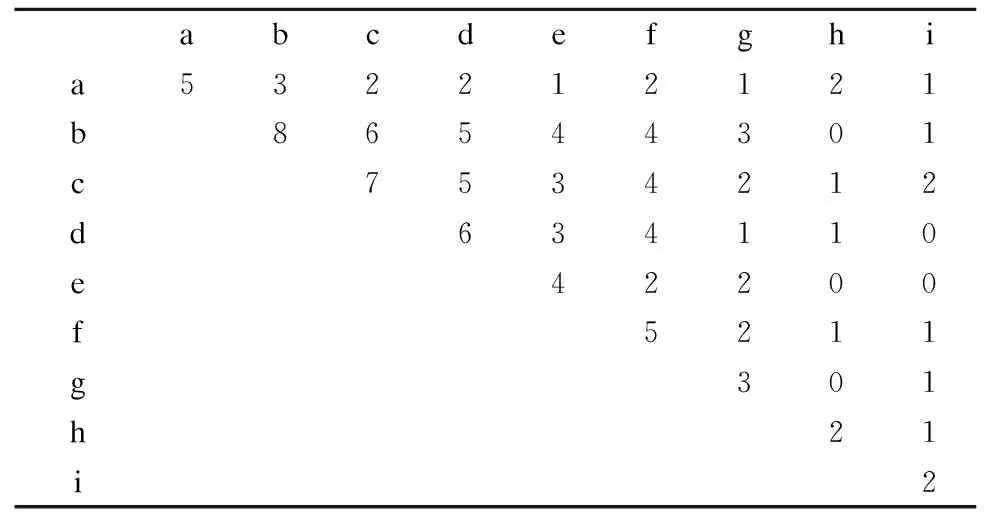
abcdefghia532212121b86544301c7534212d634110e42200f5211g301h21i2

扫描表1中预处理数据,建立对应的NCFP-Tree1,每插入一个节点,都要扫描项目矩阵PM1,查看该节点能否与祖先节点构成临界频繁2-项集,如果能,则该节点插入在该祖先的孩子节点上,如果没有,继续向根部搜索,假设到达根节点NULL都不能找到与该节点组成临界频繁2-项集的祖先节点,那么剪掉该结点.如图1所示是第一个基本窗口对应的NCFP-Tree1.

利用同样的方法,建立第二个基本窗口的项目矩阵PM2和它对应的NCFP-Tree2.

2.窗口滑动阶段

窗口滑动以后,采用最新的基本窗口的项目矩阵覆盖最旧的基本窗口对应的项目矩阵,释放最旧基本窗口对应的NCFP-Tree.同时用同样的方法建立最新的基本窗口对应的NCFP-Tree,频繁项集表FI-i_List也要随之更新,这里采用新基本窗口挖掘出来的频繁项集直接覆盖最旧的基本窗口挖掘的对应项集.

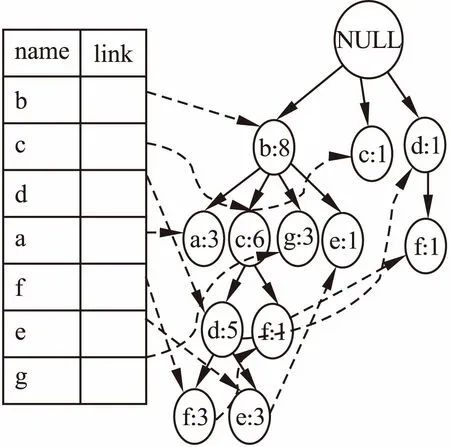
图1 第一个基本窗口的NCFP-Tree1Fig.1 First basic window NCFP-Tree1

3.频繁项集产生阶段

根据性质3可知,项目矩阵PM中包含频繁1-项集和频繁2项集的全部信息,因此可以通过扫描事务矩阵PM1得到临界频繁1-项集FI-1_List={a:5,b:8,c:7,d:6,e:4,f:5,g:3}和临界频繁2-项集FI-2_List={ab:3,bc:6,bd:5,be:4,bf:4,bg:3,cd:5,ce:3,cf:4,de:3,df:4},通过利用改进的挖掘临界频繁项集技术挖掘每个基本窗口对应的NCFP-Tree的所有临界频繁项集,得到FI-3_List={bce:3,bde:3,cde:3,bcf:4,bdf:3,cdf:3,bcd:5}和临界频繁4-项集FI-4_List={bcdf:3,bcde:3}.用同样的方法可以挖掘第二个基本窗口,可得临界频繁1-项集FI-1_List={a:5,b:9,c:5,d:6,e:4,f:7,g:3},临界频繁2-项集为FI-2_List={ab:4,ae:4,af:3,bc:5,bd:5,be:3,bf:7,cf:5,df:4,dg:3},临界频繁3-项集FI-3_List={bdf:4,abf:3,bcf:5},最终输出FI-i_List中的完全频繁项集的挖掘结果FI_List={a:10,b:17,c:12,d:12,e:8,f:12,bf:11,cf:8,df:8,bd:10,bc:11,bcf:9}.

4 MFI-SW算法分析

实验环境是操作系统为64位window7,3.20GHzCPU和安装内存是8.00GB,算法实现语言是C语言,实验数据流的数据集[15]采用的是IBM data generator生成的模拟数据.分别有稀疏集T7I4D100K,T10I4D100K和稠密集T40I10D100K,其中T表示的是事务的平均长度,I表示的是项集的平均最大长度,D表示的是总的事务项目.滑动窗口包含的基本窗口数为3,每个基本窗口包含10000条事务,设支持度为ζ,取允许误差因子ε固定为0.1ζ(ζ为最小支持度阈值).以下就算法的响应时间和查全率、查准率对MFI-SW算法和pWin算法、DSFPM算法进行实验对比分析.

4.1 算法响应时间

如图2所示,新算法MFI-SW和DSFPM算法和pWin算法在三种不同的数据集上的处理时间,最小支持度阈值为0.5%,实验结果标明MFI-SW算法随着平均长度的增加,时间消耗越大,在稠密数据集中的运行时间远高于稀疏集,主要是因为稠密数据集中的事务的平均长度和项集的平均最大长度比较长,在滑动窗口中,更新数据和挖掘频繁项集的过程比较消耗时间,所以该算法更合适稀疏数据集.

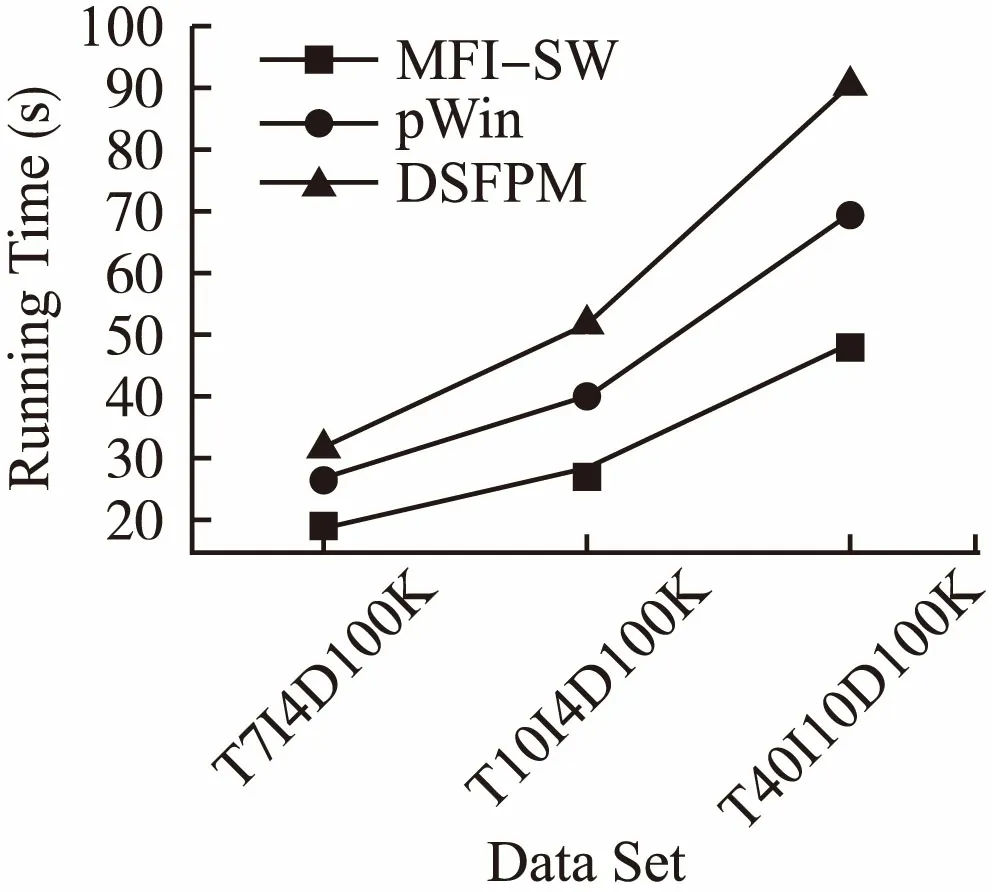
图2 不同数据集上的运行时间比较Fig.2 Runtime comparison on different datasets

如图3所示,在稀疏集T10I4D100K下对MFI-SW算法与DSFPM算法、pWin算法在不同最小支持度阈值下的处理时间进行了比较.实验结果表明在最小支持度阈值从0.5%到1%变化的过程中,三个算法的时间开销的变化趋势都是随着支持度阈值的增加,每个基本窗口挖掘出来的临界频繁项集数目减少,因此时间开销也随着减小,但是MFI-SW算法的时间性能略高于另外两个算法.

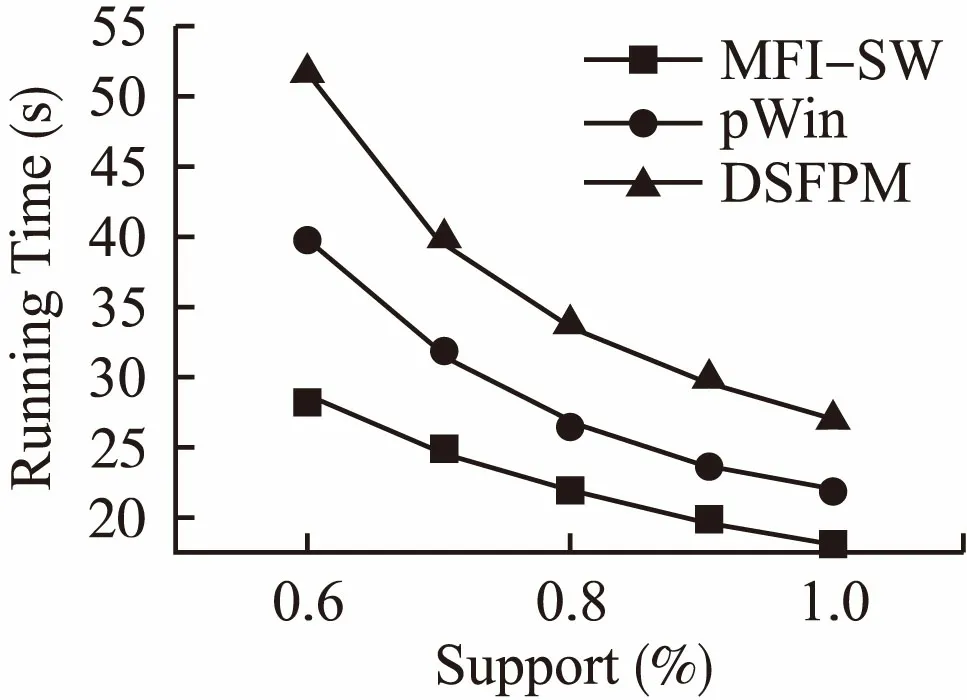
图3 不同支持度的运行时间比较Fig.3 Comparison of run time with different support

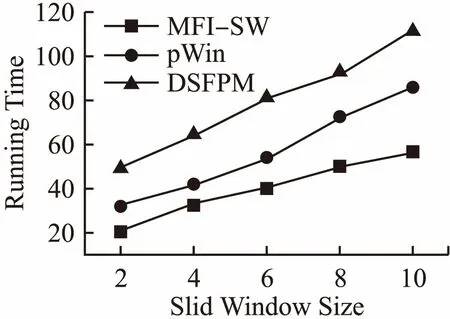
图4 不同的窗口大小、算法运行时间的比较Fig.4 Different window sizes、comparison of algorithm run time

如图4所示,为了显示窗口大小对所有算法的时间使用的影响,在稀疏集T10I4D1000K中测试不同窗口大小的情况下,MFI-SW算法与DSFPM算法、pWin算法的时间开销,取最小支持度阈值ζ=0.5%.实验结果表明滑动窗口越大,算法的时间开销越大,MFI-SW算法随着滑动窗口的增加,时间开销变化较稳定,其他两个算法pWin和DSFPM在滑动窗口增加的情况下,因为它们都需要频繁的更新树结构,所以时间开销变化较大.

4.2 算法的查准率和查全率

在算法中最大误差是一个非常重要的剪枝参数,查准率指的是算法挖掘出来的实际频繁项集的数量与算法挖掘出来的输出数量的百分比,而查全率则指的是算法挖掘出来的实际频繁项集的数量值与真实数量的百分比.一般情况下,在数据集中挖掘频繁项集以最大的误差值作为剪枝参数,在挖掘过程中更新树结构时对算法的查全率和查准率有很大的影响,图5和图6测试了IBM合成数据流中的前三条数据流[16]中不同误差值对算法的查准率和查全率的影响.假定误差值分别为0.0002,0.0008,0.0014和0.002时,观察测试结果.

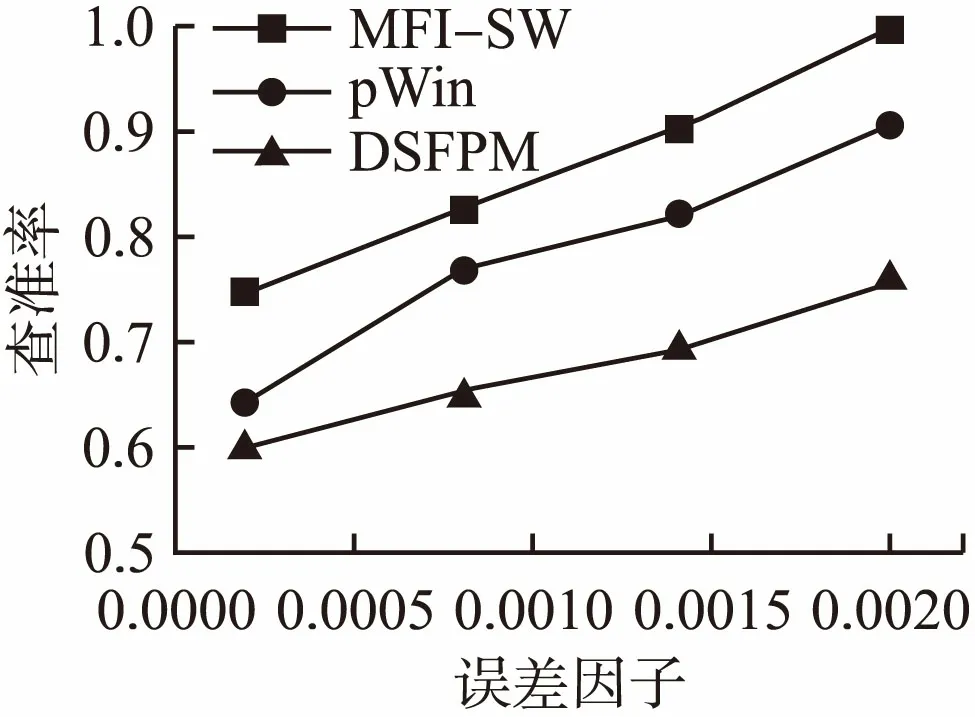
图5 不同的误差因子、算法查准率的比较Fig.5 Different error factors、comparison of algorithm precision

从图5和图6中不难看出,在误差值逐渐变大的过程中,MFI-SW算法的查准率和查全率高于pWin和DSFPM两个算法.因为当误差值逐渐增大的过程中,挖掘出来的频繁项集的数量变少,于是用户指定的误差值越大,挖掘出来的频繁项集数量就越少,挖掘多条数据流中的频繁项集的准确率和查全率就会越高.

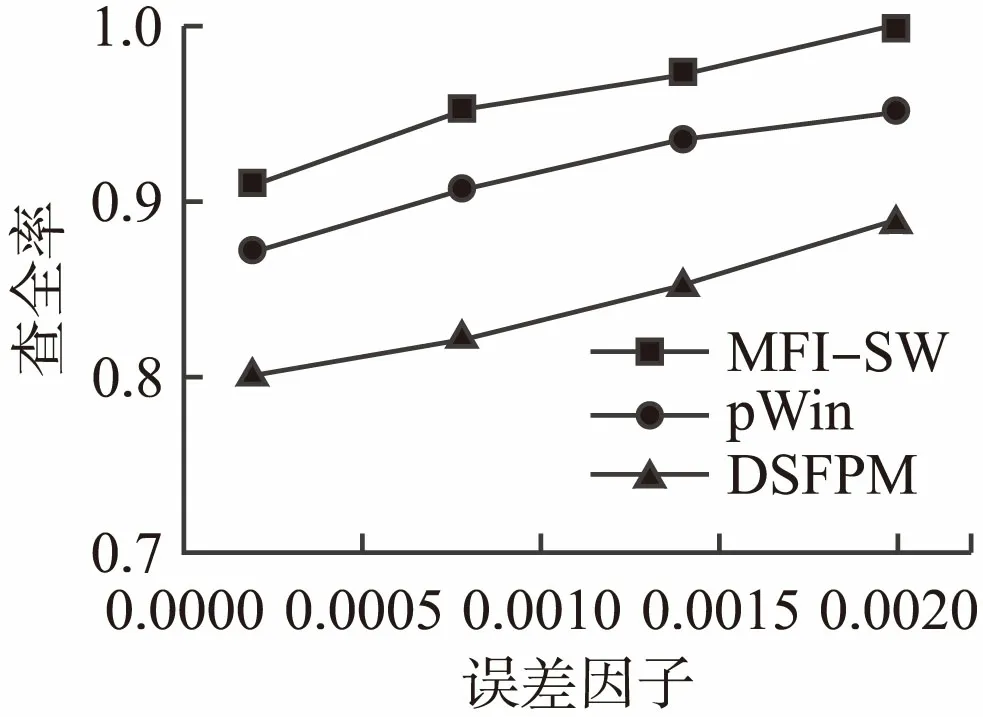
图6 不同的误差因子、算法查全率的比较Fig.6 Different error factors、comparison of algorithm recall rate

5 结束语

本文提出了滑动窗口中FP-Tree的频繁项集挖掘算法MFI-SW,该算法采用上三角矩阵的存储方式,每个基本窗口建立一个NCFP-Tree来压缩存储数据信息,在相同节点个数的情况下,NCFP-Tree较FP-Tree的深度低,分支少,因为NCFP-Tree中的父子节点保留临界频繁2-项集的全部信息,窗口滑动时,将旧基本窗口的NCFP-Tree释放,建立新基本窗口的NCFP-Tree,整个过程中保证每棵树都按基本窗口中的1-项集的支持度计数的降序排列,有效的提高了MFI-SW算法的压缩效率,并为频繁项集的输出带来方便,通过与经典的算法比较证明,MFI-SW算法具有良好的时间性能.在此基础上还需研究以二项集为根,建立树结构,这样使树结构更矮,挖掘效率更高.