生物特征信号提纯算法的设计与实现*

孙湘，华钢

(1.江苏大学附属医院信息科,江苏 镇江 212001;2.中国矿业大学信控学院，江苏 徐州 221116)

1 引 言

生物特征信号是观测各种生命体征的一个窗口，在生物科学研究、保健、疾病预防以及医疗仪器生产中具有重要意义[1]。对于常规方式获取的生物特征信号，多数掺杂着干扰信号，在一定程度上影响了对生物特征信号的检测与分析。一些外界高强度噪声淹没了有用的生物特征信号，使人们对有用的生物特征信号的提取分析变得非常困难。对采集的生物特征信号进行提纯处理是生物信号检测的基础[2]。高效的提取方法能帮助后期定量诊断和精确治疗[3]。

实际采集的生物特征信号多是随机噪声混杂的多分量时变信号，有效去除生物特征信号中的噪声，是实际应用中所面临的主要问题[4]。传统的去噪方法多是只在频域或时域内进行，但生物特征信号与噪声信号之间通常是以时频交叉形式存在的，使得现阶段的消噪方法难以实现信噪分离。以短时傅里叶变换[5]为代表的线性时频表示方法对随机噪声混杂的时变信号进行分析时，不会产生交叉项，但该方法时频分辨率不高。以WVD算法(Wigner-Ville分布)[6]为代表的非线性时频表示方法，具有较高的时频分辨率，但无法避免交叉项的产生。以Chirplet时频变换为代表的时频分解方法，将生物特征信号分解为不同的基函数，再根据基函数的Wigner-Ville分布来取代生物特征信号的时频分布，这样既能避免交叉干扰项的产生，也能提高信号时频分辨率。

综合分析上述理论，我们提出一种基于联合时频变换的生物特征信号噪声的抑制方法，对生物信号在时域和频域内进行特征分解，有效避免了交叉项的干扰，且能够获得较高的时频分辨率，并将该方法应用到生物特征信号提纯中。

2 方法的设计

2.1 生物特征信号提取与预处理

对生物特征信号分析的第一步，是信号采集和重建。对生物特征信号的有效采集是生物特征提取的基础，采集的生物信号输出状态表现为非线性平稳形式。通过对信号的采集和处理，将结果输入到专家系统进行判别。假设采集的生物特征信号x(t)为连续信号，生物特征信号的频域表达式为：

z(t)=x(t)+iy(t)=a(t)et

(1)

其中：

(2)

式中，a(t)和θ(t)分别用于描述解析信号的包络和幅值，满足时频联合分布，获得生物特征信号的解析表达式为z(t)，z(t)是x(t)与1/t的卷积形式，其中x(t)满足平移不变性，获得生物特征信号的非平稳特征形式为：

(3)

将生物特征信号在时域和频域内进行特征分解，得到信号x(t)的修正平滑伪WVD表达式为：

(4)

其中，x(τ)用于描述信号x(t)的修正平滑为WVD的特征尺度，f用于描述信号时频域调制频率，t表示时间，ui′j′和pci′分别表示为描述信号时的警告值和良好值。计算Cohen类的频谱[7]，获得生物特征信号x(t)输出能量的密度谱为：

SPEC(t,f)=(ui′j′+pci′)·x(t)

(5)

由于通过线性变换和正交性分解获得的生物特征信号存在噪声分量，需要对这些噪声分量进行滤波处理，设计了匹配滤波检测器，使用该检测器进行生物特征信号滤波。

Yk=[yk1,…,ykJ]

(6)

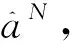
(7)

因此，选取匹配滤波系数β=0.085，生物特征信号采样长度取为3000，利用希尔伯特-黄变换方法进行生物特征信号频率分析。

2.2 基于联合时频分解的生物特征信号提纯

经过固有模态分解后一些噪声信号得到有效去除，生物特征信号分量的时频分布与垂直于时间轴频带宽的直线基本相同，在时域内易于识别。设定生物特征信号分量与其余分量在时频域内是不相交的，则可利用区域抽取算法获取生物特征信号分量。对生物特征信号根据WVD算法进行时频分解时，假设在时频域内，生物特征信号分量与剩余信号分量是相交的，提取生物特征信号时频区域的具体步骤如下：

(1)假设生物特征信号分量先分解出，则直接利用加立体窗函数提取分量的时频分布，即：

Px(t,f)=P(x,y)Mx(t,f)

(8)

其中，P(x,y)表示提取的生物特征信号原时频分布，Px(t,f)表示希望获取的信号时频分布，Mx(t,f)表示掩膜函数。

(2)假设，与特征分量时频交叉的信号分量先被分解出来时，利用加时频窗方法[9]提取交叉分量的时频分布，即：

Py(t,f)=P′(t,f)My(t,f)

(9)

(3)其中，P′(t,f)表示交叉分量先获得时的时频分布，My(t,f)表示交叉分量先获得时的掩膜函数，Py(t,f)表示与信号分量在时频域内交叉分量的时频分布。采用下式提取交叉分量与信号分量的混合时频分布：

Pxy(t,f)=P″(x,y)Mxy(t,f)

(10)

(4)其中，P″(x,y)表示交叉分量和特征分量均得到时的时频分布情况，Mxy(t,f)表示交叉分量和特征分量均得到时的掩膜函数，Pxy(t,f)表示交叉分量和特征分量的混合时频分布。采用式(11)获取生物特征信号的时频分布：

Px(t,f)=Pxy(t,f)-Py(t,f)

(11)

(5)生物特征信号时频域内，一维时频分布与二维时频分布不是直接的映射关系，对生物特征信号进行重构，需要找到一种信号模型，根据该模型使其时频分布根据最小均方差准则[10]去逼近期望的时频分布Px(t,f)，信号模型表示如下：

hn(t)=knexp(-pn(t-un))sin(2πfn(t-un))

(12)

(6)对式(12)中的hn(t)进行Wigner-Ville分布变换，将WVD-WVDhn(t,f)根据下式逼近Px(t,f)，即：

H=min∬E|WVDhn(t,f)-Px(t,f)|2

(13)

由上式逼近求解获得的hn(t)可看作是Px(t,f)相应特征信号。通过对时频信号逼近所得到的hn(t)进行线性叠加，即所需提纯的生物特征信号。

3 实验数据与平台

实验在Intel(R)Pentium(R)4，CPU 2.30 GHz，内存2 GB，操作系统Microsoft Windows7(64-bit)上进行，以某设备采集的生物特征信号样本为研究对象，对其进行滤波仿真。生物特征包括指纹,虹膜,人脸等, 心电信号具有准确性，更高实时性，易被识别的特征性。本研究以心电信号(electrocardiogram,ECG)的生物识别技术为例，通过WVD获取生物特征信号的有用信息，获得其WVD变换频谱图。

仿真过程中，设定参数f1=0.2，f2=0.3。其中，f1表示生物特征信号归一化初始频率，f2表示生物特征信号终止频率。在噪声干扰下，生物特征信号与噪声的信噪比SNR=-10 dB。对生物特征信号进行上述算法处理获得的2组心电信号样本的提纯结果见图1。

(a)

(b)图1 心电信号提纯结果(a).心电信号检测样本1；(b).心电信号检测样本2Fig 1 ECG purification results (a).ECGsignal detection sample 1； (b).ECG signal detection sample 2

分析图1可知，所设计的提纯算法滤波效果良好，有效去除了大量的噪声，保留了生物特征信号的有效成分，为后续的频谱检测所用。

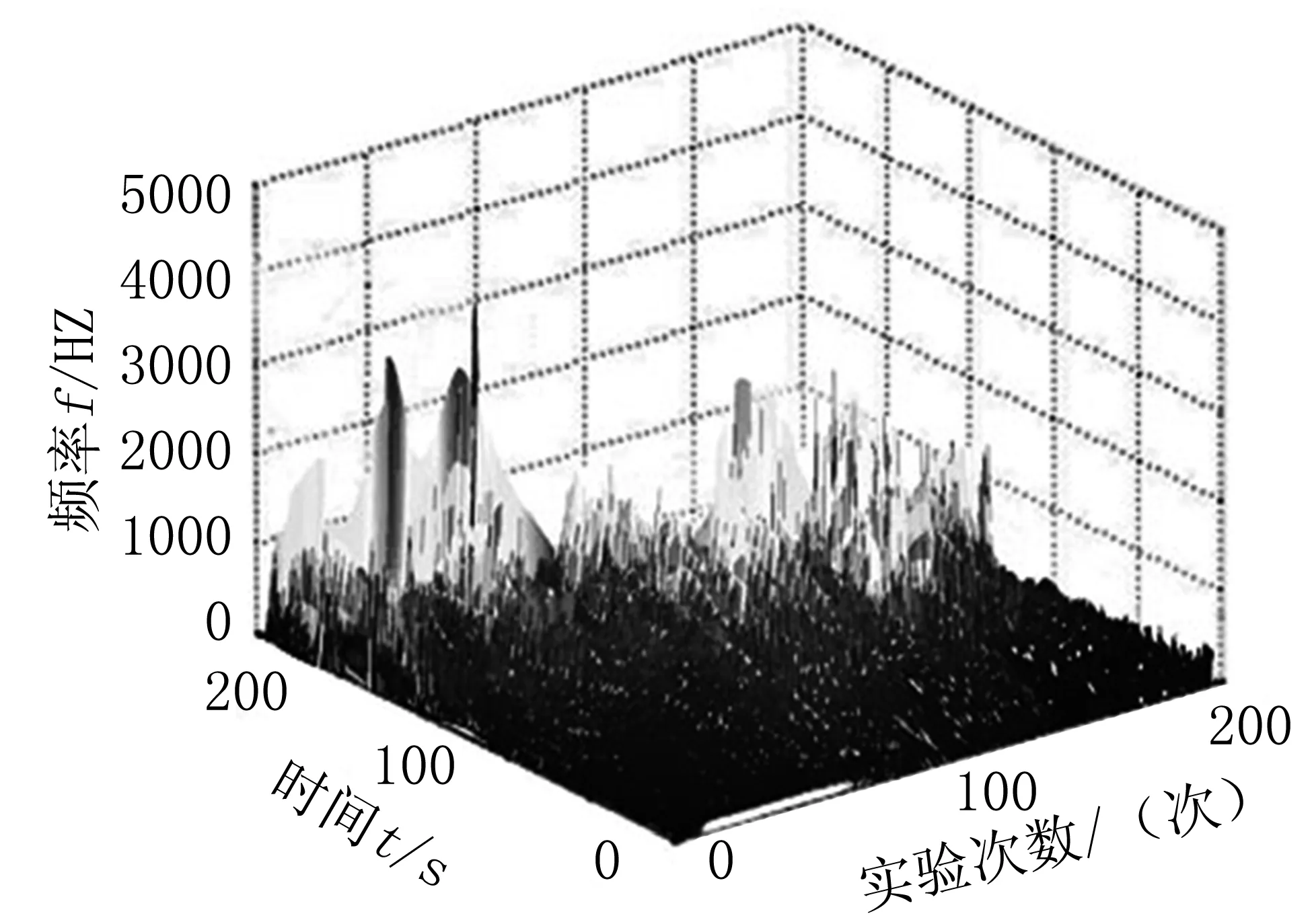
对于其中的一组心电信号样本，分别采用WVD算法、Chirplet分解法、短时傅里叶变换联合的变换检测算法和传统的WVD检测算法获得的心电信号检测频谱图见图2，其中SNR=-10 dB。

由图2可知，实际采集的心电信号中含有一些噪声信号，产生了大量的干扰信息。经过所设计的信号提纯算法处理后，获得的WVD图中脊线清晰可见，中间区域能量聚集明显，说明心电信号特征时频聚集性较高，可在图2(b)中看到有一个明显的心电信号存在。而传统的WVD检测算法欠佳，出现大量的伪峰，见图2(a)，难以有效检测和提取生物特征。

(a)

(b)图2 心电信号检测频谱结果(a).传统的WVD检测；(b).联合变换检测Fig 2 Spectrum results of ECG signal detection (a).Traditional WVD detection； (b).Joint transformation detection

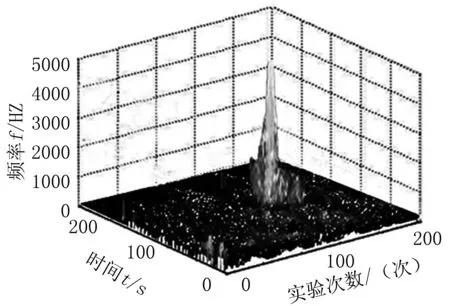
采用Monte Carlo实验，计算传统WVD检测算法和联合变换检测算法的检测概率(%)，计算结果见表1。

表1 不同检测算法的检测性能对比

在SNR=-10 dB下，实验次数为100次时，传统的WVD检测算法的检测概率为89.7%，所设计的算法检测概率为98.2%，与传统的WVD检测算法相比提高了8.5%。仿真实验结果表明，所设计的信号提纯算法可以有效地进行信号分析提纯，生物特征信号检测结果可为后续医疗诊断奠定基础。

4 结论

结合联合时频分解方法提出了生物特征信号提纯方法。研究可知，通过本研究提出的改进方法，可以提高图像处理的信噪比，有效去除了大量的噪声，保留了生物特征信号的有效成分，采用设计的提纯算法进行生物信号特征提取，能够有效分析生物信号的频率信息，对于非平稳生物特征信号的噪声抑制具有明显的优越性。需要指出的是，所设计的提纯算法运算量较大，需要进一步的优化。