基于Field II的非衍射阵列波声场的仿真研究*

刘冬雪，彭虎，韩志会

(合肥工业大学，合肥 230000)

1 引 言

常用的非衍射声场有Bessel声场，X_wave声场，阵列波声场等[1]。Bessel声场是连续波声场，X_wave声场激励信号是复数且能量集中在z轴附近很难实现波束偏转，难以应用到实际中。卢建宇教授提出了阵列波，这种波束可以用于高帧率超声成像。其中分层阵列波的声场分布与纵坐标无关，因为波束形状像分层的栅栏而得名[2]。声场在传播过程中无法抑制噪声的干扰导致成像效果不够理想，因此，研究如何使声场保持非衍射特性传播更远为非衍射波应用于实际提供了理论支持。

波动场常用积分衍射公式法进行仿真，但是这种方法计算量大，精度低[3]。为了提高效率，本研究使用超声领域中常用的仿真软件Field II进行仿真研究。为了使声场传播更远，一般采用幅度变迹技术进行加权，通常使用三角函数作为加权函数。常见的有Hanning窗、Hamming窗、布莱克曼窗、余弦窗等，加权值是从阵元中间向阵元两侧缓慢变小的。通过幅度变迹技术可以增加成像的分辨率，这种方法虽然抑制了旁瓣，但是却加宽了主瓣，空间分辨率也下降了。究其原因是幅度变迹都在发射声场以前进行设置，这种设置是固定的，与声场本身是没有关系的[4-6]。因此，人们提出了自适应波束形成的方式进行加权，该方法是根据接收声场信号计算最优权并对接收信号进行加权，从而抑制噪声获取更高的成像分辨率[7]。

本研究通过对Capon波束形成算法的研究提出一种适用于发射声场的Capon窗加权方式，并结合幅度变迹技术，使阵列波在更大的范围内保持非衍射特性。

2 理论介绍

2.1 阵列波理论

阵列波是非衍射波的一种，基于一般标量波动方程推导而来[8]。一般N阶齐次标量波动方程见式(1)，其中xi(j=1，2，…，N)代表N维空间直角坐标，t代表时间，N是大于0的整数，c是声速，Φ(x1，x2，……，xN；t)=f(s)是N维声场函数。

(1)

令N=2，x1=x，x2=z解得，

ΦL(x，z-c1t)=(cosKxx)eiKz(z-c1t)

(2)

2.2 Capon算法应用到发射声场

标准Capon算法(standard capon beamformer，SCB)也称之为最小方差无畸变响应，其基本目的是寻找到最佳加权向量W=[W1，W2，…，WN]，在保证期望方向θ增益最大的条件下，使干扰信号和噪声信号的输出功率最小[9]。Capon算法一般用于接收声场的处理，本研究用于发射声场，因此假设Capon算法处理的声场是某深度下传感器接收到的信号。见图1，仿照产生分层阵列波的发射传感器，假设某深度zt有N个线性传感器阵列组成的二维传感器进行发射声场接收。每个线性传感器有M个阵元。因此本研究某时刻下发射声场系统的功率可表达为：

(3)

图1 阵列波传播空间示意图Fig 1 The diagram of layered array beams propagation

式(3)中，

(4)

设Φxx为深度zt下矩形传感器上接收信号X(n)的自协方差。

Capon算法的代价函数[7]为minW*ΦxxWsubjecttoW*a(θ)=1，a(θ)表示指向方向θ的方向向量，W*表示加权向量共轭转置。上式可以通过拉格朗日因子的方法求解，将这个问题转化为无约束最优化问题：

L(w)=w*Φxxw+λ(w*a(θ)-1)

(5)

式中λ是拉格朗日因子。至此就可以求出加权向量W的值。

(6)

利用延时叠加法中的延时处理，将方向向量表示为a=[1，1，…，1]T，T表示矩阵转置[11-12]。

2.3 复合权加权方式

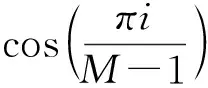
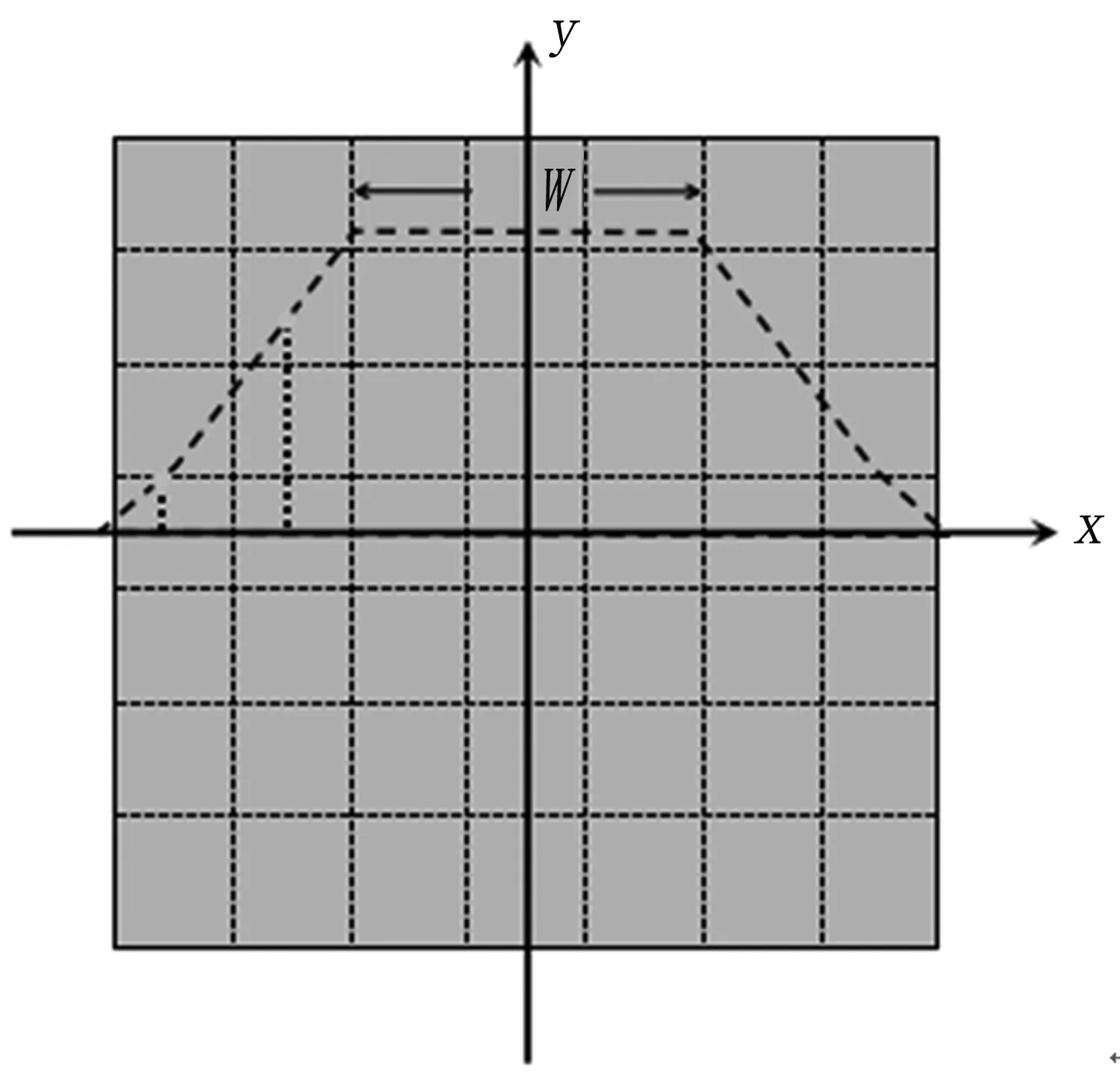
图2 传感器复合权加权方式Fig 2 The composite weighting method of transducer

3 Field II真

3.1 Field II仿真函数

对声场仿真主要使用以下函数：

(1)xdc_2d_array()，该函数功能是建模2d传感器[13]。xdc_2d_array()函数中特殊参数enabled表示阵元是否采用，1代表有效阵元，0代表无效未被选用阵元[14]。可用该函数设计同心圆环传感器。

(2)xdc_get()，该函数功能是获取传感器上每个阵元的物理信息。xdc_get()函数会获得26行、物理阵元总数列大小的矩阵，每一行表示的是物理阵元的实际信息。

(3)ele_waveform()，该函数的功能是对每个阵元逐一激励。由于仿真分层阵列波不同横坐标激励信号不同，可以使用该函数对每个阵元逐一激励[15]。

(4)calc_hp()，该函数功能是计算空间中各位置声场的强度。calc_hp()函数逐点对空间点进行声场计算，每点返回值分别为“hp”、“start_time”，其中start_time为起始采样时刻，hp为从采样时刻开始以采样间隔1/fs采样到的所有声场信号。因为各点采样时刻不同，需做时间对齐才可得到该时刻下声场分布。

本研究使用150×150个阵元的传感器，阵元高、宽均为0.2 mm，阵元x、y方向间隔均为0.1 mm，声速1 540 m/s，采样频率100 MHz，传感器脉冲响应为中心频率f0=2.5 MHz、脉冲宽度2个周期的正弦信号。

3.2 加权仿真研究

由上图可见分层阵列波声场有清晰的6条明亮竖条纹波束，分层阵列波类似于平面波的传播方式，波束以图中形状在x-y平面沿z轴向前传播[2]。图中加了噪声的声场尾影明显，中间声场部分也受到了噪声影响。在实际应用中声场传播过程无法避免噪声的干扰，为了使阵列波保持非衍射特性传播更远是将阵列波声场应用于实际非常重要的一个待解决问题。

本研究通过Field II分别进行了幅度变迹、单一Capon窗加权、复合窗加权的声场仿真，讨论加各种权值对含高斯白噪声的声场产生的效果见图4。

图3分层阵列波近场区声场分布

Fig3Thenearfielddistributionofthelayeredarraybeams

图4 含噪声场不同加权方式仿真结果Fig 4 The simulation results of different weighted methods of noise field

通过观察上图的仿真结果可知，含有噪声的声场在z=150 mm时波束已经完全发散，波束受噪声干扰严重已经看不到明显的分层形状。使用余弦权进行加权可见在该深度下声场有分层形状，该方式对噪声有一定的抑制作用。z=150 mm时加Capon窗的声场和加复合权的声场效果相近都有很好的非衍射特性，因此，在近场区域可以使用Capon算法代替复合权进行激励。对于声束沿y轴方向尾影的抑制，加复合权方式比加单一的Capon窗效果好。复合权方式有效的抑制噪声的同时减少了声场边缘旁瓣幅度，使声场能量更集中从而可以保持良好的非衍射特性，因此可以传播的更远。在一些工业检测以及医学中较厚组织器官的检查要求更深的声场传播范围，此时可以使用复合权对阵列波进行加权处理。

4 结论

本研究基于Capon算法提出一种适用于发射声场的Capon窗加权方法，并使用FieldII仿真分析各种加权方式对含噪声场的作用效果。通过仿真结果得知，使用本研究提出的Capon算法比余弦窗更好的保持了非衍射波的非衍射特性。单一Capon窗仿真的声场边缘开始发散，复合权方法抑制噪声的同时也对边缘发散声场进行了有效抑制。本研究进行了理论探索研究，通过仿真验证了该方法的可行性，在实际应用中可以通过计算机模拟实际介质参数，并通过本研究仿真方法获得发射声场信号计算Cpaon权值。也可以使用水听器直接获取任意空间位置发射声场信号。

该方法具有如下特点：(1)使用超声领域内常用的仿真工具Field II进行仿真研究，仿真结果更可靠，相比传统的计算仿真可以避免计算过程产生的误差。软件仿真能够更快速便捷的进行参数调试，节省了成本，为应用研发提供了理论依据。(2)本研究基于Field II开发出一套声场仿真系统，该系统可以实现任意声场仿真，并显示声场任意时刻任意平面波形灰度图。(3)在实际应用中只有有限孔径的传感器，激励在传感器边界会骤减为零，一些频率不连续点附近会引起较大误差，为了避免这种误差的产生，本研究基于Capon波束形成提出复合窗算法，传感器中间范围采用本研究提出的Capon窗加权激励，边缘采用余弦窗加权激励，使其谱函数的主瓣包含更多能量，相应旁瓣幅度更小。通过仿真结果可知加复合权激励能够使非衍射波保持非衍射特性传播更远。