不同张口位移速率下带裂缝混凝土轴拉试验研究

胡钰泉，胡少伟,，黄逸群，明 攀

(1.河海大学 力学与材料学院，南京 210098；2.南京水利科学研究院 材料结构研究所，南京 210024)

混凝土作为典型的速率敏感性材料，在承受静态荷载和动态荷载作用下所表现的力学特性有较大差异，且混凝土广泛应用于各类建筑工程中，不可避免地会承受冲击、地震、爆炸等动态荷载的作用，因此，研究混凝土在动态荷载作用下的力学性能有重要的价值。

由于混凝土在建筑结构中主要承受压力，关于混凝土的速率相关性研究，早期研究者大多集中于混凝土的受压方面的研究，并取得了丰硕的成果[1-3]。但是对于混凝土材料，裂缝的出现以及结构的破坏往往是由抗拉能力不足导致的。因此，关于混凝土受拉动力性能研究得到学者广泛的关注[4-7]。肖诗云等[8]对普通混凝土受拉试件在应变率10-5～10-1s-1内进行动态单轴直接拉伸试验，研究表明混凝土的弹性模量和泊松比随应变速率的增加变化不大，混凝土的抗拉强度、临界应变与应变率之间呈线性关系，并给出了抗拉强度、临界应变受应变率影响的经验公式。范向前等[9]分析了七种不同应变速率条件下的混凝土应力-应变曲线、轴向拉伸强度及变形特征，得出弹性模量随应变速率呈线性增长的规律。但是由于试验方法，试验机的控制效果以及混凝土本身的离散性导致不同研究者所得的结论相差较大，甚至相互矛盾。因此，需要继续开展混凝土动态轴向拉伸的试验，研究混凝土动态轴向拉伸的力学性能。

为拓展混凝土轴向拉伸力学性能研究，提高轴向拉伸试验的成功率，试验采用自制的夹具，预制中间贯穿裂缝，控制裂缝处于试件中心位置，裂缝不发生倾斜，保证为I型裂缝，具体试件样式及预制缝制作见图1。优点之一是可以保证试件在直拉段破坏，可以进行混凝土断裂韧度等断裂力学性能分析，同时可以采用张口位移速率(即张口位移计每秒增加的位移长度除以张口位移的标距)控制，实现带裂缝混凝土的动态轴向拉伸试验。

1 试验概况

1.1 试件制备

采用试件形式为《水工混凝土试验规程》[10](DL/T 5150—2001)中的混凝土轴向拉伸C型试件，采用自制夹具，将预制钢板固定在模具中间位置，后浇筑混凝土成型为含有长30 mm，厚度为1 mm的中间贯穿裂缝的试件，试件尺寸及预制缝制作方法如图1所示。设计四组相同的试件，采用钢模浇筑，振动棒振捣，室内覆盖透水棉布养护28 d成型，自然放置60 d后进行试验。

所有试件强度等级均为C25，水泥采用南京生产的海螺牌复合硅酸盐水泥P.C32.5R，粗骨料连续粒级颗粒级配碎石(最大直径≤20 mm)，细骨料采用天然河砂(最大粒径≤5 mm)，配合比为水∶水泥∶砂∶石子=0.44∶1∶1.225∶2.485，浇筑24 h后拆模。

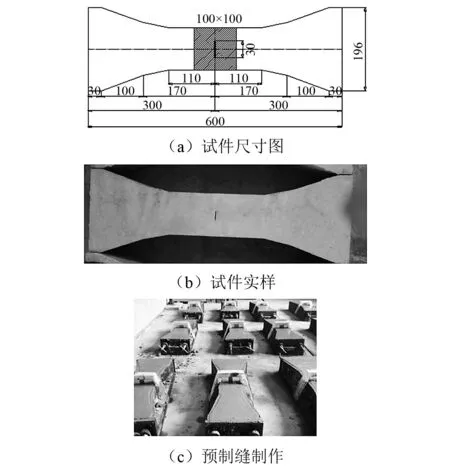
图1 试件尺寸及预制缝位置(单位：mm)Fig.1 Specimen size and crack location (unit:mm)

1.2 试验设备及加载方案

试验在1 000 kN微机控制电液伺服低周疲劳试验机上进行，压力传感器量程为30 kN。为精确测量高速率下混凝土P-CMOD曲线(即荷载-张口位移曲线。P为试验机所施加的外力荷载；CMOD为张口位移，即中间预制裂缝受荷载作用上下表面的相对位移)，采用长春机械科学研究院生产的张口位移计测量张口位移，其标距为12 mm，测量范围为0～2 mm，张口位移计的安装位置及测试位置如图2(b)，试验时直接将张口位移计接入疲劳机，与荷载同步采集。

在正式加载前，将试件置于试验机夹具中间，为减小偏心影响，用钢尺测量进行几何对中，采用力控加载至1 kN后，停滞10 s，等待张口位移计数值稳定，并检查试件是否仍然对中，若有偏移，则卸载重新安装，直至试件预加载后试件居中方可开始正式加载。待张口位移计数值及试验机油压完全稳定后转为采用张口位移计读数控制，控制张口位移速率在10-5～10-2s-1，加载大小通过张口位移计反馈信号到控制系统进行控制。采集设备与加载设备见图2(a)、图2(c)。

图2 试验设备及张口位移计图Fig.2Figure of test equipment and open mouth displacement meter

2 结果分析

2.1 断面特征

试验过程中绝大部分试件均从预制裂缝截面处断裂，不同张口位移速率下，断裂面均有粗骨料被拉断现象，如图3所示。随着张口位移速率的增加，试件断面越发光滑，且粗骨料断裂数目比例也逐渐增加，尤其对于10-2s-1的张口位移速率，断裂面粗骨料全部被拉断，断裂面非常平整。这主要是由于，在较低的张口位移速率下，混凝土拉伸破坏需要更多的时间来完成，混凝土起裂后，裂缝有足够多的时间沿着薄弱面扩展，而混凝土薄弱面一般为骨料与砂浆的结合面，少数含有缺陷的粗骨料被拉断，因此，张口位移速率越低，粗骨料被拉断数目越小，且断面越粗糙不平。相反的，在较高的张口位移速率下，所受荷载增加较快，能量积聚速度迅速导致裂缝扩展过快，来不及绕开骨料，直接将骨料拉断，从而造成断裂面骨料被拉断数目比例增加，断面趋于平整光滑。

图3 不同张口位移速率下的混凝土断裂截面图Fig.3 Fracture cross section of concrete under different opening displacement rates

2.2 荷载-张口位移曲线

在进行混凝土动态轴向拉伸试验时，混凝土试件在很短的时间内就发生了破坏，由于试验机本身刚度不足和油压控制不够稳定等因素，导致本试验的下降段数据采集的不够理想，因此，图4仅给出了四种不同张口位移速率下的P-CMOD曲线的上升段。

从图4可以得出，在试验受力之初，P-CMOD曲线基本表现为线性，随着荷载的上升，荷载增加缓慢，张口位移增加较快，进入非线性发展阶段，且张口位移速率越小，进入非线性的变化越明显。但由于混凝土本身的预制缝的存在，导致有效承载面减小，混凝土断裂过程区较小，从而混凝土一旦起裂就迅速失稳破坏，难以采集到混凝土的下降段。

此外，图4 (a)、图4(d)两条曲线有明显的卸载再加载现象，这是由于混凝土受力时，内部微孔洞，微裂缝等天然缺陷或主裂缝发展过程中，在遇到较大的缺陷时，导致混凝土的张口位移瞬时速率会迅速增加，而本身试验加载的方式是控制张口位移速率恒定，因此为保持张口位移速率恒定，试验机本身需要通过卸载来完成，造成出现卸载再加载的情况。试验过程中得到部分试件在下降段有卸载再加载的情况。因此，在试验机刚度较大，油压较稳的情况下，采用张口位移速率控制加载方式，易于得到混凝土轴向拉伸的加卸载曲线，从而得到轴向拉伸断裂试验的P-CMOD全曲线。

图4 不同张口位移速率下的P-CMOD曲线Fig.4 P-CMOD curves at different opening displacement rates

2.3 轴向拉伸强度与断裂韧度

通过试验数据的分析，将不同张口位移速率下的轴向拉伸强度列于表1。

从表1可以看出，混凝土轴向拉伸强度随着张口位移速率的增加明显提高，这主要是由于张口位移速率越高，荷载提升速度越快，混凝土内部裂纹产生和发展的时间越短，导致试件破坏时，内部裂纹来不及通过粗骨料与砂浆结合部位的薄弱面逐步开裂扩展，而直接通过粗骨料。以10-5s-1为准静态作用，当张口位移速率为10-4s-1，10-3s-1，10-2s-1时，动态轴向拉伸强度分别提高了9.8%，34%，60%。相较于文献[8-9]无缝混凝土在不同应变速率下的强度提升幅度较大，但趋势基本一致，如图5所示。这主要是本文试件中间有预制贯穿裂缝，由于预制裂缝的存在限定了裂缝起裂的位置与扩展方向，裂缝尖端存在应力集中，导致裂缝的发展与扩展时间进一步缩短，在试件破坏时，更多的骨料被拉断，张口位移速率越高，骨料破坏越多，粗骨料所承受的荷载越多，进而混凝土强度增强较多，曲线的斜率更大。

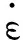
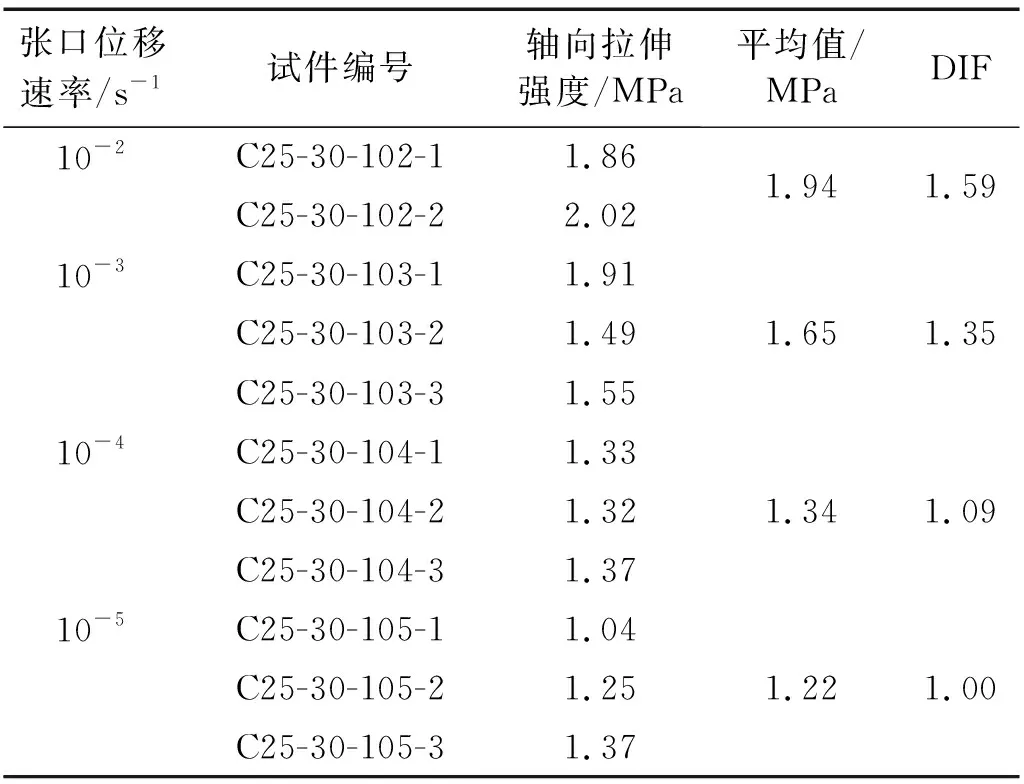
表1 不同张口位移速率下轴向拉伸强度值及其增长因子Tab.1 Tensile strength and its growth coefficient at different opening displacement rates

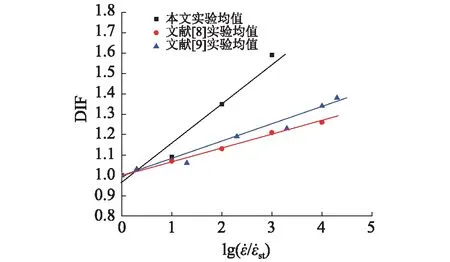
图5 混凝土轴向拉伸强度增加因子与张口位移速率关系Fig.5 Relation between increasing factor of concrete axial tensile strength and opening displacement rate

通过线性回归，得出本文混凝土动态抗拉强度增长因子与张口位移速率比之间的拟合计算式为

R2=0.947 8

(1)

混凝土的动态抗拉强度增长因子与张口位移速率比值的对数呈线性关系，这一结果与文献[11-12]研究成果相吻合。

由断裂力学知识可知，应力强度因子K反映裂纹尖端弹性应力场的强弱，裂纹失稳扩展的临界状态所对应的应力强度因子Kc即为断裂韧度。从上文可知，混凝土断裂过程区过小，导致混凝土一经起裂就失稳破坏，观察不到裂纹的扩展过程。根据文献[13]，中间带裂缝轴向拉伸试件应力强度因子按式(2)和式(3)计算

(2)

(3)

式中:σ为应力，MPa ；a为裂缝长度的1/2，mm；b为试件宽度的1/2，mm；F为几何因子，和裂缝的几何形状、试样形式、尺寸及加载方式有关。

以张口位移速率为10-5s-1的混凝土断裂韧度为准静态断裂韧度，定义高张口位移速率下的断裂韧度与准静态断裂韧度的比值αKC为动态断裂韧度增长因子，αKC与张口位移速率之间的关系如图6所示。由图6可知混凝土的断裂韧度随张口位移速率的增加不断增大，这一结论与文献[14]一致。根据式(2)和式(3)，断裂韧度与应力成正比，因此，通过线性回归，得出混凝土断裂韧度增长因子与张口位移速率比之间的拟合计算式与轴向拉强度与张口位移速率的计算式系数相同，结果如式(4)

(4)

R2=0.947 8

图6 混凝土动态断裂韧度增长因子与张口位移速率关系Fig.6 Relation between growth factor of dynamic fracture toughness of concrete and displacement rate of mouth opening

2.4 变形特性

2.4.1 弹性模量

对于带裂缝混凝土，弹性模量计算采用Tada应力强度因子手册[15]给出的荷载-张口位移关系式(5)

(5)

(6)

式中：V1为几何因子，和裂缝的几何形状、试样形式、尺寸及加载方式有关。

通过轴向拉伸试验测出混凝土P-CMOD曲线，通过对线性部分拟合，得到的值，代入式(5)计算得到弹性模量E。以10-5s-1的混凝土弹性模量为准静态弹性模量，定义高张口位移速率下的弹性模量与准静态弹性模量的比值αE为动态弹性模量增长因子，αE与张口位移速率之间的关系，如图7所示。

通过线性回归，得出本文混凝土动态弹性模量增长因子与张口位移速率比之间的拟合计算式为

R2=0.995 6

(7)

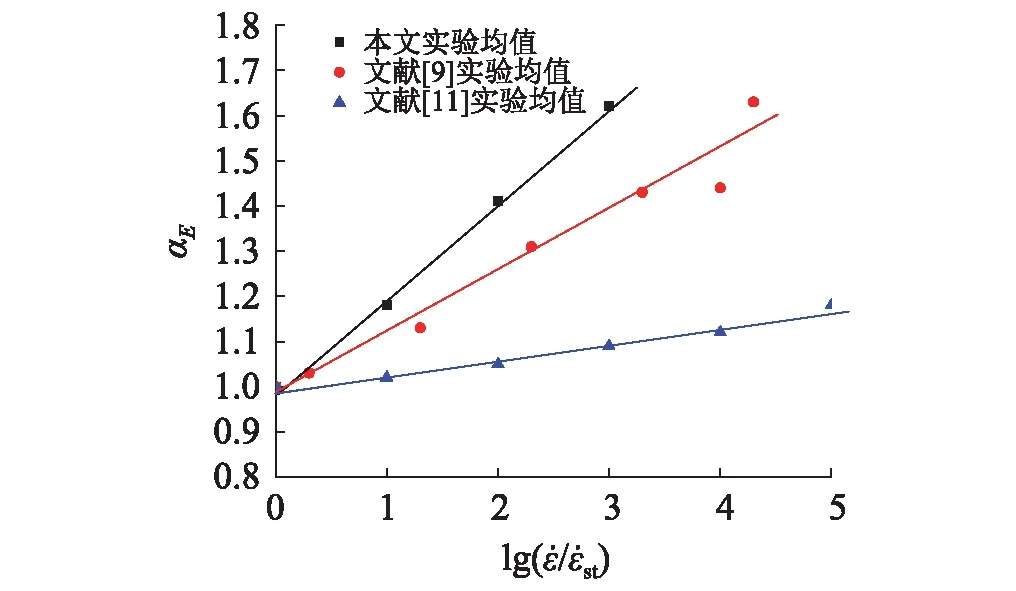
图7 混凝土动态弹性模量增长因子与张口位移速率关系Fig.7 Relation between growth factor of dynamic modulus of elasticity and opening displacement rate of concrete

由图7可知，随着张口位移速率的提高，混凝土的弹性模量均表现出逐渐增加的规律，以10-5s-1的混凝土弹性模量为准静态弹性模量，当张口位移速率为10-4s-1，10-3s-1，10-2s-1时，C25混凝土的弹性模量分别增加了17%，40%，61%，相较于文献[9]和文献[11]，弹性模量提升的速度更快。这主要是由于，随着张口位移速率的提高，导致混凝土断裂破坏时断裂面弹性模量较高的粗骨料破坏比例增加，在一定意义上贡献了混凝土整体弹性模量。而预制裂缝尖端导致的应力集中，造成混凝土更偏向于脆性破坏，变形减小，因此弹性模量增幅更大。

2.4.2 临界位移

临界位移为混凝土P-CMOD曲线上升段达到的荷载最大值时对应的张口位移，影响临界位移的因素有很多，水灰比，骨料类型，养护条件，加载条件等，本文采用控制变量法，研究张口位移速率的影响。表2给出了不同张口位移速率下临界位移值，通过对各组数据取平均值，得出图8的临界位移与张口位移速率的关系图，由图可知，四组试验所测的CMOD值在0.02 mm上下波动，说明带裂缝混凝土在达到荷载峰值，发生失稳破坏时的张口位移大小不随张口位移速率的增加而变化，与张口位移速率无关，表现为与混凝土材料本身性质有关的不变量。

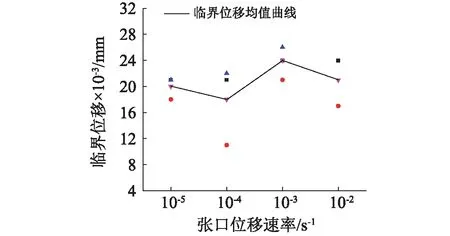
图8 临界位移与张口位移速率的关系Fig.8 The relation between the critical displacement and the opening displacement rate表2 不同张口位移速率下临界位移Tab.2 Critical displacement at different opening displacement rates

张口位移速率/s-1试件编号临界位移/mm平均值/mm10-2C25-30-102-10.024C25-30-102-20.0170.02110-3C25-30-103-10.024C25-30-103-20.021C25-30-103-30.0260.02410-4C25-30-104-10.021C25-30-104-20.011C25-30-104-30.0220.01810-5C25-30-105-10.021C25-30-105-20.018C25-30-105-30.0200.020

3 结 论

(1)随着张口位移速率的增加，混凝土的轴向拉伸强度和断裂韧度明显提高，以张口位移速率为10-5s-1时的轴向拉伸强度为准静态轴向拉伸强度，当张口位移速率达到10-4s-1，10-3s-1，10-2s-1时，对应的动态轴向拉伸强度分别提高9.8%，34%，60%。

(2)混凝土的临界位移大小与张口位移速率无关，是不随张口位移速率变化的混凝土材料参数值。

(3)混凝土的动态弹性模量随张口位移速率的增加而增加，且增长因子与张口位移速率比值的对数呈线性关系。

(4)通过对试验机及试验方法技术的改进，采用张口位移控制，理论上容易得到P-CMOD全曲线。后续研究工作可致力于研究带裂缝混凝土的P-CMOD全曲线。