超声导波针对均匀腐蚀的无基准评定方法

张耀烨，李冬生，周 智

(大连理工大学 土木工程学院，辽宁 大连 116024)

腐蚀对结构性能的影响具有时间跨度长、影响因素复杂、不确定性大等特点。检测信息的引入使人们可以更为客观地评价及预测结构的状态，继而做出合理的决策[1]。

超声导波作为一种精准、高效的无损检测技术已被诸多学者运用于土木工程构件的腐蚀监测中。文献[2]采用具有不同能量密度分布特征的导波进行钢筋混凝土构件剥离和坑蚀两种损伤模式的定性识别；文献[3]将分形理论运用于腐蚀监测；文献[4]则运用缺陷回波的幅值信息对钢绞线外围钢丝及中心钢丝的缺陷深度进行识别；文献[5]论证了缆索中钢丝间的接触会导致模态转换现象，并可将弯曲模态谱幅的变化作为评估损伤的指标。然而，考虑到长期的腐蚀监测过程中，换能器与构件界面的耦合性能将不可避免地发生改变，上述基于导波幅值信息测试结果尚缺乏可靠性，故研究人员尝试运用无基准的检测方法评估构件的性能。文献[6-7]中利用时间翻转法重构激励信号，通过一个用于刻画原始激励信号与重构信号畸变程度的指标来反映构件损伤的程度；文献[8]利用波达时间的改变量识别混凝土梁的剥离程度。近年来，基于模型的损伤识别方法被运用于导波监测中[9-11]，其突出的优点是可以准确地定量识别损伤。然而，腐蚀缺陷的形貌和位置具有随机性，用于模拟高频超声导波的数值模型往往难以兼顾计算效率和对缺陷的适应性，故并未见该方法在实际腐蚀工况下的运用。

导波的频散特性定量反映了群速度与频率的关系，随着频散方程地成功求解，一些典型波导的物理指标得以高效且准确地定量识别。吴斌等[12]对应双层结构波导的理论模型，研究了板(管道)表面附着水垢厚度对波速的影响；Amjad等[13]运用导波的频散关系对腐蚀后钢筋的不同直径量进行识别；Pierre[14]运用高阶SH模态频散曲线在频率轴上等间隔分布且具有截止频率的特点，定量识别管道局部腐蚀后的最小壁厚。但考虑到高阶扭转模态的可激发性和衰减特性，该方法难以运用于杆状波导中以定量识别较小的局部腐蚀缺陷。

现阶段的在线适时监测手段对工程中复杂的腐蚀行为(点蚀、疲劳应力腐蚀等)进行无损定量识别是极其困难的。为了满足对结构性能现状的评估及未来长期退化趋势预测的需要，人们多依赖由试验和统计资料获取的回归模型概括具体结构因腐蚀而导致的性能退化问题。通常情况下，对金属腐蚀状态评估的方法为：首先运用简便易行的剩余厚度测量获得均匀腐蚀量随时间变化的模型，继而建立复杂腐蚀行为或构件力学性能与均匀腐蚀的定量统计关系[15-18]。该方法虽然可以反映构件腐蚀作用下性能退化的共性规律，但很难基于有限的样本量提出一种广泛适用的模型。本文的观点在于：可通过均匀腐蚀监测数据与现有回归预测模型相结合的方法以定量评定更为复杂的腐蚀行为。运用这种策略不仅可通过引入监测数据减少预测模型针对个性结构腐蚀评定的主观不确定性，又可充分运用现有研究成果所揭示的共性规律较为准确、全面地评价各类腐蚀行为对结构性能退化的影响。这是符合现阶段健康监测水平和结构可靠性管理需要的。

本文将运用一阶纵向超声导波的频散特性，对加速腐蚀试验条件下钢丝的剩余直径量进行在线适时监测。同时，定量刻画时频分析中的不确定性对测量精度的影响，并发展一种高效评定均匀腐蚀的方法。

1 导波针对均匀腐蚀监测的相关理论

1.1 杆中的超声导波

杆中导波的类型分别为纵向模态、弯曲模态以及扭转模态。随着波导频厚积的增加，导波的多模态特性会突显，导致接收信号难以解析。L(0,1)模态无截止频率，衰减较小且具有良好的可激发性，通过设计对称的纵向振动激励接收方式可有效减少弯曲模态的影响[19]，故L(0,1)模态导波常被用于杆状构件的无损检测。

1.2 激励频率选择

杆件的均匀腐蚀表现为直径D的减少，故运用导波频散关系的无基线测试方法需要导波群速度Vg对直径改变具有较高的灵敏度，以便适时追踪腐蚀进程。在某一固定频率f下，式(1)显然成立

(1)

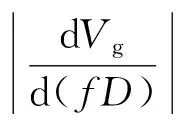
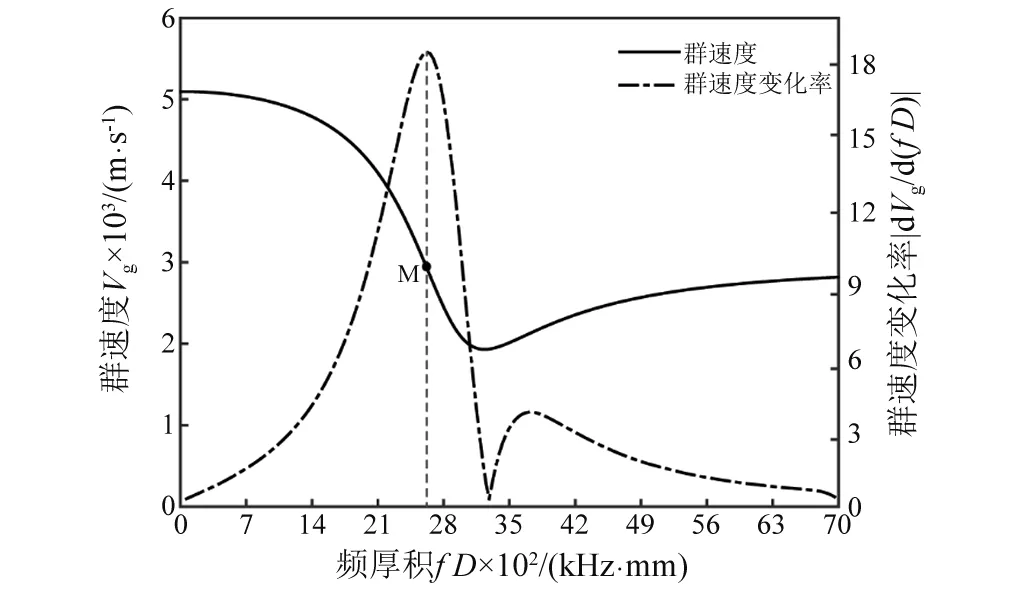
图1 L(0,1)模态群速度及其变化率曲线Fig.1 Group velocity of L(0,1) and its rate of change

1.3 时频分析的不确定性原理

对构件均匀腐蚀下剩余直径量的评定可归结为时频分析问题，其简化表达式为

(2)

式中：l为待测构件长度；f和t分别为接收信号的频率和波达时间；F为fD与Vg基于Pochhammer方程的对应法则；F-1为F的逆对应。

海森堡不确定性原理的本质是：较窄的时间波形产生较宽的频谱，而较宽的时间波形产生较窄的频谱，时间波形的宽度和其频谱宽度不可能同时任意小。定义时间持续期σt和带宽σω，则不确定性原理可由式(3)定义[20]

(3)

(4)

(5)

(6)

(7)

考虑到图1中M点附近接收信号频散较严重，故采用连续小波变换对接收信号进行时频分析。针对接收信号的时频不确定度分析可转化为与之具有最大相关性的小波基函数的时频不确定度分析。由于复Morlet小波在导波信号分析中运用广泛[21]，现就该小波时频不确定度表达式的具体形式做如下推导。

复Morlet小波母函数可定义为

(8)

式中：Fb为带宽参数；Fc为归一化(数字)中心频率且‖φ(t)‖2=1，故小波母函数基于归一化频率下的时域不确定度为

(9)

小波母函数经平移、缩放后的小波基函数可表示为

(10)

式中：s为尺度参数;u为平移参数，则小波基函数在归一化频率下的时域不确定度为

(11)

将归一化中心频率转化为模拟中心频率，则有尺度s1表示为

(12)

将式(9)、式(12)代入式(11)可得小波母函数在模拟频率下的时域不确定度为

(13)

(14)

将式(13)、式(14)代入式(11)可得时域不确定度表达式

(15)

(16)

2 导波对均匀腐蚀的试验研究

2.1 试验装置

监测对象为加速腐蚀试验条件下桥梁拉索用镀锌钢丝，直径为7 mm，总长约为103 cm，腐蚀段长度约为94 cm。电解质采用3.5%氯化钠溶液，钢丝设定为加速腐蚀系统的阳极，四片等间隔放置的不锈钢板设定为阴极，由外接直流电源提供恒定电流。采集系统套件包含机箱(PXIe-1073)，任意波形发生器(PXI-5441)及60MS/S、8通道数字信号采集板卡(PXIe-5105)。测量方式采用一端激励、一端接收。传感器采用相同的声发射探头(AE1045S)用于激励和接收纵向模态导波信号，其频率响应范围为0.1～1.5 MHz。激励信号采用射频功率放大器(AG1020)放大，接收信号采用前置放大器(PXPA6)放大。采用夹具将探头固定于待测钢丝两端，机油作为界面耦合剂以增加振动能量的传递效率。试验装置如图2所示。

图2 试验装置Fig.2 Experimental setup

2.2 频散曲线局部线性化

针对直径7 mm的镀锌钢丝，激励信号采用中心频率377 kHz的汉宁窗调制正弦信号，设定小波分析参数Fb=5，Fc=6，则归一化接收信号及其小波时频分析结果如图3、图4所示。假设接收信号相关性峰值点P的时间和频率为满足正态分布的随机变量，则对于复Morlet小波而言，两随机变量是独立的[22]，其联合概率密度如图5所示。由于在对直径进行评估的随机模拟的过程中，将涉及到对复杂的Pochhammer方程的多次求解，按式(17)在M点((fD)M,VgM)处将F线性展开为FL，即

(17)

将式(17)代入式(2)可将其转化为具体的显式二元测量函数以提高随机模拟的计算效率。如图6所示，在频厚积为2 320～2 880 kHz·mm内，FL在求解Vg时具有极高的精度，其相对误差小于1%。

图3 接收信号Fig.3 Received signal

图4 复Morlet小波时频分析结果Fig.4 Result of time and frequency analysis based on complex Morlet wavelet

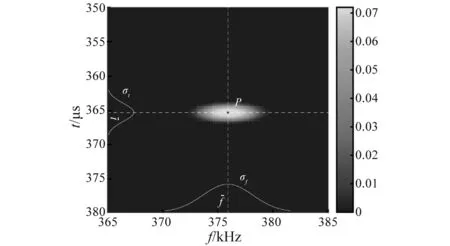
图5 时间-频率联合概率密度Fig.5 Joint probability density of time and frequency

图6 频散曲线局部线性化Fig.6 Local linearization of dispersion curve

2.3 自适应MCM及GUM法

在测量不确定性的评定中，蒙特卡洛法(Monte Carlo Method，MCM)是一种通过重复采样实现分布传播的数值方法。通过对测量模型Y=g(X1,X2,,Xn)中输入量Xi的概率密度函数离散采样，由测量模型传播输入量的分布, 计算获得输出量Y的概率密度函数的离散采样值, 进而由输出量Y的离散分布数值直接获取输出量的最佳估计值y、标准不确定度uy和规定包含概率p下Y的最短包含区间端点ylow和yhigh。由于传统的MCM所需的试验次数跟输出量的分布形式、包含概率及规定的数值容差等因素有关，为了消除主观设定样本量对试验结果的影响，本文采用自适应MCM实现分布传播的数值求解。自适应MCM[23]是在执行传统MCM的基本过程中，程序自动增加试验次数，直至输出量结果最终达到统计意义上的稳定，其收敛准则为输出量的两倍标准偏差均小于uy的数值容差δ，即

(2sy<δ)∩(2su(y)<δ)∩(2sylow<δ)∩ (2syhigh<δ)

(18)

GUM法是国际标准[24]中所规定的测量不确定度评定方法。GUM法将测量模型的输出量近似为正态分布或缩放位移t分布，当Xi相互独立时，y的合成不确定度可由式(19)获得

(19)

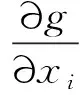
2.2 学龄前儿童缺铁性贫血影响因素的单因素分析 单因素分析结果显示，年龄、出生体质量、喂养方式、消化功能、辅食添加时间、妊娠期贫血情况、父母亲的文化程度、家庭饮食习惯、铁制剂服用情况、家庭收入为学龄前儿童缺铁性贫血的影响因素(P<0.05)。见表1。

在规定包含概率p下，包含区间端点可表示为

Y=y±Up=y±kpuc(y)

(20)

即Y的值以概率p落在[y-Up,y+Up]区间内，Up和kp分别为包含概率p下的扩展不确定度和包含因子，取p=95%，kp=1.96。

2.4 自适应MCM及GUM法对比验证

GUM法简单易行且对许多问题具有适用性，然而当测量模型的非线性程度过高或输出量的分布明显不对称时，GUM法对输出量的评价结果可能会变得不可靠。自适应MCM的适用范围更广泛，可以得到指定输出精度的结果，可作为一种手段验证GUM法的适用性。依据式(17)，运用自适应MCM及GUM法两种方法，对结果包含区间各自端点的绝对偏差进行比较

dlow=|y-Up-ylow|≤δdhigh=|y+Up-yhigh|≤δ

(21)

若结果满足式(21)，则可运用GUM法代替自适应MCM高效地进行直径评估。

自适应MCM可自动调整采样次数而使得直径评价结果达到设定精度范围内的稳定。传统MCM则采用了规范建议的试算次数。较自适应MCM，传统MCM法由于采样次数过少，其输出量在95%包含概率下的最短包含区间端点显然不满足设定精度要求。GUM法可通过自适应MCM验证，即在设定的精度范围内可运用GUM法评定剩余直径量。

图7 直径的概率密度Fig.7 Probability density of diameter

表1 自适应MCM验证GUM法Tab.1 GUM verified by self-adaptive MCM

2.5 试验结果分析

外接电流恒定为0.35A，每隔12 h对钢丝剩余直径量进行监测，直径改变步长由法拉第定律控制，约为0.05 mm。图8例举了在腐蚀监测初期(0～48 h)，维持激励频率为377 kHz不变的情况下接收信号的时频分析结果。接收信号的相关性峰值点频率会随着腐蚀进程而略有偏差，但波达时间仍明显地呈现出单调减小趋势，证明导波群速度对钢丝直径的变化是极为敏感的。

图8 0～48 h波达时间变化趋势Fig.8 Time of flight within initial 48 hours

图9为超声导波对钢丝剩余直径的评定结果。首先，导波评估结果具有较高的精度，其与理论值的绝对误差小于0.157 mm；其次，评估的剩余直径量随着腐蚀时间的增加单调递减，进一步说明了导波评价手段针对直径变化具有极高的分辨率；另外，绝对误差在腐蚀后段具有逐渐增大的趋势，分析原因为：①腐蚀速率与电极距有关，钢丝由于表面腐蚀速率不同，在发生均匀腐蚀的同时局部腐蚀效应也逐渐突显，表现为钢丝不同区段的直径差异增大；②表面逐渐积累的腐蚀产物会影响导波在钢丝中的传播特性，导致波速与理论值产生偏差；③后期表面积累的腐蚀产物会较大程度地影响导波在钢丝中的衰减特性，接收信号幅值衰减严重，信噪比明显下降。最后，基于时频分析对直径评估的“测不准”特性，GUM法的分析结果提供了可靠的区间估计。当腐蚀时长在250 h范围内，评估结果的随机性与分析结果吻合良好，但随着腐蚀时长的进一步增加，由于外界影响因素的介入将导致评估结果的误差增大，表现为置信区间外的异常值数量增多。

图9 导波评估结果Fig.9 Evaluation of guided waves

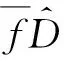
3 结 论

(1) 本文发展了一种基于超声导波针对剩余直径量的无基准评定方法。该方法在群速度随频厚积改变最为敏感的区段内选择激励频率，利用导波的频散关系实现了对剩余直径的高精度定量评定。

(2) 推导了将复Morlet小波运用于时频分析中时，接收信号波达时间与频率不确定性的定量表达式。比较验证了自适应MCM与GUM法输出结果的等效性，证明GUM法可用于钢丝均匀腐蚀程度的快速评定。

(3) 点蚀、疲劳应力腐蚀等与均匀腐蚀的定量统计关系常被作为评价复杂腐蚀行为对构件性能影响的手段。基于导波所获取的高精度均匀腐蚀监测数据可进一步结合既有的研究成果以用于各类腐蚀评定，从而有效降低构件性能评价及预测过程中的主观不确定性。