基于时序模型和自联想神经网络的齿轮故障程度评估

张 龙, 成俊良，杨世锡, 李兴林

(1. 浙江大学 机械工程学院，杭州 330027; 2.华东交通大学 机电与车辆工程学院，南昌 330013；3.杭州轴承试验研究中心 博士后工作站，杭州 310022)

齿轮及齿轮传动装置作为传递动力的常用零部件，其失效是诱发机械系统故障的主要原因之一,因此齿轮故障诊断得到了广泛研究。齿轮故障诊断偏重于故障性质及发生部位的识别，而近年来逐渐成为研究热点的预诊断则关注设备有效剩余寿命预测问题[1-4]。

基于信号处理的设备状态特征提取是故障诊断与预测的前提，常见方法主要有时域处理(峰值、均方值、峭度、时域同步平均等)、频域处理(傅里叶变换、倒频谱、短时傅里叶变换等)、时频域处理(Wigner-Ville分布、小波变换、经验模态分解)、时间序列分析法(自回归滑动平均模型、自回归时序模型)等[5-11]。其中，时间序列分析法，尤其是基于自回归时序(Autoregressive, AR)模型的时间序列分析，其模型参数包含了系统的重要状态特征且对系统的状态变化非常敏感，在故障特征提取中得到了广泛的应用。如于德介等采用经验模态分解(Empirical Mode Decomposition, EMD)EMD方法和AR模型相结合来提取滚动轴承振动信号的特征向量，然后建立Mahalanobis距离判别函数来识别滚动轴承工作状态并判断故障类型。Cheng等[12]则在EMD与AR模型结合的基础上引入支持向量机模型，结果显示该方法能够在更少样本情况下准确判断齿轮状态。

由于智能算法在故障模式识别中取得的良好效果，一些基于概率相似度量的故障程度评估模型相继被提出，如高斯混合模型(Gaussian Mixed Models, GMM)、隐马尔科夫模型(Hidden Markov Model, HMM)等。基于概率相似度量的故障程度评估模型的核心是建立正常数据的密度模型来进行异常检测，如Heyns等[13]提出一种角域同步平均和高斯混合模型相结合的齿轮状态监测方法，将齿轮每圈的振动信号按齿数进行分割，利用GMM计算每段信号与无故障状态的相似度系数，最后将这些系数进行同步平均以判断故障位置和故障程度。曹端超等[14]则利用改进EMD进行故障特征提取，用特征矢量训练HMM，以最大对数似然函数输出来表征齿轮的故障程度。

基于概率相似度量的故障程度评估模型期望通过合适的信号处理方法进行深层次信息挖掘，以提高故障程度评估的敏感性、一致性和鲁棒性。然而实际应用中尚存在一些问题：①需要足够大的训练集用以训练模型；②可能会出现过早饱和的情况，当测试样本与无故障基准模型之间相似度为零时，设备可能并未完全进入失效状态，即存在模型极限值的出现早于真实物理失效的情况。

基于重构的故障程度评估模型则通过重构数据来提取数据间的相互关系，以无故障样本建立基准模型，以数据重构的差异来衡量故障程度。如王建利[15]利用希尔伯特黄变换提取信号各模态分量包络谱作为故障特征，结合自组织神经网络实现滚动轴承的故障程度评估。重构模型利用重构错误(比如欧式距离)来判断输入数据的故障程度，避免概率相似度量模型的过早饱和问题。

自联想神经网络(Auto-Associative Neural Network, AANN)属于重构模型，由Kramer[16]于二十世纪九十年代首次提出。AANN是一种特殊的前向结构网络，训练过程中网络的输入与输出一致，通过信息的压缩与恢复来拟合模型，使之契合测量数据内部的相关性。对于训练后的网络，通过比较重构样本和输入样本的偏离程度，可评估机械结构的健康状态。本文利用AR模型提取信号状态特征，以其系数作为AANN的输入，利用正常工况下的数据样本训练AANN，对输入样本进行重构，结合提出的均方根差值故障程度指标实现齿轮的故障程度评估。

1 时间序列分析

AR模型是一种基于有理传递函数的参数化建模方法，模型的系数包含了信号的状态特征，且对其变化十分敏感。本文将AR模型的系数作为自联想神经网络分析的输入参数，建立模型前对输入信号进行标准化处理

(1)

(2)

式中:αj为第j项的系数;e(t)为AR模型的残差，AR模型的参数估计就是选择合适的参数使模型的残差e(t)为白噪声。

2 自联想神经网络

自联想神经网络是一种前馈型神经网络，其思想了来自于主成分分析和非线性主成分分析，用于在信息损失尽可能小的前提下将高维空间的数据映射到低维特征空间。

设Y为n×m维矩阵，n为测量次数，m为变量的维数，从测量空间到特征空间的非线性映射可以表示为

T=G(Y)

(3)

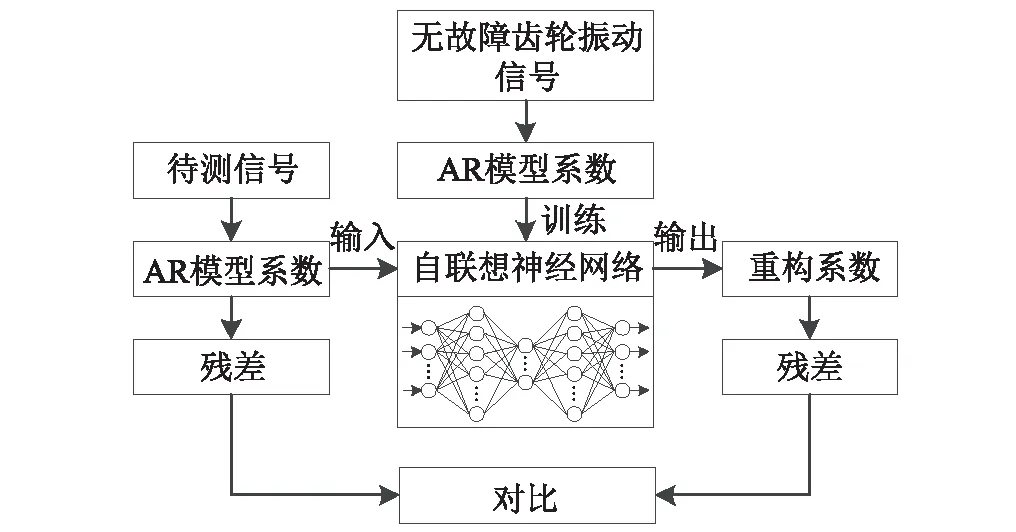
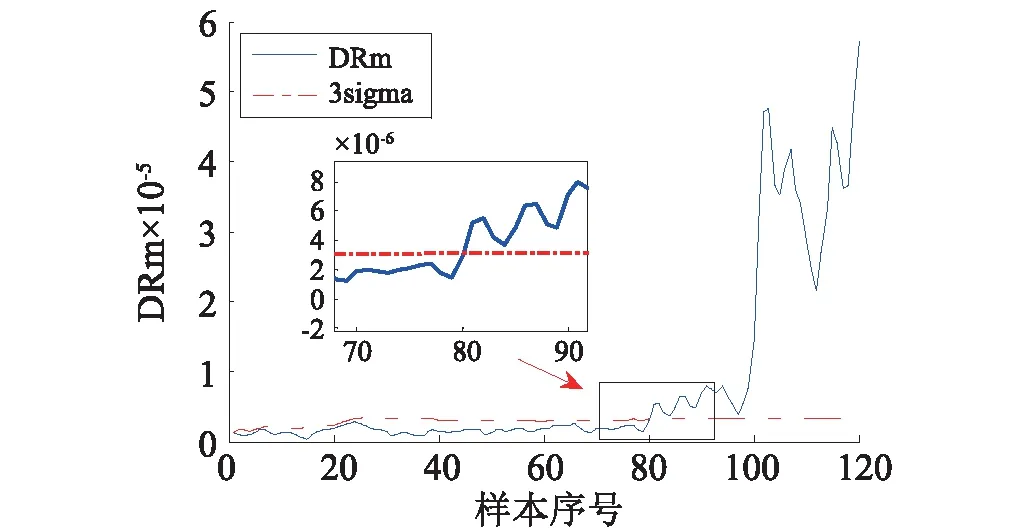
式中:T=[t1t2tf]为主成分矩阵(n×f)，f为主成分个数(f

从特征空间到测量空间的非线性逆映射可以表示为

Y′=H(T)

(4)

式中:Y′为n×m维矩阵，通过逆映射的非线性函数H将数据恢复为原始维数。

相比于一般的BP神经网络，自联想神经网络有两个特点：①训练时网络的输入和输出相同，训练的目标是寻找输入参数间的相互关系；②网络层数更多，包含三个隐层：映射层、瓶颈层和解映射层。加上输入层和输出层，一共五层结构，如图1所示。

图1 自联想神经网络结构Fig.1 Auto-associative neural network

输入层、映射层和瓶颈层将原始数据压缩到低维特征空间(实现G)，完成输入数据的压缩；瓶颈层、解映射层和输出层三层结构则将特征空间的数据解映射到输出层(实现H)，完成输入数据的重构。瓶颈层是自联想神经网络的关键，其节点个数明显少于其他层，完成内部编码和信息压缩。同时，为了防止输入和输出之间形成简单的一一映射，除了输出层激励函数采用线性之外，其他层均采用非线性激励函数。

自联想神经网络所学习的是数据间的相关性，训练中信息量的丢失可以通过输入和输出之间的差值来衡量，并以式(5)作为网络训练的目标函数

(5)

3 故障程度评估模型和报警阈值

基于AANN的齿轮故障程度评估模型，如图2所示，包括两个步骤：神经网络的训练和预测。训练阶段利用无故障样本的AR系数作为输入输出训练AANN，通过对数据不断的压缩重构，拟合AANN中各节点的权值，使AANN契合无故障数据的内部相关性，得到基准评估模型。预测阶段将齿轮振动信号的AR系数作为基准评估模型的输入，由于AANN是由无故障信号的AR系数训练得到，当输入信号无故障或故障程度较低时，AANN重构所得AR系数与输入AR系数内部相似度较高；但随着输入信号故障程度的增加，AANN重构所得AR系数与输入AR系数的差别将逐渐增大。

AANN的输出是对输入重构后的AR模型系数，虽然其包含了信号的状态特征，但并不能直接显示齿轮的故障程度。因此，将AANN重构后得到的AR模型系数(AANN的输出)与原始AR模型系数(AANN的输入)分别代入输入信号的AR模型中，进行时序建模并得到残差序列，对比所得到的两列残差序列，即可评估齿轮的故障程度。

图2 齿轮故障程度评估流程图Fig.2 Flow chart of gear fault severity assessment

3.1 故障程度指标

齿轮故障程度由两列残差序列的差异来表现，但残差的直接对比对故障程度的揭示尚不直观，信号的均方根值(Root Meam Square, RMS)能直接反映信号的能量，其表达式为

(6)

式中:x为信号值；k为长度；xrms为信号的均方根值。

计算两个残差序列的均方根值，其差值如式(7)所示

Dvalue=xesr-xess

(7)

式中:xess为信号原始AR模型系数下AR模型残差序列的均方根值；xesr为AANN重构得到AR模型系数下AR模型残差序列的均方根值。

考虑到指标应与原始AR模型系数下残差的均方根值关联性更强，本文提出一种无纲量故障程度指标：均方根差值DRm(D-value of root mean square, DRm)，如式(8)所示

DRm=(xesr-xess)×xess

(8)

3.2 自适应报警阈值

本文提出的故障程度指标DRm是一个连续变化的指标参数，表示齿轮偏离正常状态的程度。设定该参数的报警阈值有利于工作人员掌握设备运行状态。

根据概率统计中的3σ准则，对于标准差为σ均值为μ的正态或近似正态分布样本数据，样本数值分布在(μ-3σ,μ+3σ)的概率为0.997 3。因此可以假设处于相近故障程度下的DRm值也符合一定的正态分布，一旦连续多个DRm值超过前面DRm值确定的3σ范围，则认为故障程度已发生较大改变[17]。该阈值根据DRm值得到，具有自适应性，由于DRm值总体呈上升趋势，故只计算阈值上限，即μ+3σ，如式(9)所示

(9)

式中: {x(i),i=1, 2,,n}为t=[1,n]时刻的DRm值;T(t)为t时刻的报警阈值。当第一次连续多个时刻的DRm值超过te时刻的阈值T(te)时，定义te为故障严重程度或性能退化状态发生变化的时刻。

4 试验数据分析

4.1 不同故障程度试验数据

试验数据来自一个四速摩托车变速箱，驱动电机转速为1 420 r/min，信号采样频率16 384 Hz。

Rafiee等[18]在该变速箱上模拟了三种齿轮故障状态：轻度磨损、中度磨损和断齿。三种状态下的时域波形如图3所示。三种故障模式下的齿轮箱振动信号中，轻度磨损和中度磨损两种故障模式的故障程度比较接近，断齿故障模式下的加速度信号故障较明显，出现明显冲击。

图3 三种状态下齿轮箱振动信号Fig.3 Vibrations of gearbox with three different fault levels

图4是轻度磨损、中度磨损和断齿三种故障模式信号的频谱图，从图中也可以看出断齿信号的频谱较易识别，但轻度磨损和中度磨损信号由于频谱峰值内容比较相似而难以区分。

利用本文提出的性能退化评估方法分析三种故障程度信号，根据信号的转频，将轻度磨损信号中每704个采样点作为一个样本，中度磨损信号中每680个采样点作为一个样本，断齿信号中每708个采样点作为一个样本。取50个轻度磨损样本作为训练集对自联想神经网络进行训练，再取50个轻度磨损样本、50个中度磨损样本和50个断齿样本组合成150个样本的测试样本作为测试集检验方法的有效性。评估结果如图5所示，轻度磨损样本的DRm值较低，中度磨损样本对应的的DRm值达到了100左右，断齿样本的DRm值则达到450以上，说明本文所提出故障程度评估方法可清晰反映齿轮故障程度的变化。

图4 图3中三种不同故障程度的频谱图Fig.4 Spectral of the signals illustrated inFig. 3

图5 图3中三种不同故障程度的DRm值Fig.5 DRm values of the signals inFig. 3

4.2 齿轮全寿命试验数据

为进一步验证本文方法的有效性，采用法国Jean Monnet University的LASPI信号处理与工业工程实验室和法国Cetim Senlis提供的齿轮全寿命试验数据进行分析[19]。试验对象为一个一级减速齿轮箱，输入和输出轴上齿数分别为20和21，详细参数见表1。振动加速度信号的采样频率20 000 Hz，齿轮的啮合频率为330 Hz，每天采样一次，每次3 s。每天停机一次观测齿轮的损伤情况，在第12天发现第16齿全齿面剥落后停机。每日肉眼观测齿轮状态结果，如表2所示。

齿轮测试过程中采集到振动信号的时域波形如图6所示，从图6中可以看出，第1天～第10天时域波形的振动幅值变化不大，但在第11天，振动幅值突然大幅增加，齿轮进入了失效状态。

表1 齿轮箱参数Tab.1 Gearbox characteristics

表2 齿轮箱每日停机观测结果Tab.2 Gearbox daily shutdown assessment report

图6 齿轮全寿命数据时域波形Fig.6 Time domain waveform of the whole run-to-failure test

图7 齿轮故障照片Fig.7 Photos of gear spall faults during the test

图7(a)为第10天第2齿照片，图7(b)为第10天第16齿照片，图7(c)为第11天第16齿照片。从图7中可以看到，第10天第16齿的故障程度与第2齿的故障程度相当，而第11天第16齿的剥落面积迅速增大。结合图6齿轮时域波形可知，齿轮的失效是由于第16齿的故障加深产生，第2齿的故障一直保持在较低水平。

提取基准阶段AR模型系数前应先对信号进行预处理：首先，对信号进行时域同步平均，减小信号中的随机误差，根据齿轮转频可求得平均点数应为1 200；其次，故障程度指标DRm由信号的有效值得到，对信号的能量较敏感，但振动信号中齿轮啮合频率所含能量较高，故还需进行数字滤波，将齿轮啮合频率及其前六阶谐波的左右三条谱线全部置零，消除齿轮啮合干扰；另外，为了满足神经网络训练样本数量的要求，将每天采集的60 000点数据分为10个样本，每个样本6 000个数据点，全寿命周期共120个样本。

利用所提出的诊断方法对120个样本进行分析，首先以前35个样本作为训练集训练自联想神经网络；然后利用所得评估模型对齿轮的全寿命数据进行分析，所得故障程度评估结果，如图8所示，实线表示式(8)得到的故障程度指标DRm值，虚线为式(9)得到的自适应报警阈值。考虑故障程度的渐变性和噪声的干扰，对得到的DRm值做了平滑处理，即图中的每个点都是由它本身和前后两个点线性拟合得到。

图8 前35个样本作为训练集时评估模型所得DRm值Fig.8 DRm values obtained from the assessment model with the first 35 samples as training set

由图8可知，前四天DRm值较低，设备处于正常运行状态。第5天DRm值增加并超过3σ报警阈值，出现早期故障，达到0.3×10-5左右。随后3σ报警阈值在当前故障程度下自适应提高，达到0.5×10-5。在第9天DRm值迅速增加，至0.7×10-5附近，再次超过了3σ报警阈值，故障程度加深。第11天DRm值增加至3.5×10-5左右，从时域波形也可看出，振动幅值跳跃性增大，齿轮失效。

表2中齿轮箱的停机观测结果显示，齿轮箱第16齿在第8天已经出现早期剥落，而DRm值在第9天才明显增加，其原因为第8天出现早期剥落后故障程度并不高，随着剥落的发展，故障程度不断加深，第9天故障程度的增大使得DRm值在第9天显著增加。另一点，表2中齿轮箱第2齿第6天才出现剥落，而DRm值在第5天已经超过3σ报警阈值，判断出现故障。分析结果与观测结果不一致。其原因有两种：一是本文所提出的故障程度评估方法出现误报，方法还需改进；二是第2齿第5天已经出现剥落裂纹，但由于裂纹较小且处于表层以下并未完全剥落，观测人员并未观测到，从而认为第5天并未发生故障。

为了确认问题的原因，对数据进行进一步分析。由DRm值水平可知，若第5天第2齿已经出现剥落裂纹，那么第6、第7、第8三天应认为处于同一故障水平。如果以前五天的样本作为训练集训练自联想神经网络，第6、第7、第8三天也应被诊断为无故障状态，DRm值将与前五天保持同一水平。图9为用前五天的样本作为训练集，自联想神经网络得到的DRm值。从图9中可以看到，DRm值一直到第8天均保持在较低水平，至第9天才超过报警阈值，因此可以确定第2齿故障在第5天就已经出现。

图9 前50个样本作为训练集评估模型所得到DRm值Fig.9 DRm values obtained from the assessment model with the first 50 samples as training set

文献[20]也对该齿轮全寿命数据进行了分析，利用耦合隐马尔科夫模型对该组齿轮数据进行全寿命故障程度评估。评估结果如图10所示，齿轮的性能退化过程分为四个阶段：第一阶段1～5天，指标几乎没有变化；第二阶段6～8天，指标出现波动，但幅度较小，诊断为轻微故障；第三阶段9～10天，指标出现明显降低，超过一级报警限；第四阶段11～12天，指标迅速降低，呈断崖式下跌，齿轮严重失效。

图10 耦合隐马尔科夫模型评估结果 (摘自文献[20])Fig.10 Results from coupled Hidden Markov Model (from[20])

与之相比，本文所提出方法也成功评估第9天和第11天故障程度的加深。更进一步，本文方法成功诊断出第5天第2齿出现的早期故障，对于前期微弱故障的诊断更加敏感；另一方面，两种方法都没有诊断出16齿在第8天出现的早期剥落，其原因应是对该故障的响应被第2齿剥落的响应淹没，也从一个方向说明方法对故障类别的区分还有待加强。但在故障程度评估方面，本文方法能够对故障程度准确表达。

5 结 论

(1)利用AR模型提取齿轮箱正常工况下振动信号的状态特征，训练自联想神经网络，训练后的神经网络可根据输入信号准确评估齿轮的故障程度。

(2)DRm指标对于早期故障十分敏感，对故障的诊断基于信号的宏观能量，因而其对于故障分布和类别的区分还有待提高。但作为齿轮性能退化的指标，DRm可以完成对故障程度的评估。