高精度偏置内抛物面的数控加工方法*

严瑞强，楚 功，门延会 ，肖善华，甘 露

(1.宜宾职业技术学院，四川 宜宾 644000；2.五粮液集团有限公司，四川 宜宾 644000；3.中核建中核燃料元件有限公司，四川 宜宾 644000)

0 引言

某企业的反射装置零件有偏置内抛物面需要加工，过去采用的是直线逼近方法在数控车床上加工，这种加工方法虽然编程简单，但加工精度不高。对于有外抛物线轮廓零件的加工，已有大量文献反映了相应的研究成果[1-5]。对零件内抛物面的加工未见相关研究成果。为满足生产需要，现采用了等间距直线逼近法对内抛物面进行粗加工，圆弧逼近法对内抛物面进行精加工，解决了零件偏置内抛物面加工精度不高的问题。

1 内抛物面零件粗加工

薄壁内抛物面零件开口向右，如图1所示，是某企业零件反射装置的重要配件。尺寸精度、形状精度和位置精度要求高，加工质量保证不了，生产出来配件就会有振纹、反射不成型等严重质量问题。

1.1 粗加工数学模型

图1 内抛物面零件

为了保证精加工工序背吃刀量一致，我们可以通过制图软件，画图查点，用G71指令编制留有均匀余量简单实用的粗加工程序，缺点是必须熟悉制图软件。同理，利用抛物线方程，安排合理的加工工艺，用宏指令设计循环，能方便快捷高效地完成抛物线内轮廓部分的粗加工。

1.2 粗加工宏程序

O9001；

T0101M3S550；

G99G0X19Z5；

#110=20 ；//X坐标赋初值

#111=40；//X坐标终点值

#112=0.5；//X向精加工余量

#113=0.2；//Z向精加工余量

#114=14；//X向平移量

#115=38；//Z向平移量

WHILE[ #110 LE#111]DO1 ；//循环条件判断

#116 =[#110-#114]*[#110-#114]/20-#115；

//计算Z坐标值

#117=#110-#112；//X向留精加工余量

#118=#116+0.2：//Z向留精加工余量

G1X[2*#117]Z[#118]F0.3；//直线插补加工抛物线

U-1；//X负方向退刀

G0Z5；//Z向退刀

#110= #110 + 1；//X向层切深递

END1；//循环结束

M30；

2 圆弧逼近精加工

2.1 数学模型的建立

计算非圆曲线上任一点的曲率半径值，是解决圆弧逼近非圆曲线的关键点和难点。

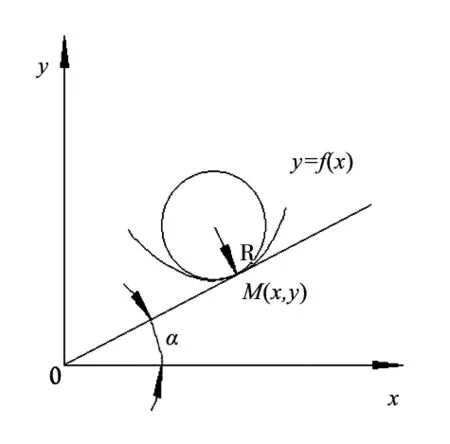
图2 曲率半径数学模型

见图2，设曲线y=f(x)，并且f(x)具有二阶导数，s是曲线上固定点M的弧长，α是切向角，ρ是曲率。

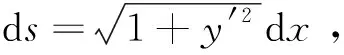
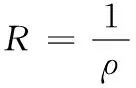
(1)

2.2 精加工宏程序

圆弧逼近法内抛物面精加工宏程序编制如下：

O9002；

T0202M3S1000；

G99G0X80Z2 ；//快进到切削起点

G1Z0F0.1；//直线插补

#110=40；//X坐标赋初值

WHILE[ #110 GE20]DO1 ；//循环条件判断

#116 =[#110-14]*[#110-14]/20-38；//计算Z坐标值

#117=1+[[#110-0.5] /10-1.4]* [[#110-0.5] /10-1.4]；//计算中间点的值

#118=10*SQRT[#117] ；//计算曲率半径R的值

G3X[2*#110]Z[#116]R[#118] ；//圆弧插补逼近曲线加工

#110=#110+1 ；//X坐标深递

END1 ；//循环结束

G1U-1 ；

G0Z5；

M30；

3 加工试验

为了验证该加工方法的可靠性，在相同条件，拟采用等间距直线逼近法、等步长直线逼近法、圆弧逼近轮廓法进行试验验证。通过实际加工检测，上述3种逼近方法加工结果对比如表1所示。

表1 3种逼近方法的加工结果对比表

从表1中可以看出，圆弧逼近的精度和表面质量远高于直线逼近的精度和表面质量。

将设计出的两个程序在FANUC 0i-TC机床上运行后，轨迹显示见图3，加工出的实物见图4，经检验零件尺寸精度、形位精度符合设计要求。

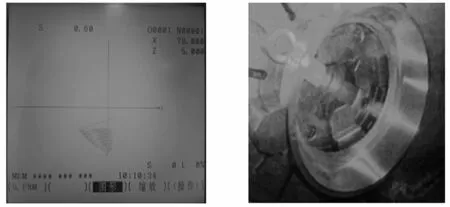
图3抛物线轨迹 图4内抛物面实物

4 结论

基于圆弧插补原理，编制宏程序，在FANUC 0i-TC数控机床上，进行加工验证。结果表明，采用等间距直线逼近法对零件内抛物面进行粗加工，圆弧逼近法对零件内抛物面进行精加工，使零件尺寸精度提高了两个公差等级，表面粗糙度达到0.4μm，有效的保证了高精度零件的加工质量，这对同类复杂形面零件的加工具有较高的参考价值。