基于历史告警数据的计量异常事件关联度分析
蔡 毅,廖绍成,杨 培,李 璟,郭 倩,赵立美
(1.国网浙江新昌县供电有限公司,浙江 绍兴 312500;2.中国计量大学 机电工程学院,杭州 310018;3.浙江华云信息科技有限公司,杭州 310008)
0 引言
电力工业是关系国计民生的基础性产业,现代电能计量是电力用户与供电单位之间的结算依据,因此,对电能计量异常分析与处理就愈发重要[1-2]。计量异常报警是用电信息采集系统的一个重要功能模块,异常报警功能对用电现场的异常情况设置报警标志,报警标志可以由系统实时查询或由终端主动上报[3]。正确分析判断用电信息采集平台上所反映出来的异常事件和异常数据,就能够实时监测和监控用电现场的运行状况,有针对性地判断用户的用电情况是否有异常,降低由电能计量故障所带来的损失[4]。针对单个计量异常告警事件,通过异常原因分类、处理流程、异常现象及处理步骤的研究总结,已经有较规范统一的处理流程和方法[5-10]。然而,日常运行中的计量异常种类繁多、情况复杂,用电信息采集系统发出的事件告警信息混杂在一起,仅对单个计量异常报警事件进行分析,常常造成误报、漏报等问题,导致工作量大,难以进行有效地分析处理及应用。因此,对计量异常事件之间的关系进行研究,建立计量异常事件关联度的计算模型,将存在关联的异常事件组合视为并发异常事件处理,是提高计量异常事件分析效率和准确性的关键所在。
在电力系统中,常用的关联分析方法主要有皮尔逊相关分析法和灰色关联度分析法。皮尔逊相关分析法是一种计算线性相关性的方法,其基本原理是通过变量之间的协方差和标准差的商来计算皮尔逊相关系数;灰色关联分析方法的基本思想是根据序列曲线几何形状间的相似程度来判断其联系是否紧密,曲线越接近,相应序列之间的关联度就越大,反之就越小。文献[11]在大数据应用原则和大数据思维的指导下,融合电力设备故障统计数据和电能质量监测数据,采用皮尔逊相关分析法对二者的关联度进行了分析;文献[12]针对电网安全运行评价的需要,采用灰色面积关联分析法确定评价模型的分辨系数,提出了一种基于多层次灰色面积关联分析法的电网安全综合评价模型;文献[13]采用灰色关联规则分析方法对变压器故障信息数据进行挖掘,对变压器故障与特征量之间的可信度进行分析,揭示了变压器故障与特征量的相关程度。这些关联度分析方法均对分析数据有要求,需要具体采样数据,并不适用基于异常事件发生时间的关联度分析。
本文通过对用电信息采集系统中的历史告警数据进行分析,提出一种基于异常事件发生日期间隔天数的两两计量异常事件关联度计算方法,对现有数据进行分析,明确关联分析方法,选取异常发生日期间隔天数对关联度进行计算;构造关联系数函数,确定关联分析流程,设置阈值,实现对并发异常事件的甄别;对关联分析结果进行分析。实例计算结果表明,该方法能够准确计算出两两计量异常事件之间的关联度,对存在关联的计量异常事件组合进行有效筛选。
1 数据分析
现有数据为某市2015—2016年专用变压器(以下简称“专变”)用户和低压用户同月同一用户出现多种异常的历史告警数据。每条告警记录都包含了用户编号、异常类型名称、异常发生时间、异常恢复时间和异常归档时间等信息,其具体记录方式如表1所示。
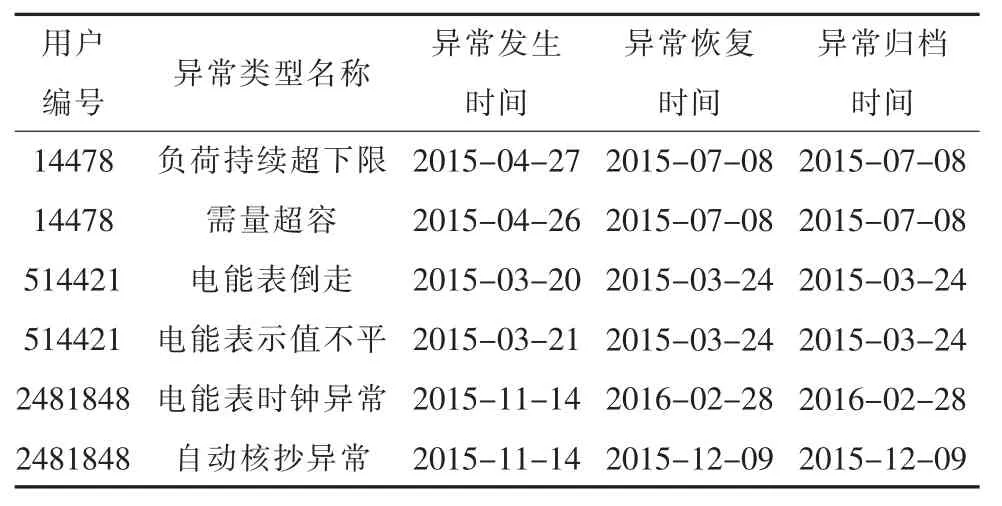
表1 异常告警数据记录
由表1可知,异常恢复时间和异常归档时间相同,异常恢复时间和异常发生时间有一定间隔,但间隔时间长短不一,原因是异常恢复时间受人为因素影响。对于要纳入考核的计量异常事件,一般会在一周内进行人工恢复;而对于不进行考核的异常事件,恢复时间视现场运行情况和工人工作安排而定。对于恢复时间与发生时间相差过大的异常,其恢复时间多为后期归档时填写的归档时间,并非实际恢复时间。因此,在历史告警数据中实际可用来进行关联度分析的数据只有异常发生时间,而异常恢复时间受人为因素影响较大,并不准确。本文在对现有数据进行充分剖析的基础上,以异常事件发生时间为参考,构建了基于异常发生时间间隔天数的关联度计算模型。
2 关联分析方法
2.1 关联分析原理
令A1为异常事件1,A2为异常事件2,通过对大量历史数据进行分析发现,A1和A2总是同时或者前后紧接着发生,可以初步认为这2种异常事件可能有关联;再根据异常发生日期间隔天数构造关联系数函数,分别求出每一次的关联系数r,如果关联系数波动较小,集中分布在某一区间内,则认为A1与A2有关联,对该区间的关联系数取均值即可求出A1和A2的关联度;反之,如果关联系数分散分布,则认为A1和A2的关联度为0。
2.2 关联分析流程
2.2.1 关联系数函数构造
对于同一用户,2个异常事件之间的关联系数r与异常发生日期间隔天数d成反比关系,即随着间隔天数d的增大,关联系数r逐渐减小。由理论上分析知,如果A1与A2为一组并发异常事件组合,则A1与A2应该由同一异常原因引发。通过对填写了异常原因的档案数据进行分析发现,当2个异常事件发生日期间隔超过15天时,由同一原因引起的概率小于5%。统计学上通常将发生概率小于5%(即1/20)的事件称为小概率事件[14]。因此,排除小概率事件,将异常发生日期间隔天数d的阈值定为15:当d>15时,认为无关联,不进行关联系数计算;当d≤15时,一个异常恢复后另一个异常才发生,也认为无关联,不进行关联系数计算;当d≤15且一个异常恢复前另一个异常发生,关联系数计算式为:
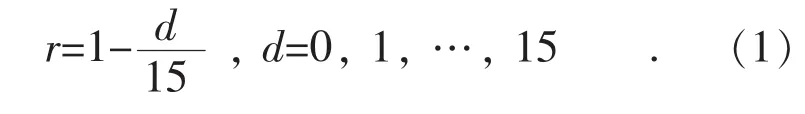
2.2.2 确定可能存在关联的两两异常事件组合
首先,对历史告警数据进行分析处理,得到2年来所有出现过的计量异常事件种类共K类,分别求出每种异常事件在2年内出现的次数nk;其次,对所有的异常事件进行两两组合,分别求出第i种异常与第j种异常组合时,间隔天数d≤15,一个异常恢复前另一个异常发生且为同一用户的次数nij;最后,设置阈值η,当nij大于阈值η时,可初步判断2种异常事件可能有关联。该阈值应排除小概率事件,即当nij大于单异常事件在2年内出现的总数的1/20时,认为2种异常事件可能有关联。阈值η的计算公式为:
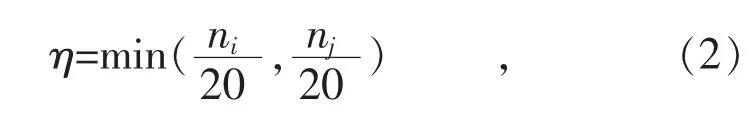
式中:ni表示第i种异常在2年内出现的总次数;nj表示第j种异常在2年内出现的总次数。
2.2.3 对可能存在关联的异常事件组合进行关联分析
初步确定两计量异常事件可能具有关联后,根据式(1)分别计算出这nij次每次的关联系数rs(s=1, 2, 3, …, nij), 令l=0,1, …,15)为关联系数rs在区间[0,1]上所有可能取值,pl=l=0,1,…,15)为关联系数在每个取值处的概率,其中nl为rs=xl的总数。对求得的pl按照从大到小的顺序排列,记为pl′,对应的关联系数取值为xl′。关联度Rij计算公式为:
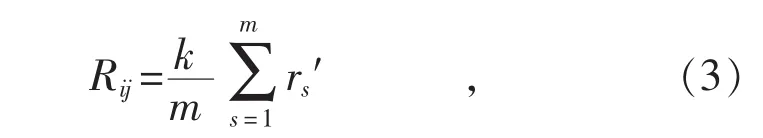
式中:k为分散程度系数,根据统计学经验以及反复的数据分析发现,当随机变量rs在某取值处的概率大于0.7时,可认为rs主要集中分布在该取值处,设a为使得≥0.7的最小取值,当0≤a≤10时 k=1-0.1a, 当 10<a≤15时 k=0; m 为关联系数 rs所有取值为 x0′, …, xa′的总个数; rs′为关联系数 rs中所有取值为 x0′,…,xa′的部分。
根据式(3)计算出关联度 Rij的范围为[0,1],即说明Rij越接近1,关联性越强;越接近0,关联性越弱。通过设定阈值ξ对存在关联的并发异常事件组合进行筛选,当Rij>ξ时,认为2个异常事件存在关联。相关系数与关联性强弱的对应关系[11]如表2所示。

表2 相关系数与关联性强弱的对应关系
根据相关系数与关联性强弱关系将阈值ξ设定为0.4,即认为关联强弱在中等程度及以上的2个异常事件组合有关联。异常事件关联分析流程如图1所示。
3 实例分析
根据第2节方法,基于某市2015年、2016年2年的历史告警数据分别对专变用户和低压用户的两两异常事件组合进行关联分析。为了证明该方法的准确性和可靠性,选取电能表示值不平与电能表飞走、需量超容与反向电量2组异常组合进行关联分析。
3.1 电能表示值不平与电能表飞走
电能表示值不平和电能表飞走这2种异常既面向低压用户又面向专变用户,因此,分别对低压用户和专变进行关联分析。
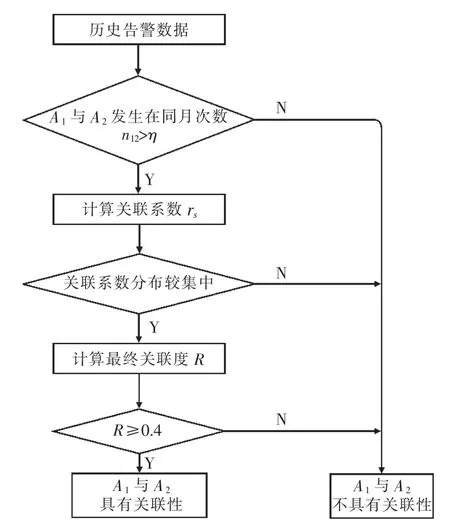
图1 关联分析流程
3.1.1 低压用户电能表示值不平与电能表飞走关联分析
低压用户2年来电能表示值不平与电能表飞走发生的次数如表3所示。

表3 低压用户发生次数统计
(1)初步判断低压用户电能表示值不平与电能表飞走是否具有关联,由式(2)求得:
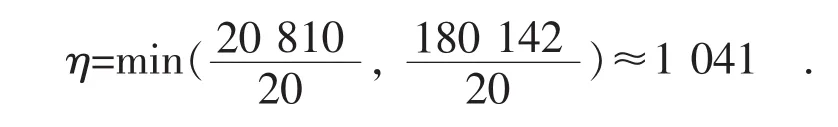
由于η<7 388,因此认为低压用户电能表示值不平与电能表飞走可能存在关联。
(2)关联度计算。 根据式(1)计算出7 388组中每组的关联系数rs(s=1,2,…,7 388),其分布结果如图2所示。
p0′=p1=0.61<0.7, p0′+p1′=p1+p0=0.93>0.7, 所以a=1,k=0.9,rs′为关联系数 rs中所有取值为 x15和x14的部分,最终关联度由式(3)计算得到:
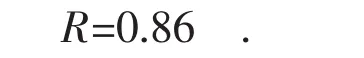
由于R>0.4,因此认为专变用户电能表示值不平与电能表飞走有关联,且属于极强关联。
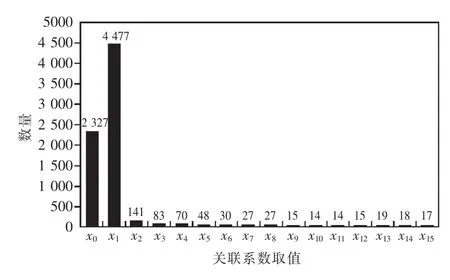
图2 低压用户关联系数分布
3.1.2 专变用户电能表示值不平与电能表飞走关联分析
专变用户2年来电能表示值不平与电能表飞走发生的次数如表4所示。

表4 专变用户发生次数统计
(1)初步判断专变用户电能表示值不平与电能表飞走是否具有关联,由式(2)求得:

由于η<606,因此认为专变用户电能表示值不平与电能表飞走可能存在关联。
(2)关联度计算。根据式(1)计算出606组每组的关联系数大小,关联系数rs(s=1,2,…,606)分布结果如图3所示。
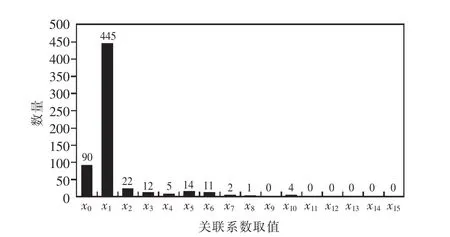
图3 专变用户关联系数分布
p0′=p1=0.73>0.7,所以 a=0, k=1,rs′为关联系数rs中所有取值为x1=0.93的部分,最终关联度由式(3)计算得到:
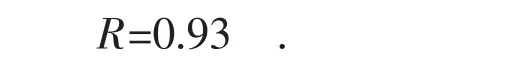
由于R>0.4,因此认为专变用户电能表示值不平与电能表飞走具有关联性,且属于极强关联。
3.1.3 结果分析
电能表示值不平是指电能表总电能示值与各费率电能示值之和不等。引起电能表示值不平的主要原因有采集数据错误、电能表故障和终端故障等;电能表飞走是指电能表日电量明显超过正常值。引起电能表飞走的主要原因有超过合同约定容量用电、电能表故障、终端故障和采集数据错误等。电能表示值不平和电能表飞走都属于电量异常,二者均可由采集数据错误、电能表故障和终端故障引发。因此,可以认为电能表示值不平和电能表飞走之间具有较高的关联。由本文提出的关联算法求出的低压用户关联度为0.86、专变用户关联度为0.93,均大于0.80,属于极强关联,说明该关联算法求出的关联度值与实际结果相符合。
3.2 需量超容与反向电量异常关联分析
由于需量超容只面向专变用户,此处对专变用户进行关联分析。2年来专变用户需量超容与反向电量异常发生的次数如表5所示。

表5 专变用户发生次数统计
(1)初步判断需量超容与反向电量异常是否有关联,由式(2)求得:
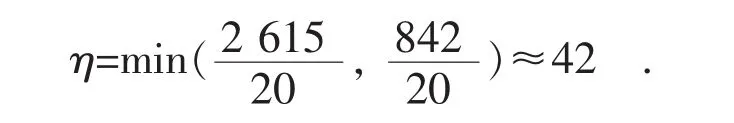
因为η>10,所以认为需量超容与反向电量异常无关联。
(2)结果分析。需量超容是指按最大需量计算基本电费的专变用户,电能表记录的最大需量超出用户合同。引起需量超容的主要原因为需量算费用户用电负荷过大,超过用户合同约定需量;反向电量异常是指非发电用户电能表反向有功总示值大于0,且每日反向有功总示值有一定增量。引起反向电量异常的原因主要有:计量回路接线错误、电能表故障、用户负荷特性和载波信号干扰等。需量超容属于负荷异常;反向电量异常属于接线异常。二者无论是异常属性还是引发异常的原因都无相同之处,理论上可以认为需量超容与反向电量异常无关联,与本文提出的关联算法求出的结果一致。
4 结语
经过实例分析证明,本文提出的基于异常发生日期间隔天数的关联度算法,能够简捷准确地计算出两两异常事件之间的关联度。设置适当的关联度阈值能有效地甄别和筛选出具有关联的并发计量异常事件组合,为后续有效地利用异常告警数据对异常原因和异常用电行为进行分析诊断奠定了基础。

