爆破荷载作用下浅埋高压管道的应力变化规律

(1.中铁港航-武汉科技大学爆破技术研究中心 湖北 武汉 430065；2.武汉科技大学 理学院 湖北 武汉 430065)

引言

地下管线系统是现代经济建设与发展中不可缺少的一部分，随着城市规模的日益扩张与经济需求的快速增长，地下管网的作用愈加明显，其安全运行得到了各部门的重视。随着国家基础设施建设规模的增长，原有地下管道附近进行爆破施工的情况时有发生，而爆破产生的冲击波、地震波等有害因素就有可能危害到管道安全，因此，为确保施工过程中地下管网的安全，爆破振动下埋地管道的动力响应以及应力应变变化的规律研究成为爆破安全领域的热点。近年来，国内外学者进行了相应的研究，取得了不少成果。张黎明[1]基于管道破坏的应变准则，利用相关的测试系统对工程爆破进行现场监测，建立了爆破振动质点峰值速度与管道破坏的对应关系。张紫剑等[2]利用相关测试仪对现场埋地管道的爆破振动和管道应变进行监控，得出不同频率段的相关参数和萨氏公式有所不同，指出在实际施工过程中应结合具体情况确定爆破方案。房冲[3]等利用ANSYS/LS-DYNA对内空和充水管道在空爆下的管道动力响应情况进行了模拟对比，发现在等量炸药下充水管道的形变量、单元位移和单元压强峰值都低于内空管道。有许多学者[4-6]运用LSDYNA3D方法对下穿隧道掘进爆破时埋地管道响应规律进行模拟，发现管道壁厚减小或管道直径增加会引起管道动应力增大，管道动力响应随埋深增大显著降低。马东方[7]等人从动态、静态两个角度考虑，在爆破压力下以及地震波的作用下，讨论埋地管道的响应，在地下管道中，相对于环向位移，其径向的位移响应要大的多，管道的在沿着径向的位移的幅值较大，而环向的则较小。刘学通[8]等人对爆破振动下埋地管道动力响应研究进展进行了归纳和总结，并提出了今后对管道动力响应研究的主要方向和方法。刘建民[9]通过实验对比分析了炸药布置方式以及炸药与管线相对位置对管线动力响应的影响。陈艳华等[10]结合液固耦合及天然地震荷载作用，探究了埋地管内不同运送液体密度及不同流量等因素对管道破坏的情况，得出油气密度与管道破坏程度呈正比，油气流速越快，破坏越严重。刘志伟[11]结合工程实际对施工时重型构件发生坠落对下方埋地高压管道的动力响应情况进行了研究，提出了明确的管道保护措施。Abedi A S[12]等人将爆炸下管道模型简化为两端固定梁模型，建立四阶非齐次偏微分方程，利用Fourier变换将时域问题变化为频域问题解出偏微分方程，求得管道在爆炸波作用下的挠度。

但实际工程中，对于爆破振动对埋地内压较高的高压管道的影响研究还较少，由于高压管道在爆破扰动下的受载情况更加复杂，现有的经典理论解决高压埋地管道的爆破动力响应问题比较困难，而相关实验研究消耗巨大且难以实施。LS-DYNA作为国际上广泛运用的有限元分析软件，兼具线性、非线性以及动力学、流固耦合计算功能，其解决实际工程问题的能力得到广泛认可，基于此类有限元工具对高压埋地管道的爆破动力响应问题进行数值模拟分析是较高效的手段。鉴于此，本文借助LS-DYNA，采用动力松弛法对管道内压进行初始化，结合流固耦合算法模拟管道、土壤、罐内气体以及炸药之间的相互作用，研究浅爆破荷载作用下埋高压管线的动力响应，分析管道的应力应变规律，以期为建立完善的管道近区爆破施工规范提供一定的参考依据。

一、理论分析

(一)管壁环向应力和径向应力

高压埋地管道可以近似看作受均布压力作用的圆筒，如图1所示，设圆筒内半径为r，外半径为R。在爆炸波传来之前，管道内压为q1，外部压力(土压力)为q2。

若在极坐标下系下的径向坐标和周向坐标分别用ρ和θ表示，根据弹性力学基本原理，可以求得该问题的拉梅解答[13]如下：

(1)

由式(1)可知：当外压为0，管道内压单独作用下的σρ总是压应力，σθ总是拉应力；当内压为0，外压单独作用下的σρ和σθ都是压应力。可以推断，由于内外压对管壁的作用方向相反，二者叠加后会使管壁上σρ增大，而σθ减小。

土壤传来的爆炸压力q3作用在管壁外部，是外压，如图2，因爆炸应力波并非均匀作用在管道外壁，其对管道应力的影响比较复杂，可以用以下函数表示爆炸压力作用下的管道应力：

(2)

将(1)、(2)叠加即为爆破荷载作用下高压埋地管道管壁环向和径向应力：

(3)

图1 管壁受均布内外压

图2 爆破荷载作用下的埋地高压管道截面

(二)管壁轴向应力计算

假设管线水平方向分析模型如图3所示，沿管线长度X方向的抗弯刚度为EI(z)，单位长度的质量为m(z)，作用在管上的横向爆破荷载为q3(z，t)。

图3 爆破荷载作用下高压管道与土体作用

建立管道的弯曲积分方程为：

(4)

梁弯曲的最大弯曲正应力计算公式为：

(5)

式中W为管道抗弯截面系数，空心圆柱结构的抗弯截面系数为：

(6)

钢管在工程中主要表现为塑性屈服，常采用Mises屈服准则[14]。一般在不受扭矩情况下，钢制管壁上的主应力即为σρ、σθ、σz，则Mises等效应力为：

(7)

二、数值模拟

(一)模型建立

为了探究浅埋高压管道在不同爆破位置爆炸对管道的影响，按照图4所示的管线区域横截面建立简化模型。计算中涉及到炸药、土壤、管道和空气四者之间的相互作用，管道埋深为2m。管道尺寸[15]：外径0.3m，内径0.28m。根据文献[9]和文献[16]的研究内容，设计1#～6#六种炸药布置工况，装药量均为1000g，其中1#～3#炸药与管线中心水平距离分别为5m、3m、1m，4#～6#炸药与管线中心垂直距离分别是1m、1.5m、2m，并且6#炸药放置在地面。数值模拟中，取5m长管段建立三维模型，土体域为6m×5m×3m，空气域在土体上方，高度0.5m。土体、空气和炸药采用ALE算法，用SOLID164单元划分成六面体网格，管道采用LAGRANGE算法，用SHELL163单元划分成四边形网格。兼顾模拟精度和计算效率，通过试算确定网格尺寸控制在0.05m。最终建立的有限元模型如图5所示，一共划分了747100个单元。

图4 埋地管线区域示意图

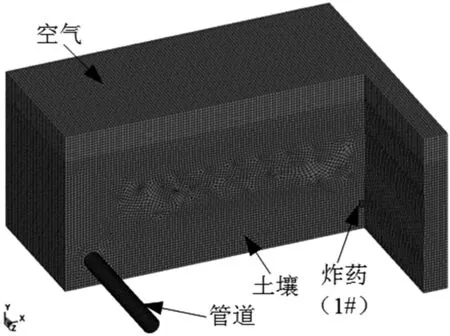
图5 有限元模型

1.边界条件

实际工程中，管线一般较长，并且爆炸应力波及地震波在泥土中的传播距离也较大，为了更接近工程实际，将模型边界均设置为无反射边界条件。管道壁、管道内气体以及炸药之间的相互关系通过流固耦合关键字定义，采用罚函数的方式耦合各物质之间的物理量。管道和泥土的相互作用也采用多物质耦合算法实现。

2.材料模型及参数

(1)管道材料本构模型

管道材料为高强度钢材，采用双线性随动硬化弹塑性本构模型模拟，密度为7850 kg/m3，泊松比为0.3，初始弹性模量为2.1×1011Pa，屈服应力为400 MPa，切线模量为5.0×108Pa。

(2)土壤材料模型及参数

土壤采用泡沫材料模型模拟，其基本物理参数如下：密度为1800kg/m3，剪切模量为1.601×107Pa泊松比为0.48，体积压缩模量为1.328×1012Pa。

(3)炸药模型及状态方程

炸药采用LS-DYNA自带的高能炸药模型模拟，采用JWL状态方程进行爆轰压力计算：

(8)

式中：P为爆轰压力；E为炸药爆轰产物的内能；V为爆轰产物的相对体积；A，B，R1，R2，ω—所选炸药的性质常数。选取的炸药材料及状态方程参数如下表所示。

表1 炸药材料及状态方程参数

(4)空气材料模型及状态方程

空气采用LS-DYNA中的NULL流体材料模型。空气单元压力采用线性多项式状态方程模拟：

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(9)

空气状态方程种各系数取值如下：C0=-1×105，C1=C2=C3=C6==0，C4=C5=0.4，E0= 3×105，V0=1.0。

(二)管道内压初始化

高压埋地管道的内压是进行管道安全性设计不可忽略的因素。在进行浅埋高压管道爆破动力响应的数值模拟时，应充分考虑管道在内压作用下的初始应力静平衡状态。LS-DYNA的显式求解能力处理爆炸与冲击、结构碰撞、金属加工成型等高度非线性的瞬态动力学问题是非常有效，但是在处理静力学问题时，由于显式求解器的特点，无法得到稳定的结果，而需要运用动力松弛的方式对静态或者准静态问题进行近似求解。动力松弛法是从空间和时间两方面将结构体系离散化。空间上的离散化是将结构体系离散为单元和结点，并假定其质量集中于结点上。如果在结点上施加激振力，结点将产生振动，由于阻尼的存在，振动将逐步减弱，最终达到静力平衡。计算中程序通过增加阻尼使结构动能逐步降低，求解器每隔一定的循环次数检查动能状态直到为0。本文采用这种方法对管道在内压作用下的应力状态进行初始化。根据规范[15]设计管道在内压为10MPa的情况下，管壁第一主应力的初始化结果为146MPa，理论结果为140MPa，误差不超过0.05。

(三)计算结果分析

1.管道的应力变化规律

为了探究爆破荷载作用下管道壁的Mises应力变化情况，如图6所示，在管道模型上正对爆心截面选取四个单元考察应力沿管壁环向分布，并且在迎爆面沿轴向选取四个单元考察应力沿管壁轴向分布。输出各工况下管壁不同位置的应力曲线如图7和图8。

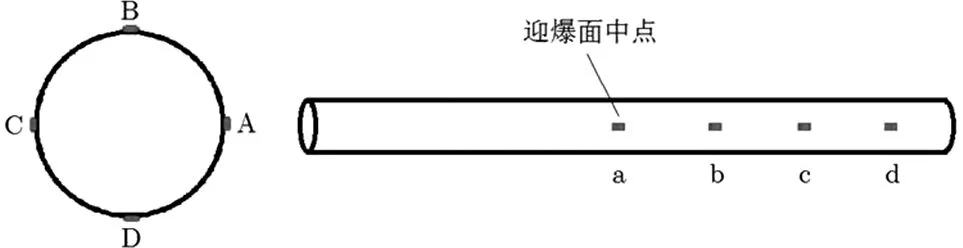
图6 考察单元位置

(1)应力沿管壁环向分布

图7 各工况下管壁环向不同位置的应力曲线

(2)应力沿管壁轴向分布

图8 各工况下管壁轴向不同位置的应力曲线

由以上应力曲线可以看出，1#、2#、5#、6#四种工况在爆炸荷载作用下，管壁Mises应力较初始应力均有所减小。由前面的理论分析可知，这几种工况下爆源距离管道较远，管道挠度较小，管壁产生的轴向应力也很小，而爆炸荷载与管道内压对管壁的作用方向相反，使管壁环向应力减小，所以最终Mises应力减小。而3#、4#工况爆源距离管壁较近，作用在管壁上的爆炸荷载较大，管道挠度较大从而使管壁产生很大的轴向应力，最终Mises应力增大。并且爆源距离较远时，爆炸荷载对管道的作用较为均匀，管壁各处Mises应力曲线基本一致。

分析图6中3#和4#工况下的应变曲线可以发现：3#工况下应变曲线出现的的第一个峰值最大位置是C点，第二个峰值最大位置是A点；4#工况下应变曲线出现的的第一个峰值最大位置是D点，第二个峰值最大位置是B点。其中A点和C点分别是工况3#和4#下正对爆源的位置，B点和D点分别是工况3#和4#下背对爆源的位置，当爆炸波传来时，管道向爆炸波传播方向弯曲，此时背对爆源的位置首先受拉，轴向拉应力急剧增大，所以第一个最大峰值出现在背对爆源位置；随着爆炸波离去，管道在自身弹性力作用下恢复并在惯性作用下向正对爆源方向弯曲，此时正对爆源位置受拉，轴向应力急剧增大，所以第二个最大峰值出现在正对爆源位置。

2.管道的破坏形态

在装药量为1000g的情况下，1#～6#炸药布置方式均未使管道发生破坏，说明这些工况下管道是安全的。但是，当药量增大或者炸药距离减小时，管道仍有可能因应力超过强度极限而发生塑性屈服。将3#工况药量增十倍，管道的破坏过程如图9所示。爆炸波传到管道处时，管道正对爆源的位置首先发生屈服，随后向后及两端扩展，越靠近爆源的位置局部破坏越严重。

图9 管道破坏过程

三、结论

根据弹性力学基本原理将埋地管道简化成圆筒受压力模型和弹简支梁模型，建立了爆破荷载作用下浅埋高压管道管壁环向应力、径向应力和轴向应力的理论表达式。并运用LS-DYNA计算了不同工况爆炸荷载作用下管壁应力变化规律，可以初步得到以下结论：

(1)LS-DYNA的动力松弛法能有效对浅埋高压管道进行应力初始化，内压10MPa情况下的初始化结果与理论结果之间误差不超过0.05。并且流固耦合算法能有效模拟爆炸荷载对管道的影响。

(2)在小药量、远距离爆炸荷载作用下，管道所产生的挠度比较小，轴向弯曲正应力很小，此时管壁主要是环向应力，而爆炸荷载和管道内压的作用方向相反，对管壁环向应力的影响相反，因此，爆炸荷载作用下管壁Mises应力会略有减小。当距离减小或者药量增大时，管道挠度增大，轴向弯曲正应力较大，此时管壁轴向应力占主导地位，虽然爆炸荷载作用下环向应力有所减小，但是Mises应力仍会增大。

(3)爆炸荷载对管道迎爆侧正对爆源的位置影响最为显著，总体呈现出从正面到背面逐渐减小、从正对爆源处到远离爆源处逐渐减小的趋势。

(4)爆炸荷载作用下浅埋高压管道的破坏原因是管道挠度过大，管壁轴向应力增大，导致管道正对爆源位置应力超过强度极限而发生塑性屈服。算例中管道中部破坏情况最为严重。