应用Canny算子的织物疵点检测改进算法
胡克满, 罗少龙, 胡海燕
(1. 宁波职业技术学院 电子信息工程学院, 浙江 宁波 315800; 2. 澳门科技大学 资讯科技学院, 澳门 999078;3. 宁波职业技术学院 科技与产学合作处, 浙江 宁波 315800)
纺织品在生产过程中,由于纱线的质量问题或其他原因导致织物出现不同程度的疵点。如果未能严格把控胚布的生产质量,织物疵点将给二次加工、深加工等流程造成不必要的经济损失,因此,织物的表观质量检测是企业生产质量控制的关键技术之一。目前不少小微型企业对织物疵点的检测主要依靠人工作业,而人工作业容易受到外界因素的影响,对工人的技术与经验要求高,也是一项需要精力高度集中的工作岗位,工人容易疲劳,且人工成本较高[1]。随着人工智能、图形图像处理等技术的不断发展,采用机器视觉替代人工进行织物疵点识别已成为众多企业的优先选择与迫切需求。
近年来国内外专家学者基于计算机视觉技术及图形图像处理技术对织物疵点检测方法展开探讨,并取得不少研究成果。目前织物疵点检测主要研究方法可分为4大类:基于模型研究方法,基于数学统计研究方法,基于频谱分析研究方法和基于结构研究方法[2-3]。基于模型研究方法,即构建某种参数化数学模型,但是这种模型计算量大,对于相对隐蔽的较小面积的织物疵点的识别能力较弱[4];基于数学统计研究方法,主要是对检测织物的图像特征进行统计分析,由于统计方法的不一样使得结果不同,其自适应性较弱[5];基于频谱分析研究方法,目前主要采用Gabor变化、傅里叶变化等,该方法对滤波器的要求较高,检测效果很大程度上依赖于滤波器的选择,因此滤波器的选择与优化起到决定性的作用[6];基于结构的研究方法,运用了结构形态学的方法识别织物疵点信息,由于织物结构的多样性使得该方法的应用过程带了一定的困难[7]。
由于织物疵点图像边缘包含了丰富的信息量,如不同疵点、背景与疵点、疵点与疵点之间等信息,在织物疵点检测中引入边缘检测技术是十分有效的方法。目前较为常用的边缘检测算子有Prewitt算子、Roberts算子、Laplacian算子等[8],较上述边缘检测算子想比较,Canny算子边缘检测具有检测精度高、信噪比大等特点,在图像识别技术中得到广泛的应用,Canny算子检测属于基于频谱分析研究方法,而Canny算法阈值的选择相对被动需要人工设定,从而影响其实时性和自适应性[9-10]。本文基于现有Canny算法对其进行分析,并提出一种自适应改进的Canny边缘检测算法。选择高斯滤波器针对不同疵点种类设计多个高斯滤波参数,较好地实现了去除噪声并保留了更多的边缘信息,可根据织物图像特征自适应确定Canny算子阈值。由于无需人工设定阈值,大大改善了Canny自适应性,可较好地检测出织物疵点图像的边缘信息,准确地识别织物疵点。
1 Canny算法的疵点检测原理分析
John Canny于1986年提出一种边缘检测算法,并基于3个准则以达到较好的边缘检测目的,即信噪比准则、定位准则、单边响应准则[11]。对于织物疵点检测图像信息的处理,需要有较好的信噪比,准确的疵点定位以及虚假边缘抑制等特征要求,因此本文提出利用Canny算法进行织物疵点检测。
1.1 Canny算法的疵点检测主要步骤
第1步,高斯滤波消除噪声。利用二维高斯滤波对被检测图像进行滤波处理,高斯函数滤波参数δ通过人工设定,从而达到降噪获得平滑图像。
(1)
根据织物疵点的类型不同选择高斯函数滤波参数δ,经试验证明高斯滤波参数δ对于不同种类的织物疵点滤波器设置敏感。为了更好地说明问题,以纬纱带入这类织物疵点为说明对象。选取高斯滤波参数δ为1,构建纬纱带入检测滤波器如图1所示,滤波器矩阵G见下。

图1 高斯滤波器Fig.1 Gauss filter. (a) 3-D of Gauss filter;(b) 2D of Gauss filter

经滤波后得到的纬纱带入检测信息如图2所示。

图2 滤波处理图Fig.2 Image processed by filter. (a)Original image;(b) Filtered image
从图2中可发现滤处理后的图片与原图片之间的差异,原图为色彩饱满的图片,经过滤波后获得了二值化图片,滤波处理图片是为了获得边缘信息重要环节之一。
第2步,计算梯度向量与梯度幅值。对通过高斯滤波后的图像进行计算梯度向量与梯度幅值,设梯度向量为θ(x,y),梯度幅值为H(x,y)。利用一阶差分算子分别进行水平方向的梯度幅值分量Gx和垂直方向的梯度分量Gy的运算求值,图3、4分别为水平和垂直方向的梯度分量的能量分布图。根据水平方向的梯度幅值分量Gx和垂直方向的梯度分量Gy可求得梯度向量为θ(x,y)和梯度幅值为H(x,y),如式(2)、(3)所示。
(2)
(3)
通常θ(x,y)梯度向量所取的角度为0°~180°之间的45°的倍数,即
θ(x,y)=n·45°,n=0,1,2,3
(4)
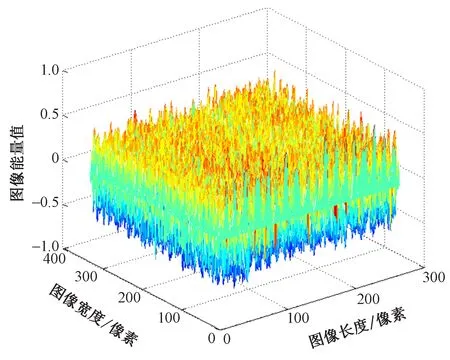
图3 水平方向能量响应值Fig.3 X-Direction of energy estimates
第3步,极大值的选择与非极大值的抑制。通过对极大值的选择与非极大值的抑制,去除一些非边缘信息,尽可能排除干扰信息,并保留相对较优信息作为边缘信息,这样可以使得织物疵点的边缘信息更加凸显。
第4步,阈值选择。确定高阈值与低阈值,通常高于阈值信息将被保留,并被确认为边缘信息,而低于阈值信息被剔除,形成滞后阈值现象。阈值大小的确定与选择直接影响边缘信息,对获得检测边缘的质量起到关键性的作用。而确定阈值通常是需要根据多次实验结果,从而由人工选取相对较为理想的值。
1.2 Canny算法疵点检测过程关键技术分析
1)传统的Canny算法依赖于高斯滤波对原图进行平滑滤波与去噪,其中由式(4)可以发现δ为高斯函数滤波参数,参数值δ的选择将影响原图的滤波与平滑效果。而参数值δ的选择是由人工设定,这也使得传统Canny算法针对不同的图像需要人工选择不同的参数值δ,很大程度上影响了其性能的发挥。根据对织物疵点检测过程的分析,本文将高斯函数滤波参数δ针对不同种类疵点进行适当的调整,其检测效果更佳理想。
2)传统Canny算法在进行边缘检测前先人工设定高阈值和低阈值。而设定相同的高阈值和低阈值对处理不同的图像,也同样使得边缘检测效果不尽相同。而在织物疵点检测过程中,往往可根据织物疵点种类的判断提前选取相应的高斯函数滤波参数值δ,但是对阈值的选择一方面需要大量实验,另一方面也需要经验值判断,因此,如何通过自适应方式获得图像自身所需的阈值是提高传统Canny算法性能的有效途径之一。
本文针对上述基于Canny算子织物检测过程关键技术分析,提出一种自适应获得阈值的方法并对传统Canny算法的进行改进,通过实验验证获得了良好的效果。
2 疵点检测算法的优化
在织物疵点检测过程中,由于织物疵点的种类繁多,不同种类的疵点采用不同的滤波器,其检测效果更加有效。滤波参数的选择是构建滤波器重要的关键点之一,针对传统Canny算法的滤波参数选择与高阈值和低阈值选择的不足之处,本文对其进行改进。
2.1 自适应滤波去噪
在织物疵点检测过程中,选择不同的滤波器目的是为了能够适应不同的织物疵点特征的检测。为能够更好地设计自适应滤波器,其基本思想为局部加权和原图信号迭代卷积,每次迭代都会改变加权系数,从而逐步形成自适应性。在迭代过程中锐化了区域边缘,也使得区域内部得到平滑。自适应迭代的过程是逐步进行的,需要经过多次迭代得到,具体步骤如下。
1)设定迭代次数,根据文献[9]所分析的迭代次数结果,本文迭代次数采用二分法查找进行实验,估算并设定一个相对较大的值,记录每次实验的结果,并将本次实验结果与上次实验结构进行比较,根据比较结果判断收敛方向。在实验中通过二分法查法可以较好获得收敛点,但是值得注意的是由于本文所获得的收敛点为迭代次数,是离散的数据,所以在实际实验过程中应选取最接近收敛点的离散数值,通常这个时候选取的数值与个人偏好及工程经验有一定的关系。结合实际实验总结设迭代最大值K=5,并令k=0,参数h的设定见文献[12]。
2)分别计算梯度向量Gx(x,y)和Gy(x,y):
(5)
(6)
3)确定滤波器的权系数:
(7)
4)对f(k)(x,y)加权平均:
f(k+1)(x,y)=
(8)
5)判断迭代是否结束,当k≤K则继续步骤2),直到k>K时迭代完成。
2.2 自适应阈值选择
对织物疵点进行检测时,当滤波器确定后,Canny阈值在图像处理前需要人工设定,而这种设定通常需要做大量的试验和经验判断织物疵点检测效果,由此带来的不便。在织物疵点图像处理过程中高阈值的大小反映边缘信息的保留量。过高的阈值很难获得足够多的边缘信息,容易丢失边缘信息[13];过低的阈值又导致边缘信息冗余,使得非边缘信息冗余无法较好的呈现真实边缘信息,高阈值的选择应考虑织物疵点图像的整体情况,根据上述分析,局部方差的变化反映局部图像的变化情况,为了能够获得织物疵点图像的整体效果,取图像的平均方差和平均灰度作为图像的高阈值参数。获取高阈值的方法如下:令Eave为图像平均方差,Fave为图像平均灰度,Lw为图像的宽度,Lh为图像的高度,Th为高阈值,Tl为低阈值。
(9)
(10)
(11)
Tl=μTh
(12)
经过多次实验测试,对不同的织物疵点图像进行测试,其中μ∈[0.25,0.5]效果较好。本文实验测试选取μ=0.5。
3 实验结果与讨论
为验证本文算法的有效性和可行性,更好地检验效果,实验在Linux操作系统下配置OpenCV3.0.1实验环境,算法代码采用MatLab和Python语言编写。本文选取漏纱、跳花、破损、纬松、结头等典型的织物疵点图像进行实验。
为对常见的几种织物疵点吊经、松经、浮经、纬纱带入、重经等,利用传统的Canny算法进行处理,对传统的Canny算法进行高、低阈值与高斯函数滤波参数δ的设定。设置高阈值为400,低阈值为200,高斯函数滤波参数δ为3,结果如图5所示。可看出检测到边缘信息较少,不能完整地反映吊经、松经、浮经、纬纱带入等织物疵点的边缘信息。设置高阈值为50,低阈值为25,高斯函数滤波参数δ为3,结果如图6所示。结果显示检测到边缘信息冗余。在高斯函数滤波参数δ取值一定的情况下阈值的选择非常重要,过高无法完整的表达边缘信息,过低使得边缘信息冗余,也同样无法较好的反应真实边缘情况。图7示出本算法通过自适应方式获得参数值的实验结果,可以看出,获得了较好的边缘信息,织物疵点可有效地被识别。

图5 高阈值400检测结果Fig.5 Result of high threshold value 400.(a)Tight warp;(b)Loose warp;(c) Floating selvedge;(d)Result of tight warp; (e)Result of loose warp; (f)Result of floating selvedge

图6 高阈值50检测结果Fig.6 Result of high threshold value 50.(a)Tight warp; (b)Loose warp; (c) Floating selvedge;(d)Result of tight warp; (e)Result of loose warp; (f)Result of floating selvedge

图7 本文算法结果Fig.7 Algorithm result of the paper. (a)Original image;(b)Gray image; (c) Image binarization; (d)Result of original image
由此可见,通过自适应形式获得滤波参数及高阈值和低阈值时,其图像检测效果与通过人工设定的值相比更加有效,同时也避免了由于经验不足而造成的对高阈值和低阈值设定的不确定性。与传统的Canny算法相比,改进的算法对织物疵点的检测效果要优于传统的Canny算法。
为进一步验证本文算法的有效性,通过对不同类型的疵点图像进行实验检测,结果表明改进的算法可有效地检测出织物疵点。
输入包含疵点的图像共70张包括吊经、松经、浮经、破洞、油脂污染和星跳等不同类型的疵点图像,无疵点的图像20张。本文算法可有效地检测出疵点图片为66张,其中对检测破洞效果最佳,其次浮经、吊经、油脂污染检测效果尚可,次之为松经和断头。另有3张星跳和1张断头边缘不太明显的图像未能被有效地检测。无疵点图像共20张,均可有效地被检测。
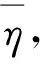
(13)
误检率为
(14)
研究发现,本文算法在检测过程中,对包含织物疵点的图片进行处理仍然存在没有被检测出来的情况,其中主要原因在于Canny算子本身特性的局限导致其无法检测的结果,Canny算子主要是对图像的边缘信息提取进行检测,而织物疵点的种类繁多,其中部分织物疵点的边缘信息特征表现不明显时,Canny算法就无法对其进行边缘信息提取。例如该算法对织物疵点星跳的检测相对其他种类的织物疵点正检测率要低,其主要原因是由于星跳疵点边缘不显著,从而导致该类织物疵点的正检率偏低,因此,在针对类似于星跳疵点的织物疵点检测,应该通过多次实验,从而构造滤波器及阈值的设定,这样可以有效地提高该类检测效果。
4 结束语
本文在传统的Canny算法的基础上,提出一种改进的织物检测算法,深入地探讨了传统Canny算法的工作原理并对其关键技术进行了分析。针对传统Canny算法的不足设计了自适应Canny算法,并应用于织物疵点检测。
传统的Canny算法对阈值的设定过高导致织物疵点边缘信息不足,过低使得边缘信息冗余。本文算法利用自适应方法获得阈值与高斯函数滤波参数δ,能够有效地检测出织物疵点的边缘信息,同时也可以应用于其他领域的图像识别技术,具有一定的实际应用价值。
FZXB

