“两角差的余弦公式”的教学探究
张金环
(江苏省东海高级中学,江苏 东海)
两角差的余弦公式的教学在三角恒等变换中是开头一节,本节课的教学,对于后面的两角和的余弦以及两角和与差的正弦公式都有很强的引领作用,开启了利用向量方法研究角度问题的先例,在三角恒等变换一章中占有很重要的地位;同时,由于本节课特殊的教学视角,在省、市举行的基本功比赛中,这节课经常作为比赛课题,本人就这节课面对全组数学教师上了一节公开课,觉得还有很多要探究的地方,于是,我又查阅了中数参考文献[1][2][3],加上自己教学中的一些感悟,谈几点对本节课的看法.
两角差的余弦公式是一节概念公式探究课,探究的重点是公式的推导.课本上给出了推导两角差的余弦公式的两种方法:一是用三角形全等和距离公式来构造三角恒等关系式.如图
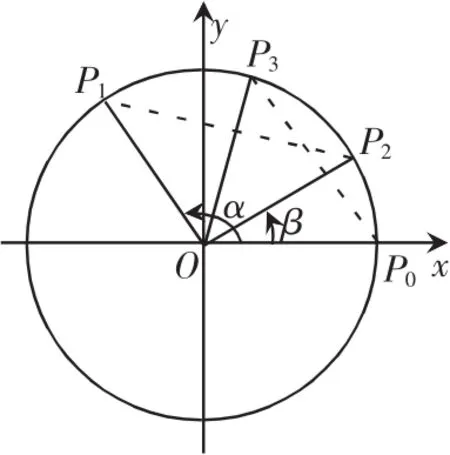
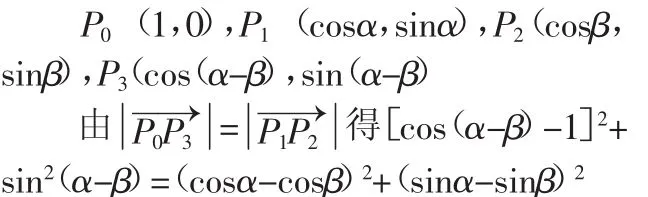
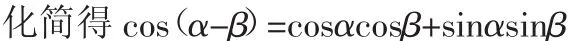
另一种方法是利用向量的数量积来推导,步骤如下:
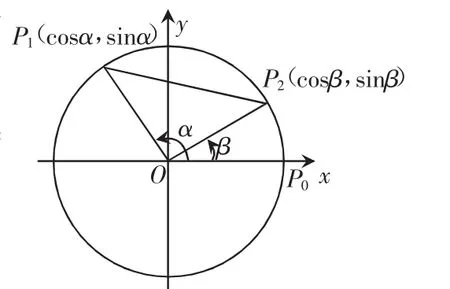
在直角坐标系中,以x轴为始边作α,β角,其终边分别为射线OP1,OP2,其中P1(cosα,sinα),P2(cosβ,sinβ)分别为其终边与单位圆的交点,则∠P1OP2=α-β.
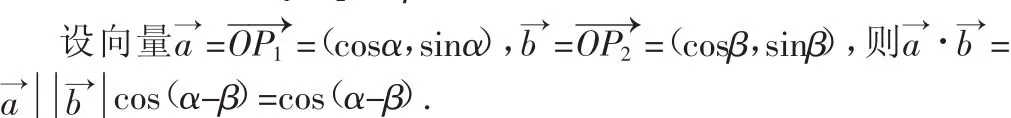
应该说,无论是距离公式法还是向量法学生都很难想到,有的学生就在课堂上提出疑问:怎么想到用距离相等来证明的?我怎么看不出有的学生虽然没有直接提出问题,从他们困惑的眼神可以看出学生的茫然,而且这种方法里涉及的α,β,α-β角的范围还是在[0,π]内,教材上也没有对这个问题作详细的说明,而这与高中阶段将角度推广到任意角的思想是不符合的,因此以上思想可以作为备用方法,在公式推导完后由教师指导学生完成以上证明.而利用向量法来证明两角差的余弦公式,也是很突兀的,就像是魔术师的帽子里突然跳出一只兔子.因此,教学中的情景引入很重要,启发学生的思维,让他们一步步地意识到可以利用向量数量积来研究向量的夹角问题.好在学生刚刚学完向量,对基础知识还比较熟悉,知识储备很完善,具体可以从以下几个方面去拓展教学.
1.如何让学生想到利用向量法推导公式
教学时,遵循从特殊到一般的原则,先证明α-β∈[0,π]时的情形,可以先提出几个问题作为铺垫:
(1)如何在坐标系中放置α,β角?
(2)已知 α,β 的三角函数值求 cos(α-β)时,α-β 可以看成什么角?
(3)前面学习的哪个知识点涉及夹角问题?
文[1][2][3]对这个问题都进行了探讨,其中文[1]认为不必过多讨论,[2][3]持赞同意见,在这里不一一赘述.需不需要进行探究,可以放到课堂上检验.当我讲解了α-β∈[0,π]的情形得到两角差的余弦公式后,有学生提出疑问:老师,当α-β∈[π,2π]时该怎么办?我说你觉得呢?他思考了一下说可以考虑利用三角函数的周期性减去一个周期2π.马上又有学生提出来:减一个周期 2π,α-β∈[-π,0],还不在的范围内,怎么办?看来,这个问题不解决,学生在这节课上所得到的只能是对公式的死记硬背,更不要提对公式的活学活用了.
3.当 α-β∉[0,π]时公式的证明
文[1]中对α-β∈[0,π]的情形已作了证明,在这里就不赘述了.
下面讨论 α-β∈[π,2π],则 α-β-π∈[0,π],此时 cos(α-βπ)=-cos(α-β)
另一方面,cos(α-β-π)中的 α-β-π∈[0,π]可以利用两角和与差的余弦公式展开:cos(α-β-π)=cos(α-π)cosβ+sin(α-π)sinβ=-cosαcosβ-sinαsinβ

4.有没有其他方法证明?
利用余弦定理、两点间距离证明.

以上是两角差的余弦公式一节需要探究的几个点,本节课的关键是如何通过已学的知识,如三角函数的定义,平面向量的数量积,余弦定理等,通过解析法,把几个条件通过恰当的推导,得到余弦公式的过程.对于文中提到的1、2、3、4几个问题,可以作为本节的拓展内容,对学生来讲既是一种知识的升华,又提供给学生宽广的探索空间.可以说,只有顺利地解决了以上几个问题,才能让学生真正有所悟,从而收到好的教学效果.美国心理学家布鲁纳说“探索是数学的生命线”.一堂概念公式探究课,教师在充分备课的基础上,以学生自主探究活动为主线,教师精讲点拨为辅线,真正让学生体会到如何探究,以培养学生的创造性思维能力,提高数学素养,并在探究的过程中,获得自己独有的情感体验.这样的课堂,才是真实的,才具有生命力,让我们共同为这样的数学课堂而努力吧!

