整体代入求值五例

陆敬雨

（江苏省宿迁市宿豫区陆集中学，江苏 宿迁）

整体思想是数学教学中的一种重要的数学思想。整体代入可以解决一些复杂的代入求值问题。整体代入求值大致可分为，直接整体代入、取相反数之后整体代入、变形后整体代入、多次整体代入和幂的运算有关的整体带入等几种常见情况。

一、直接整体代入

这种情况是指一些比较简单的代入求值问题，对已知条件不需要处理便可以直接代入计算。

例如：已知x-y=7，求代数式x-y-3的值。

解析：此题只要把x-y当做整体即可。即：x-y-3=7-3=4

二、取相反数后整体代入

这种题型是表面上看起来已知条件和要求值的代数式没有明显关系，其实是已知条件和代数式的部分项是互为相反数关系。

例如：已知x-y=7，求代数式3-x+y的值。

解析：从题目上看出x-y与-x+y互为相反数。

因为x－y=7

所以－x+y=－7

所以原式=3－7=－4

三、变形后整体代入

这种题型虽然比上面两种情况稍复杂一些，但是利用等式性质对已知条件进行一些简单变形后就可以整体代入顺利求出原代数式的值。

例1.已知4x2-2y+5=7，求2x2-y+1的值。

解析：由4x2-2y+5=7两边同时减5可得：4x2-2y=2

两边同时除以2得：2x2-y=1

把2x2-y=1整体代入得：2x2-y+1=1+1=2

两边同时乘以xy得：y-x=3xy

两边同时乘-1得：x-y=-3xy

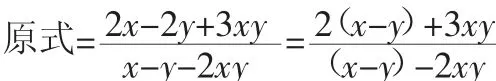
把x-y=-3xy作为整体代入得：

四、变形后多次整体代入

这种题型表面上看，已知条件和所要求值的代数式没有明显的关系，只要我们仔细观察，对已知条件和所要求值的代数式适当变形，就可以发现它们之间的关系。

例1.已知x2+x-1=0，求x3+2x2+2013的值。

解析：因为x2+x-1=0

所以x3+x2-x=0

所以x3+x2=x

所以x3+2x2+2013=x3+x2+x2+2013

把x3+x2=x整体代入得：

原式=x+x2+2013

又因为x2+x-1=0

所以x2+x=1

例 2.已知a-b=2，b-c=1，求a（a-b）-2c（b-c）的值。

解析：因为a-b=2，b-c=1

所以a-c=3

所以a（a-b）-2c（b-c）=2a-2c=2（a-c）=2×3=6

五、与幂的运算有关的整体带入

这种类型的题目是通过同底数幂相乘法、幂的乘方、积的乘方、同底数幂相除等相关知识的灵活运用对代数式进行变形后再进行整体带入。

例 1.若am=8，an=16，则am+n=______

解析：这是一个同底数幂相乘的逆运用am+n=am·an，然后把am=8，an=16整体代入即可。

例 2.若xn=4，yn=9 则（xy）n=_______

解析：此题是运用积的乘方可以变形为（xy）n=xn·yn，然后把xn=4，yn=9整体代入即可求出结果。

例 3.已知x2y=3，求 2xy（x5y2-3x3y-4x）的值。

分析：此种类型的题目是在单项式乘以多项式之后，再运用积的乘方和幂的乘方逆运用把各个项的底数都化为相同，再进行整体带入。

解：2xy（x5y2-3x3y-4x）=2x6y3-6x4y2-8x2y=2（x2y）3-6（x2y）2-8x2y

当x2y=3时，

例 4.若am=4，an=9 则a3m-2n=_______

解析：此题可以通过同底数幂相除和幂的乘方的逆运用对a3m-2n代数式进行变形为：a3m-2n=a3m÷a2n=（am）3÷（an）2，这时候把am=4，an=9代入即可。

练习：已知ab=3，求（2a3b2-3a2b+4a）·（-2b）的值。

总而言之，利用整体带入求代数式的值就是把已知条件和代数式中的部分项看作一个有机的整体再进行整体带入，从而求出代数式的值。对于已知条件和代数式表面上没有直接关系的，可以利用等式性质对已知条件进行变形或者对代数式进行恒等变形，使其能够整体带入。

练习：

1.已知：2x-2y=14，求 3+x-y的值。

解：因为2x-2y=14

所以x-y=7

所以3+x-y=3+7=10

2.已知 5m+5n-1=4，求（m+n）2+3m+3n的值。

解：因为5m+5n-1=4

所以5m+5n=5

所以m+n=1

3.已知 3a2-a-2=0，求 5+2a-6a2的值。

解：因为3a2-a-2=0

所以3a2-a=2

所以a-3a2=-2

所以2a-6a2=-4

所以 5+2a-6a2=5+（-4）=1

4.已知x-y=3，求x2-y2+2x-8y-4的值。

解：原式=（x-y）（x+y）+2x-8y-4

把x-y=3代入得：

再把x-y=3代入得：

原式=5×3-4=11