造纸废水处理过程中胶体颗粒的聚并机理

Sang Yizhou 刘新亮 蔺爱国

（1.中国石油大学（华东）科学技术研究院，青岛 266580；2.中国石油大学国家大学科技园，东营 257062；3.中国石油大学(华东)化学工程学院，青岛 266555）

在造纸废水处理过程中，絮凝是最主要的方法之一，絮凝效果由絮凝剂决定。传统的无机低分子絮凝剂如铝盐和铁盐，是通过对水中胶体粒子的双电层进行压缩引起絮凝的。由于高分子絮凝剂的高效性，传统的铝盐、铁盐将逐步被有机和无机高分子絮凝剂所替代，高分子絮凝剂通过吸附架桥作用和卷扫(网捕)作用使胶体粒子脱稳发生聚集及沉降。造纸废水处理过程中胶体颗粒的絮聚包括传输和附着两个过程，前者用碰撞频率描述，后者用碰撞效率描述[1]。按照造纸废水中胶体颗粒的大小和密度不同，胶体颗粒的碰撞机制包括由流体分子热运动引起的布朗运动产生的碰撞频率函数[2]，由流体运动（包含层流和湍流运动）导致的碰撞频率函数[2]和由差速沉降作用（颗粒的尺寸和密度不同）产生的碰撞频率函数[3]。Adler[4]首次提出针对层流剪切作用的碰撞效率计算公式。Kusters等[5]基于Adler4碰撞效率计算公式，提出了针对可渗透絮凝体的壳-核模型。Selomulya等[6]提出了一个类似的简化公式并计算了碰撞效率。Antunes等[7]采用该简化公式对沉淀碳酸钙混凝过程进行了模拟。研究结果表明，相对于支链聚丙烯酰胺，直链聚丙烯酰胺引起的水处理过程颗粒絮凝效果更好，能引起更高的碰撞效率；不同的絮凝剂浓度作用下碰撞效率与絮体破碎参数均会发生变化，但并未给出相关规律。Sang等[8]的研究表明，相比于电荷密度低的木薯淀粉，电荷密度高的阳离子淀粉能引起较高的胶体颗粒碰撞效率。Samaras等[9]认为，碰撞效率是絮凝剂吸附量的函数，但是这些研究并未考虑破碎系数的变化。Mietta等[10]认为，碰撞效率与破碎系数的比会随着Zeta电位 （绝对值）的增加而减小。

由于造纸废水处理过程中絮凝现象的普遍性和重要性，混凝动力机制在理论分析方面的研究也取得了重要进展。但是传统Smoluchowski模型假设颗粒是没有空隙的实心球体，碰撞结合在一起后形成的絮凝体仍是密实的球体，这显然与絮凝体是包含颗粒和封闭水在内的多空隙结构的实际情况不符[11]。将絮凝体分形特征引入Smoluchowski模型，能很好地描述不规则絮凝体结构内部的填充程度和絮凝体结构的形成、絮凝体生长和破碎过程等[6，12]。考虑了絮凝体结构在絮凝过程中变化的模型显著改善了对絮凝体粒径的预测[13]。改善后的群体平衡模型（population balance model，PBM）被应用于废水处理系统[14]及混凝体系[6]中，可由式（1）表示。

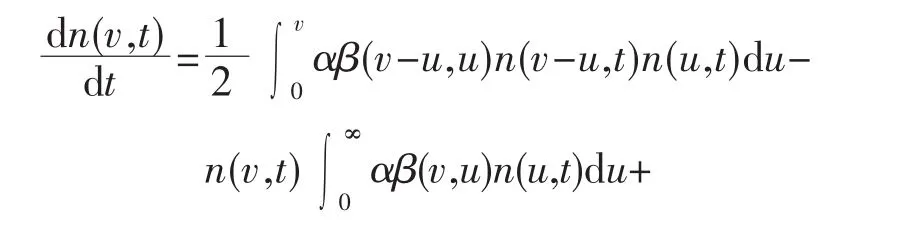
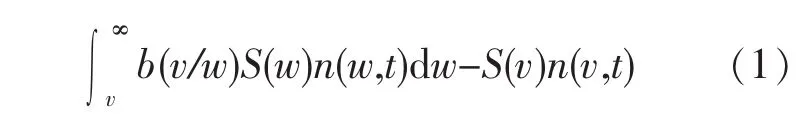
式中：等号右端的第一项和第二项表示聚合过程，前者表示颗粒由体积颗粒和颗粒聚合生成 （系数1/2确保同样的聚合不被重复计入），后者表示颗粒（v）与其他颗粒（u）聚合后的自身消亡；右端第三项和第四项表示破裂过程，前者表示大颗粒（w）破碎为小颗粒（v）的生成项，后者表示颗粒（v）破碎后的自身消亡；α 为聚并效率；β（v-u，u）为颗粒（v-u）和颗粒（u）的碰撞频率；b（v/w）为大颗粒（w）破碎为小颗粒（v）的分布函数；S（w）为颗粒（w）的破碎频率。

在群体平衡模型的框架下，颗粒的絮聚、絮体的破碎及重组模型是核心。在过去的几十年中，废水处理过程中胶体颗粒的聚并和破碎现象已经引起了广泛的理论和实验关注。文献给出了许多描述破碎频率、子颗粒粒径分布函数、碰撞频率和聚并效率的模型。针对造纸废水处理过程的胶体颗粒聚并和破碎频率的模拟非常复杂，并且要基于碰撞频率、破碎频率、子颗粒粒径分布、聚并和破碎概率的知识。由于对这些过程的理解有限，现在仍然采用经验关系式，难以构建理想预测模型对造纸废水处理过程进行有效预测及调控。到目前为止，还没有出现考虑全部机理并适用于广泛条件的令人满意的模型[15]，本文试图综合论述各种机理和根据文献可得的针对废水处理过程中胶体颗粒的聚并模型。

1 胶体颗粒聚并机理

与造纸废水处理中絮聚体的破碎过程相比，胶体颗粒的聚并过程更复杂，因为它不仅包括胶体颗粒与周围液体的相互作用，而且还包括当胶体颗粒受外力或自身力作用聚集到一起时胶体颗粒之间的相互作用。当前，针对胶体颗粒聚并过程提出了三种理论，其中最流行的理论是液膜排液模型。在胶体颗粒碰撞以后，由于两个胶体颗粒间液膜的存在，两个胶体颗粒黏合在一起，但此时并未聚并。两个胶体颗粒间的吸引力促使液膜排出直至破裂，随后发生胶体颗粒聚并。为简单起见，胶体颗粒的聚并过程常常被划分为三个可控的子过程：（1）两个胶体颗粒碰撞并在两个胶体颗粒间锁住少量液体；（2）两个胶体颗粒保持接触直到液膜排液到临界厚度；（3）液膜破碎导致胶体颗粒聚并。实际上，胶体颗粒碰撞持续时间有限，因为只有当液膜的相互作用时间足够并允许其达到临界破碎厚度时胶体颗粒聚并才可能发生。从分子本质上考虑，相比于控制聚并概率的湍流力，胶体颗粒碰撞界面的吸引力太弱[16]。在胶体颗粒强力碰撞过程中，当两个碰撞胶体颗粒的渐近速度超过临界值，不会形成液膜及其后的排液过程，瞬时聚并将是主导机理。低的碰撞速度会导致高的聚并效率，基于此实验结果提出了临界碰撞速度经验模型[17-18]。

在所有情况下，接触和碰撞是聚并的前提。胶体颗粒间的碰撞常常由它们的相对速度引起。多种机理可导致相对运动。在湍流中，至少可以区分五种引起相对运动的来源：（1）周围连续相中的湍流波动；（2）流体中的平均速度梯度；（3）由浮力或体积力导致的不同气泡上升速度；（4）涡流中的气泡捕捉；（5）尾流交互作用或螺旋/之字形流体路径。假定由不同机理引起的碰撞是累积的[19－20]，针对不同来源相对速度引起的碰撞推导出不同的碰撞频率模型。由于不是所有的碰撞都引起聚并，引入了碰撞效率概念。碰撞频率和聚并效率决定了聚并频率。

2 经验模型

广泛应用的模型为含有可调节参数的幂函数形式。通过关联实验数据发展了式（2）表达式[21]。

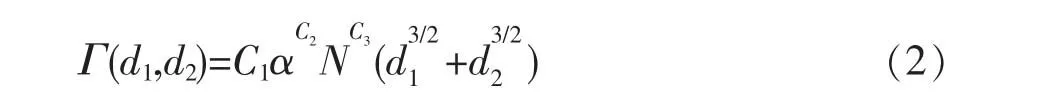
式中：Γ 为聚并频率，m3·s-1；d1，d2为两个碰撞胶体颗粒的直径，m；C1，C2，C3为可调参数；α 为容积比；N 为搅拌速度，s-1。

针对污水处理的搅拌器提出了式（3）所示的模型[22]。

式中：Γ 为聚并频率，m3·s-1；d1，d2为两个碰撞胶体颗粒的直径，m；C5，C6，C7为可调参数；α 为容积比；N 为搅拌速度，s-1。

半经验模型[23]的形式为

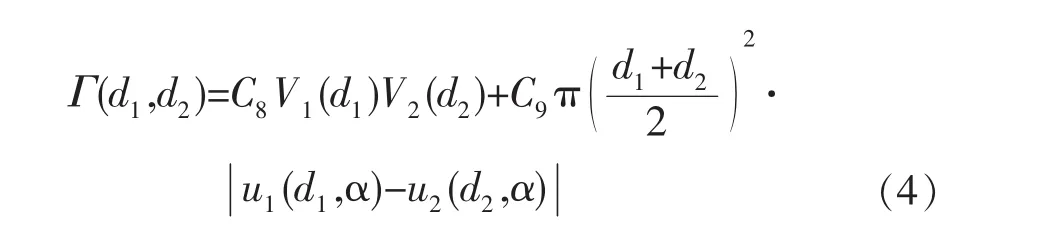
式中：等式右侧第一项是由随机运动引起的聚并频率，假定正比于胶体颗粒体积；第二项代表由不同上升速度引起的聚并；C8，C9为可调参数；V1，V2为胶体颗粒体积，m3；u1，u2为胶体颗粒的速度，m·s-1。

通过比较瞬时分布的模型预测值和实验数值，指数函数能提供相较于幂函数更好的吻合[24]。

式中：C10，C11，C12为可调参数。

但是，这些经验模型的局限性也是显而易见的。比如，它们依赖于实验装置或者装置的几何形状参数，所以结果不能随意应用于其他情况。当使用基于含有多个可调节参数的任意函数形式的经验模型来拟合某一组实验数据，其很难解释潜在的物理定律。

3 物理模型

造纸废水处理过程中的物理模型利用碰撞频率和聚并效率来计算聚并频率，基于定义碰撞机理的物理数值推导物理模型，模型的基本形式如式（7）所示。

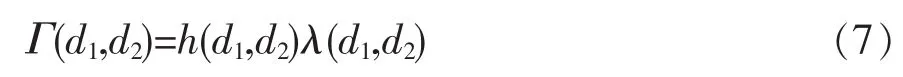
式中：h 为碰撞频率，m3·s-1；λ 为聚并效率。

3.1 碰撞频率h(d1,d2)

多种机理能引起造纸废水处理过程中胶体颗粒之间的碰撞。湍流波动、全局速度梯度、涡流中的气泡捕捉、浮力和尾流作用均能引起的胶体颗粒碰撞。显然，由湍流波动导致的胶体颗粒无规则运动会导致碰撞。另外，高流体速度区的胶体颗粒可能与相对低流体速度区的胶体颗粒碰撞。而且，如果两个胶体颗粒同时被同一个涡捕捉，由于涡的剪切力，这两个胶体颗粒可能聚并。最后，因为体积力和尾流交互作用，不同大小的胶体颗粒有不同的运动速度并且可能互相碰撞。

3.1.1 湍流无规运动引起的造纸废水处理过程胶体颗粒碰撞

湍流速度波动可能会引起造纸废水处理过程中胶体颗粒的碰撞。湍流中胶体颗粒的无规运动常常被假定为与经典气体动理论中气体分子的无规律运动类似，这是一个粗略的假设，因为胶体颗粒既不是刚性，它们之间的碰撞也不是弹性碰撞。Kennard根据气体动理论认为，造纸废水处理过程胶体颗粒碰撞的碰撞频率可表示为单位时间内颗粒运动扫过的有效体积[25]：

式中：urel为碰撞胶体颗粒间的相对速度，m·s-1；S12是胶体颗粒的碰撞截面积，用式（9）计算。

为了确定胶体颗粒间的相对速度urel，通常假定碰撞胶体颗粒与同等大小的涡具有相同的速度[20，26-28]。小的涡流没有足够的能量来影响胶体颗粒的运动，大的涡流仅仅是搬运胶体颗粒，但对相对运动没有影响。所以，大小分别为d1和d2的胶体颗粒的相对速度正比于当量涡速度的均方根：

式中：ut1是大小为d1涡的速度；ut2是大小为d2涡的速度。

应用经典湍流理论，涡速度ut可表示为

式中：ε为湍流涡流耗散率。

碰撞频率[28-29]可表示为

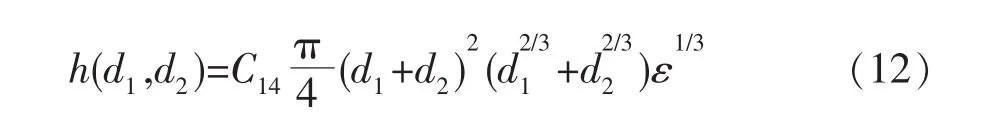
式中：C14为可调参数。

如果胶体颗粒的尺寸大于湍流le的积分尺度，湍流涡在胶体颗粒搬运方面不再高效，胶体颗粒的相对运动主要是因为流体的平均剪切应力。因此，湍流内胶体颗粒碰撞只在以下情况下发生：

式中：Ct系数考虑了胶体颗粒和液体涡之间的速度差异；因数考虑了由于虚质量的增大导致的靠近胶体颗粒减速。

考虑胶体颗粒的存在降低胶体颗粒移动的自由空间并导致碰撞频率的提高，此效应可用碰撞频率与系数γ相乘表示。另一个修正是胶体颗粒间平均距离和他们平均相对湍流路径长度之间的比例。当胶体颗粒间的距离大于湍流路径长度时，没有碰撞发生，所以应该引入因数Π[30-31]：

式中：lt是促使大小分别为d1和d2的胶体颗粒碰撞的涡平均大小；hb，12是大小分别为d1和d2的胶体颗粒间平均距离；C16为可调参数。

通过假定涡的平均大小与气泡的大小在同一个数量级上，因数的最后形式为

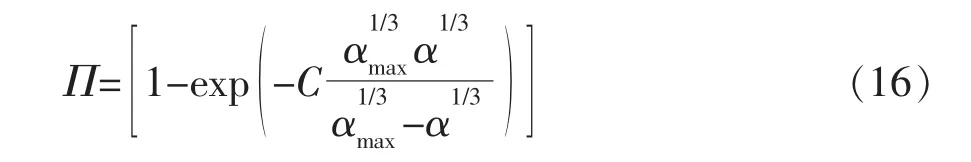
式中：α，αmax为体积分数；C是依赖于流体特征的可调参数，的值小时，Π 接近的值大时，Π趋向零。这一规律可用公式[31-32]表达为

本质上，C17为可调参数；参数Π和γ扮演了相同的角色，它们都与体积分数α或者胶体颗粒数量密度相关。小的胶体颗粒具有小的碰撞频率，这是因为在胶体颗粒数量一样的情况下，小胶体颗粒间的平均距离比大胶体颗粒间的平均距离要大[31-32]。如果平均距离大于湍流平均路径长度，胶体颗粒碰撞频率将成指数降低。

3.1.2 速度梯度引起的造纸废水处理过程胶体颗粒碰撞

通常在未加验证的情况下，全局速度梯度、涡的胶体颗粒捕捉、浮力和尾流作用被忽略。因为速度梯度，均匀层流中的胶体颗粒可能会互相碰撞，这种速度梯度在湍流中同样占主导地位。假定流线是直的并且颗粒的运动也是直线，均匀层流中剪应力引起的碰撞频率函数为[33]

式中：lb，12是大小分别为d1和d2的胶体颗粒的平均相对湍流路径长度尺度。

最后，修正后的碰撞频率可表示为

式中：r1，r2为胶体颗粒半径，m；ShR为剪切速率，s-1。理论上，上述模型适用于任何由速度梯度引起的胶体颗粒碰撞[33]。

3.1.3 涡的胶体颗粒捕捉引起的造纸废水处理过程胶体颗粒碰撞

当湍流中胶体颗粒尺寸小于能量耗散涡尺寸时，主导碰撞的力为黏性力[34]。换言之，胶体颗粒速度将与连续相流场的速度非常接近。这与密度差异被忽略的情况类似。在这种情况下，碰撞频率仅仅被湍流涡的局部剪切决定，它可以用与均匀层流剪切流类似的方式表示为

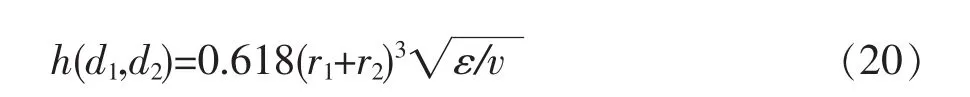
3.1.4 浮力引起的造纸废水处理过程胶体颗粒碰撞胶体颗粒碰撞可能是由于不同尺寸胶体颗粒的

运动速度不同引起的[20]。浮力引起的胶体颗粒碰撞频率计算模型为[33]

式中：S12是碰撞胶体颗粒的碰撞截面积；ur1，ur2为胶体颗粒运动终速度，m·s-1，由体积力（浮力）导致的上升速度来计算相对速度。

3.1.5 尾流夹带引起的造纸废水处理过程胶体颗粒碰撞

当胶体颗粒在液体中自由运动时，一部分液体不可避免地被夹带并被加速，我们称之为尾流[35]。尾流引起的碰撞主要导致流体中具有足够黏性并使尾流保持平流的胶体颗粒之间的聚并[36]。应用描述尾流速度分布的关系式[37]，推导出碰撞频率为

式中：C18的单位是 s-1·m-2，此参数由实验确定。

考虑尾流相互作用、胶体颗粒速度和胶体颗粒形状，发展了胶体颗粒-胶体颗粒相互作用的模型[38]：

式中：urel是两个碰撞胶体颗粒之间的相对速度；(lw)是系统中胶体颗粒间的平均距离是受大小为d1的胶体颗粒尾流影响的体积，被假定为圆锥形[39]。圆锥形的底座是先行胶体颗粒的截面积，在实验结果的基础上，假定高度5倍于底座直径。假定胶体颗粒大小分布均匀，提出了由于尾流夹带造成的胶体颗粒聚并模型[30]：

式中：C19是依赖于尾流区的形状和大小的可调参数。

因为尾流区胶体颗粒的相对速度不仅依赖于胶体颗粒与连续相之间的相对速度urel、尾流形状，而且还依赖于曳力系数CD，Hibiki等通过加入项进一步提炼了模型[40]，改进后的模型为

式中：C20是依赖于尾流形状和胶体颗粒形态的可调节参数；CD为界面曳力系数；d1是胶体颗粒的直径。

总之，湍流中的胶体颗粒碰撞可由多种机理引起。尚没有模型考虑了全部的机理。同时，很难确定哪种机理在特定状况下发挥了最重要的作用。一般而言，如果在湍流惯性子区的尺寸范围内，胶体颗粒将受到来自各个方向的涡压力，此时，无规则运动将是最重要的。如果胶体颗粒小于Kolmogorov消散尺度，滑移速度可以忽略，相对速度主要由局部的湍流特征来决定（比如湍流剪切力），层流剪切力（比如平均速度梯度）影响了各个尺寸气泡的相对运动。而且，随着密度差异增大，浮力机理变得更重要。

3.2 聚并效率

大多数碰撞的胶体颗粒在碰撞后会分开，仅仅一部分碰撞能导致聚并。所以，引入效率概念来描述聚并过程。能量模型、临界速度模型和液膜破碎模型是3种有代表性的聚并效率模型。

3.2.1 聚并过程的能量模型

相当大一部分胶体颗粒的碰撞导致了即时聚并，随着碰撞能量的提高，聚并的概率率随之提高[41－42]。高能碰撞模型将胶体颗粒的动力碰撞能量()与界面能关联起来，见式(16)。

式中：C21是可调节参数。

胶体颗粒的界面能正比于界面张力和表面积，即

动力碰撞能量Ekin被假定正比于平均体积和两个碰撞胶体颗粒的相对速度urel，计算式为

式中：ρd为连续相密度，kg·m-3。

聚并效率可写为

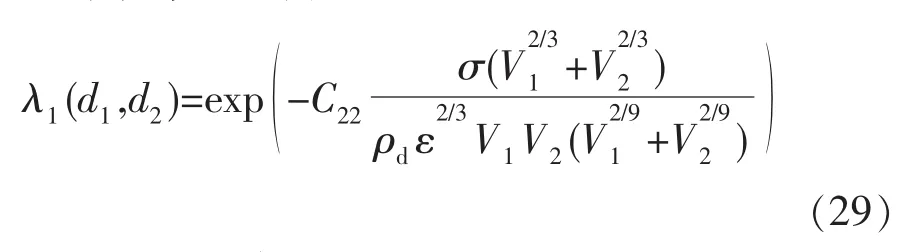
式中：C22是调节参数；σ 为表面张力，N·m-1；ε 为湍流涡耗散率。

根据造纸废水处理过程胶体颗粒碰撞过程的动量平衡计算出动力碰撞能量为[43]

并推定效率为

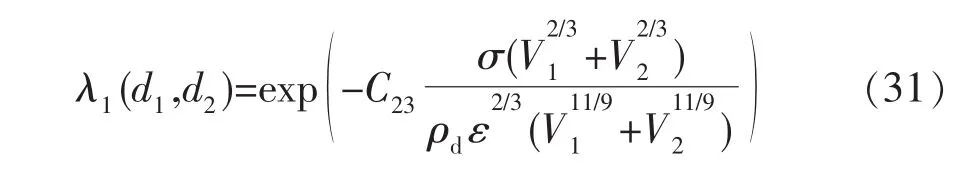
式中：C23是调节参数。

最后，将能量模型与液膜破碎模型结合，得到的总碰撞效率为[44-45]

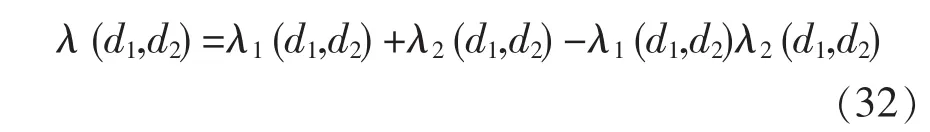
式中：λ2(d1，d2)从胶体颗粒液膜破碎模型得到。

3.2.2 造纸废水处理过程中胶体颗粒临界速度模型

根据能量模型，在碰撞瞬间，当碰撞速度超过临界值时，聚并会立即发生。另一方面，温和的碰撞更有利于聚并[46-47]。式（33）的表达式关联了聚并效率和碰撞速度[18，48]。

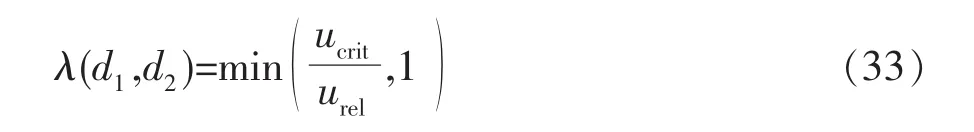
3.2.3 造纸废水处理过程中胶体颗粒液膜破碎模型

造纸废水处理过程中胶体颗粒液膜破碎模型从胶体颗粒的接触时间和液膜的破碎时间两个特征时间尺度来确定碰撞效率，这两个时间决定了胶体颗粒能否发生聚并。其中，液膜的破碎时间是胶体颗粒间的液膜变薄至临界厚度所需的时间。假定聚并和接触时间是随机变量，利用正态分布的概率密度函数计算聚并效率[49]，计算公式为

式中：σtdrainage为变量tdrainage的分布偏差；tdrainage为液膜排液时间，s；tcontact为气泡接触时间，s；erfc()为互补误差函数。假定聚并时间不分散，即σtdrainage=0，式（34）被简化为[50]

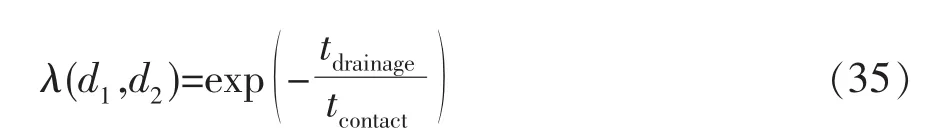
尽管在文献中存在针对两个时间尺度、随机变量和正态分布假设有效性的批评[51]，但是液膜破碎模型仍是迄今为止最流行的并且几乎是其后全部模型的出发点。不同模型之间主要的区别在于对接触时间tcontact和液膜破碎时间tdrainage的表达。

（1）液膜破碎时间

根据胶体颗粒表面刚度（可形变和不可形变）和接触表面的可滑移性（非滑移、部分滑移、滑移），分辨出不同的液膜破碎状态。大部分对液膜破碎状态的分析采用润滑理论，从纳维-斯托克斯方程和连续性方程开始，推导出变薄方程。对简单的边界条件，如恒定的相互作用力或恒定的碰撞速度，液膜破碎时间可以通过对液膜变薄方程进行积分获得。

(a)不形变胶体颗粒的聚并

当造纸废水处理过程中的胶体颗粒与连续相相比非常黏或者非常小(d＜1 mm)，在远距离时，他们的界面会略微变形并且表现为接近刚性球体颗粒。对于两个同等大小的不可形变球体，利用泊肃叶定律推导出胶体颗粒破碎时间为

式中：μc为动力黏度，Pa·s；F 为压缩力，N；hi，hf为初始和临界液膜厚度，m。如果用等同半径req=2r1r2/(r1+r2)来替代胶体颗粒半径r，式(36)可用于描述不同大小胶体颗粒[52]，变形为如下形式[53-54]：

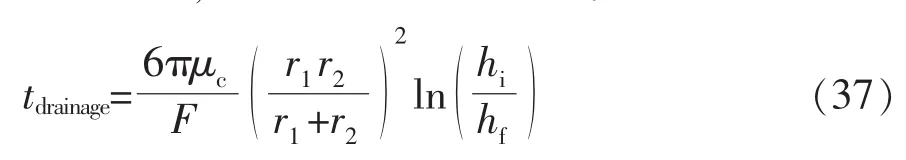
但是，假定造纸废水处理过程中胶体颗粒不发生形变只对非常小的胶体颗粒合理（db＜1 mm）。在大多数应用中，由于大胶体颗粒的存在，碰撞过程中胶体颗粒表面的形变必须考虑[43]。

最简单的可形变界面液膜破碎模型被称为平面膜模型，其假定聚并胶体颗粒的表面形变为两个半径为Ra的平面膜。但是，实验中发现液膜为曲面膜，这表明形变界面存在压力梯度[55]。

（b）液膜不可移动的可形变颗粒

对可形变颗粒液膜排液状态的划分依赖于液膜的可移动性。对于不可滑移液膜，液膜排液由黏性变薄控制。液膜受两个刚性表面之间的平流影响而被挤压出。液膜中的速度分布是抛物线，并且在界面没有滑移。Chesters推导出了针对恒定压力情况下的排液时间[34]，见式(38)。

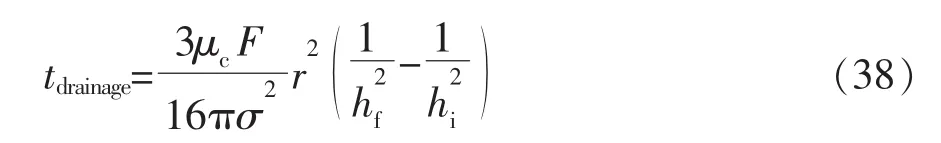
对两个不同大小颗粒的情况，如果气泡的半径r用等效半径req替代，则有

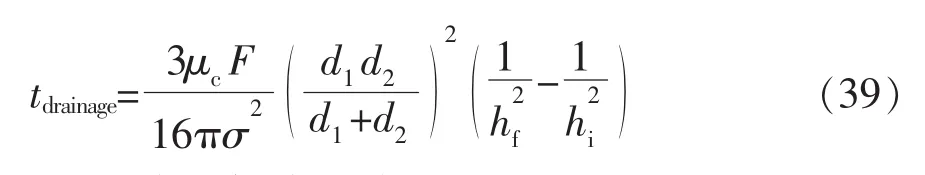
（c）液膜可部分滑移的可形变颗粒

对不滑移液膜界面的近似只适用于超高分散相黏度或者含有一定浓度表面活性剂的系统。液膜排液主要由液膜的移动来控制。假定其是准稳定的蠕动流，Chesters利用式(40)计算了部分滑移界面的排液时间[34]。

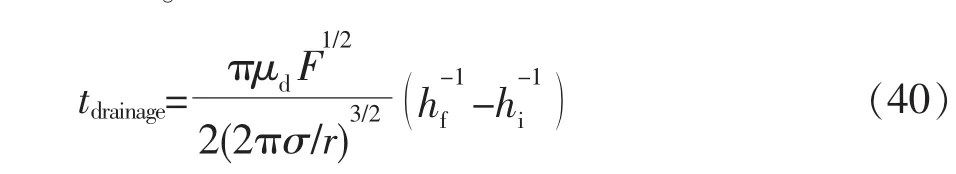
Lee等将Sagert等[56]的模型用于部分滑移界面得到

（d）可形变颗粒的滑移界面

对滑移界面采用平面膜模型，Chesters[34]提出了式(43)所示的排液方程。

由惯性力控制的另外一种极限情况是湍流中胶体颗粒的情况，式（44）被简化为

式中：ρc为分散相密度，kg·m-3；ut为涡速度，m·s-1。

上述模型被Luo[28]发展为针对大小分别为d1、d2的胶体颗粒模型，得到

从式(46)可以看出，惯性变薄的排液时间正比于胶体颗粒靠近速度u12。这意味着当靠近速度u12很低时，排液时间很短，此时聚并效率很高，这与临界速度模型的观点一致。Lee等[29]的研究表明，惯性变薄对非黏性流体(μc＜10 mPa·s)起主导作用：

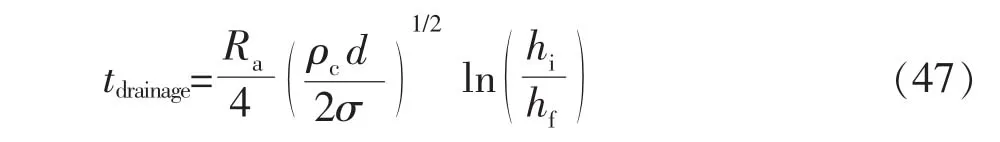
忽略Hamaker力，模型可简化为

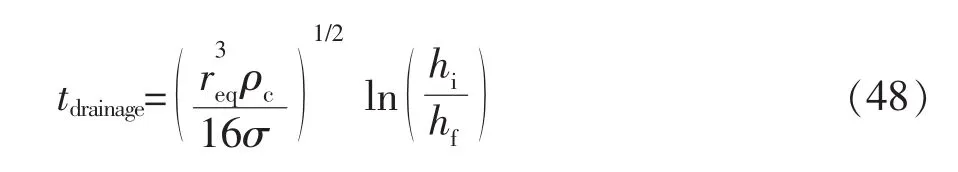
（2）压缩力

为了使用上述表达式来描述聚并过程中的液膜排液过程，需要用到碰撞过程中的相互作用力F。F通常不是常数。流体胶体颗粒和连续相之间的曳力、靠近过程中的接触面积和胶体颗粒本身的振荡均会引起相互作用力的波动。假定相互作用力F正比于大小为当量直径的涡任何一端速度差的方差[26，57-58]，即

式中： ρc为分散相密度，kg·m-3；ε 为湍流涡耗散率。

废水处理过程湍流中黏性碰撞和惯性碰撞的碰撞力和碰撞时间由Chesters给出。对应于远小于Kolmogorov尺度胶体颗粒的黏性状态，两个相撞胶体颗粒之间的典型力正比于湍流剪切力如式（50）所示。

另一方面，对于惯性碰撞，Chesters指出：因为惯性，一个颗粒作用与另一个颗粒上的作用力F大于由式（50）计算得到的数值，因为式（50）计算得到的数值是由表面流施加的力。此时的关系式为

（3）接触时间

对湍流系统中相互作用时间的计算，先前的大部分研究使用基于因次分析得到的关系式[59]

Chesters[34]指出，碰撞力和时间是由表面流控制的，将其与黏性简单剪切中的固体颗粒类比，总结出湍流中黏性碰撞时的颗粒接触时间反比于最小涡流中流体的应变率，即

在惯性碰撞中，存在从动能到表面能转化的过程。从这点来看，惯性系统的实际接触时间小于由式(53)得到的结果[34]。考虑虚质量，从能量守恒推导出接触时间为

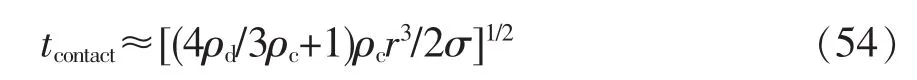
基于简单的平面膜模型，推导出更合理的接触时间表达式为[28]

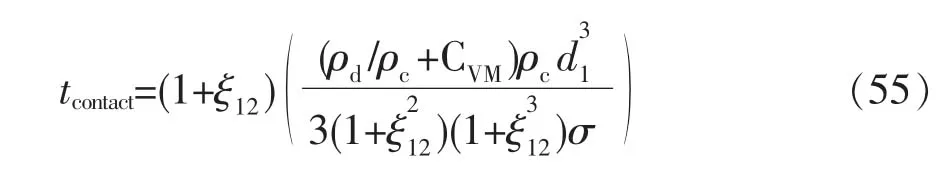
式中：CVM是附加质量系数，尽管在胶体颗粒靠近过程中它是可变的[60]，但通常被认为是介于0.5～0.8的常量[61]；ξ12为 r1/r2。

胶体颗粒的相互作用时间是从液膜形成开始到胶体颗粒开始弹回为止。假定表面自由能增加与对应的系统动能减少之间存在一个平衡，得到相互作用时间为[60]

大多数模型仅仅考虑了由湍流波动引起的惯性碰撞并是根据各向同性湍流经典理论推导得出的。将湍流中的碰撞划分为黏性碰撞和惯性碰撞[34]。同时，除湍流之外也考虑了浮力、剪切力和尾流相互作用[20，31-32，62]阐明不同碰撞的聚并效率模型可能有不同的形式[63，31-32]。通过改进接触时间，从而考虑不同碰撞源对聚并效率的影响[62]。所有的聚并效率公式给出的都是介于0～1的数值。由各个模型算出的数值可能存在差异，但是，多数模型都表现出对胶体颗粒尺寸的依赖，即随着胶体颗粒尺寸增大，聚并效率降低。

4 讨论和展望

在开发复杂模型的过程中，描述湍流效应、界面传递、胶体颗粒聚并和破碎过程的封闭关系是不可或缺的。对胶体颗粒聚并和破碎的模拟研究比较薄弱[64-65]，胶体颗粒的相对运动导致了胶体颗粒间的碰撞，聚并可能在其后发生。对于湍流，至少五种机理与胶体颗粒的相对速度及其随后发生的碰撞有关，即湍流波动、平流剪切力、湍动涡捕捉、由体积力引起的不同上升速度及尾流夹带。但是，到目前为止，由不同机理引起的碰撞频率计算和它们作用的累积结果都是基于任意假定和经验关系，如气体动理论、各向同性湍流及锥形形状尾流。

此外，在多分散流中通常要考虑胶体颗粒大小分布的空间依赖性；如果不考虑此问题，基于实验数据就可得到可调模型参数。聚并闭合的输入参数也没有完善的定义，尤其是湍流参数。由胶体颗粒引起的湍流调制也没有得到很好的理解。许多CFD（Computational Fluid Dynamics）代码通过修正湍流黏度来考虑胶体颗粒引起的湍流，采用这种方法有可能得到令人满意的流速场模拟，但是较依赖于实施。湍流参数，如湍流动能的耗散率，是碰撞模型中的重要输入参数。

许多研究关注由湍流运动引起的碰撞。非稀释流常常是聚并模拟的焦点，在模拟过程中必须考虑胶体颗粒自由运动空间的减少。另一方面，气泡间自由距离、涡流与胶体颗粒之间速度差、虚质量的影响还需要进一步研究。

对聚并模型的改进，应从以下几个方面考虑：

（1）模型应该基于物理观察、胶体颗粒大小、流体特性和湍流参数。

（2）模型应包括所有的潜在机理；但是对特定情况，有些机理可以忽略。

（3）有必要认真检查碰撞频率前因子的重要性；有些前因子考虑了由于胶体颗粒存在导致胶体颗粒运动自由空间减少，有些因子仅仅是对湍流碰撞不可缺少。

（4）每种机理引起的碰撞效率都是不同的。

（5）应该考虑胶体颗粒引起的湍流，聚并闭合须嵌进模型并为液相提供湍流参数。

（6）应该考虑空间效应，使可调参数适应更广的流体状况。