基于有限元分析的转辊式无针头静电纺电场优化

刘延波 ，杨媛媛 ，陈 莉 ，刘 健 ，杨文秀

（1.天津工业大学 纺织科学与工程学院，天津 300387；2.武汉纺织大学 纺织科学与工程学院，武汉 430200；3.天津工业大学 天津市现代机电装备技术重点实验室，天津 300387）

自1934年Formals[1-2]公开发明了一种利用静电斥力来生产聚合物纤维的装置，并申请了专利以后，静电纺丝技术已成为一种切实可行的获得微纳米纤维的方法.目前国内外纳米纤维规模化制备技术基本上分为多针头静电纺丝技术[3-4]和无针头静电纺丝技术[5-8]两大类.相对于单针头静电纺丝技术而言，多针头静电纺丝技术生产效率大大提升，但是存在难以克服的边缘效应现象[9-10]，且针头易堵，难以清洗，使得多针头静电纺丝技术多年来难以有质的飞跃.无针头静电纺丝技术则从根本上避免了针头易堵的问题[11]，但仍存在一定程度的边缘效应现象，所得纳米纤维离散较大，且纺丝质量均匀性、前后一致性难以保障[12].为解决上述问题，本文通过对纺丝头进行倒角处理和增加辅助电极的方法改善转辊式无针纺丝头的场强均匀性，并采用COMSOL Multiphysics有限元模拟软件对倒角处理前后和增加辅助电极前后的转辊式无针头静电纺丝过程中的电场强度和分布进行模拟研究.

1 COMSOL静电场模拟原理与建模

1.1 COMSOL静电场模拟原理

COMSOL Multiphysics是以有限元法为基础，通过求解偏微分方程单场或偏微分方程多场来实现物理现象的仿真，目前已经在声学、生物科学、化学反应、弥散、电磁学、流体力学、量子力学等等领域得到广泛应用.COMSOL Multiphysics有限元模拟过程包括：确定模拟项目→建立模型→设定求解与边界条件→划分网格→求解→后处理[13].该软件包括一个基本模块和8个专业模块，专业模块分别为AC/DC模块、声学模块、化学工程模块、地球科学模块、传热模块、MEMS模块、RF模块以及结构力学模块，可以任意组合不同模块中的应用模式实现多物理场的耦合模拟.本文使用COMSOL Multiphysics有限元模拟软件中AC/DC模块下的静电模块[14]对静电场进行模拟，且静电场遵循泊松方程：

式中：ε0为真空介电常数；εr为介质的相对介电常数；V为电势能；ρ为空间电荷密度.此方程中各个变量对应的数值在求解域选项中进行设定.本文模拟中，ρ为0 C/m3，接收板和纺丝电极均为金属材质（钢），相对介电常数εr为1.5.

1.2 COMSOL建模

图1为具体的静电纺丝实验模型图，其主要参数和规格如表1所示.

图1 静电纺丝模拟模型Fig.1 Simulation model of electrospinning process

表1 静电纺丝模型基本参数Tab.1 Basic parameters in electrospinning model

2 转辊式无针头静电纺电场优化

纺丝头中间部分由于受到两侧强度相同的电场干扰，叠加后的横向库仑斥力接近于0，因此中间场强被削弱；而纺丝头的两端分别只受到来自一侧的横向叠加库仑斥力的作用，所以纺丝头两端场强大于中间场强.因此，转辊式纺丝电极的场强分布也呈现中间小、两端大的规律，也存在边缘效应，和多针头静电纺丝过程出现的场强分布不均匀现象一致.本课题组以前对多针头静电纺丝过程中出现的边缘效应现象进行过深入系统的研究，并提出了多种减小边缘效应、改善场强和分布的有效措施[15-20].本文拟通过倒角处理和增加辅助电极的方法减弱转辊式无针头静电纺丝过程中的边缘效应，达到场强均匀的目的.

2.1 倒角半径对纺丝头场强分布的影响

采用UG8.0对不同倒角半径的转辊式无针头静电纺丝头进行建模，模型如图2所示，其电场强度分布如图3所示.

图2 不同倒角半径的转辊式无针头纺丝电极模型Fig.2 Rolling needleless spinning electrode model with different chamfering radius

图3 不同倒角半径转辊式无针纺丝头的电场强度分布Fig.3 Electric field intensity distribution of rolling needleless spinneret with different chamfering radius

由图3可以看出：当纺丝头没有进行倒角处理时，两端电场强度远高于纺丝头内部场强，且远高于进行倒角处理的纺丝头两端的电场强度；当进行倒角处理时，倒角半径增加到20 mm时，纺丝头两端的场强值依次降低，整个纺丝头的场强分布呈现从两端向中间依次降低的趋势；当倒角半径继续增加，纺丝头两端的场强仍然呈现依次降低的趋势，但场强分布呈现从两端到中间先增加后降低的趋势.这是由于随着倒角半径的增加，倒角面与纺丝头圆柱面相切，相切处虽然是无缝衔接，但是相对于其他各处来讲，仍然呈现尖端状态，因此，相切处场强增加.不同倒角半径纺丝头的场强平均值和CV值如表2所示.

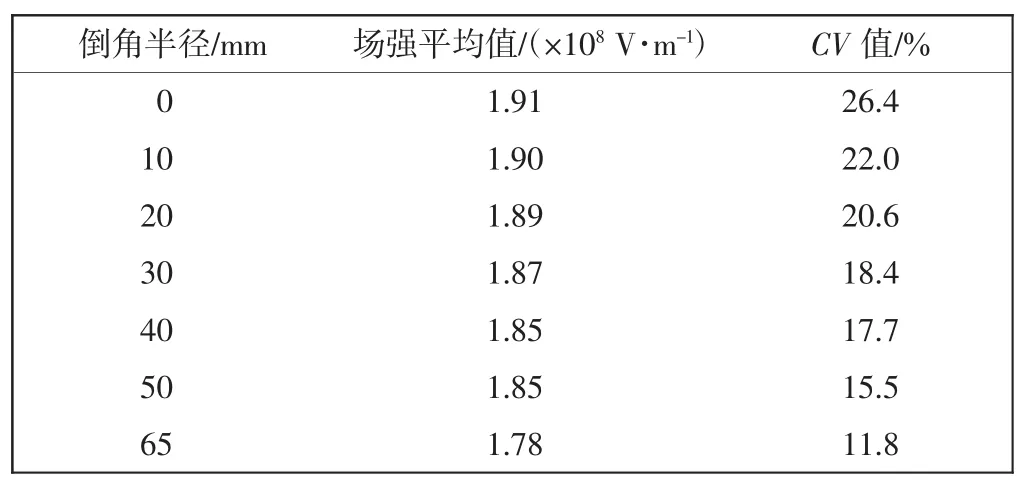
表2 不同倒角半径转辊式无针纺丝头的电场平均值和CV值Tab.2 Average electric field intensity and CV value of rolling needleless spinneret with different chamfering radius

由表2可以看出，随着倒角半径的增加，场强平均值逐渐降低，场强CV值逐渐降低，场强均匀性明显增加.这是由于尖端的相对削弱使电荷分布更加均匀，不存在场强极高的地方，因此场强的平均值也随着电荷的均匀分布逐渐降低，均匀性随之提高.场强CV值从没有进行倒角处理的26.3%到倒角半径为65 mm的11.8%，虽然场强均匀性有明显的提升，但是场强分布变异系数仍然很高.这些变化同样可从图4电场云图的场强颜色变化观察得知，当倒角半径为65 mm时，场强分布较为均匀.

图4 不同倒角半径转辊式无针纺丝头的电场云图Fig.4 Electric field contour graphs of rolling needleless spinneret with different chamfering radius

2.2 辅助电极对纺丝头场强分布的影响

2.2.1 辅助电极直径对纺丝头场强分布的影响

选择辅助电极与纺丝头之间间距45 mm，厚度3 mm，直径分别为 70、100、130、160、190、220 mm 的辅助电极来控制场强均匀性，采用不同直径的辅助电极时纺丝头模型如图5所示.

图5 带有不同直径辅助电极的纺丝头模型Fig.5 Spinneret model with auxiliary electrodes of different diameters

通过COMSOL软件对不同纺丝体系进行电场强度模拟分析，并进行场强大小和均匀性比较.电场强度分布如图6所示.

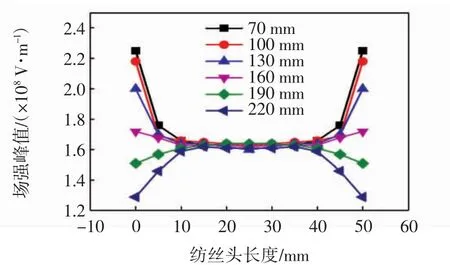
图6 辅助电极不同直径时纺丝头的电场强度分布Fig.6 Electric field intensity distribution of spinneret with auxiliary electrodes of different diameters

由图6可看出，随着辅助电极直径的增加，纺丝头两端的场强值逐渐降低.辅助电极直径增加到160 mm，纺丝头两端的场强值降低到与纺丝头内部场强基本一致.当辅助电极直径继续增加，纺丝头两端场强值低于内部场强值，这是由于随着辅助电极直径的增加，辅助电极位置逐渐高于纺丝头，和纺丝头两端场强产生了排斥.采用不同直径辅助电极时纺丝头的电场平均值和CV值如表3所示.

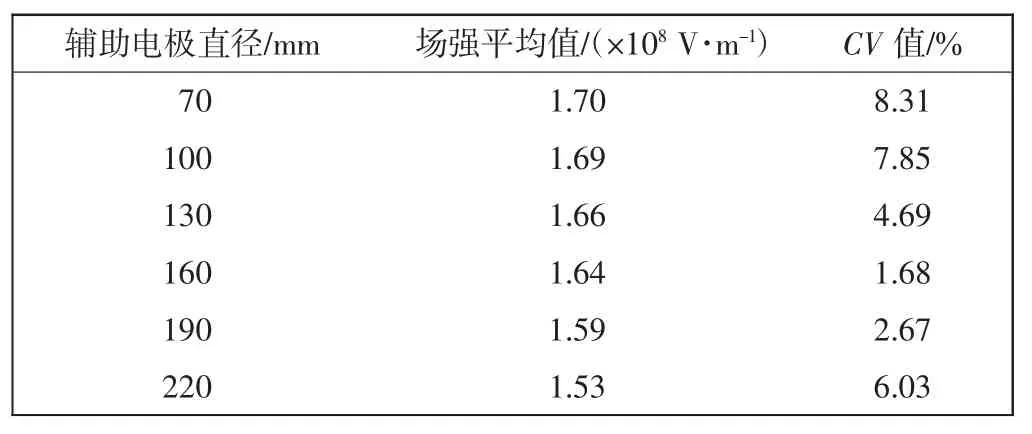
表3 辅助电极不同直径时纺丝头的电场平均值和CV值Tab.3 Average electric field intensity and CV value of spinneret with auxiliary electrodes of different diameters

由表3可以看出，随着辅助电极直径的增加，场强平均值逐渐降低，场强均匀性先降低后升高，当辅助电极为160 mm时，场强均匀性最大，CV值达到最小为1.68%.图7所示为采用不同直径辅助电极时纺丝头的场强分布云图，由图7可见，随着辅助电极的增加，红色部分逐渐依次出现在辅助电极上.这是因为相对转辊来讲，辅助电极的尖端效应更明显，电荷集中在了辅助电极上，在辅助电极产生电场的叠加作用下，转辊两端的场强得到了分散和抵消.因此，辅助电极直径为160 mm时，场强较大且分布均匀，为最佳选择.

图7 辅助电极不同直径时纺丝头的场强分布云图Fig.7 Electric field contour graphs of spinneret with auxiliary electrodes of different diameters

2.2.2 辅助电极距离对纺丝头电场强度分布的影响

图8 辅助电极和纺丝头不同间距时纺丝头的场强分布Fig.8 Electric field intensity distribution of spinneret with different distances between spinneret and auxiliary electrodes

选择辅助电极直径为160 mm，厚度为3 mm，辅助电极和纺丝头之间的距离为 5、15、25、35、45、55 和65 mm进行建模.采用COMSOL有限元分析软件得到不同间距时纺丝头的场强大小和均匀性.图8所示为纺丝头与辅助电极不同间距时纺丝头的电场强度分布.由图8可以看出，随着纺丝头和辅助电极间距的增加，纺丝头两端场强值逐渐增加，当间距小于等于35 mm时，纺丝头两端的场强值小于纺丝头内部场强，这是由于辅助电极高于纺丝头，辅助电极所产生的电场有效抑制了纺丝头两端电场.当间距为45 mm时纺丝头两端电场强度与内部基本保持一致.间距继续增加，纺丝头两端的场强值都略高于纺丝头内部的场强值，这是由于随着辅助电极与纺丝头间距的增加，抑制效果逐渐减弱.表4为不同间距时纺丝头的电场强度平均值和CV值.由表4可知，场强均匀性逐渐提高，场强平均值略有增大，这是由于辅助电极电场对纺丝头电场产生的抑制作用逐渐降低，且抑制作用主要体现在纺丝头两端，对内部影响并不大.这一点也可从图9场强云图中看出.因此，辅助电极和纺丝头间距为45 mm时，场强较大且分布均匀，为最佳选择.

表4 辅助电极和纺丝头不同间距时纺丝头的场强平均值和CV值Tab.4 Average electric field intensity and CV value of spinneret with different distances between spinneret and auxiliary electrodes

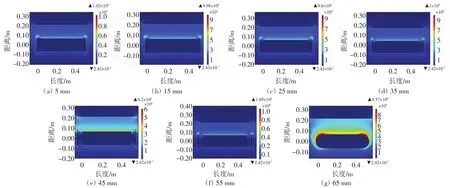
图9 辅助电极和纺丝头不同间距时纺丝头的场强分布云图Fig.9 Electric field contour graphs of spinneret with different distances between spinneret and auxiliary electrodes

2.2.3 辅助电极厚度对纺丝头电场强度分布的影响

选择辅助电极直径为160 mm，辅助电极和纺丝头之间的距离为45mm，辅助电极厚度分别为1、3、5、7mm进行建模，采用COMSOL进行场强模拟分析.辅助电极不同厚度时纺丝头场强平均值和CV值如表5所示.

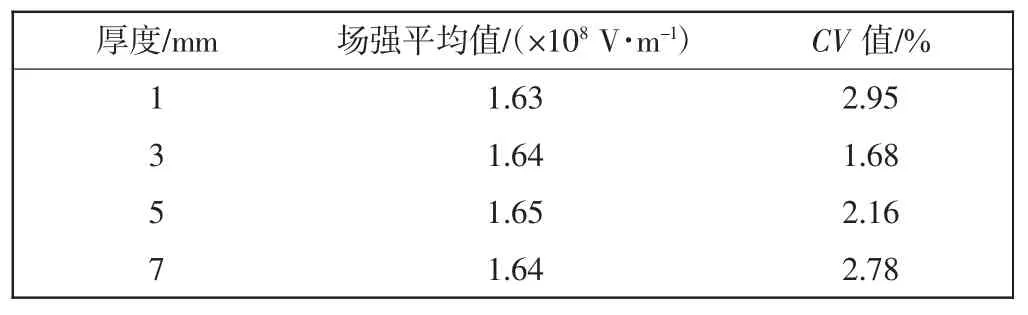
表5 辅助电极厚度不同时纺丝头的场强平均值和CV值Tab.5 Average electric field intensity and CV value of spinneret with auxiliary electrodes of different thickness

由表5可看出，场强平均值基本不变，场强均匀性先升高然后降低，辅助电极厚度为3 mm时场强均匀性最高，但总体来讲场强均匀性变化不大.由此说明，辅助电极厚度对纺丝电极场强大小及均匀性影响不大.考虑到加工过程，选择辅助电极厚度为3 mm.

3 结论

针对转辊式无针头静电纺丝头场强沿轴线分布不匀的问题，通过倒角处理和增加辅助电极两种方式对转辊式无针头静电纺丝头进行改进，并利用COMSOL软件对不同参数调整后的纺丝体系进行静电场模拟，以纺丝头场强平均值及CV值做为评价指标进行对比，发现：

（1）倒角处理对减弱边缘效应有明显效果，使场强CV值从26.3%降低到11.8%.场强平均值随倒角半径增大逐渐降低.

（2）纺丝头尖端的场强平均值随着辅助电极直径增加而逐渐降低，随着辅助电极与纺丝头间距增加而略有增大，随辅助电极厚度增加无明显变化.3个因素对场强均匀性的影响顺序分别为距离＞直径＞厚度.最终选择辅助电极直径为160 mm，厚度3 mm，与纺丝头间距为45 mm.此时场强平均值为1.64×108V/m，场强CV值为1.68%.

（3）与对转辊式纺丝头进行倒角处理相比，增加辅助电极对克服边缘效应和提高场强均匀性具有明显优势，可在不降低电场强度的情况下大大削弱“边缘效应”，提高场强均匀性，改善电纺膜产品质量.