混凝土水化化学反应动力学模型的推导及应用

冯楚桥，余晓敏，常晓林，罗代明，熊 杰

(1. 贵州省喀斯特地区水资源开发利用工程技术研究中心，贵州 贵阳 550002；2. 武汉大学 水资源与水电工程科学国家重点试验室，湖北 武汉 430072)

0 引 言

从结构安全的角度出发，混凝土开裂问题一直是混凝土材料和结构研究的主要关注点。大量的研究成果和工程实践经验表明，混凝土的温度效应和收缩效应与开裂行为紧密相关，尤其在早龄期[1]。温度梯度是大体积混凝土结构产生温度变形的直接因素，在内部及外部的约束作用下，混凝土不能自由变形，最终可能导致温度裂缝的产生。因此，准确地计算并预报混凝土结构内部温度分布及变化特征是控制混凝土开裂的重要措施之一[2]。早龄期混凝土水化过程中胶凝材料与水发生物理化学反应，释放大量的热量并生成复杂的水化反应产物，从而使混凝土的性能发生改变。为了找出一种通用的模型用以描述硬化过程中混凝土的水化热以及物理性质的变化，国内外学者们纷纷开展了大量的研究工作。混凝土水化热归根结底是化学反应中发生的能量变化；强度的增长根本上是化学反应过程中反应物聚合的过程。因此，准确地预报混凝土的水化热及其强度必须从混凝土内部的化学反应开始。

目前，基于化学反应动力学基础的阿伦尼乌斯定律的水化度模型目前已广为接受。采用多孔介质理论和热力学方程，Ulm和Coussy探讨了多孔介质的反应理论，并提出了一种考虑早龄期混凝土化学-热-力耦合因素的模型[3]。Cervera和Oliver等[4]提出了一种水化度模型以模拟混凝土的化学-热-力耦合行为，该模型可在有限单元法中实现并可预测水化度和水化热随时间的演化规律，结合一系列的等温和绝热混凝土试件的水化试验，模型预测值基本与试验值吻合。Maekawa和Ishida等[5]建立了DuCom微观粒子水化模型，该模型可用于水分及热量在混凝土中的传导过程。Lackner和Mang等人找到了用于描述本构方程的材料断裂能与水化度之间的关系，提出了另一种多项式描述水化反应化学亲和力的公式[6]。Gawin和Pesavento等基于前人的研究作出改进，提出了一种水化模型，该模型不仅考虑混凝土的温度场和化学场，而且可以考虑耦合的水分扩散过程[7]。Smilauer和Krejci[8]等借助开源软件CEMHYD3D(美国国家标准和技术研究院NIST开发，Dale P. Bentz[9]进行了一系列改进)，采用的微观模型研究了混凝土结构的宏观热传导问题。Di Luzio和Cusatis等[10]也提出了一种水化度模型，补充研究了高性能混凝土中的温度变化、水分传输以及损伤开裂等行为。

一般而言，在描述混凝土化学-热-力耦合过程中，可通过引入反应系统内部变量水化度以及其他相关联的参数进行计算机数值模拟。这些数值计算方法和手段为评估早龄期混凝土的热、力学性能演变过程提供了有效途径。国内对于混凝土水化特性的研究比较少，目前大体积混凝土温控防裂设计中，通常在有限元法中应用绝热温升模型计算混凝土的水化热，并对大体积混凝土的施工过程进行温度场及温度应力仿真计算分析研究。常用的绝热温升模型有双曲线、指数以及复合指数的型式[11]。事实上，随着目前计算力学以及计算机技术的发展，基于绝热温升模型的大体积混凝土温控仿真算法已经比较成熟[12-14]。然而，绝热温升模型虽然易于在有限元方法中实现，但该模型缺乏从本质上对混凝土材料化学反应特性的认识。

结合混凝土水化反应的物理-化学变化本质、化学反应动力学及热力学基本理论，推导了一种描述混凝土水化过程水化反应程度与温度及时间关系的水化度模型，并给出了其在有限元法中的实现过程。该模型可为预测混凝土水化放热过程提供新的手段。

1 基本理论

1995年，Ulm[3]等基于多孔介质化学反应及传热传质的理论框架，将混凝土看作是由骨料骨架和孔隙构成的多孔多相介质，并认为水化反应的机制是水分在水化产物中的扩散。水泥浆体中存在很多连通的毛细孔，这些毛细孔是水分扩散的通道。自由水从外层的水化产物中的毛细孔扩散，当遇到未水化的胶凝材料时，会与胶凝材料发生化学反应，形成新的水化产物，整个过程如图1所示。

图1 水泥水化过程中自由水扩散示意图Fig.1 The diffusion of free water during cement hydration

混凝土水化反应过程中各种物理变化均来源于化学反应，实质上是自由态的水分与各种不稳定的脱水氧化物结合的过程。在封闭的化学反应系统的假设下(即反应中无外部补充水分或损失水分)，可引入水化程度作为反应系统的内部变量。在此条件下，热化学反应系统的自由能可以表示为两个变量的函数，一个为外部变量(温度)T，一个为内部变量(水化程度)χ：

ψ=ψ(T,χ)=V(T)+L(T,χ)+H(χ)

(1)

表达式中V(T)代表热能部分：

(2)

式中：T0为初始温度；C为单位体积比热容(在无压力的试验下)。

热化学耦合部分可表示为L，表达式为：

(3)

式中：Q(χ)代表单位体积反应物热量的释放，Q(χ)为反应进行程度的函数。多数学者认为放热速率与水化速率相关，可以等价认为Q(χ)与χ为线性关系：

Q(χ)=Qχχ

(4)

式中：Qχ代表单位水化程度混凝土的潜热，可以被认作材料常数。

最后，H(χ)代表化学能，是一个关于水化程度χ的函数。笔者在文献[15]和[16]中提出一种水化度模型公式，事实上，该模型是基于H(χ)为χ的四次函数的假设：

H(χ)=

(5)

式中：β1,β2以及β3均为材料参数；χ∞为水化过程结束χ的最终值，即χ能达到的最大值。

由科尔曼方法，可以从方程(1)得到状态方程：

(6)

Aχ=-∂χψ(T,χ)=β1(β2+β3χ+χ2)(χ∞-χ)-∂χL

(7)

式中：S为反应系统的熵变；Aχ为反应的化学亲和力，代表温度和化学反应程度的共轭力。

在混凝土通常所处环境的温度范围内，式(7)的最后一项，-∂χL通常可忽略不计。化学能的耗散可用以下公式表示：

(8)

(9)

式中：Ea表示反应活化能；R为理想气体常数；ηχ为自由水在已水化产物中的黏度。

混凝土Ea/R为的比值可以通过试验来测定，其范围在3 000～8 000 K，通常为5 000 K左右。

黏度ηχ为关于χ的函数，随水化的进行，未水化的水泥颗粒外部包裹的水化层厚度不断增加，自由水扩散到未水化水泥颗粒的时间也随之增长。ηχ表达为：

(10)

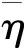
(11)

显然，式(11)可以满足不等式条件。将式(10)代入式(9)得到：

(12)

为了便于实际应用，引入水化度的概念描述水化反应进行程度，将其定义为反应中结合水占总的水分的体积分数。为方便实际应用，通常将其改写为标准化的变量：

(13)

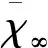
(14)

基于方程(4)的线性化假设，Q(ξ)=Qξξ。因此，水化度也可以定义为：

(15)

化学能可以改写为：

(16)

水化反应速率(水化度对时间的导数)为：

(17)

2 方法的实现

2.1 混凝土瞬态热传导过程

热传导平衡方程可以用方程(18)、(19)来描述：

(18)

对于各向同性的情况：

λx=λy=λz

(19)

混凝土为各向同性热传导，水化过程可视作有内热源，瞬态热传导过程可按下式描述：

(20)

(21)

式中：ρ,C,λT,△和Q∞分别为密度，体积热容量，导热系数，拉普拉斯算子以及最终单位质量水化热。

由于混凝土温度水平影响其水化热的释放，因此，由水化造成的混凝土潜热的释放实质上是非线性且热相关的过程。

2.2 化学-热耦合模型在有限元法中的实现

方程(20)和(21)列出了水化放热以及瞬态热传导方程；为了在有限单元法中实现热-化学耦合，时间积分采用隐式欧拉向后积分的方法，空间积分采用高斯求积方法。在t+δt(δt指时间增量)时刻，可将这些方程离散化如下：

(22)

(23)

因此, 水化方程可以转化为

(24)

(25)

基于虚功原理，基本热传导能量平衡方程可以表示为

(26)

结合方程(22)和(23)可推出：

(27)

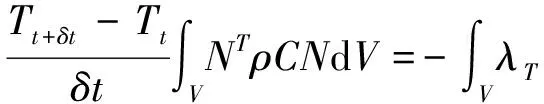
(29)

式中：N为形函数矩阵；上标T指代矩阵或向量的转置；K和C分别为导热和比热矩阵。在每个时间增量内，耦合方程(28)和(29)可以用来求解水化场以及温度场。为了形成Q矩阵，ξt+δt必须在方程(25)中求解；因此，本文采用牛顿-拉普森(Newton-Raphson)迭代方法求解。在隐式时间积分方法中，节点温度以及水化度的求解可由以下步骤完成：

(1) 输入变量：δt,Tt,ξt,Kt和Ct。

(2) 设置合适的时间增量值并初步计算Tt+δt的值。

(3) 采用牛顿-拉普森迭代方法求解ξt+δt的值:

(30)

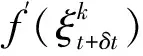
(4) 分别计算Q,Kt+δt以及Ct+δt矩阵，并验证方程(29)的平衡性。如果方程(28)可以达到平衡状态，那么继续下一步，即步骤(5) ；否则返回步骤(2)并重新调整温度增量值。

(5) 输出变量值:Tt+δt,ξt+δt,Kt+δt以及Ct+δt。

2.3 水化模型参数的反演

确定合理的模型参数是数值模拟中的重要环节。水化度模型的相关参数可通过物理试验数据进行反演。目前，通常在绝热条件下测量混凝土的温度或水化放热量来推求水化动力学参数[18]，主要由以下方程得到：

(32)

(33)

式中：Q为水化放热量；Q∞代表混凝土完全水化放热量；ξ(t)指水化度；t0代表诱导期结束的时间；t0.5指水化度到达0.5的时刻。

已知混凝土水化放热量的条件下，结合式(32)和(33)，可通过与试验数据对比的方法获得水化度模型的各个参数。

3 实例分析

3.1 不同初始温度的绝热试验

采用本文中的计算方法，结合试验数据，将不同水胶比(w/b)的混凝土试件在绝热试验下的温度试验值和模拟值绘制于图2和图3。结果表明水化度模型模拟温度值与试验结果相吻合。最终，得到两组不同水胶比的混凝土水化度模型参数见表1。

表1 不同水胶比混凝土水化度模型参数Tab.1 Hydration model parameters of concrete with various water-binder ratio

在得出水化度模型参数后，为直观反映温度对水化过程的影响，分别对初始温度为10、15、20 ℃的混凝土试件进行绝热试验的数值模拟，并将温度历程曲线绘制于图2和图3，将水化度历程曲线绘制于图4和图5。由图中可以看出，不同的温度条件下，混凝土温度上升速率也不相同：初始温度为10 ℃的混凝土1 000 h的绝热温升为17.5 ℃，而25 ℃的混凝土绝热温升达21 ℃。造成温度历程不同的根本原因是水化度随时间的演化受温度的影响。

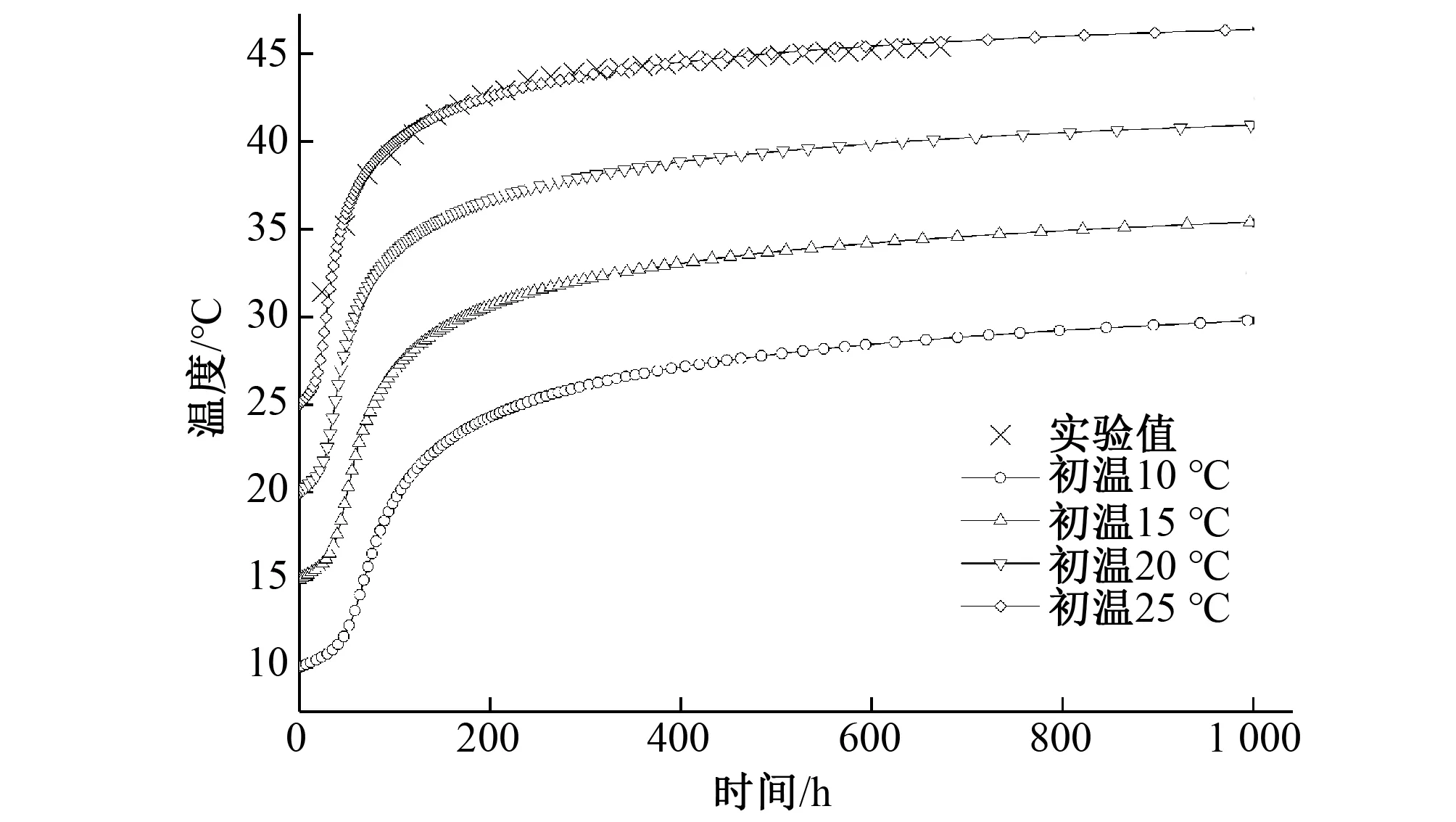
图2 不同初始温度混凝土绝热温升(w/b=0.45)Fig.2 Adiabatic temperature rise of concrete with various initial temperature (w/b=0.45)

图3 不同初始温度混凝土绝热温升(w/b=0.48)Fig.3 Adiabatic temperature rise of concrete with various initial temperature (w/b=0.48)

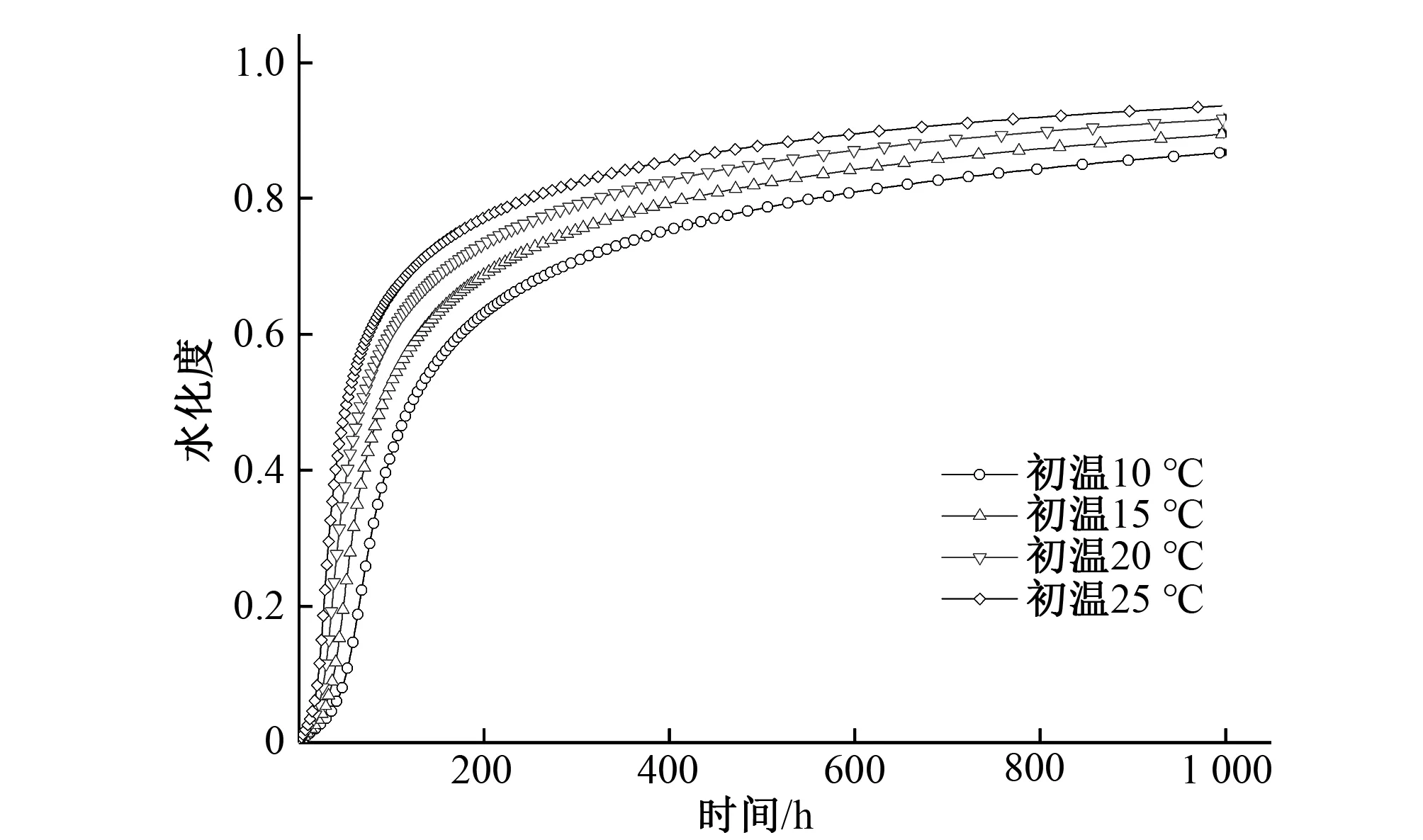
图4 不同初始温度混凝土水化度发展历程(w/b=0.45)Fig.4 Hydration evolution of concrete with various initial temperature (w/b=0.45)

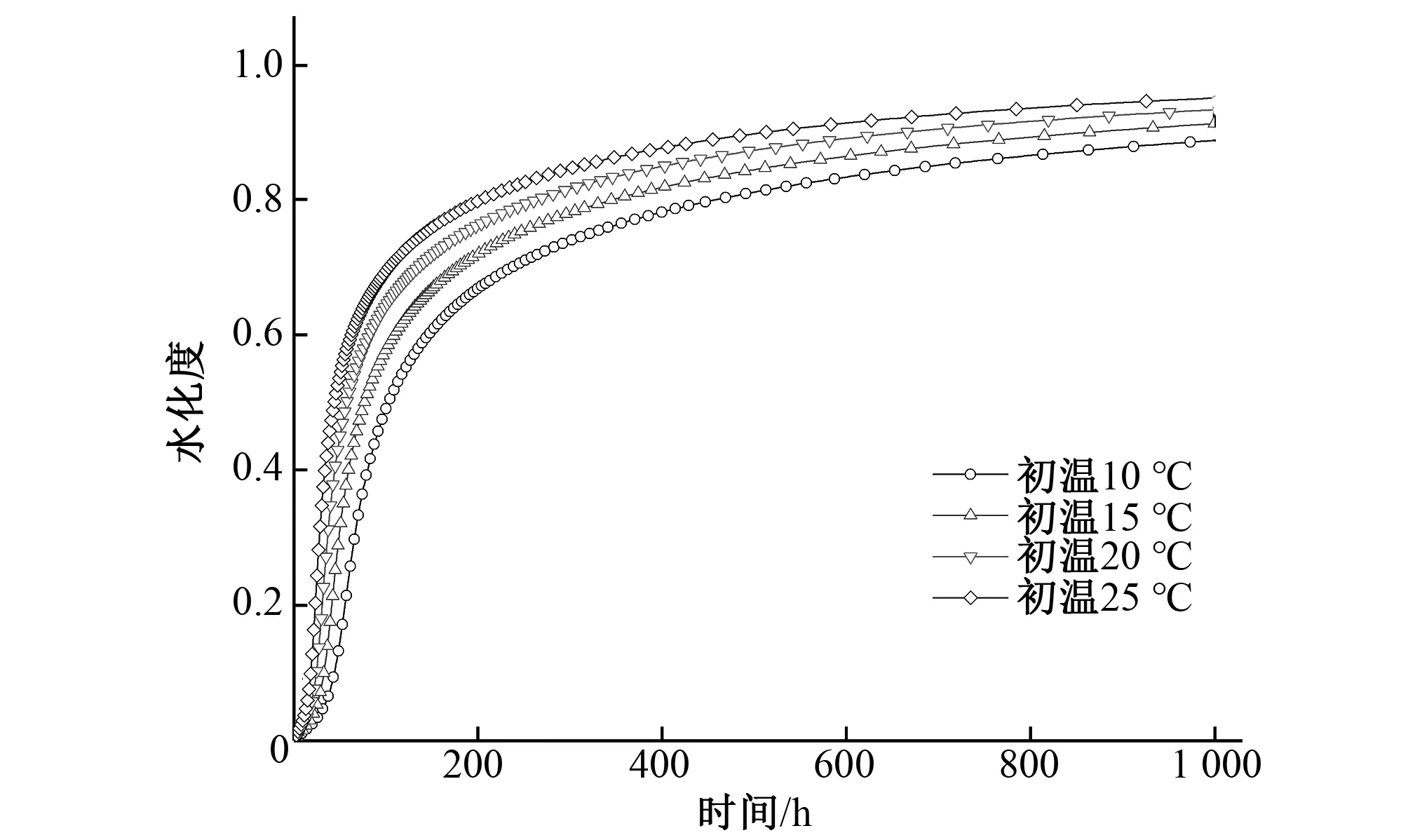
图5 不同初始温度混凝土水化度发展历程(w/b=0.48)Fig.5 Hydration evolution of concrete with various initial temperature (w/b=0.45)

3.2 大体积混凝土的热-化学耦合现象

为研究大体积混凝土结构内部的热-化学耦合现象，本文建立了一个简单的混凝土浇筑块的二维模型并简化边界条件进行数值模拟。混凝土浇筑块大小为20 m×3 m，采用上节的水胶比0.45的大坝混凝土，取地基范围为60 m×10 m。地基以及混凝土与空气直接接触部位均采用对流边界，外界气温取为恒温20 ℃，取热交换系数为47 kJ/( h·m2·℃)，地基和浇筑块初始温度均取为25 ℃。

图6、图7和图8分别为3、7和28 d龄期混凝土浇筑块温度及水化度的分布图。图中可直观看出，大体积混凝土结构的水化发展过程呈现明显的空间不均匀的特性，结构内部水化程度较表面部位的水化程度高。

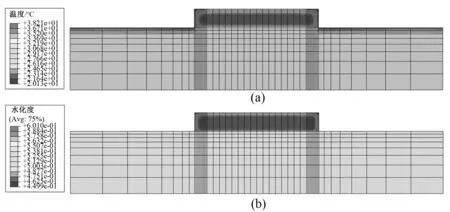
图6 3 d龄期混凝土浇筑块温度及水化度分布情况Fig.6 The temperature and hydration distribution of concrete slab at the age of 3 d

图7 7 d龄期混凝土浇筑块温度及水化度分布情况Fig.7 The temperature and hydration distribution of concrete slab at the age of 7 d

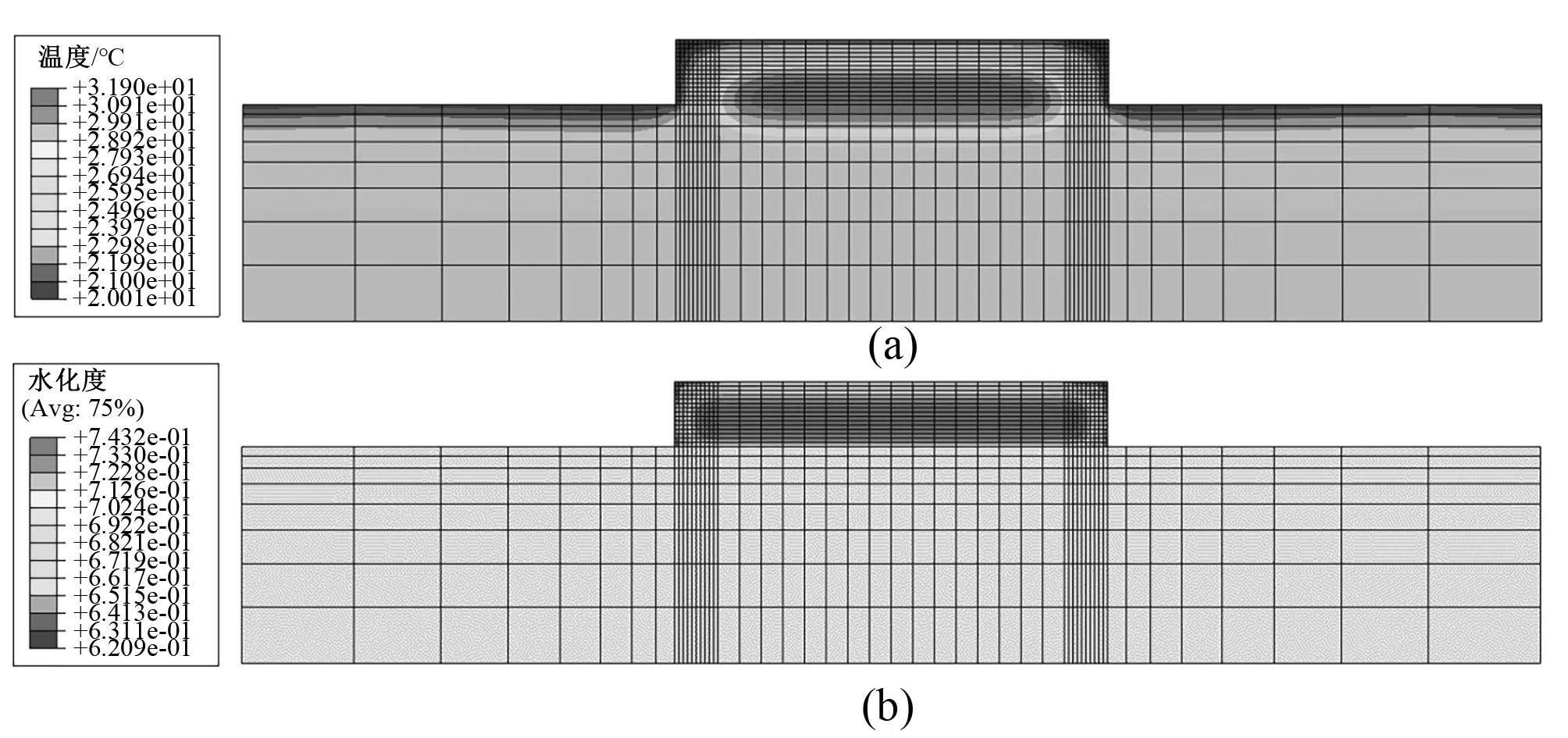
图8 28 d龄期混凝土浇筑块温度及水化度分布情况Fig.8 The temperature and hydration distribution of concrete slab at the age of 28 d

选取混凝土浇筑块中间高程的表面点和内部点作为代表点，绘制两代表点温度及水化度发展历程曲线如图9和图10所示。由于散热条件不同而导致的大体积混凝土结构内外温度历程的显著差异，其对应的水化发展过程也不同。

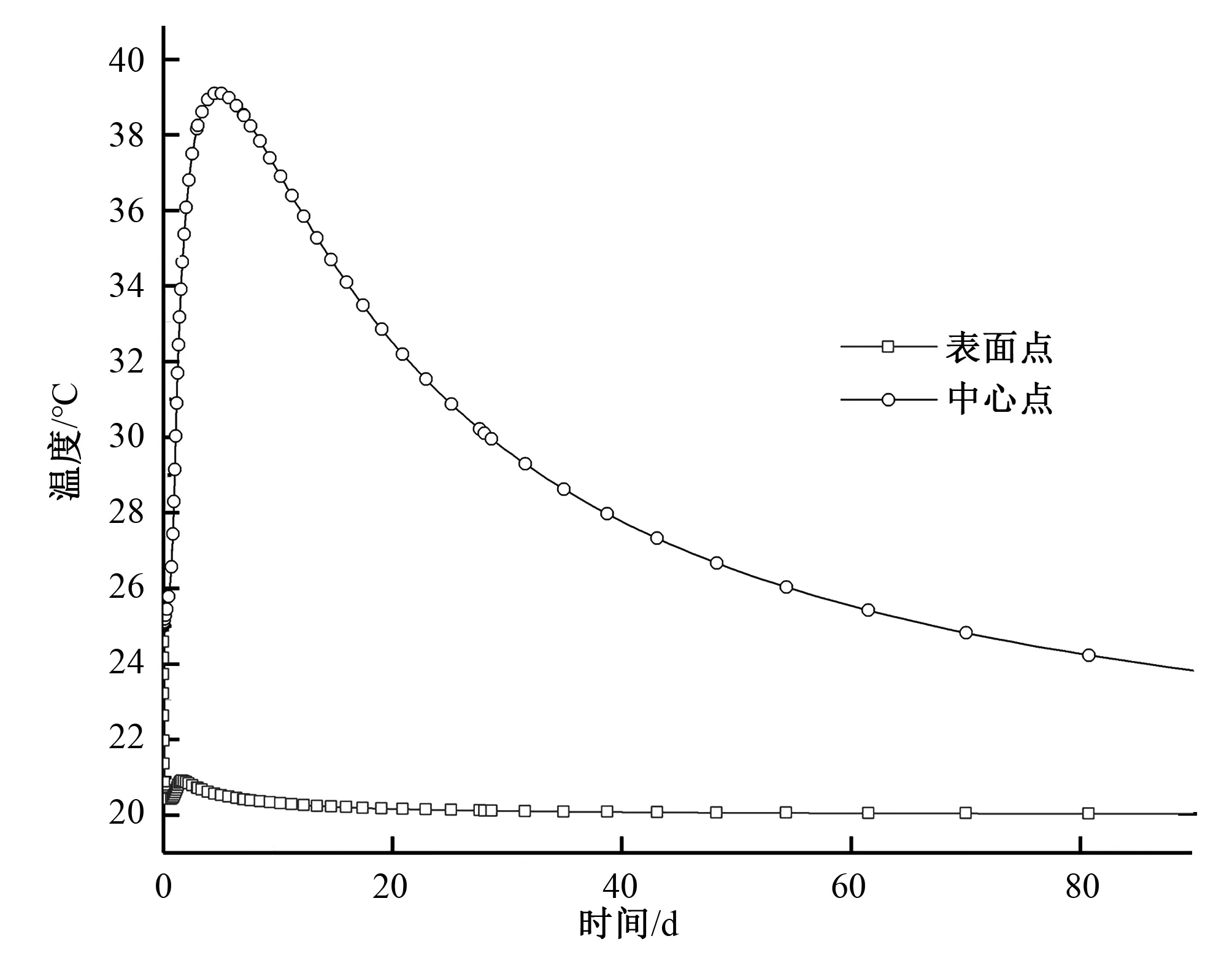
图9 代表点温度发展历程对比图Fig.9 The temperature evolution of representative points

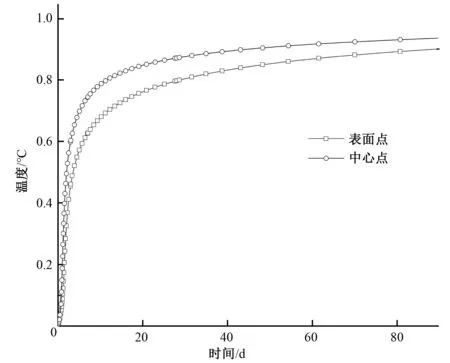
图10 代表点水化度发展历程对比图Fig.10 The hydration evolution of representative points

4 结论与展望

本文基于热力学及化学反应动力学的基本理论，推导了一种水化度模型，并利用有限元方法实现该模型。数值模拟结果对比试验数据表明，水化度模型模拟值与试验结果吻合良好。此外，本文通过对不同初始温度的混凝土的绝热试验进行数值模拟，揭示了混凝土水化过程中温度场的变化受自身约束的特性。基于本文的主要工作，提出结论总结以及相关展望如下：

(1)本文的研究可为探讨混凝土性能演变机理的提供理论参考，混凝土内部化学反应程度是影响混凝土各项力学性质的关键环节，从定量角度对其进行深入研究无疑具有重要意义。

(2)对于混凝土初始温度相差不大(5～15 ℃)的情况下以及相同初始温度的大体积混凝土内部及表面部位，水化过程差异已经较为明显。由于水化过程与混凝土强度发展密切相关，因此，对于散热条件较差而导致内外部温差较大的大体积混凝土结构，结构内外部水化过程可能存在更显著的差异，这种现象需引起重视并开展深入研究。

(3)工程上常用预埋冷却水管对大体积混凝土结构进行通水冷却，常用的仿真算法是以经验公式为基础的。结合本文的计算结果，可以认为，当前的包含冷却水管的混凝土温度场仿真之所以满足工程精度，可能由于现有的水管冷却计算方法也存在一定偏差，两者误差有一定程度的抵消。鉴于水管冷却效应求解的复杂性(事实上，该问题是一个典型的流固耦合问题)，联立混凝土的热化学耦合问题，难以求得解析解。因此，笔者将结合传热学方法及一些基本假设，在下一步的研究中，对该问题的数值解法进行深入探讨。