基于支持向量机方法的土壤水分特征曲线预测模型

李彬楠，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

土壤水分特征曲线是土壤水吸力与含水率的关系曲线，反映土壤水数量与能量的关系。针对土壤水分特征曲线国内外的专家学者们进行了大量的研究，赵雅琼[1]等研究了土体的粒径状况对土壤水分特征曲线的影响；谭霄[2]等分析土壤盐分对水分特征曲线的影响，分析得到随着含盐量的增加偏移幅度减少且盐分种类对土壤水分特征曲线的影响没有明显规律；高慧嫣[3]等对重土壤、中土壤和轻土壤等5种不同质地土壤的水分特征曲线进行比较分析，得到了其土壤水分特征曲线及其参数的变化规律。同时专家们也提出不少表征土壤水分特征曲线的模型，常用经验模型有Gardner模型[4]、Gardner-Russo模型[5]、Frdlund and Xing模型[6]、Van-Genuchten模型[7]等。目前由于Van-Genuchten模型适用于多种质地的土壤、模型稳定性强、预测精度高，因此被人们广泛应用。

1995年Cortes等人提出支持向量机，是基于统计学习理论的VC维理论和结构风险最小原理。支持向量机有其特有的优势，因此在诸多领域中被广泛应用。李晓婷[8]等运用支持向量机模型进行土壤重金属污染评价并与Hakanson指数法和内梅罗综合污染指数的评价结果进行对比，得到支持向量机的评价结果更为准确；刘文霞[9]等讨论了基于相似日的支持向量机电动汽车日负荷预测方法，结果表明与其他预测方法相比，此法具有较高的预测精度和稳定性；黄化坚[10]采用支持向量机计算高土石坝坝坡稳定可靠度，结果表明该方法简便，精确度高，实用性强，结果具有较高的工程应用价值。但是，鲜有文献运用支持向量机对土壤水分特征曲线进行预测，因此本文借助此方法建立以黄土高原区土壤基本理化参数为输入变量，以土壤水分特征曲线Van-Genuchten模型参数为输出变量的支持向量机预测模型，为研究土壤水分特征曲线提供了更多的理论基础。

1 材料与方法

1.1 土壤状况

试验区域位于山西省交城县、临县及离石区等多个县区。试验区的土壤质地、干容重、有机质、全盐量等土壤理化参数指标丰富多样，建模的数据库具有代表性，选取试验点的土壤理化参数见表1。

表1 试验区内各项土壤理化参数表

1.2 试验内容

(1)试验测定项目：土壤质地、容重、有机质含量、全盐量、土壤水分特征曲线的测定。

(2)主要试验器械：1500F型压力膜仪(美国制)、Rise-2022型激光粒度分析仪、化学试验器材。

(3)试验方法：土壤质地使用激光粒度分析仪测定；人为配制1.0～1.7 g/cm310个不同梯度的密度；有机质含量用重铬酸钾容量法进行测定；盐分用化学法进行测定；土壤水分特征曲线使用压力膜仪测定，将装有土样的环刀放到压力膜仪中，加入水使土样吸水饱和，24 h以后对进行土样饱和含水率的测定。然后按照0.3、0.6、1、3、6、8、12和15 bar压力值对土样进行加压，土样由于受压将水排出，并且每隔同样的时间测定土样的重量。8个压力值完成后测定干容重值并计算体积含水率，最终获得不同水吸力值下的土壤含水率得到土壤水分特征曲线的模型参数。

1.3 Van-Genuchten经验模型

土壤水分特征曲线Van-Genuchten模型结构如下：

(1)

式中：θ为体积含水率；θs为饱和含水率；θr为残余含水率，m3/m3；h为压力水头，m；m、n是曲线形状参数，m=1-1/n。n表示曲线的坡度，当n较小时曲线较缓；当n较大时曲线较陡。α是与进气值有关的参数，m-1，表示土壤进气值大小，一般黏土进气值较大，砂土的进气值较小，甚至接近于0。

2 建立支持向量机Van-Genuchten模型参数的预测模型

2.1 模型输入与输出参数的确定

通过土壤水分特征曲线试验，研究土壤基本理化参数与模型参数之间的单因素影响，分析得知土壤质地、容重、有机质、全盐量对Van-Genuchten模型参数α与参数n具有明显的影响。

(1)参数α影响因素分析。参数α表示土壤初始排水的难易程度。土壤质地的差异性表现在土壤体系孔隙状况的不同，随着黏粒含量的增加土壤水吸力增强，土壤初始排水的难度逐渐增大；土壤密度的变化是由土壤孔隙和土壤固体决定的，大孔隙越少中小孔隙越多土壤的密度越大，则土壤初始排水的难度增大；土壤有机质影响土壤胶体与结构状况，土壤吸水能力随其含量的增加而增强，导致土壤初始排水的难度增大；土壤盐分影响着土壤水吸力的大小，盐分含量越高水吸力越强，使得土壤初始排水的难度增大。

(2)参数n影响因素分析。参数n表示土壤水分特征曲线的坡度情况。土壤质地越重其黏粒含量越多，进气吸力值随之减小，土壤水分特征曲线弯曲度小从而坡度变缓；土壤容重增加土壤的结构更加紧实，从而影响进气吸力值使得曲线坡度变小；土壤有机质和盐分的含量引起土壤水吸力的变化，水吸力越大土壤初始排水越难，最终导致土壤水分特征曲线的坡度变缓。

综上可知，土壤质地、干密度、有机质和全盐量对参数α、n都有影响，所以以黏粒含量、粉粒含量、干密度、有机质含量、全盐量5个因子作为预测模型的输入参数。 根据上文所述可知Van-Genuchten模型有4个参数，饱和含水率和残余含水率可以通过室内实验获取，但经验参数α、n不可以，从而采取土壤传输函数法获得，由此确定输出参数为参数α、n。

2.2 支持向量机原理简介

Xi(i=1，2，3,…,n),Xi∈Rm为输入的训练样本；Yi(i=1，2，3,…,n)，Y∈R为输出的对应期望。两类样本被一个超平面彻底分开，最优超平面的形式表示如下：

Y=f(x)=ωφ(X)+p

(2)

引入不敏感损失函数ε，运用离差分析对最优超平面进行求解，当ε大于误差值时，则误差小可忽略不计；引入松弛变量ξ与ξ*，目的是预防个别数据影响模型偏差；引入惩罚因子C，惩罚偏离模型的样本数据，因此最优超平面可转换成式(3)和式(4)求解最小值的问题：

(3)

(4)

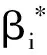
(5)

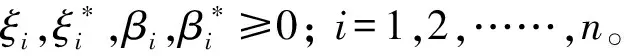
(6)

将公式(6)联立求解，引入非线性核函数得到支持向量机的回归函数。常用的核函数包括Sigmoid核函数、多项式核函数和高斯核函数，本文采取第三种即高斯核函数来建立预测模型，其形式表现如下：

(7)

结合式(6)和式(7)，最终确定最优超平面的形式如式(8)所示。

(8)

式中：K(x，xi)为支持向量机高斯核函数。

2.3 确定支持向量机回归参数

在支持向量机回归算法中，参数取值的选择十分重要，直接决定了模型的泛化能力和预测精度。惩罚因子C和核参数g是影响支持向量机学习能力的主要参数。

惩罚因子C的值和可容忍误差相关，是样本误差与结构风险的折中。C值愈大允许误差愈小，且数据拟合度愈高但可能过拟合；C值愈小允许误差愈大，则可能不符合训练与预测精度的标准。核参数g与学习样本的输入空间范围相关，其值随输入空间范围的增大而增大。本文采用网格搜索法对两个参数的取值进行优化。最终选取C=20，g=20。

3 Van-Genuechten模型参数支持向量机精度分析

3.1 支持向量机模型精度分析

以80组数据作为建模样本进行训练，利用支持向量机模型对参数α进行预报训练， 其实测值与预测值对比分析见表2和图1。

表2 模型参数α预测结果与误差检验

图1 模型参数α拟合效果图

从表2和图1可知，参数α的实测值与预测值之间的误差较小，相对误差的最大值为24.74%，最小值为0.33%，平均相对误差为3.94%，R2=0.985 3，除个别实测值有较大的误差以外，其余的实测值均取得了理想的预测值，说明基于支持向量机建立的模型参数α具有较高的精确度。从拟合效果图来看，参数α的建模样本取得良好的预测效果。

对参数n的80组建模样本采取同样的程序进行预测，其实测值与预测值对比分析见表3和图2。

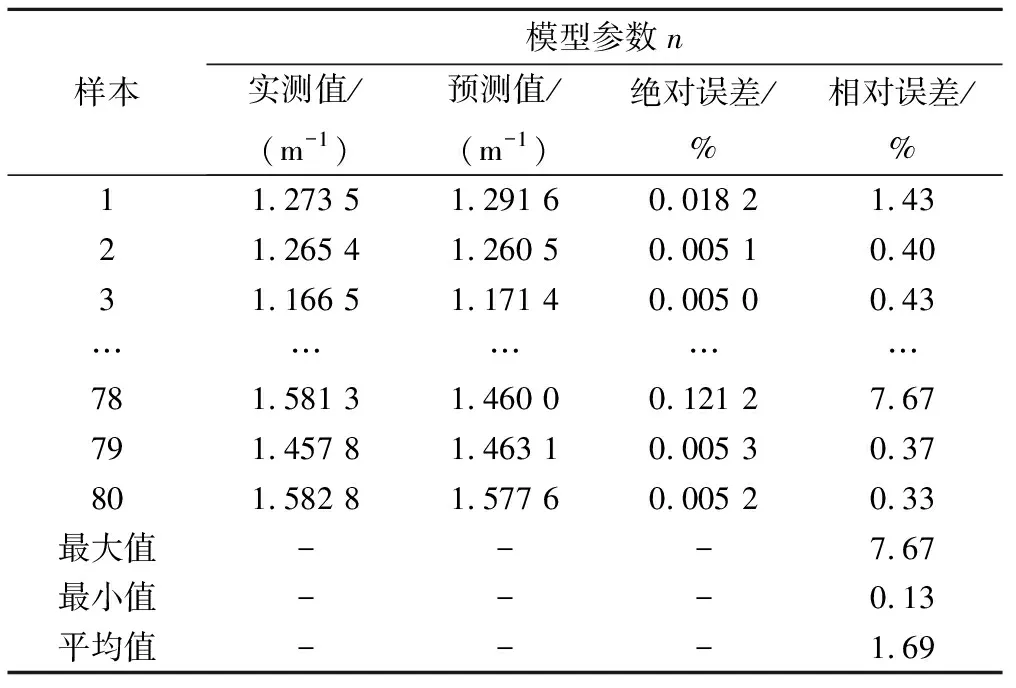
表3 模型参数n预测结果与误差检验

图2 模型参数n拟合效果图

从表3和图2可以看出，参数n的实测值与预测值之间的误差小，其中相对误差的最大值仅为7.67%，最小值为0.13%，平均相对误差为1.69%，R2=0.986 8。说明支持向量机模型对参数n的预测精度高。从拟合效果图来看，参数n的建模样本训练效果好，具有理想的预测效果。同时，对比参数α和参数n建模样本的精确度和拟合效果，发现参数n精确度更高，模型拟合效果也更好。

3.2 模型参数检验样本精度分析

(1)参数α检验样本精度分析。用预留的8组数据样本检验本文所建立的支持向量机预测模型的精确度，获得Van-Genuechten模型参数α验证样本的相对误差分析见表4和图3。

表4 参数α验证样本相对误差表

图3 参数α验证样本拟合效果图

对参数α的检验样本进行误差分析，从表4和图3可知，相对误差的最大值为8.51%，最小值为1.61%，平均相对误差为3.65%，R2=0.992，验证样本比建模样本的平均相对误差3.94%还要小，结果说明建立的支持向量机模型具有较高的精确度以及良好的预测效果。因本文采用的建模样本以及验证样本均是小样本数据，且Van-Genuechten模型参数α与土壤基本理化参数之间有着高度的非线性关系，从而达到了高精确度和理想的预测效果。因此，在本文所建立的支持向量机模型下，参数α与土壤基本理化参数之间的土壤传输函数是可行的，且该模型用来预测小样本及非线性问题具有很大的优势。

(2)参数n检验样本精度分析。同样用预留的8组数据样本检验参数n在本文建立的支持向量机模型下的预测精度，最终预测结果与相对误差分析见表5和图4。

表5 参数n验证样本相对误差表

图4 参数n验证样本拟合效果图

从表5中可以看出，参数n的验证样本相对误差的最大值为5.90%，最小值为0.30%，平均相对误差为1.29%，R2=0.951 3，检验样本比建模样本的相对误差值要小，说明在建立的支持向量机模型下，参数n的预测精度高且验证结果良好。

通过比对参数n、α的预测精度，发现参数n具有更高的精确度。综合分析原因可能是参数n的变化范围相对较小，其均处于同一数量级即1～2之间，而参数α基本是小于1的数，其最大值和最小值可相差一个数量级，容易受到输入参数即土壤基本理化参数的影响，导致波动较为明显，因此参数n的预测精度比参数α的高，稳定性也更强。

4 结 语

(1)建立以土壤黏粒含量、粉粒含量、密度、有机质、全盐量为输入参数，Van-Genuchten模型参数α和n为输出参数的支持向量机模型，同时对所建模型的精度和拟合效果进行比较和分析，结果表明Van-Genuchten模型参数支持向量机的预测模型具有优异的预测效果。其中，从建模样本来看，参数α平均相对误差为3.94%，参数n平均相对误差为1.69%；从检验样本来看，参数α平均相对误差3.65%，参数n平均相对误差1.29%，结果表明Van-Genuchten模型参数α、n的预测精度均较高，说明运用支持向量机模型预测小样本和非线性问题是可行的。

(2)在支持向量机模型中，对样本数据进行预测时个别数据出现较大的误差，综合分析造成误差的原因如下：样本数据库容量的大小，建立模型时对于支持向量机核函数的选择等众多影响因素有关。此后，在此基础上对于支持向量机模型的建立进行不断的优化已解决可能出现的问题，以便达到预期的预测效果，更加符合实践活动中的实际状况。