基于HYDRUS模型筛选滴灌模式下适宜灌水上下限的研究

杨昊晟，艾一丹，格宇轩，邢 正，白雪儿，胡笑涛，周始威

(西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

0 引 言

我国是一个水资源贫乏的国家[1]，农业作为用水大户[2]，农业节水势在必行。在干旱半干旱地区，滴灌作为一种节水效果显著的局部灌溉方式被广泛采用。滴灌灌水定额的确定需要综合考虑土壤水分上、下限，计划湿润体及计划湿润比等因素。在实际生产中，通常将田间持水量(θFC)作为灌水上限。然而，有研究表明以田间持水量为灌水上限指导灌水会使部分灌溉水(10%～15%)渗入计划湿润体以外成为较难利用水分[3]，造成水资源浪费。可见，以田间持水量为灌水上限并不合理。理想的灌水上限应当使灌溉水尽可能多的分布于计划湿润体，且湿润体内含水量适宜作物生长。而现有研究多以作物产量，品质及水分利用效率确定适宜的灌水上限，对不同灌水上限下灌溉水于土体中的分布情况未作重点讨论。灌水下限的确定更多的是考虑作物的耐旱，抗旱能力,作为灌水的初始含水量，灌水下限也会影响到灌水效果。在理论上，不同的灌水下限所对应的理想灌水上限也不同。在确定灌水上限时，需要对不同灌水下限单独加以讨论。张俊以扰动土为研究对象,采用室内试验方法探究了不同初始含水率条件下微润灌土壤水分分布的变化规律[4]。但室内难以进行大量滴灌试验，拟采用数值模拟与室内试验结合的研究方法。当前，HYDRUS在模拟土壤水分运移中应用广泛，周广林等通过HYDRUS3D模型模拟单点源情况下水分入渗及其再分布过程,验证评价了HYDRUSD模拟土壤水分运移的准确性[5]；何小梅利用HYDRUS探讨了灌水量对滴灌土壤中水分运移的影响[6]。还有不少学者都应用HYDRUS在土壤水分运移方向取得了较好的模拟结果。

1 材料与方法

1.1 试验区概况

试验在西北农林科技大学旱区农业水土工程教育部重点实验室进行。旱区农业水土工程教育部重点实验室位于杨凌西北部，黄土高原南部旱作区。该站位于东经108°24′，北纬34°20′，海拔高度为521 m。此区多年平均气温为14.5 ℃，年平均降雨量约为635～665 mm，主要集中在7月份到9月份，属于半湿润易干旱地区。年累积日照时数约1 900 h，年累积气温(超过10 ℃)3 800 ℃，年蒸发量在900～1 100 mm之间[7]。供试土壤取自渭河杨凌段滩地，取土深度为0～40 cm。土壤容重为1.35 g/cm3，过2 mm筛后，使用马尔文粒度仪2000测量土壤的机械组成为砂粒(0.02 mm以上)占81.42%，粉粒(0.002～0.02 mm)占17.64%，黏粒(<0.002 mm)占0.94%，属于沙壤土。

1.2 试验设计与方法

试验由室内滴灌试验与HYDRUS模型模拟试验组成,以室内实测数据评价该模型对土壤水分运移模拟的精度。

1.2.1 试验装置与方法

室内滴灌试验装置由圆形土桶、供水系统及量测系统组成。圆形土桶的材质为均质铁皮，规格为R=35 cm、H=50 cm。试验采用长圆柱形马氏瓶进行供水，马氏瓶上张贴标尺可对灌水量进行量测。

试验前将土样自然风干，过2 mm筛，通过烘干法测定风干土含水率，依据试验设计人工拌和配置一定初始含水率土壤。按干容重1.35 g/cm3分层(每10 cm一层)装入土桶，层间打毛，测定田间持水量为23.47%(质量含水率)。装土同时埋入ECH2O传感器(美国Decagon公司，精度±1%)，在土体中按10 cm×10 cm网格在湿润体断面布置传感器，分别埋于土层深度为3、13、23、33、43 cm处，每层沿径向布设探头4个，分别距离滴头0、10、20、30 cm，共布置20个，如图1。设置ECH2O每隔1 min自动记录一次测点含水率,试验结束后用取土烘干法进行校正。滴头安装于φ16 mm毛管上，位于土桶中心。试验前先打开毛管旋钮开关让水流充满以便排气，待水流稳定后，利用秒表和容量瓶测定实际滴头流量。试验中土表面覆膜。

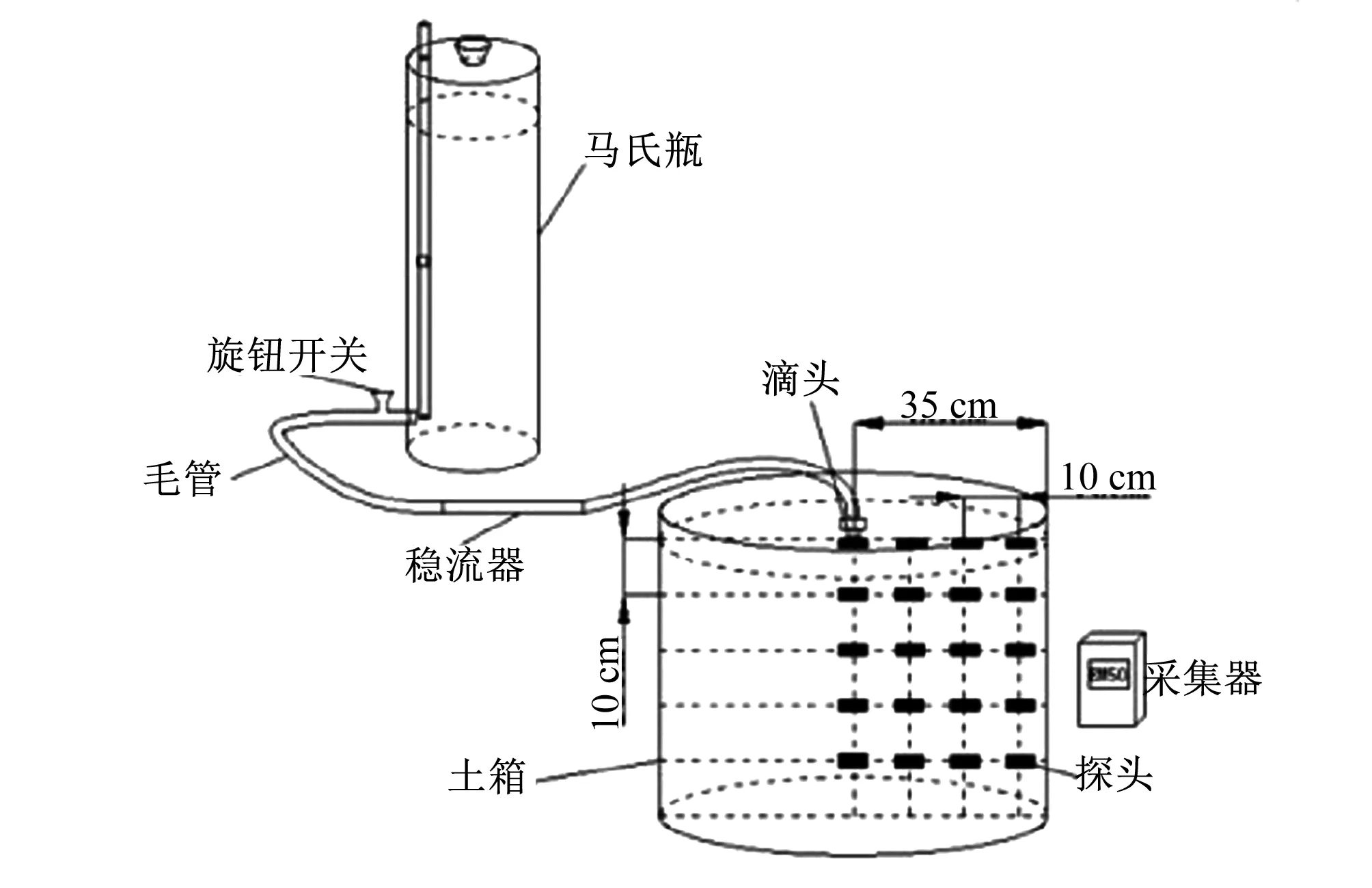
图1 室内滴灌试验装置示意图

1.2.2 试验设计

室内试验为不同滴头流量和不同土壤初始含水率的二因素试验，滴头流量与初始含水率以实测值为准。流量分别为1.1、4.9 L/h；土壤初始含水率53%θFC，66%θFC。完全组合共4组处理。滴灌试验过程中灌水上限均设置为100%θFC，灌水量采用下式计算：

M=γV(θ上-θ下)

(1)

V=pdbh

(2)

式中：γ为土壤容重，1.35 g/cm3；θ上为灌水上限；θ下为灌水下限；p为设计湿润比，本次取值为0.65；V为计划湿润体体积；d为滴头间距，取30 cm；b为毛管间距，取40 cm；h为计划湿润土层深度，取50 cm。

在模拟试验设计中，固定滴头流量为2.0 L/h。设置不同灌水下限和不同灌水上限的二因素完全组合试验(表1)。

表1 HYDRUS模拟试验设计表

2 HYDRUS模型

2.1 土壤水力学运动方程

在配置一定初始含水率的土壤时对土样进行了充分搅拌，认为土壤均质且各向同性。土壤水分运动过程符合达西定律和质量守恒定律，按照轴对称问题处理，此时Richard方程变为：

(3)

式中:D(θ)为土壤扩散率；k(θ)为土壤导水率；Z坐标向下为正。

土壤水分特征曲线采用Van Genuchten模型拟合：

(4)

(5)

其中：

(6)

(7)

式中：θr为土壤残余含水率，cm3/cm3；θs为土壤饱和含水率，cm3/cm3；K为饱和导水率，cm/h；h为土壤负压水头，cm；α为土壤形状参数；n为土壤进气值的倒数；l为孔隙连通性参数，一般情况取平均值0.5[8]；Se为土壤水分有效含水率，cm3/cm3。

本次试验土壤水动力学参数利用HYDRUS反演模块推求，结果见表2。

表2 HYDRUS模型反演土壤水动力学参数

2.2 模拟设置

以含水率为初始条件。模拟几何类型采用2D-Axisymetrical Vertic。模拟中忽略土壤温度以及土壤水分数量和能量关系的滞后效应对土壤水分运动的影响。对称轴为土桶中心线。点源设置为半径为Rs的圆弧线，为变流量边界，Rs为滴头周围土壤饱和区半径。上边界其余部分与试验土表面对应，设置为无流量边界。右边界与下边界为桶壁，设置为无流量边界。左边界为对称轴，可按照无流量边界设置。如图2。

图2 边界条件

模型点源处滴灌流量参数是用流量除以饱和积水区半球体表面积。李久生[9]的研究表明，饱和区域的半径与流量和土壤质地有关，本试验得到的饱和区域积水半径与流量的幂函数关系为：

r=26.79q0.03

(8)

式中：r为饱和区域积水半径，mm；q为滴头流量，L/h。

2.3 率定情况

率定通过土壤剖面含水率实测值与模拟值随时间变化的对比进行验证，在模拟剖面与室内试验剖面探头同位置处设置观测点[10,11]，同时考虑到水分运移在空间与时间上的分布。调整HYDRUS模拟初始步长、最小步长和最大步长均为1 min,与ECH2O每隔1 min记录一次数据保持一致。

率定基于均方根误差RMSE与决定系数R2：

(9)

(10)

4组处理20个观测点R2均值为0.83，RMSE均值为0.034，表3给出4个观测点处含水率动态变化的实测及模拟值比较结果。模拟精度满足研究需要。

注：观测位置为(径向距离，土层深度)。

3 模拟试验结果与分析

3.1 不同灌水下限滴灌湿润体水分分布特征

以100%θFC作为灌水上限， 50%θFC、60%θFC、70%θFC作为灌水下限,模拟灌水结束时湿润体水分分布情况如图3。三个处理形成湿润体体积之比为1∶1.09∶1.12，均有灌溉水入渗到计划湿润体以外，以50%θFC为灌水下限时湿润体体积与计划湿润体体积最为接近。湿润体体积随灌水下限提高而提高，但体积增长速率减慢，超出计划湿润体以外水体体积也相应随灌水下限提高而提高。三个处理中计划湿润体体积线对应含水率分别为69%θFC、72%θFC，79%θFC，随灌水下限提高，计划湿润体内水分梯度降低，平均含水率提高。

图3 不同灌水下限滴灌结束土壤含水率等值线图

将计划湿润体之外湿润范围按照含水率分区间与计划湿润体体积作比，各区域所得比值与对应含水率变化率之积求和即可得到入渗到计划湿润体之外水量与滴灌灌水量之比，结果见表4。以50%θFC为灌水下限时潜在水量浪费最小，在旱区进行滴灌时，考虑作物耐旱能力前提条件下，应降低灌水下限，以便节水。

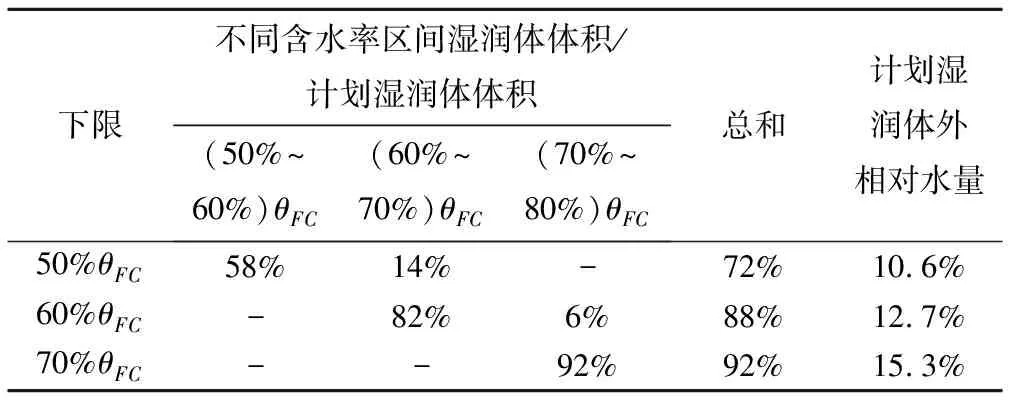
表4 不同下限处理水分入渗至计划湿润体外情况

注：计划湿润体外相对水量=计划湿润体外水量/灌水量。

3.2 不同灌水上限滴灌湿润体水分分布特征

滴灌结束时湿润体近似为半球体，各含水率等值面近似为半球面。作灌水下限为50%θFC、滴灌结束时不同含水率边界的湿润体体积随灌水上限变化曲线如图4。不同含水率边界湿润体体积随灌水上限提高均呈线性增长(R2值均达到0.97以上)，但斜率不同。由不同边界湿润体体积呈线性增长可推断,不同含水率区间湿润体积占整个湿润体体积比例不随灌水上限变化而变化。其他灌水下限的处理也得到了类似的结果。

图4 以50%θFC为下限，滴灌结束时不同含水率边界湿润体体积随灌水上限变化曲线

以土壤初始含水率起始边界，以增加10%θFC划分含水率区间(50%θFC至100%θFC划分5个区间)，不同灌水下限每一区间湿润土体体积占整个湿润体体积比例平均值如表5所示。对于同一灌水下限，以初始含水率为下边界的区间占比最高。灌水下限为60%θFC及70%θFC时，随区间含水率提高，占比逐渐降低；灌水下限为50%θFC时，占比有微小波动。纵向来看，含水区间(80%～90%)θFC的占比随灌水下限提高而提高；含水区间为(90%～100%)θFC的占比随灌水下限提高先下降后升高，但以70%θFC为灌水下限仍大于以50%θFC为灌水下限占比；含水率大于100%θFC体积占比随灌水下限升高变化不大，略有下降。

表5 不同处理滴灌结束时各含水率区间土体体积平均占比

3.3 不同灌水下限适宜灌水上限筛选

图5为不同灌水下限滴灌结束时湿润体体积与计划湿润体体积之比随灌水上限的变化情况。将湿润体体积与计划湿润体体积相等的点(即图中纵坐标为1的点)对应灌水上限作为相应灌水下限适宜灌水上限。

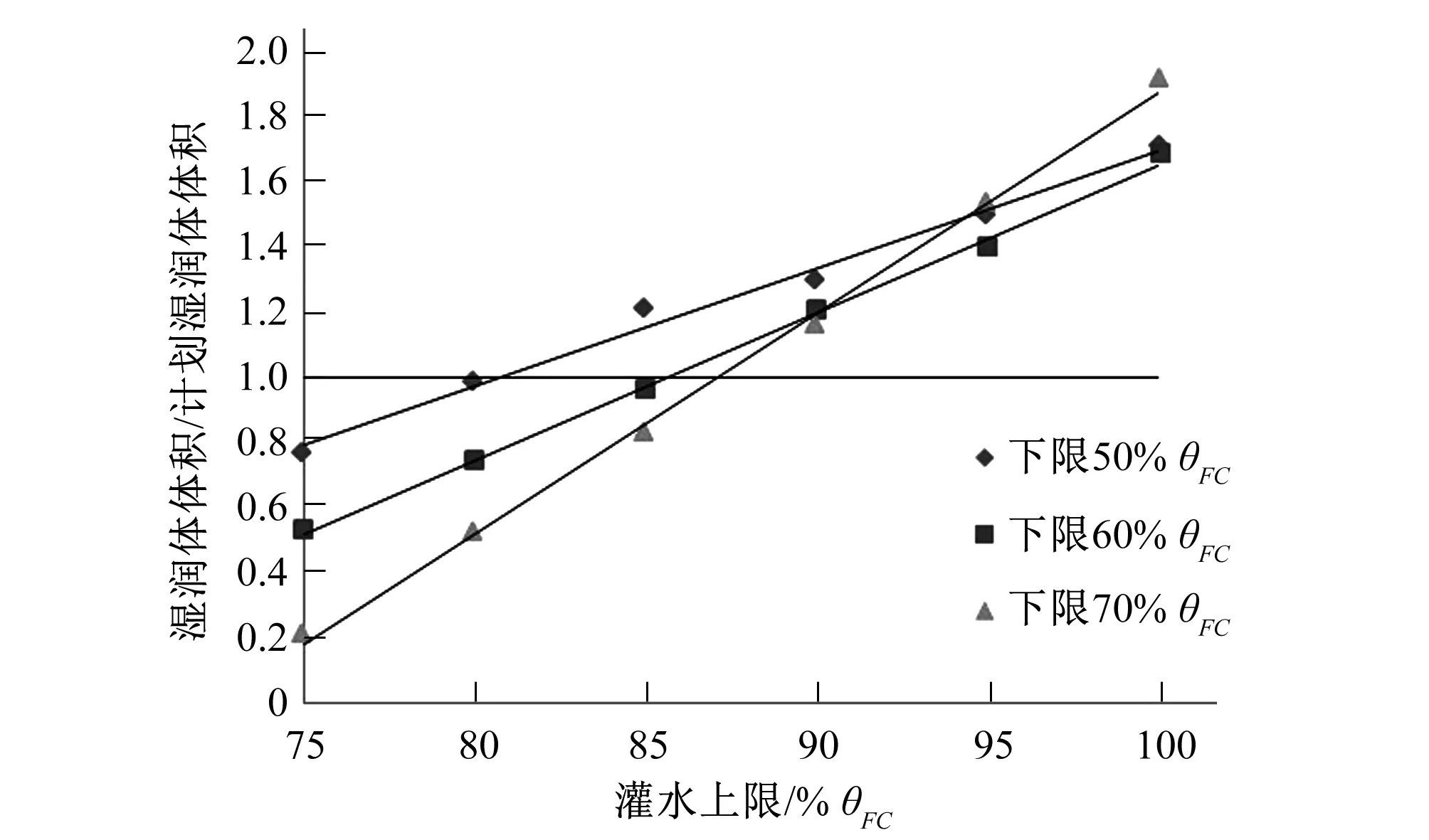
图5 不同灌水下限滴灌结束湿润体体积随灌水上限变化曲线

分析表明，以50%θFC为灌水下限时适宜灌水上限为81%θFC，以60%θFC为灌水下限时适宜灌水上限为85%θFC，以70%θFC为灌水下限时适宜灌水上限为86.5%θFC。

3.4 不同灌水下限适宜灌水上限湿润体内水分分布情况

以50%θFC，60%θFC，70%θFC作为灌水下限，选择3.3节中适宜灌水上限，再次利用HYDRUS进行模拟，滴灌结束时湿润体内水分分布情如图6所示。由图6可以看出，以适宜灌水上限滴灌结束时计划湿润体内水分梯度随灌水上限增大而减小，适宜灌水上限所得实际湿润体体积与计划湿润体体积3.9 万cm3基本相同，分别达到计划湿润体体积的96.9%、98.1%和93.0%，达到了精准控制湿润体体积的目的。

4 结论与讨论

滴灌是局部灌溉，基于作物根区精准控制计划湿润体是减少水量浪费、实现节水的关键。由于土壤水分运动的连续性，传统灌水上下限均会有水分运移到计划湿润体之外。土壤水分运移速率一方面取决于水势梯度，另一方面也取决于土壤非饱和导水率。在较高含水率条件下，沙壤土非饱和导水率快速增加，因此较高灌水下限滴灌湿润体超出计划湿润体比例增加，而较小的灌水下限有利于水分分布在计划湿润体体积内[12]。

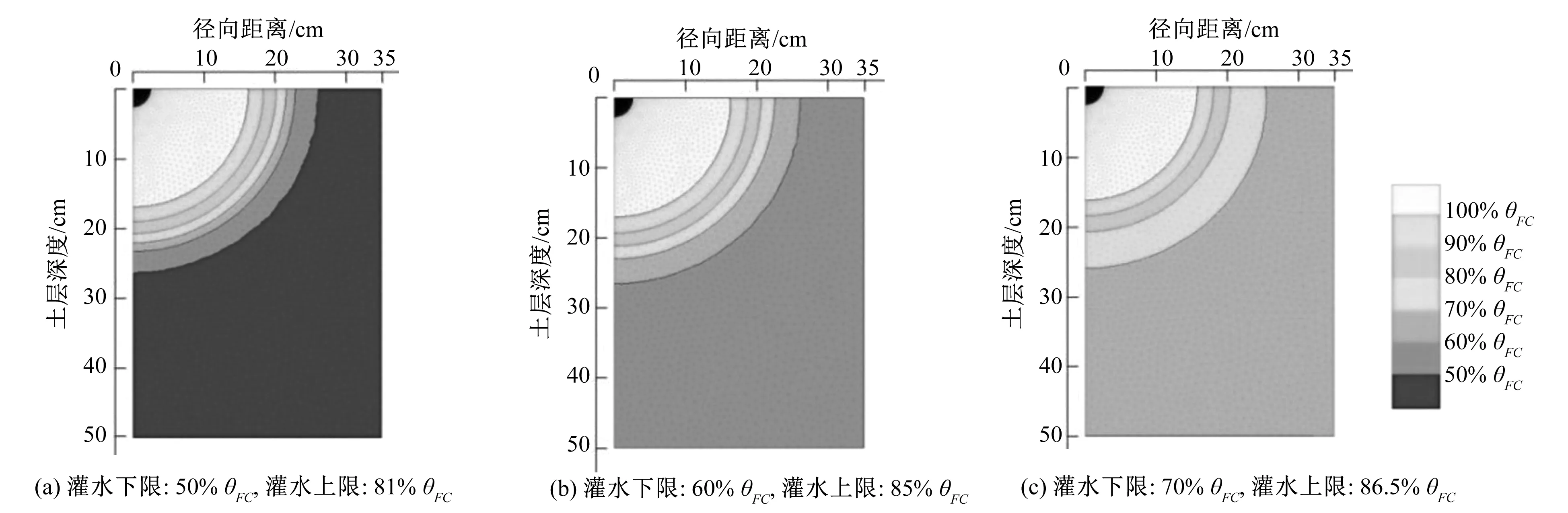
图6 适宜灌水上下限滴灌结束湿润体水分分布情况

灌水下限相同时，灌水上限决定着灌水定额。灌水定额过大，实际湿润范围增大，存在超出计划湿润体范围的可能。

研究发现，HYDRUS能精确模拟点源滴灌土壤水分入渗情况。模拟结果表明，以传统灌水上限100%θFC滴灌时，滴灌结束时均有灌溉水入渗到计划湿润体以外。灌水下限低，湿润体体积与计划湿润体体积接近，计划湿润体内水分梯度大，渗入计划湿润体之外的相对水量少。实际滴灌中，灌水上限一定时，适当降低灌水下限利于将水量更多控制在计划湿润体以内，减少潜在浪费。

同一灌水下限，滴灌结束时，湿润体内不同含水区间湿润体积占整个湿润体体积比例不变，占比随灌水上下限变化呈现一定规律。 对于本次试验土壤与计划湿润体，以50%θFC、60%θFC及70%θFC为灌水下限时适宜灌水上限分别为81%θFC、 85%θFC及 86.5%θFC。模拟表明对适宜灌水上限的筛选可以达到精准控制湿润体体积的目的。

本研究基于均质土壤滴灌入渗试验，湿润体特征以灌水结束时为准，没有考虑作物影响和土壤水分再分布过程。为提高结果的针对性，需要进一步在大田作物栽培条件下，考虑作物生长过程进行研究。