基于猫群思想的混合人工蜂群算法

赵玉霞，徐晓钟，黄 维，马 燕

(上海师范大学 信息与机电工程学院，上海 200234)

0 引 言

人工蜂群算法[1](artificial bee colony，ABC)是受蜂群采蜜过程启发的一种群智能算法，具有控制参数少、搜索能力强等优点[2]，已被用于连续空间优化[3]、数据挖掘[4]和神经网络优化[5]等多个方面。但ABC算法仍存在易“早熟”收敛和进化后期搜索能力较差的缺点，大量学者对此提出了多种改进方法，包括食物源初始化改进、观察蜂选择策略改进、解更新策略改进、与其他算法结合等等。

在食物源初始化改进方面，罗钧等[6]提出应用混沌序列初始化解，通过混沌的随机性、遍历性，提高解的多样性和搜索的遍历性。在观察蜂选择策略的改进方面，Bao等[7]提出三种新的选择机制：裂变选择、排序选择和竞标赛选择，并证明了新选择机制的有效性。在解更新策略的改进方面，Zhu等[8]在粒子群算法的启发下，提出基于最优解引导的解更新策略，提高了算法开采能力。Kiran等[9]在解更新策略中引入方向信息，降低了更新方向的盲目性，提高了算法速度。郝继升等[10]引入受差分进化算法启发的搜索方程，提高算法的搜索能力。在与其他算法结合方面，Ozturk等[11]将遗传算法与人工蜂群算法相结合，利用交叉和交换机制对食物源更新公式进行改进，使其跳出局部最优解。

以上改进从不同方面提升了算法优化能力，但是在提高算法收敛性的同时避免陷入局部最优方面仍旧有进一步的改进空间，因而文中提出基于猫群思想的混合人工蜂群算法，以通过新的搜索策略和搜索过程，以提高算法优化性能。

1 混合人工蜂群算法

1.1 基于随机新解引导的自适应搜索策略

基本人工蜂群算法根据式1建立初始种群，在雇佣蜂和观察蜂阶段根据式2进行邻域搜索，在侦查蜂阶段丢弃经过limit次搜索后未进行更新的食物源，再根据式1得到新的食物源。

xi,j=xmin,j+rand×(xmax,j-xmin,j)

(1)

vi,j=xi,j+ri,j×(xi,j-xk,j)

(2)

其中，xmin,j,xmax,j分别为食物源第j(j∈{1,2,…,D})维分量的下限和上限，rand为(0,1)之间的随机数；k∈{1,2,…,SN}且k≠i，ri,j是[-1,1]之间的随机数。

通过对函数寻优发现，基本ABC算法存在易陷入局部极值、易早熟收敛的问题。胡珂等[12]提到，迭代后期食物源位置相似度高，导致位置更新速度变慢。文中认为，迭代后期，现有搜索方程中的邻居从当前种群中选取，虽然侦查蜂阶段会对枯竭的食物源进行初始化，但依然有很大概率会选中当前食物源的相似食物源，二者差异较小，导致搜索能力下降，不利于跳出局部最优，从而导致算法早熟收敛。

Gao等[13]提出取消搜索方程中当前食物源的作用，新解完全由种群中随机选择的解生成，能利用更多信息进行搜索。但由于依旧是从当前种群中选择，选中相似食物源的概率依旧很大。因此，基于上述分析与启发，文中提出采用重新初始化生成的新解引导搜索，由于新解与当前食物源的相似度最低，有利于增强算法搜索能力。

新的搜索方程如下：

vi,j=xi,j+ri,j×(xi,j-Vr,j)

(3)

其中，Vr,j为根据式1生成的随机新解Vr的第j维值，其他参数含义同式2。该式具有较强的探索能力和随机性，利于算法跳出局部最优解，适合即将枯竭的食物源，但不适合搜索势头良好的食物源，因此为了保持算法稳定，在上式中加入种群中相邻食物源的引导作用，同时在文献[14]的启发下，提出基于当前食物源搜索现状的自适应搜索策略，以平衡两方面的引导力度。新的搜索方程如下：

vi,j=xi,j+μ×ri,j×(xi,j-xk,j)+(1-μ)×φi,j×(xi,j-Vr,j)

(4)

其中，φi,j为[-1,1]之间的随机数；μ为调节相邻食物源引导力度与随机新解引导力度的平衡因子，自适应过程如下：

μ=1-trial(xi)/limit

(5)

其中，trial(xi)为食物源xi的连续开采失败次数；limit为算法参数，一定程度上代表trial(xi)能达到的最大值。当搜索到更优解时，trial(xi)被重置为0，此时应侧重于相邻食物源引导，以进行平稳搜索；随着对食物源的开采接近枯竭，trial(xi)值增大，此时应加大随机新解的引导力度，引导算法向更有利区域进行搜索，以跳出局部极值。另外，当侦查蜂阶段判定某食物源枯竭时，将对其进行重新初始化，对应trial(xi)被重置为0，虽然根据式4将侧重于在相邻食物源的引导下搜索新解，但由于当前食物源本身是初始化后的新解，因而两方面的引导相统一，此时式4满足算法搜索需求。

1.2 多次高斯搜索机制

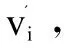
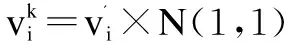
(6)

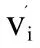
基于随机新解引导的自适应搜索策略的目的在于加大解的随机性，提高种群多样性，避免陷入局部最优，因此新解会携带较多的随机信息，但质量不一定比旧解更好。而基本ABC算法的贪婪选择策略更偏向于解质量的提高，因此搜索到的新解有很大的概率会被丢弃，则新的搜索策略难以发挥作用。因而引入多次高斯搜索机制，在新解被丢弃前，以新解为中心，进行多次高斯搜索，并保留搜索过程中得到的最优解，再与旧解进行贪婪选择，达到保证解的质量和跳出局部最优之间的平衡。

综上，改进雇佣蜂阶段流程如图1所示。

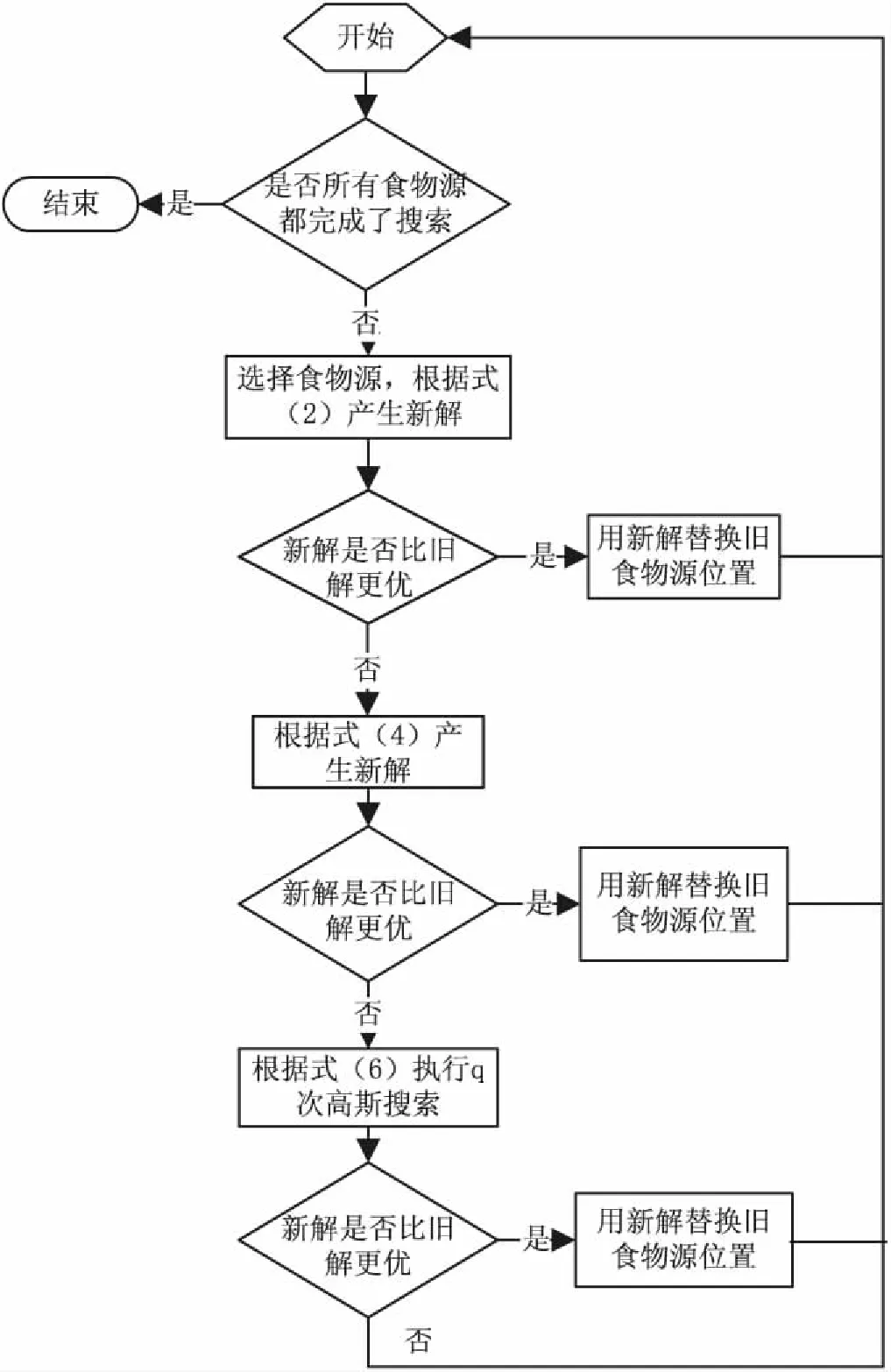
图1 改进雇佣蜂阶段流程

1.3 基于猫群思想的搜索过程

由于ABC算法原始搜索策略随机选择邻居食物源和步长进行搜索，具有较好的探索能力。虽然算法早期需要较强的探索能力来搜索尽可能多的最优解，但若能同时配合较强的开采能力，则能有效加快算法收敛速度，后期收敛精度也更高。因此众多学者从提高开采能力的角度提出了不同的搜索策略。

文中从混合算法角度出发，提出基于猫群思想的搜索过程，一方面蜂群算法与猫群算法的混合研究较少，另一方面，对猫群算法研究后发现，通过有效结合，其局部搜索方式和全局搜索方式能更有针对性地提高ABC算法的局部开采能力和全局搜索能力，进而提高算法性能。

1.3.1 猫群算法分析

猫群算法[15](cat swarm optimization，CSO)将猫的行为模式分为搜寻模式和跟踪模式。搜寻模式下，通过对个体进行多次扰动，完成每个个体向局部最优靠近的过程，即搜寻模式主要承担局部搜索工作。跟踪模式下，猫以一定速度对目标猎物进行跟踪，通过与群体最优位置进行比较来更新个体位置。跟踪模式本质上是向全局最优靠近的过程，这种“社会性”利于算法进行全局搜索。

1.3.2 跟踪模式优化

跟踪模式类似于粒子群算法，利用全局最优位置不断更新猫的当前位置，使得当前解不断向最优解逼近，最终达到全局最优解。该模式下猫的速度与位置更新公式如下：

vi(t+1)=vi(t)+c1×rand×(x*-xi(t))

(7)

xi(t+1)=xi(t)+vi(t+1)

(8)

其中，x*表示猫群目前最好的位置；c1为加速系数；rand为[0,1]区间内的随机数；vi(t)和vi(t+1)分别表示第t次和第t+1次迭代时猫的速度；xi(t)和xi(t+1)分别表示第t次和第t+1次迭代时猫的位置。

该模式采用“速度-位移”模型，效果较好，但速度参数只应用在跟踪模式下，在搜寻模式中未应用，利用率不高；考虑到要和采用“位移”模型的ABC算法结合，因此从简化算法和便于算法结合的角度出发，提出去掉速度参数，采用位置跟踪方式，根据下式进行解更新：

xi(t+1)=xi(t)+φi×(x*-xi(t))

(9)

其中，φi在[0,1]区间随机取值，其他参数含义同式7。可知，该式同样实现了跟踪全局最优解的功能，且更加简洁。

1.3.3 基于猫群思想的搜索过程

由上文可知，猫群算法的搜寻模式和跟踪模式分别具有较强的局部搜索能力和全局搜索能力，而ABC算法具有易“早熟”收敛和后期开采能力较差的缺陷，因而提出将猫群思想引入到基本ABC算法中，在观察蜂阶段之后，加入基于猫群思想的搜索过程，同时采用顺序模式分配方式，实现算法结合。

顺序模式分配是相对于猫群算法随机分配方式而言的。随机分配方式是指在确定执行跟踪模式个体的数量后，随机选择对应数量的个体执行跟踪模式，而顺序模式分配方式是先对个体依据适应度值进行升序排序，再顺序依次分配模式的方式。具体地，根据适应度值和MR参数，将食物源分为较优食物源和较差食物源，对较优食物源执行搜寻模式，对较差食物源执行跟踪模式。

通过对两种模式的分析，可知顺序模式分配的好处在于搜寻模式能对优质食物源进行充分精细的局部搜索，有针对性地提高算法的局部搜索能力；而跟踪模式能引导较差食物源向全局最优靠近，减少对该食物源的无效搜索次数，提升算法效率；从而通过两种模式的配合，提高算法整体搜索能力。

1.4 混合人工蜂群算法

综上，在基本ABC算法的雇佣蜂阶段引入基于随机新解引导的自适应搜索策略作为原始搜索策略的补充，同时结合多次高斯搜索机制，完成雇佣蜂阶段寻优任务；在观察蜂阶段之后，引入基于猫群思想的搜索过程，采用顺序模式分配方式，对较优解执行搜寻模式，对较差解执行优化后的跟踪模式；在搜索过程结束后进入侦查蜂阶段，完成接下来的寻优任务，得到混合人工蜂群算法(hybrid ABC，HABC)。算法流程如图2所示。

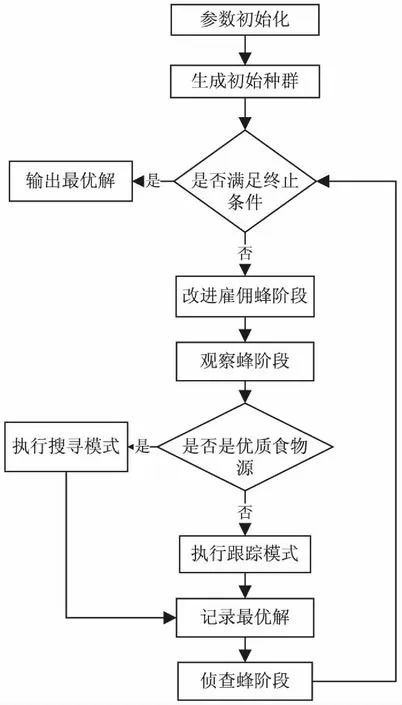
图2 混合人工蜂群算法流程

2 实验验证

2.1 参数设置与测试函数

为验证文中改进策略的有效性，将仅引入基于随机新解引导的自适应搜索策略和多次高斯搜索机制的改进人工蜂群算法命名为MABC，将仅采用优化跟踪模式的改进猫群算法命名为MCSO，HABC算法则是在MABC的基础上引入基于猫群思想的搜索过程，该搜索过程采用优化后的跟踪模式。选取6个测试函数对算法性能进行验证，并将结果分别与基本人工蜂群算法ABC和基本猫群算法CSO进行比较。

测试函数见表1。其中Sphere、Schewefel 2.22为单模函数，单模函数检验算法局部搜索能力，测试算法收敛速度和寻优精度；Griewank、Ackley、Rastrigin、Schaffer为复杂多模函数，多模函数检验算法综合能力，测试算法搜索全局最优解、摆脱局部最优解的能力。

算法参数设置：种群规模N=60，个体维数D=30和D=60,最大评价次数分别为2 000和4 000。对于CSO算法,SMP=5,SRD=0.2,CDC=0.8,SPC=0,MR=0.02,c1=2.05。MCSO算法参数同上。对于MABC算法，q=10,其他参数同上。对于HABC算法，MR=0.5,其他参数同上。算法独立运行30次，并记录多次运行结束后的最优值、平均值、最差值和标准差，展示在表2中。各算法的收敛曲线对比如图3所示，为了便于对比，只展示了部分迭代次数下的收敛曲线。

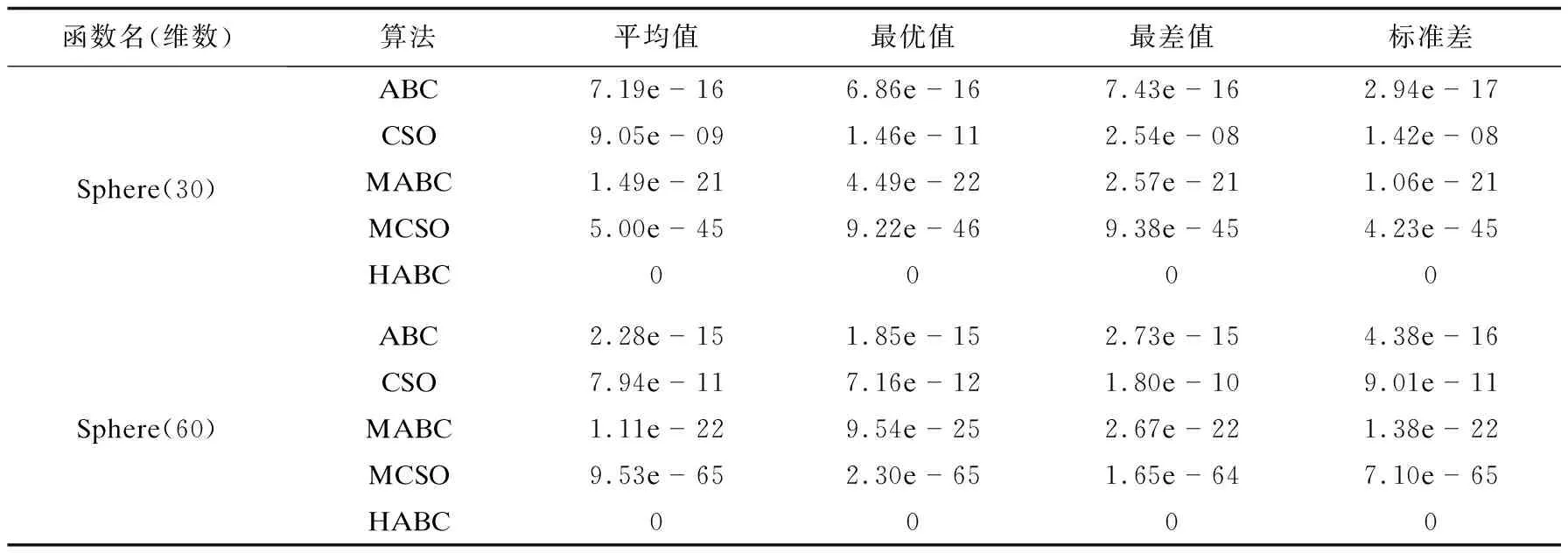
表2 各算法收敛精度对比

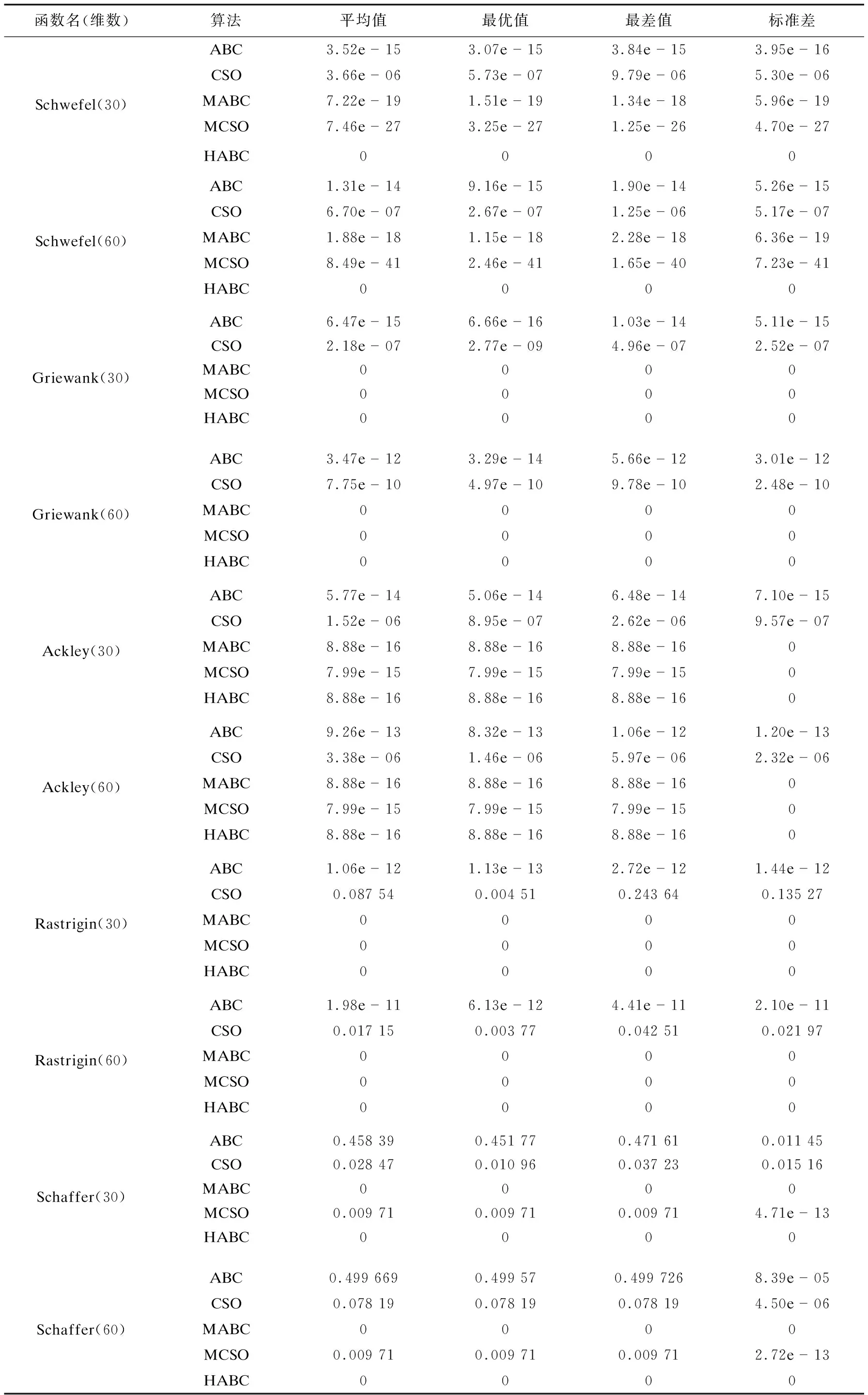
续表2

2.2 结果分析

由表2可知，与ABC算法相比，MABC算法收敛精度更高；与CSO算法相比，MCSO算法收敛精度更高；而HABC算法收敛精度则优于MABC和MCSO算法，表明文中提出的改进策略和混合人工蜂群算法的有效性。具体的，对于单模函数，MABC算法收敛精度得到一定程度提高，对于多模复杂函数，MABC算法优势突出，能收敛到理论最优解，表明基于随机新解引导的搜索策略和多次高斯搜索机制相结合，能有效增加种群多样性、缓解算法易陷入局部极值的问题。MCSO算法在单模和多模函数上收敛精度都得到不同程度的提升，表明优化后的跟踪模式不仅简化了算法，而且具有更强的搜索能力。HABC算法在MABC算法的基础上，增加了基于猫群思想的搜索过程，由表2可知，对于单模函数，HABC算法能唯一收敛到理论最优解，表明了基于猫群思想的搜索过程能有效提高算法局部搜索能力；对于多模函数，HABC算法与MABC表现一致，除了Ackley函数，均能收敛到理论最优解，表明HABC算法具有MABC算法的优点，对于多模复杂函数具有较好的优化性能。而在Ackley函数上，应用优化策略后收敛精度也得到了一定程度的提升。

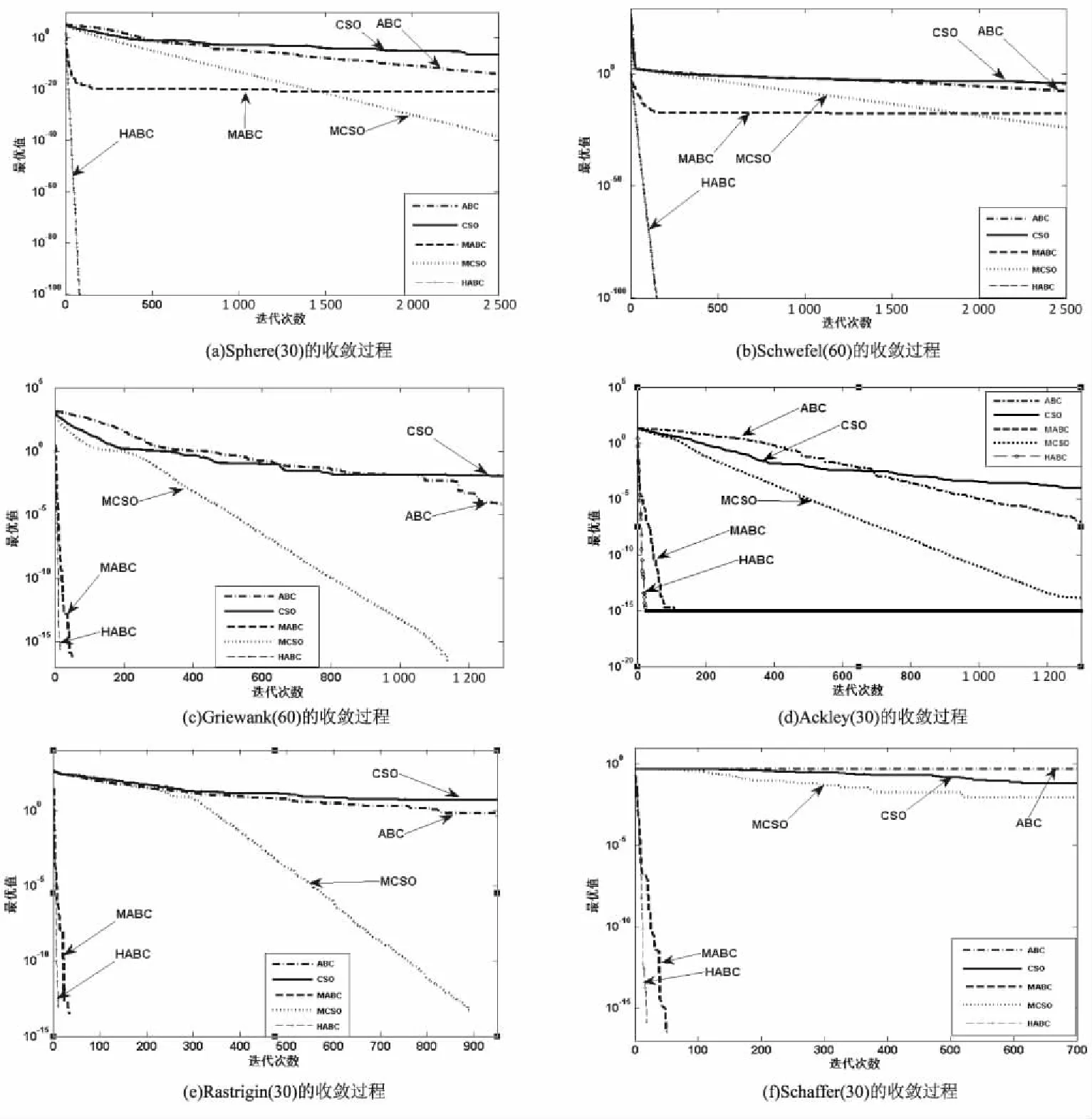
图3 各算法收敛过程对比

通过图3对各算法收敛速度进行分析可知，MCSO算法相比CSO算法，达到最后收敛精度所需的迭代次数有了不同程度的下降；MABC算法与ABC算法相比，在多模函数上，所需迭代次数显著下降；HABC算法则在单模函数和多模函数上，都能在最少的迭代次数内达到最优收敛精度。

可见，优化后的跟踪模式在简化算法的同时，一定程度上加快了算法收敛；基于随机新解引导的搜索策略与多次高斯搜索机制的结合，能有效应对多模函数易陷入局部极值的问题，进而提升算法收敛速度；基于猫群思想的搜索过程则通过加强算法的局部搜索能力和全局搜索能力，显著提高了对单模函数的收敛速度。

3 结束语

针对基本人工蜂群算法存在的缺陷，提出新的混合人工蜂群算法。具体地，在雇佣蜂阶段引入基于随机新解引导的搜索策略和多次高斯搜索机制；在观察蜂阶段后，引入基于猫群思想的搜索过程；对原始跟踪模式进行优化。

通过标准函数的验证表明，基于随机新解引导的搜索策略与多次高斯搜索机制的结合能有效应对多模函数易陷入局部极值的问题，有效提升算法收敛速度和收敛精度；基于猫群思想的搜索过程能有效提高算法局部搜索能力和全局搜索能力，收敛精度得到大幅提升；优化后的跟踪模式在简化算法的同时一定程度上提高了算法收敛速度；综合以上优化策略的混合人工蜂群算法的优化性能最优。