基于被动分簇的时间同步容错技术研究

王 盼，刘广钟

(上海海事大学 信息工程学院，上海 201306)

0 引 言

近年来，随着水声传感器网络技术的发展，水声传感器网络的应用越来越广泛，水声传感器网络凭借其分布性、低成本等优点被广泛应用于海洋监测、污染监控、资源开采、海难搜救等众多领域[1]。但是，由于水声传感器网络中受自身计算、通信、存储等能力的硬件限制和水声通道高延迟、低带宽、多路径等特性[2]，水声传感器网络时间同步过程中容易受到攻击，因此对水声传感器网络时间同步过程中容错技术的研究是必不可少的。

因为水声传感器网络的环境恶劣，对每一节点都进行同等的要求是不现实的。出于节能和高效的考虑，多采用分簇的层次网络拓扑结构[3]，重点是每一个节点时间同步的调整有一个上限。在无线传感器网络中，相比于叶子节点，簇头节点的计算、通信、存储等能力是较高的[4]。所以该方案中簇间节点可以直接通过广播的方式与其他节点进行交流，在每一次的时间同步中，只有一个节点作为同步器来发送同步信息，这样就避免了信息碰撞的问题。在簇头节点自身的时钟调整也有一个上限，从而提高节点的利用率。

1 容错时钟同步模型

时钟同步模型[5-8]如下所示，文中出现的符号及其含义如表1所示。

表1 符号及其含义

首先对绝对时间和时钟时间做了比较。绝对时间是一种精确的时间，时钟时间是一种可以在传感器节点的时钟上看到的时间。用小写字母表示和绝对时间有关的变量和常量，用大写字母表示和时钟时间有关的变量和常量。

(1)

由公式λ=ρ(2+ρ)(1+ρ)可以得到任意两个正常节点间的漂移率是有界限的，且漂移率会少于2ρ。传感器节点中通常包含廉价的晶体振荡器，时钟漂移率在几十微秒左右。如果一个节点可以正确执行给定的时钟同步算法就称为正常节点。假设时钟同步是循环执行的，每一轮包括R个时间单位。对于两个正常节点，在时间段[begf,endf]内存在最大时钟漂移率δ，则有：

δ=2ρ(endf+1-endf)

(2)

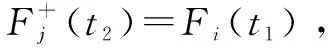
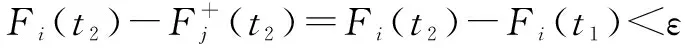
(3)

其中，ε=(1+ρ)φ是时钟读数错误的上限，包括最大的传输时延和在时延中的时钟漂移率。

假设在开始时间t0，正常节点i和j之间的时钟差异小于δ0，即有：

|Fi(t0)-Fj(t0)|<δ0

(3) 在塔-线体系导地线和杆塔同时发生共振时,同阶共振的两个相邻单塔会出现共振方向相同和相反两种振型形式.在同阶情况下,与单塔模态频率相比,塔-线体系中的单塔共振频率值要小,而且垂直向要比水平向更加明显.

(4)

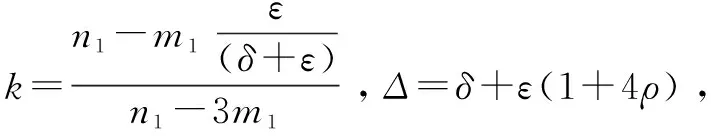
(1)在节点数量为n1的簇中，对于任意两个节点i和j,任意时刻的绝对时间对应的时钟时间有一个上限，对于所有的t∈[begf,begf+1]，存在：

|Fi(t)-Fj(t)|≤(2km1+1)Δ+m1δ+2ρε

(2)如果一个节点在t时刻对它自身的时钟进行调整，则存在一个上限，即|F+(t)-F(t)|≤kΔ。

2 簇间容错时钟同步方案

容错时钟同步主要分为两个过程：拓扑建立和时间同步。

2.1 拓扑建立

拓扑建立的方式有很多种，例如基于簇树混合的分簇方法[9]、自组织分簇休眠方法[10]等等。基于簇树混合的分簇方法首先进行分簇，确定簇首节点和簇成员节点，然后再以基站节点为根，以树型结构把所有的簇首节点连接起来。此方法考虑能耗均衡的问题，需要周期性地建立网络拓扑结构，通信能耗较高。自组织分簇休眠方法是节点自行进行分簇，根据节点是否被激活判断是否加入簇中。此方法虽然将节点是否被激活考虑进来，但是准确率不高，导致节点的闲置，造成不必要的浪费。文中则采用基于被动分簇的分簇方式进行分簇，由于被动分簇是在其他算法进行泛洪的时候进行，使得通信能耗减少，提高了节点的利用率。

在被动式分簇[11-14]方案建立簇的过程中，网络中的节点可能处于6种不同的状态，分别是初始化、预备簇首、簇首、一般簇成员、预备网关和网关。基于被动分簇的层次型网络结构如图1所示。

2.2 容错时钟同步算法

这部分主要介绍簇间的容错时钟同步，被网关节点连接的簇间节点彼此之间可以通过广播的形式进行通信，而且簇间节点之间时钟的调整有一个上限。假设每一个簇中的节点轮流担任同步器，通过广播的方式与其他节点进行信息交流，此时的同步器同时担任簇首节点。假设f为同步的轮数，每一轮包括R个时间单位，同步器每变换一次，f的值就增加1，并与其他簇的簇首节点进行信息交换。

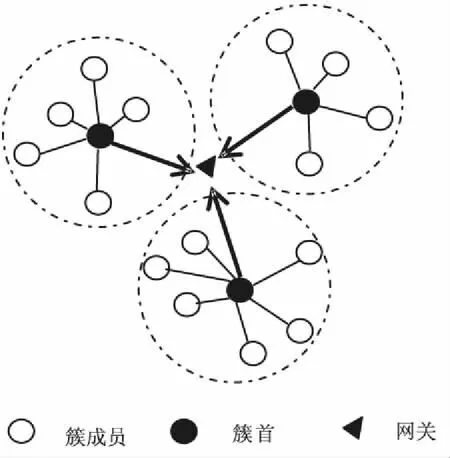
图1 基于被动分簇的层次型网络

假设对于一个网关节点连接的任意两个簇首节点l1和l2，在进行时钟同步时,任意时刻的绝对时间对应的时钟时间满足被动分簇下时间同步容错算法(fault-tolerant clock synchronization based on passive clustering，SP)：

|Fl1(t)-Fl2(t)|≤(2km+1)Δ+mδ+2ρε+kΔ

令：x=(2km+1)Δ+mδ+2ρε+kΔ

证明：使用反证法。假设对于任意的簇首节点l1和l2，当t∈[begf,begf+1]时，有|Fl1(t)-Fl2(t)|>(2km+1)Δ+mδ+2ρε+kΔ。根据式1和式2，正常同步器之间最大的时钟差是δ+ε(1+6ρ)。根据条件1，一个恶意节点在簇间可以增大的最大时钟差最多为2kΔ+δ，所以只有当恶意节点的数量最少为m1+1时，最大时钟差距才大于m1(2kΔ+δ)+δ+(1+6ρ)ε。因为恶意节点的数量最大为m1，只有当一个恶意节点作为两次同步器的时候以上假设才会成立。

所以，有(n1-m1)(k-1)Δ≤(2km1+1)Δ+m1δ+2ρε，显然之前的假设不成立，得到：

|Fl1(t)-Fl2(t)|≤(2km+1)Δ+mδ+2ρε+kΔ

具体算法描述如下：

(1)当节点在同步过程中自身时钟为T时接收到同步消息，如果此时Tf×R+x，节点就要把信息丢弃。

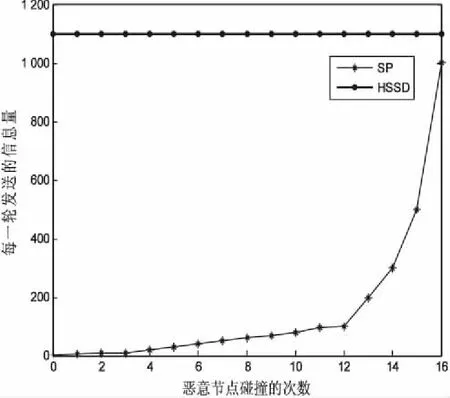
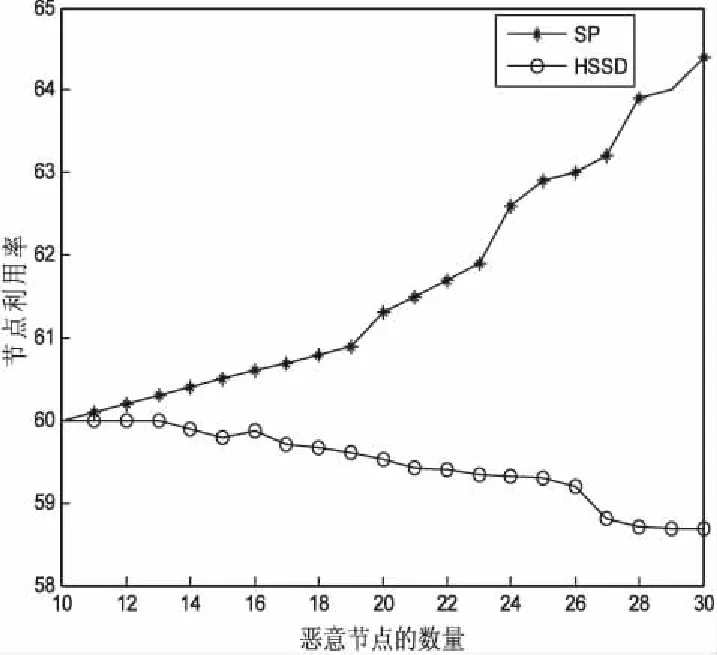
(2)当节点在同步过程中自身时钟为T时接收到同步消息，如果T∈[f×R-x,f×R+x]，就计算时钟差Θ=f×R-T,并且做以下调整：如果|Θ|

(3)当节点没有接收到同步消息，则改变同步器进行下一轮同步。

3 仿真实验

文中采用NS-2网络平台[15-18]下的水声传感网络模拟器作为容错算法的仿真工具。仿真过程重点对比HSSD[19]时间同步协议与文中提出的SR容错算法的节点利用率。

仿真实验中重要讨论容错算法对节点利用率的影响。采用的部分参数如下：每2分钟被同步一次，时钟漂移率ρ=106，最大时钟读数误差是0.000 1 s。恶意节点的数量在仿真中给出，仿真环境为水声环境。

为了弄清楚在现实中最大时钟差是如何达到的，做了一系列模拟实验。用100 000个不同的节点进行测试，取n=24，图2显示了理论和现实的最大时钟差的差异。实验结果显示，无论是理论值还是测试值，最大时钟差都会随恶意节点的增多而增大,而且最大时钟差的理论值总是比实际测量值要大，即文中提出的最大时钟差理论上是不会达到的。

图2 最大时钟差对比

图3 算法结果对比

图3是HSSD算法和SP算法的对比图。与SP算法不同的是，HSSD算法在进行时间同步时采用单播的形式进行信息交流，在恶意节点存在的情况下，HSSD算法每一轮的信息量是不变的，这就为时间同步容错技术带来阻碍。而SP算法时间同步采用广播的形式，虽然信息量会随着恶意节点碰撞次数的增多而增多，但这也为容错技术的实施奠定了基础，使得在最大时钟差范围之内的恶意节点重新恢复正常节点的身份，提高了整个网络节点的利用率。

图4给出了SP算法和HSSD算法在恶意节点存在时的节点利用率。根据实验可以得出，当只进行时间同步而不容错的情况下，节点利用率呈下降趋势；而使用SP容错算法可以使一部分恶意节点恢复正常节点身份，大约可以让4%左右的节点被重新利用，大大提高了节点的利用率。

图4 利用率对比

4 结束语

集群式时间同步容错技术考虑的是簇内节点之间的时间同步，文中在集群式时间同步容错的基础上提出了基于被动分簇的时间同容错技术。该方案由于使用被动分簇，节省了开销。容错算法针对的是簇间时间同步，相对于只考虑簇内时间同步容错技术，该方案的容错范围相对来说比较广。仿真结果表明，在恶意节点存在的情况下，时间同步过程中使用SP算法可以提高节点的利用率。

未来的工作应着力于恶意节点自身的研究，不断优化算法，在提高节点利用率的基础上，改进节点的能耗的使用，延长节点的使用寿命。