一种基于解析表达的SAR海面信号多普勒中心全谱模型
牛树华,马 丹,王小青,黄 默,周智勇
(1.海军装备部,北京 100040;2.上海微波设备研究所,上海 201802;3.中国科学院微电子研究所,北京 100029)
0 引 言
合成孔径雷达(SAR)是当今海洋遥感的重要手段,从SAR海洋图像中可以获取海面风、浪、流、内波等很多信息。其中从SAR海洋图像信息中提取流场信息是目前SAR海洋遥感中的热点问题。目前从SAR海洋图像中提取海面流场信息主要基于2个机理。
第1个机理是海面流场的辐聚辐散效应会导致海面后向散射强度的调制,Alpers and Hennings(1984年)最早建立了海面流场调制效应的SAR成像模型[1],但是该模型只考虑了Bragg波的作用,大大低估了L波段以上频段的海面流场调制效应,此后Holliday、Lyzenga、Thompson、Romeiser等人采用复合表面模型等方法对海面散射及其波流调制效应模型做了一些改进[2-5],这些模型考虑了中尺度波的调制效应,使得仿真结果与试验结果更为接近,但在一些情况,尤其是高波段情况下还是低估了流场对散射调制。Kudryavtsev 和 Johannessen等人发展了一个半经验的雷达成像模型(RIM),该模型考虑了波浪破碎对海面散射和流场调制效应的影响,使得高波段的仿真结果与实测数据得到了较好的吻合[6-7]。
第2个机理是海面流场会导致SAR方位向信号多普勒中心的偏移。但是SAR海面信号的多普勒偏移机理非常复杂,除了海面流场在雷达视向投影有贡献外,波浪的轨道速度和调制效应都会对多普勒偏移有贡献。只有建立准确的波浪对多普勒中心偏移贡献量的模型,才能从SAR信号多普勒中心中剔除表面波浪的贡献,从而提取出海面流场的贡献量。Romeiser and Thompson[8]采用复合表面模型的仿真方法分析了海面多普勒中心与波浪谱的关系,在该模型中将海面假设为由许多Bragg散射体构成,大尺度波通过调制效应改变Bragg散射体的运动和散射强度,最终的多普勒中心是所有散射体多普勒中心散射加权的结果。但在该文中使用的是线性调制传递函数(MTF)。Chapron等人在此基础上采用Kudryavtsev等人建立的非线性调制传递函数分析了海面多普勒中心与波浪谱的关系,并用EnviSAT的高级合成孔径雷达(ASAR)数据证实了从SAR多普勒中心信息提取流场信息的能力。J. A. Johannessen和B. Chapron在此基础上又考虑了镜面反射对普勒中心的贡献。
基于这2个机理,Johannessen等人提出了DopRIM的海面流场反演方法,在这个方法中如何从多普勒中心剔除表面波浪的贡献是一个非常关键的步骤。以往对于多普勒中心与表面波浪谱的关系主要是基于双尺度模型或者复合表面模型进行研究。但是双尺度模型是一种简化理论,并不是一个很严谨的理论,其分割尺度也往往取决于经验猜测。而实际上各种谱分量对多普勒中心的贡献是非常复杂的,各种波谱分量除了自身对散射产生贡献外,对海面轨道速度也都有贡献,这些贡献是相互耦合的,并不能简单地进行尺度分割。
为了使得海面波浪的多普勒中心模型更严格和精确,本文建立了一种基于解析表达的全谱模型的SAR多普勒中心与海浪谱的关系模型,该模型涵盖了所有谱分量的散射和运动的贡献。该模型比双尺度模型在理论上更严谨和精确。理论分析表明如果只考虑|K|≪Kb和|K|≈Kb两部分频谱,则全谱模型可以近似为双尺度模型。但是仿真表明双尺度模型忽略的中尺度波贡献可以达到30%~50%。所以双尺度模型忽略中尺度波的贡献会导致海面流场估计中较大的误差。仿真也表明采用全谱模型和双尺度模型计算出的多普勒速度存在较大的差距。对于L波段低视角情况下,这个速度差异可以达到1 m/s,在通常情况下这个速度差异可以达到0.2~0.4 m/s,这个速度误差对于高精度海流估计来说是不可忽略的。
1 理论建模
海面SAR回波信号在进行距离向压缩处理后,某距离门内SAR回波可以表示为:
(1)
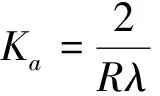
对式(1)进行傅里叶变换可以得到方位向信号的频域表达式:
S(ω)= ∬p(x,t)exp[-jπKa(x-vt)2]
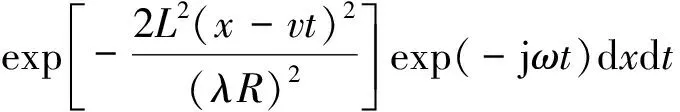
(2)
则多普勒频域的功率谱为:
T(ω)= 〈S(ω)S*(ω)〉=

(3)
考虑到海面散射空间相关性很小,远小于分辨单元,因此:
〈p(x1,t1)p*(x2,t2)〉≈ρ(0,t2-t1)δ(x1-x2)
(4)
式中:ρ(x,t)=〈p(x1,t1)p*(x1+x,t1+t)〉,为海面散射系数的自相关函数。
令x=x1-x2,X=(x1+x2)/2,t=t1-t2,T=(t1+t2)/2,则:
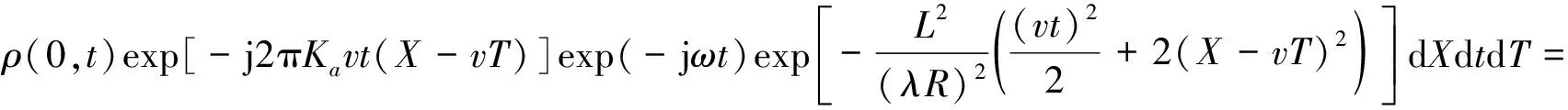
(5)
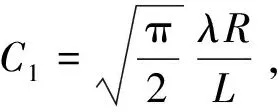
多普勒中心的定义为:
(6)
令:
(7)
根据傅里叶变换的性质,有:
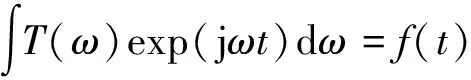
(8)
则:
(9)
(10)
从式(7)可以得出:
(11)
所以:
(12)
式(12)表明SAR海面信号的多普勒中心可以等效为海面电磁散射系数自相关函数的多普勒中心。
根据积分电磁(IEM)散射模型,如果只考虑单次散射(在入射角小于60°情况下海面散射主要是单次散射),则海面的散射可以表示为:
(13)
式中:Γpq为一个与极化和入射角有关的比例系数;p、q分别为发射和接收的极化方向;kh为电磁波波束矢量在x方向的投影(x方向与电波入射方向在水平面投影平行)。
Γpq=fpq+[Fpq(-kh,0)+Fpq(kh,0)]/4
(14)
式中:fpq为基尔霍夫散射系数;Fpq为剩余项系数。
在这里我们另外再考虑水平位移以及SAR的二维点扩展函数,则式(12)变为:
E(t)=Γpq∬exp[j2kzz(x,y,t)]·
exp(-j2khd(x,y,t))exp(-j2khx)·
(15)
式中:kz为电磁波数在垂向的分量;kh为电磁波数在水平方向的分量;z为波高;d为水平位移。
根据流体波动力学理论,深水海面的垂向位移和水平位移振幅相同,但相位相差90°,垂向位移和水平位移可以表示为:
z(x,y,t)=∬a(Kx,Ky)exp[j(Kxx+Kyy-ω(Kx,Ky)t)]dKxdKy+c.c.
(16)
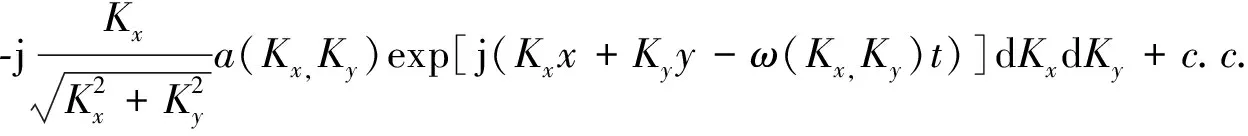
(17)

令:
(18)
则海面散射时间相关系数可以表示为:
ρ(0,t)= 〈E(t1)E*(t1+t)〉=|τpq|2∬∬〈exp[jg(x1,y1,t1)-jg(x2,y2,t1+t)]〉
(19)
如果海面波高满足高斯随机分布,则:
〈exp[jg(x1,y1,t1)-jg(x2,y2,t1+t)]〉=exp[-φ(0,0,0)+φ(x2-x1,y2-y1,t2-t1)]
(20)
式中:φ(x,y,t)为g(x,y,t)的自相关函数,并有:
φ(x,y,t)= 〈g(x′,y′,t′)g*(x′+x,y′+y,t′+t)〉=
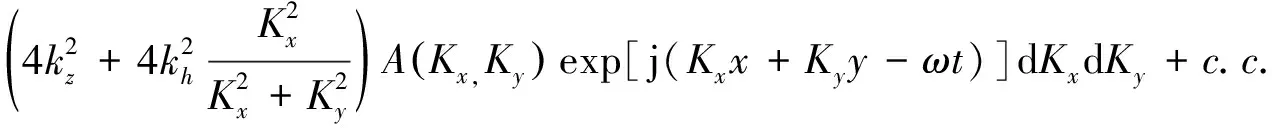
(21)
式中:A(Kx,Ky)=〈a(Kx,Ky)a*(Kx,Ky)〉,为波浪谱。
令x=x1-x2,X=(x1+x2)/2,y=y1-y2,Y=(y1+y2)/2,t=t1-t2,且:
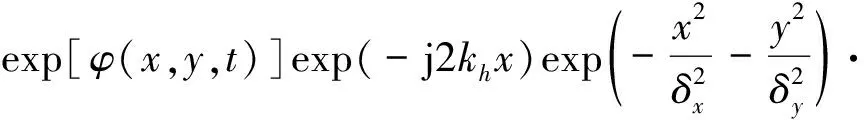

(22)
这样多普勒中心可以表示为:
(23)
令:
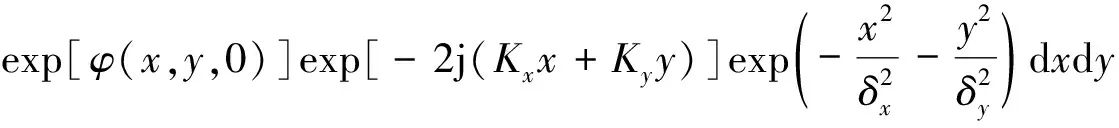
(24)
σ(Kx,Ky)就代表了当电磁入射波数为[kz,Kx,Ky]时的海面散射强度。所以:
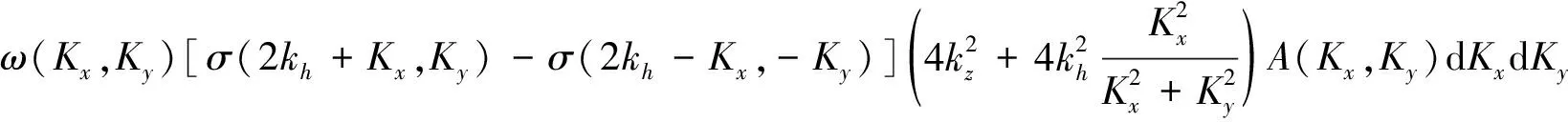
(25)
当φ(0,0,0)≪1,并且考虑到δx≫λ,δy≫λ,经过一些运算和化简可得:
(26)
A(2kh,0),A(-2kh,0)分别代表2个方向传播的Bragg波谱。由于Bragg波的振动频率ω=cb·2kh=4πcbcosθ/λ,即为Bragg波相速度对应的雷达多普勒频率。
式(26)的含义可以理解为:在海面粗糙度足够小的情况下,多普勒中心是正向和反向传播的Bragg波相速度对应的多普勒频率与其波谱强度的加权和。这种情况下与双尺度模型中Bragg波相速度的贡献是一致的。
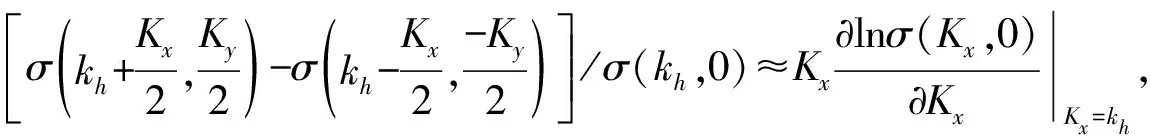
(27)
在双尺度模型中,大尺度波的散射调制和轨道速度的耦合项为:
(28)

在前面的全谱模型中我们没有考虑海面的松弛率,如果考虑松弛率,并且使得全谱模型简化后能与双尺度模型近似相等,则多普勒中心的全谱模型应重写为:
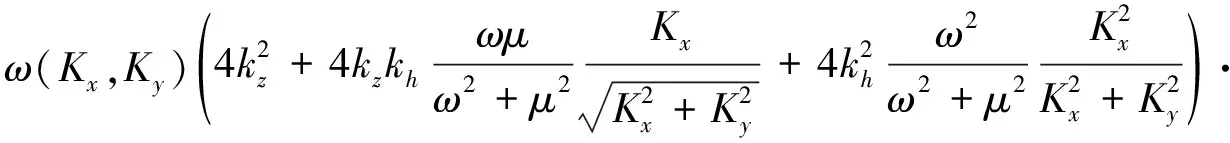
[σ′(kh+Kx/2,Ky/2)-σ′(kh-Kx/2,-Ky/2)]A(Kx,Ky)dKxdKy
(29)
其中:
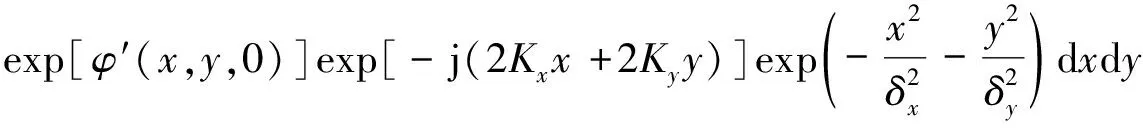
(30)
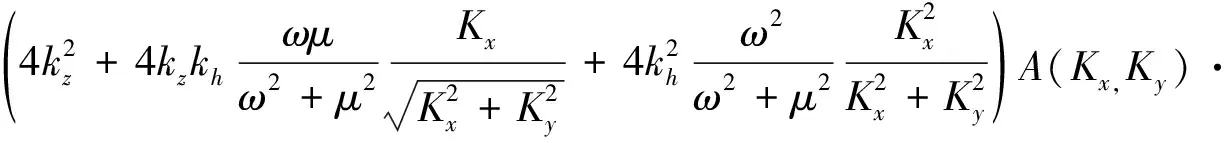
exp[j(Kxx+Kyy-ωt)]dKxdKy+c.c.
(31)
文献[9]将大尺度散射对多普勒的贡献解释为大尺度散射和“镜面散射点”漂流速度的加权和,但是从式(27)可以看出,这个说法也许是不对的,大尺度的贡献只是式(27)中的一部分,如果将散射分解为大尺度散射和小尺度散射之和:
(32)
式中:k1为大尺度和小尺度的分割波数,则大尺度散射的贡献为:
(33)
从式(33)中可以看出与大尺度散射加权项同样是大尺度波的轨道速度,而不是文献[9]中提到的“镜面散射点”的漂流速度,“镜面散射点”的漂流速度通常要远远大于波浪的轨道速度。因此文献[9]高估了大尺度波对多普勒的贡献。
从上面的分析可以看出双尺度模型给出的多普勒速度只是考虑了全谱模型中|K|≪kb和|Kx|≈kb(kb=2kh为Bragg波数)的情况,而大量的中尺度波谱的积分项被忽略了,但实际上这些忽略部分对多普勒中心频率有显著的贡献。通过下面的仿真分析可以看出中尺度波谱有显著的贡献,相同情况下全谱模型得到的多普勒中心与双尺度模型得到的多普勒中心有较大的差距。
2 仿真分析
下面通过仿真来分析不同谱分量的贡献,定义m(Kx)为:
A(Kx,Ky)[σ′(2kh+Kx,Ky)-σ′(2kh-Kx,-Ky)]dKy
(34)
m(Kx)就反映了雷达入射方向不同谱分量的贡献,在下面的仿真中,采用Plant介绍的“D谱”作为波浪谱模型进行仿真。图1~图4给出了L、C、X 3种波段下不同风速、不同风向的m(Kx)分布。
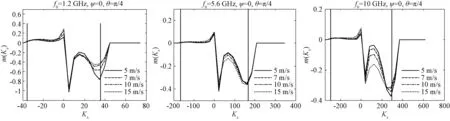
图1 雷达逆风入射时的m(Kx)分布

图2 雷达入射方向与风向夹角45°时的m(Kx)分布
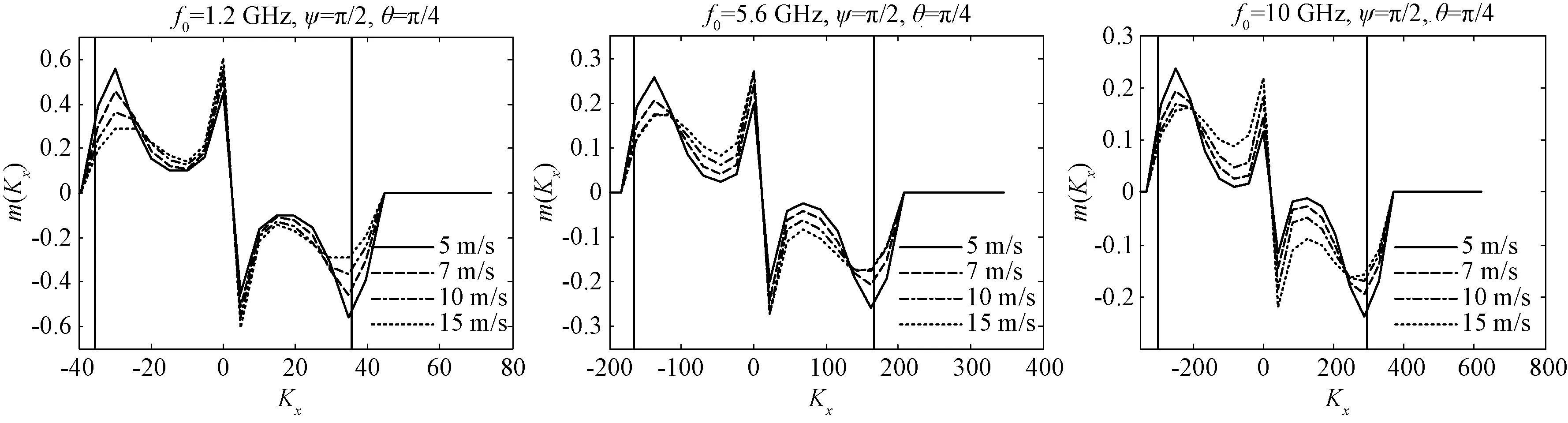
图3 雷达入射方向与风向夹角90°时的m(Kx)分布
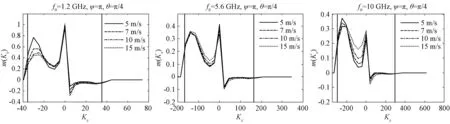
图4 雷达入射方向与风向夹角180°时的m(Kx)分布
图中f0为雷达电磁波频率,ψ为雷达入射方向在海面的投影与风向夹角,θ为雷达入射角,图中2条竖线标注的是正向和反向传播的Bragg波数。
从上面的图可以看出,除了Kx≪Kb以及Kx≈±Kb的分量外,其他波谱分量的贡献也非常明显,并不能简单地采用双尺度模型进行简化,尤其是当Kx<0时,m(Kx)的极值点并不出现在Kx=-Kb的地方,而是出现在略高于Kx=-Kb的位置。
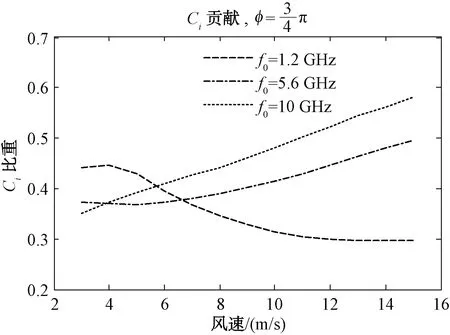
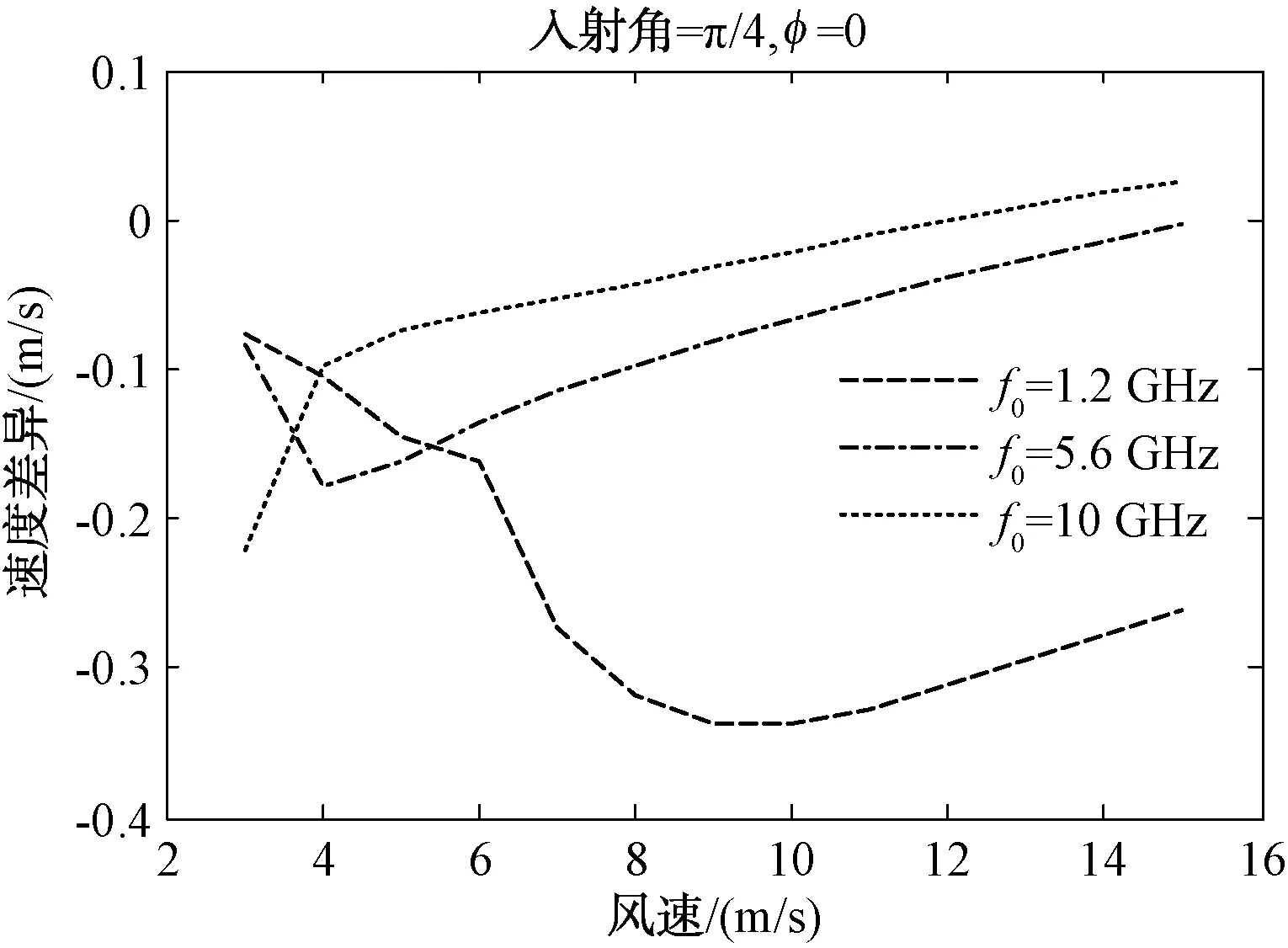
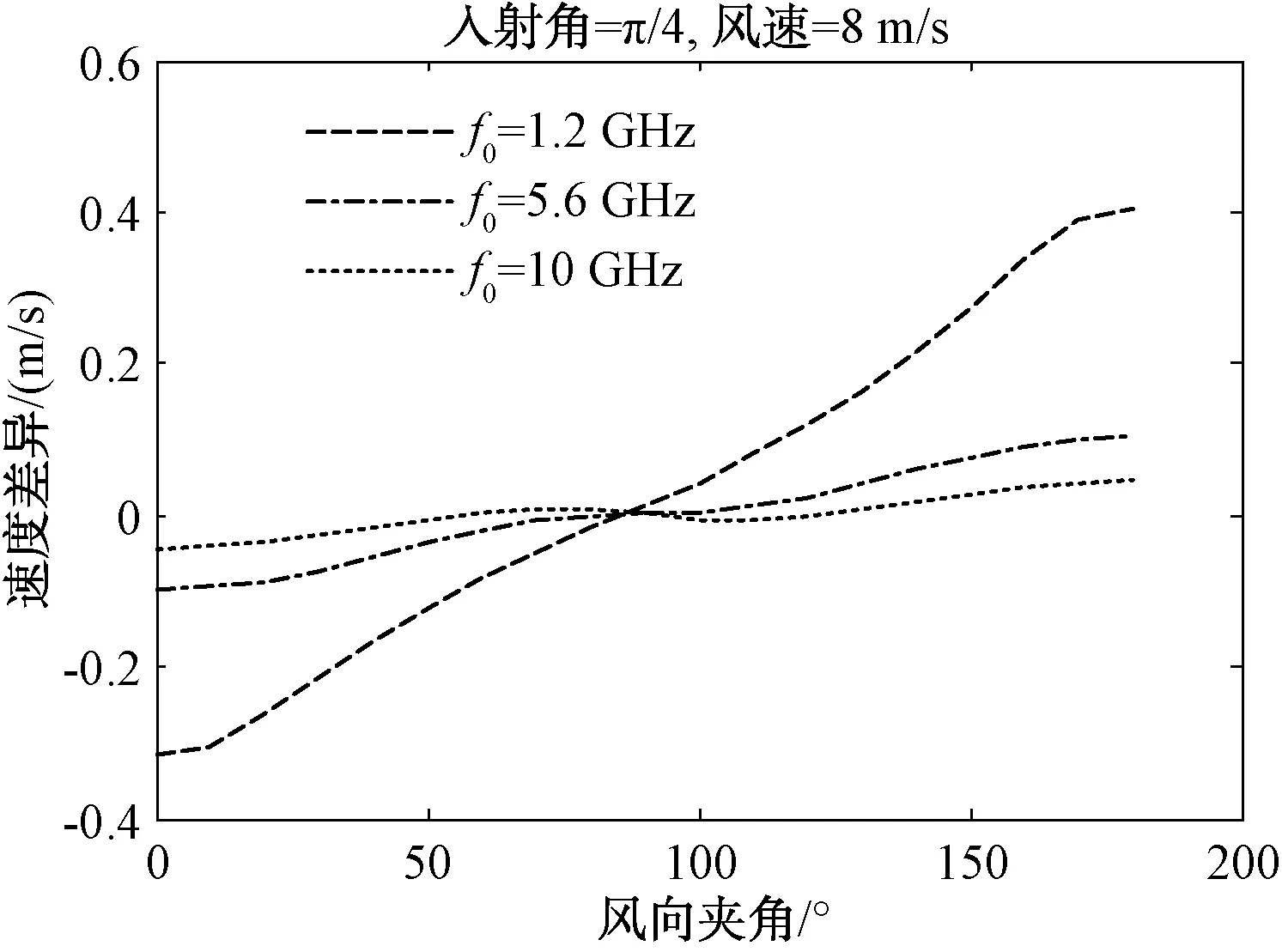
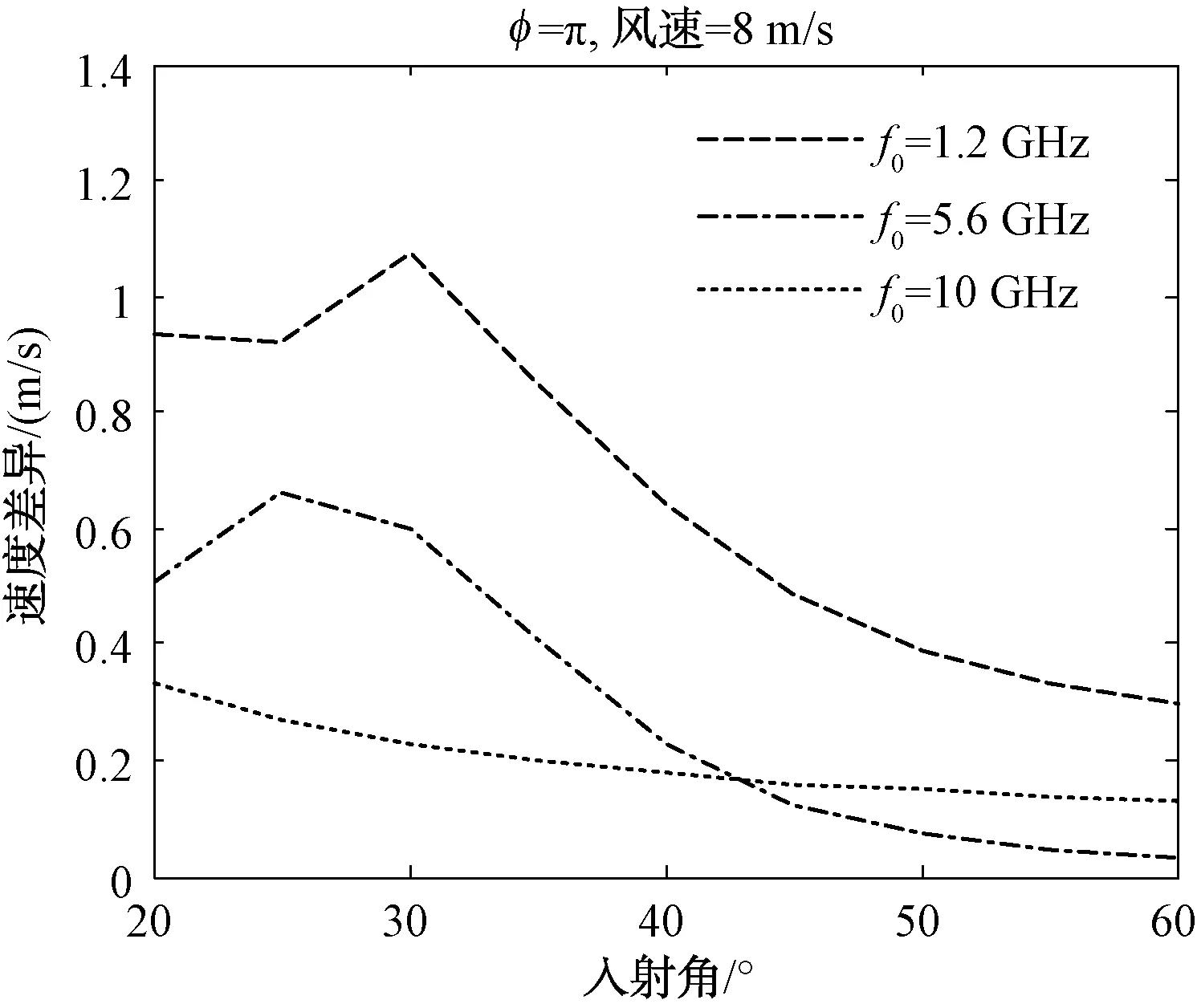
将|Kx| 图5 雷达逆风入射 图6 雷达入射方向与风向夹角45° 图7 雷达入射方向与风向夹角135° 图8 雷达顺风入射 从上图可以看出,中尺度波的贡献在高风速、高波段情况下可以达到50%以上,大部分情况下在30%~50%之间。所以双尺度模型忽略中尺度波的贡献会导致较大的误差。 由于多普勒中心估计与海面流场速度估计有关,下面的仿真中我们对比2种模型多普勒中心计算的多普勒速度差异。多普勒速度差异的定义为: (35) 式中:θ为入射角;λ为波长;Cd_full为采用全谱模型仿真的多普勒中心;Cd_2scale为采用双尺度模型仿真的多普勒中心。 在双尺度模型的仿真中采用的分割尺度为kb/10,其中kb是Bragg波数。图9~图11给出了不同风速和雷达参数条件下的多普勒速度差。 图9 全谱模型和双尺度模型在不同风速的多普勒速度差异 图10 全谱模型和双尺度模型在不同风向夹角下的多普勒速度差异 图11 全谱模型和双尺度模型在不同视角的多普勒速度差异 从上面的图中可以看出采用双尺度模型仿真的多普勒中心与全谱模型计算的多普勒速度有显著差异,在L波段最大可能导致1 m/s的速度差异,对于C和X波段来说最大可能导致约0.2~0.4 m/s,这个速度误差对于高精度的海流估计是不能忽略的。 本文给出了一种基于解析表达的海面波浪多普勒中心全谱模型,该模型涵盖了全部谱分量的作用,在理论上比传统基于双尺度模型的多普勒中心模型更严格和精确。对多普勒中心全谱模型的深入分析表明,如果只考虑波浪谱中|K|≪2kh以及Kx≈2kh两部分谱的贡献,经过一些近似,全谱模型可以化简为双尺度模型,双尺度模型忽略了大量的中尺度波谱的贡献。仿真表明,中尺度波在高风速高波段情况下的贡献超过50%,大部分情况下中尺度谱分量的贡献占整个多普勒中心的30%~50%,因此如果采用双尺度模型简化会导致较大的误差。对于L波段来说,双尺度模型仿真的多普勒中心与全谱模型的差异最大可以导致1 m/s的海面速度差异,对于C和X波段来说最大可能导致约0.2~0.4 m/s的差异,这个速度差异对于高精度的海流估计也是不能忽略的。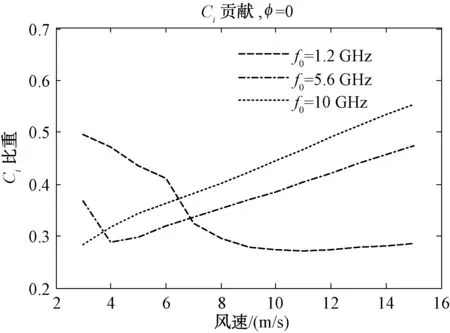


3 结束语

