网格圈负压式集聚纺须条半自由端加捻模型
傅 婷, 陈南梁
(东华大学 纺织学院,上海 201620)
网格圈负压式集聚纺纱的实践表明,在同等工艺条件下,使用同种原料纺制相同线密度的纱线时,集聚纱的捻度比环锭纱的捻度高3%~10%。前期研究[1-3]认为集聚区须条同时存在假捻和真捻。杨兴等[1]率先提出将增加的捻度称之为附加捻度。 周水平等[4-5]对附加捻度进行了研究,结果表明该附加捻度的数值与纤维原料、集聚负压、集聚斜槽的长度及倾斜角度等有关。经典的加捻理论认为环锭纺的加捻属于典型的非自由端加捻,集聚纺与环锭纺的加捻方式是一致的,两者的区别在于集聚纺在环锭纺的前罗拉输出处增加了一个集聚区。按照非自由端加捻理论,集聚区须条加捻处应该是假捻而非真捻。关于附加捻度形成机理的研究并不多,杨建平等[6]对集聚区的气流流动进行了建模研究,分析了负压、集聚槽等对气流分布的影响,但是未对纤维的运动进行分析。Wang等[7]建立了集聚区的流场模型,并分析了纤维的运动轨迹,但没有说明附加捻度产生的机理。杨建平等[8]提出了半自由端加捻模型,认为在集聚区须条存在打滑现象,因而在假捻过程中会产生捻度差异,形成所谓的附加捻度,但是仍没有清晰地解释附加捻度的形成原因。陆宗源[9-10]提出了表层半开端加捻的模式,认为须条表面有部分纤维在气流的作用下发生加捻,但也未进行理论分析和试验验证。本文对网格圈负压式集聚纺集聚区须条进行分析,提出了半自由端加捻机理,并对单纤维进行运动建模和求解,最后进行试验验证,为附加捻度的形成和集聚机理提供依据。
1 须条半自由端加捻机理
集聚区须条两端被握持,从形式上看属于典型的非自由端加捻,而实际上须条在集聚管上因摩擦而出现的加捻属于假捻,因此对成纱捻度几乎无影响。然而附加捻度的存在表明在集聚区上须条的确是有真捻产生的。受喷气纺包缠加捻模式的启发,本文认为集聚区的须条可以分为两部分:一是须条的表层纤维,其一端被钳口握持或被其他纤维控制,另一端则呈自由状态;二是须条的主体纤维,其两端均处于被握持或被控制的状态。在不考虑假捻的情况下,集聚纺中具有自由端的表层纤维在气流等的作用下对主体纤维须条进行了包缠加捻,从而使得须条从扁平状集聚为近似圆柱状。这样的须条结构再经过钢领钢丝圈加捻,最终形成集聚纱。

图1 集聚区须条半自由端加捻模型示意图Fig.1 Schematic diagram of the semi-open-end twisting insertion model of fiber strand in the condensing zone
集聚区须条的加捻可认为是半自由端加捻,其模型示意图如图1所示。表层纤维呈自由端状态,在气流的作用下表层自由端纤维包缠主体纤维形成捻度;而主体纤维仍然呈非自由端状态,在不考虑假捻情况下,其应该呈无捻状态,因此纱线结构呈现为皮芯结构。集聚区须条皮芯结构效果图如图2所示。

图2 集聚区须条皮芯结构示意图Fig.2 Schematic diagram of the skin-core structure of fiber strand
进一步需要讨论的问题有两个:一是须条中具有自由端的表层纤维是如何包缠内层主体纤维的,加捻程度如何;二是皮芯结构中,表层自由端纤维与内层主体纤维的比例究竟是如何分配的。本文主要讨论第一个问题。
2 单根纤维半自由端运动模型
纤维在集聚区的运动和受力情况十分复杂。前人的研究基本以须条整体或微元段为对象[11-12],展现的是须条的宏观特性。本文以集聚区须条中具有自由端的纤维为研究对象,在直线型集聚槽上进行建模分析。
自由端纤维的一端被钳口或者其他纤维所握持,另一端在气流的作用下运动。由于纤维在流场中的运动十分复杂,为简化计算,假定单纤维由一串一定质量的球体组成,每个球体的直径即为纤维截面的直径,计算单个纤维球体在坐标体系的三维坐标值,即可近似得出纤维的运动轨迹。
每个纤维球的质量mf为
(1)
式中:ρf为纤维线密度;df为纤维直径。
由纤维的一端受须条握持和另一端在空气中自由运动可知,纤维主要受空气阻力和须条握持力的作用,单个纤维球体的受力状况也是如此。自由端纤维球受力分析图如图3所示,建立Oxyz坐标系,须条运动方向与网格圈运动方向形成的夹角为β,须条运动方向与斜槽方向相一致。集聚斜槽与集聚管垂直面的夹角也为β。

图3 集聚区纤维的受力分析图Fig.3 Force diagram of the fiber in the condensing zone
2.1 空气阻力
空气阻力Fd如式(2)所示。
(2)
式中:CD为空气阻力系数;ρa为空气密度;Af为纤维球正对来流的最大截面积;va为空气速度;vf为纤维球体速度。
空气阻力系数CD是与雷诺数相关的常数,由式(3)可得。
(3)
式中:σ为介于0.40~0.45之间的常数。
雷诺数Re定义为
(4)
式中:μ为空气运动黏度。
在笛卡尔坐标系Oxyz中,将空气阻力分解为x,y,z3个方向的分力,分别为
(5)
(6)
(7)
2.2 须条握持张力
T表示纤维受到须条握持力,即集聚须条在运动方向上所受到的张力(N);f1为集聚须条在z轴方向受到的摩擦力(N);f2为集聚须条在x轴方向受到的摩擦力(N);f为集聚须条受到的总摩擦力(N);N为网格圈对集聚须条单位面积上的法向支持力(N);P为集聚须条受到集聚气流的作用力(N);p为集聚气流的压强(Pa)。
沿z轴方向取力的平衡方程式,可得
T=f1
(8)
沿y轴方向上取力的平衡方程式,可得
N=p×As
(9)
式中:As为须条受压面积。
集聚区中纤维受到的摩擦力的分解示意图如图4所示,其中,v纱为须条运动速度,v网为网格圈运动速度,Δv为合速度。
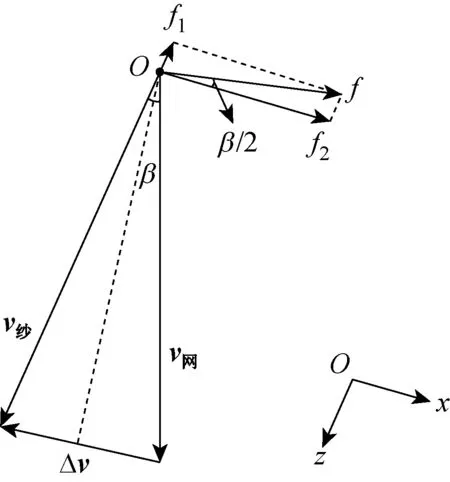
图4 集聚区纤维受到的摩擦力分解示意图Fig.4 Schematic diagram of factorization of frictional force on fiber in the condensing zone
根据图4中摩擦力的分解示意图,可得总摩擦力f与f1的关系为
(10)
又
f=μfN
(11)
根据式(8)~(11)可得
(12)
因此,根据牛顿第二定律,可得一端受握持的纤维球在空气中的运动方程为
(13)
式中:(xf,yf,zf)为纤维在t时刻的位置。
2.3 计算方法与步骤
(1) 给定初始时刻(t=0)时,纤维球的初始速度和初始位置,集聚斜槽的倾斜角度β,须条受压面积As;
(2) 根据式(3)~(7)计算得到纤维球所受到的空气阻力;
(3) 根据式(8)~(12)计算得到纤维球所受到的须条握持力;
(4) 根据式(1)和(13)计算得到纤维球在t+Δt时刻的位置;
(5) 重复步骤(2)~(4),可求得纤维球随时间发展的运动轨迹。
3 模拟结果分析与验证
本文以纺制线密度为15.3 tex的棉集聚纱为例进行计算和验证,相关参数如下:棉纤维线密度为0.18 tex,棉纤维直径为20 μm,棉纤维体积密度为1.54×103kg/m3,流场分布以文献[6]的方法计算获得。纺纱的其他工艺参数如表1所示。

表1 纺纱工艺的参数设计Table 1 Parameters design of spinning process
需要说明的是,表1中集聚槽的倾斜从上往下为向右倾斜,即呈“/”状,其附加捻度为Z捻,与成纱捻向是一致的,因而成纱的最终捻度是增加的。从以上分析可以看出,捻向与集聚槽倾斜方向有关。
按照第2节所述的模型和计算方法,得到单根自由端纤维的运动轨迹如图5所示。从图5中可以看出集聚槽倾角分别为5°和10°时自由端纤维的运动轨迹。根据捻度的定义,即须条在单位长度的捻回数可知,由于须条上存在捻回传递,每一段的捻度可能存在差异,故本文依据轨迹得到的第一个捻回对应的须条长度进行捻度计算,可以得出集聚槽倾角分别为5°和10°时其第一个捻回对应的长度分别为16和12 mm,因此其附加捻度的计算值分别为62.5和83.3捻/m。


(a) 集聚槽倾角为5° (b) 集聚槽倾角为10°图5 自由端纤维在集聚区的轨迹图Fig.5 Schematic diagram of the trajectories of open-end fiber
按照表1的条件,采用集聚槽倾角为5°的集聚管进行纺纱验证,实际得到的附加捻度为50捻/m,可见计算值与试验值还是比较吻合的。当然还有一定的数值差距,本研究认为可能存在的原因有:(1)附加捻度应该与自由端纤维的根数有关;(2)用某一个纤维球体在坐标体系的运动轨迹来表示与实际有一定差异,需要进一步细化纤维的模型。但是总体而言,本文模型可以解释集聚区须条的半自由端加捻,并能够很好地分析附加捻度的形成机理,为深入研究集聚机理提供依据。
4 结 论
(1) 本文提出了网格圈负压式集聚纺“半自由端加捻”模型,认为集聚区须条表面存在部分自由端纤维,在气流等作用下,表层纤维对主体纤维进行包缠加捻,形成皮芯结构。该模型解释了附加捻度的形成机理。
(2) 对单根自由端纤维进行力学建模及运动学分析,并可通过计算单个纤维质量球体的三维坐标值近似得到纤维运动轨迹。通过模拟计算结果与试验值的对比分析,验证了模型的正确性。

