时间序列模型在桥梁健康监测数据预测中的应用

陆 萍 王 涛 韦 跃 李 竞 吴海军

(1. 重庆交通大学土木工程学院， 重庆 400074； 2. 江苏交科交通设计研究院有限公司， 江苏 苏州 223001；3. 重庆市沙坪坝区公路养护中心， 重庆 400030)

时间序列是指对某一个统计指标在各个时间上的不同数值依时间顺序排列而形成的序列[1]。通过时间序列分析，可以发现事物运动、变化和发展的内在规律，对于人们正确认识事物并做出科学的决策具有重要的意义[2]。桥梁健康监测系统中采集的数据符合时间序列的定义，大量的监测数据需要得到及时处理[3]。桥梁健康监测数据分析方法有2种:一是依据数据量值的大小及范围来判断当前结构的状态，或者进行预警，指导桥梁的日常养护管理；二是依据现有的监测数据规律来预测数据的变化趋势，预先估计桥梁结构的状态，及早规划桥梁的养护策略[4]。本次研究主要通过基于时间序列预测模型对桥梁健康监测数据发展趋势进行预测，并结合江津长江大桥的工程应用实例进行分析。

1 时间序列预测模型分析流程

时间序列分析属于定量预测，通过分析数据的规律来预测事物的未来发展趋势。由于事物发展具有随机性，可能会受到偶然因素的影响，因此可采用统计分析方法对历史数据进行预处理[5]。

桥梁是一种大体量结构体，在结构疲劳损伤和外部荷载的作用下，结构的短期响应平稳，长期响应不平稳。通过桥梁健康监测，可采集到关键截面的挠度，并形成时间序列。其中，决定结构长期变化的任一变量的时间序列，均包含了结构全部变量长期变化的信息。因此，在桥梁健康监测系统的所有测点中，可以选择具有代表性的测点进行研究，并形成时间序列。利用时间序列分析理论对监测数据进行处理，运用数值分析软件Matlab建立时间序列模型，可有效分析和处理监测数据[6]。

时间序列模型的数据分析处理流程如下：

(1) 数据预处理。剔除数据异常值和错误，对于部分缺失数据可以利用插值法补入。

(2) 平滑处理。通过平滑处理来消弱干扰信号及信号中的不规则趋势项，使得数据的长期变化规律更明显。

(3) 平稳化处理。对时间序列进行分解，含有趋势项和周期项的序列可以通过差分处理实现平稳化。

2 时间序列预测模型的建立

在此，采用了波克斯-詹金斯建模方法[7-8]。首先利用自相关系数和偏自相关系数分析识别模型的类型，然后估计模型参数和模型阶数，最后进行模型的适用性校验及数据预测。

2.1 模型的识别

表1 三种时间序列模型的性质

2.2 模型的定阶

2.2.1 模型定阶的AIC准则

AIC准则由日本统计学家Akaike于1973年提出。AIC准则的全称为最小信息量准则，即当信息量取最小值时模型为最优[9]。AIC准则函数是评价综合最优配置的指标，是拟合精度和未知参数的加权函数。AIC准则的函数如式(1)所示：

(1)

可以看出，AIC准则函数可分为2部分：第一部分表示模型拟合度，它随着模型阶数的增大而变小；第二部分表示模型参数的数量，其值随着阶数的增大而增大。

2.2.2 模型定阶的BIC准则

AIC准则的不足之处是，如果时间序列很长，相关信息会变得分散。为了改进AIC准则的不足，Akaike在1976年提出了BIC准则。BIC准则的函数如下：

(2)

某一阶数p0满足函数，则：

(3)

式中：pn是阶数上限；p0为最佳阶数。

2.3 模型的参数估计

线性模型：

yi=β1xi1+β2xi2+…+βnxin+εi(1≤i≤N)

(4)

其中y1,y2,…,yn为观测数据，自变量xi1,xi2,…,xin。已知，β1,β2,…,βn是待估计参数，εi是不相关的零均值误差，式(4)可以写成式(5)：

Y=Xβ+ε

(5)

使误差平方和达到最小：

(6)

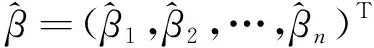
2.4 模型的检验

通过模型检验可判断出模型的拟合程度。时间序列预测模型的检验常采用χ2检验法。

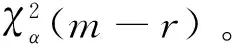
3 工程应用

3.1 工程概况

江津长江大桥于1997年建成通车。大桥分为主桥和引桥部分，全桥长度为1 360 m。其中，主桥为140 m+240 m+140 m的连续刚构桥；重庆岸引桥采用14×50 m 简支T梁桥，江津岸引桥采用4×22.5 m心板梁桥。主桥断面为单箱单室箱型截面，底板宽11.5 m，顶板宽22 m，设置1.5%的横坡。主桥跨和边跨现浇段箱梁高为4 m，墩顶处箱梁高13.5 m。主桥桥墩为双薄壁墩。

3.2 挠度监测系统

3.3 时间序列预测模型的建立

为保证时间序列模型的可信度和可靠性，建模前应对监测数据进行预处理。为了检验序列的随机性，需测试处理后序列的正态性。利用Matlab软件绘制时间序列直方图 ，如图4所示。

由时间序列直方图可知，时间序列符合正态分布。计算时间序列在95%置信度下的偏自相关系数和自相关系数，结果如图5、图6所示。

图1 挠度监测系统立面图

图3 B-B截面(主跨14)激光布置图

由图5、图6可知，时间序列的自相关系数和偏自相关系数都是拖尾的，因此可采用ARMA模型进行预测。利用Matlab中的AIC、BIC命令，求解不同的p、q值对应的AIC、BIC值，结果见表2。

由上可知，当p=2和q=3时，AIC和BIC取得最小值，p和q即为真阶，因此时间序列预测模型为ARMA(2,3)。

图4 时间序列直方图

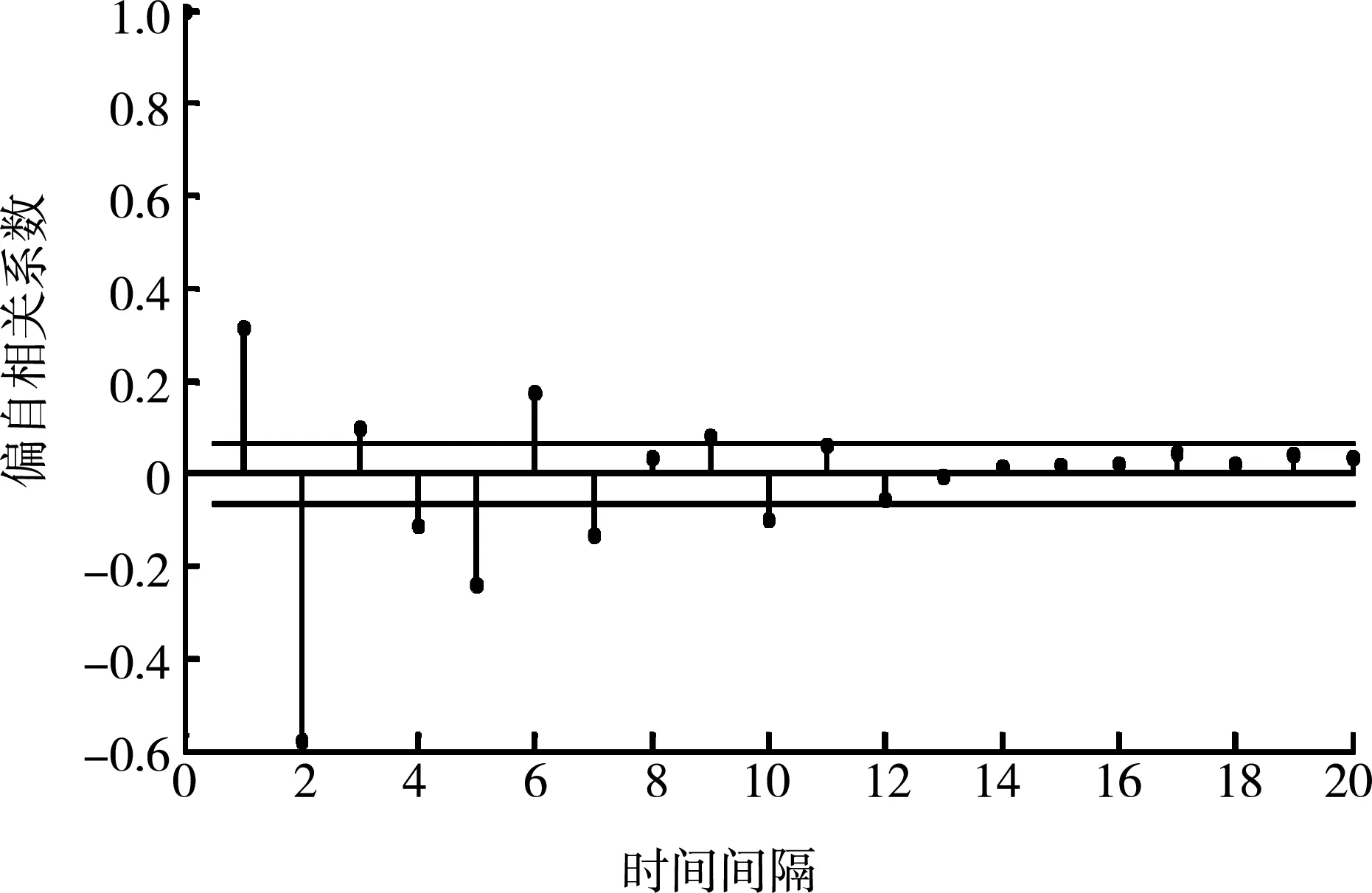
图5 时间序列偏自相关系数图

图6 时间序列自相关系数图

时间序列预测模型ARMA(2,3)的参数估计值可利用Matlab中的Garchset和Garchfit命令求出结果：

θ=[0.560 5，-0.147 3，-0.483 1]

φ=[0.056 9，-0.222 3]

式中，θ和φ分别为自回归系数和滑动平均系数。

表2 不同p和q对应的AIC和BIC值

时间序列模型建立后，需对模型的拟合优度进行检验。采用χ2检验法，利用Chi2gof等命令对时间序列模型的残差白噪声进行检验。检验结果显示，H0=0，残差均值为0.008 2，约为0。因此，模型的残差符合零均值的正态分布，表明模型通过检验。

3.4 ARMA模型预测

通过模型的适用性检验后，可将该模型应用于挠度监测数据的预测，对挠度监测数据的80个步骤进行预测。利用Matlab平台中的Garchpred和其他命令，可以得到时间序列模型的挠度预测值。模型预测值与实际监测值对比如图7所示。

图7 挠度预测值和监测值对比图

由于数据较多，仅提取最后10组数据来检验模型的预测精度，挠度预测值和监测值见表3。

表3 挠度预测值和监测值

由上述分析可知，利用ARMA(2,3)模型能够预测未来一段时间的挠度监测数据，相对误差也在工程实践的可接受数值范围之内。

4 结 语

通过建立时间序列模型，对江津长江大桥挠度监测数据进行了分析和预测。运用时间序列模型，能够拟合桥梁监测数据的变化趋势，并根据其趋势规律预测未来一段时间的挠度监测数据。本工程时间序列模型预测趋势基本符合实测样本，并且短期预测精度相对较高，可应用于工程实践。合理运用时间序列分析方法，有助于桥梁健康监测数据的预测分析。