L-集上的模糊泛代数

魏晓伟, 岳跃利*, 黄春娥

(1. 中国海洋大学 数学科学学院, 山东 青岛 266100; 2. 北京联合大学 生物化学工程学院, 北京 100023)

泛代数在数学和计算科学领域起到了十分重要的作用.模糊方法用于研究泛代数的结构开始于Rosenfeld的模糊群[1].从此,许多作者开始研究模糊泛代数理论[2],比如Murali基于经典的泛代数理论通过Zadeh扩张原理来研究模糊泛代数.Bošnjak等[3]等在完备剩余格的环境下,研究两类模糊集上的泛代数;Demirci[4]提出模糊函数和伴有多值等价关系的模糊代数概念的理论;Shi[5]研究模糊关系和模糊子群的性质;Qiu等[6]研究了基于等价关系的模糊数的商空间的代数性质和拓扑性质.这里想强调的是,已经存在的模糊泛代数理论是基于经典集合的,那么一个很自然的问题就是,模糊集上的模糊泛代数理论是什么样的呢？这正是本文的出发点.

1 预备知识

设(L,*)是quantale,如果存在一个元素e且满足对于任意的α∈L均有e*α=α成立,则称(L,*)是单位的quantale.→:L×L→L是相对于*的右伴随且计算式为:α→β=∨{γ∈L|α*γ≤β},如果对于任意的α,β∈L,有α∧β=α*(α→β)成立时,称(L,*)为可除的[7].本文在交换、可除的单位quantale环境下进行讨论.

L-集A是从集合A0到L的映射,集合A0称为A的定义域,值A(x)为x属于A的程度.

定义1.1[8]设A:A0→L和B:B0→L是2个L-集.如果R:A0×B0→L满足对于任意的x∈A0,y∈B0,有R(x,y)≤A(x)∧B(y)成立,则称R:A⇀B为L-值关系.

定义1.2[8]设A是L-集,R:A⇀A是L-值关系:

1) 如果x∈A0,有A(x)≤R(x,x)成立,则称R是A上自反的;

2) 如果x,y,z∈A0,有

R(x,y)*(A(y)→R(y,z))≤R(x,z)

成立,则称R是A上传递的;

3) 如果x,y∈A0,有R(x,y)=R(y,x)成立,则称R是A上对称的;

4) 如果x,y∈A0,由

R(x,x)=R(x,y)=R(y,x)=R(y,y)⟹x=y,

则称R是A上分离的.

同时,如果R满足自反和传递,称R是A上L-值预序,序对(A,R)称为L-值预序集;如果R满足自反、对称和传递,称R是A上L-值等价,序对(A,R)称为L-值集;如果R满足自反、分离和传递,称R是A上L-值偏序,序对(A,R)称为L-值偏序集.

在文献[9]中,对于L-集A,它的幂集P(A):P(A)0→L还是L-集,其中

P(A)0={(f,δ)|f≤A∧δ},

且

P(A)(f,δ)=δ.

SA:P(A)⇀P(A)定义为

SA((f,δ),(g,ε))=

可以验证SA是P(A)上的L-值偏序.

类似于文献[10],设R:A⇀B是L-值关系,σ(R):B⇀B定义为

σ(R)(y1,y2)=SA((R(-,y1),B(y1)),

(R(-,y2),B(y2))),

则σ(R)是B上的L-值预序,且R是B上的L-值预序当且仅当σ(R)=R.

对于2个L-集A和B,映射α:A→B,如果对于任意的x∈A0,有A(x)=B(α(x))成立,则称α是程度保持映射.下面定义L-集上的闭包算子.

定义1.3[9]设P(A)是A上的L-值幂集.映射cl:P(A)0→P(A)0满足以下的条件:

(C1)SA((f,δ),(g,ε))≤SA(cl(f,δ),cl(g,ε));

(C2) (f,δ)≤cl(f,δ);

(C3) cl(cl(f,δ))=cl(f,δ),

则称cl:P(A)0→P(A)0是P(A)上的L-值闭包算子.

设R:A⇀A是L-值关系,Rl:P(A)→P(A)和Ru:P(A)→P(A)定义为

Rl(f,δ)=(Rl(f),δ),

且Rl(f):A0→L定义为

类似Ru(f,δ)=(Ru(f),δ),且Ru(f):A0→L定义为

定理1.4设R:A⇀A是A上的L-值关系,则R是L-值预序当且仅当Ru:P(A)→P(A)是P(A)上的L-值闭包算子,当且仅当Rl:P(A)→P(A)是P(A)上的L-值闭包算子.

证明证明过程与分明集上的L-关系[8]证明类似,故省略.

类似于文献[11],将L-值关系R:A⇀A提升到相对应的幂集R→:P(A)⇀P(A),R←:P(A)⇀P(A),R+:P(A)⇀P(A),有

R→((f,δ),(g,ε))=SA((f,δ),(Rl(g),ε)),

R←((f,δ),(g,ε))=SA((g,ε),(Ru(f),δ)),

和

R+((f,δ),(g,ε))=

R→((f,δ),(g,ε))∧R←((f,δ),(g,ε)).

定理1.5设A是L-值集,则以下的结论是等价的:

1)R:A⇀A是A上L-值预序⟺R←是P(A)上L-值预序;

2)R:A⇀A是A上L-值预序⟺R→是P(A)上L-值预序.

证明证明过程与分明集上的L-关系[8]证明类似,故省略.

2 L-集上的模糊泛代数

首先看模糊集A的n-次幂的定义形式.考虑切片范畴Set↓L的对象的乘积.任取A,B∈Set↓L,那么有[A,B]Set↓L={φ:A0|→B0},这里φ是程度保持映射.所以A×B:(A×B)0→L定义为

(A×B)(x,y)=A(x)=B(y),

其中

(A×B)0={(x,y)∈A0×B0|A(x)=B(y)}.

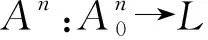
An(x1,x2,…,xn)=

A(x1)=A(x2)=…=A(xn),

其中

A(x2)=…=A(xn)}.

A上的n-元运算就是从An到A的程度保持映射.

本文中,总假设对于任意的x∈A0,有A(x)≠0成立.

定义2.1设A:A0→L是L-集,并且F是A上n-元运算的集合,则序对A=〈A,F〉称为A上的模糊泛代数.

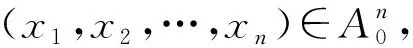
φ(f(x1,x2,…,xn))=f(φ(x1),φ(x2),…,φ(xn))

时,则称φ是从A到B的同态映射.若同态映射φ是单射,则称φ为嵌入映射.若同态映射φ是双射,则称φ为同构映射.

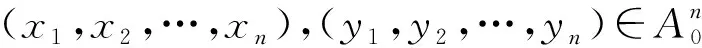
R(x1,y1)*(A(x2)→R(x2,y2))*…*

(A(xn)→R(xn,yn))≤

R(φ(x1,x2,…,xn),φ(y1,y2,…,yn))

成立,则称R是A上的相容关系.特别地,A上相容的L-值等价关系称为A上的同余关系.

设〈A,F〉是模糊泛代数,R是A上的同余关系.可以定义模糊商代数〈A/R,F/R〉.定义A/R:(A/R)0→L为(A/R)(x/R)=A(x),其中

(A/R)0={x/R|x∈A0},

且

x/R={y∈A0|R(x,x)=

R(y,x)=R(x,y)=R(y,y)}.

定义f/R:(A/R)n→A/R为

(f/R)(x1/R,x2/R,…,xn/R)=f(x1,x2,…,xn)/R.

设A=〈A,FA〉和B=〈B,FB〉是相同型的模糊泛代数,α:A→B是同态映射,定义α的核ker(α):A⇀A为

∀x,y∈A0,ker(α)(x,y)=

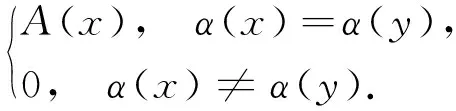
易知ker(α)是A上的同余关系且有如下的同构定理.

定理2.4(第一同构定理) 设A和B是同型的泛代数,α:A→B是满同态映射,则

A/ker(α)≅B.

设A是模糊泛代数,θ和φ是A上的2个同余关系且θ≤φ.定义A/θ:(A/θ)0→L为(A/θ)(x/θ)=A(x),其中

(A/θ)0={x/θ|x∈A0}.

同时定义φ/θ:(A/θ)⇀(A/θ)为

(φ/θ)(x/θ,y/θ)=φ(x,y),

则可以验证φ/θ的定义是合理的并且是A/θ上的同余关系.

定理2.5(第二同构定理) 设A是泛代数,θ和φ是A上的2个同余且θ≤φ,则

(A/θ)/(φ/θ)≅A/φ.

设B是A的模糊子代数,θ是A上的同余关系.定义Bθ:(Bθ)0→L为

其中

Bθ=A|(Bθ)0,

且

(Bθ)0={x∈A0|B0∩x/θ≠∅}.

实际上,可以证明〈Bθ,F〉是B的模糊子代数,θBθ是Bθ上的同余关系.

定理2.6(第三同构定理) 设B是A的模糊子代数,θ是A上的同余关系,则

B/θB≅Bθ/θBθ.

关于以上3个同构定理的证明,可类似参考经典集上的泛代数[12]中分别对应的同构定理的证明方法.

3 L-值幂代数

设A=〈A,F〉是模糊泛代数.对于θ:An→A,θ+:P(A)n→P(A)定义为

其中

为

其中

则称P(A)=〈P(A),{θ+|θ∈F}〉为〈A,F〉的L-值幂代数.

相应的修改传递性如下:一个L-值关系R如果满足对于任意的x,y,z∈A0且A(x)=A(y)=A(z)有

R(x,y)*(A(y)→R(y,z))≤R(x,z),

称R为弱传递.类似的定义：

和

其中

Ay={x∈A0|A(x)=A(y)}.

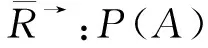
在这种情况下,定理1.4和定理1.5均成立.

定理3.1设〈A,F〉是模糊泛代数,R是A上的弱L-值预序,则以下陈述是等价的:

1)R是A上的相容关系;

2)R→是P(A)上的相容关系;

3)R←是P(A)上的相容关系.

证明仅证明1)⟺2),1)⟺3)可类似证明.

1)⟹2) 假定θ∈F,(fi,δ),(gi,δ)∈P(A)0,因为

(A(y1)→R(θ(x1,x2,…,xn),θ(y1,y2,…,yn))),

并且有

所以

成立.考虑到

R→(θ+((f1,δ),(f2,δ),…,(fn,δ)),

θ+((g1,δ),(g2,δ),…,(gn,δ)))=

然后有

R→((f1,δ),(g1,δ))*

(δ→R→((f2,δ),(g2,δ)))*…*

(δ→R→((fn,δ),(gn,δ)))≤

故R→具有相容关系.

R(x1,y1)*(A(x2)→R(x2,y2))*…*

(A(xn)→R(xn,yn))=

R→((Ax1,A(x1)),(Ay1,A(y1)))*…*(A(xn)→

R→((Axn,A(xn)),(Ayn,A(yn))))≤

R→(θ+(((Ax1),A(x1)),…,(Axn,A(xn))),

θ+(((Ay1),A(y1)),…,((Ayn),A(yn))))≤

A(xi)=SA((Axi,A(xi)),(Ayi,A(yi)))≤

R(θ(x1,x2,…,xn),θ(y1,y2,…,yn)).

所以,R具有相容性.

定理3.2设A是模糊泛代数且R是A上的同余关系,存在从P(A/R)到P(A)/R+的满同态映射.

证明首先,需要说明(P(A)/R+)0中元素的形式.对于(f,δ)∈P(A)0,如果(g,η)∈[(f,δ)],则有

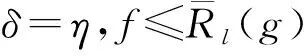
[(f,δ)]={(g,δ)∈P(A)0|f≤

接着,定义θ:P(A/R)→P(A)/R+为

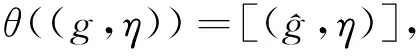
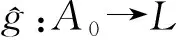
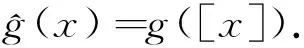
可以验证θ是一个满的程度保持映射.

最后,需证θ是同态映射.设φ是A上n-元运算,任意(gi,η)∈P(A/R)0,有

θ((φ/R)+((g1,η),(g2,η),…,(gn,η)))=

φ+/R+(θ((g1,η)),θ((g2,η)),…,θ((gn,η)))=

因此,去验证

即

成立.剩下的部分很容易去验证,则θ是满同态映射.

推论3.3P(A/R)/ker(θ)≅P(A)/R+,其中θ是定理3.2中的满同态映射.

如果ε(R)是A上的同余,则称R是A上好的关系,其中ε(R)=σ(R)∧σ(R)op;如果R→是P(A)上好的关系,称R是A上Hoare好的关系;如果R→是P(A)上好的关系,称R是A上Smyth好的关系.

定理3.4设A是模糊泛代数且R是A上的弱L-值预序,当*=∧时,则下面的陈述是等价的:

1)R是A上的相容关系;

2)R是A上Smyth好的关系;

3)R是A上Hoare好的关系.

证明只证明1)⟺2).

1)⟹2) 因为R是弱L-值预序关系,所以ε(R←)=R←∧(R←)op,并且R←和(R←)op还是弱L-值预序.ε(R←)具有对称性.由于R是A上的相容性关系,由定理3.1知,R←具有相容性.下面说明ε(R←)具有相容性.对于(fi,δ),(gi,δ)∈P(A)0(1≤i≤n)有

ε(R←)((f1,δ),(g1,δ))∧

(δ→ε(R→)((f2,δ),(g2,δ)))∧…∧

(δ→ε(R←)((fn,δ),(gn,δ))))=

(R→∧(R←)op)((f1,δ),(g1,δ))∧

(δ→((R←)op∧R←)((f2,δ),(g2,δ)))∧…∧

(δ→((R←)op∧R←((fn,δ),(gn,δ))))≤

[R←((f1,δ),(g1,δ))∧

(δ→R←((f2,δ),(g2,δ)))∧…∧

(δ→R←((fn,δ),(gn,δ))))]∧

[(R←)op((f1,δ),(g1,δ))∧

(δ→(R←)op((f2,δ),(g2,δ)))∧…∧

(δ→(R←)op((fn,δ),(gn,δ))))]≤

所以,R是Smyth好的关系.

2)⟹1) 假定xi,yi∈A0且A(xi)=A(yj)(1≤j,i≤n).定义A(x,y)1A(x,y)A:A0→L为

那么,(A(x,y)1A(x,y)A,A(y))∈P(A)0.因为

R←((Ax,A(x)),(A(x,y)1A(x,y)A,A(y)))=

R(x,y),

以及

R←((A(x,y)1A(x,y)A,A(y)),(Ax,A(x)))=

A(x)∧A(y),

那么有

R(x,y)=R(x,y)∧(A(x)∧A(y))=

ε(R←)((Ax,A(x)),(A(x,y)1A(x,y)A,A(y)))

成立.下面说明R具有相容性,

R(x1,y1)∧(A(x2)→R(x2,y2))∧…∧

(A(xn)→R(xn,yn))=

ε(R←)((Ax1,A(x1)),

(A(x1,y1)1A(x1,y1)A,A(y1)))∧

(A(x2)→ε(R→)((Ax2,A(x2)),

(A(x2,y2)1A(x2,y2)A,A(y2)))∧…∧

(A(xn)→ε(R←)((Axn,A(xn)),

(A(xn,yn)1A(xn,yn)A,A(yn)))≤

R(f(x1,x2,…,xn),f(y1,y2,…,yn))))=

A(xi)∧(A(yi)∧(A(yi)→R(f(x1,x2,…,xn),

f(y1,y2,…,yn))))=

R(f(x1,x2,…,xn),f(y1,y2,…,yn))).

说明R具有相容性.