L-序水平一致极限空间

王文静, 方进明

(中国海洋大学 数学科学学院, 山东 青岛 266100)

2002年,Nusser[1]提出概率一致极限空间的概念,这种概率一致极限空间通过加载三角模的实数单位区间中的数,为一致极限空间中的许多概念提供了概率化的描述.同时,也为Florescu[2]的概率一致空间乃至文献[3]意义下的概率极限空间提供了统一的框架.在完全不同的方向上,取真值格L为完备Heyting代数,Jäger[4]发现了文献[5]所提出的L-一致极限空间的“水平空间”,即L-水平一致极限空间.文献[4]的结果表明,这些水平空间为L-一致极限空间提供了新的描述方式,同时也为概率一致空间、概率一致极限空间、过程一致空间提供了统一的视角,因此可以说水平空间类为空间概念的刻画提供了新的量化模型.

作为文献[5]工作的进展,Fang[6]提出L-序拟一致极限空间的概念.L-序拟一致极限空间的合理性在于空间结构保留了它与满层L-滤子的L-包含序的内在联系,而L-一致极限空间却忽略了这种联系.结合文献[6]的工作,在考虑对称性的前提下,本文提出了L-序一致极限空间的概念.本文发现L-序一致极限空间对应的空间范畴除保留好的性质(如笛卡儿闭性)外,其对应的“水平空间”满足本质不同的性质.因此提出了新的空间概念,即L-序水平一致极限空间,并进一步证明了L-序水平一致极限空间范畴与L-序一致极限空间范畴是同构的.因此,L-序水平一致极限空间为L-序一致极限空间提供了新的版本.此外证明了L-序水平一致极限空间范畴恰好是文献[4]中L-水平一致极限空间范畴的双反射子范畴.如此,清楚地确定了文献[5]中L-一致极限空间与本文提出的L-序一致极限空间的关系.

1 预备知识

首先介绍文中必需的完备剩余格以及L-子集的L-包含序的概念.所谓完备剩余格是三元对(L,≤;*),其中(L,≤)是完备格并且有二元运算*和→满足:

(R1) (L,*)为交换的单位半群,其以(L,≤)的最大元┯为单位元;

(R2) 伴随性质,即

α*β≤γ⟺β≤α→γ, ∀α,β,γ∈L.

三元对(L,≤;*)简记作L(其最小元记为⊥).此时,运算*和→分别被称作是L上的张量和蕴涵,其中,蕴涵→可以计算为

α→β=∨{γ∈L|α*γ≤β}, ∀α,β∈L.

在本文中,如无特殊说明,总假设完备格上的交运算∧对任意并是分配的,因此本文所用到的完备剩余格(L,≤;*)是加载了张量*的完备Heyting代数.

设X是非空集.将X上L-子集的全体记作LX,X的幂集记作P(X).L上的偏序结构可以利用点态方式诱导出L-幂集LX上的偏序结构,仍记作≤.按LX上偏序结构,LX的最小元与最大元分别记作⊥X和┯X,LX上的代数运算∧,∨,*,→可以利用L上的相应运算点态地定义来得到.所谓L-子集的L-包含序是一个二元映射SX(-,-):LX×LX→L,计算意义是对任意的(A,B)∈LX×LX,

其中,→是L中的蕴涵运算.值SX(A,B)可解释为A是B的子集程度.下面介绍满层L-滤子的概念及其性质.

定义1.1[7]映射F:LX→L称为非空集X上的满层L-滤子,如果它满足以下条件:

(F1) F(┯X)=⊥,F(┯X)=⊥;

(F2) 对任意A,B∈LX,A≤B⟹F(A)≤F(B);

(F3) 对任意A,B∈LX,F(A)∧F(B)≤F(A∧B);

(Fs) 对α∈L,α*F(A)≤F(α*A).

给定映射φ:X→Y,满层L-滤子F在映射φ下的像记作定义φ⟹(F),φ⟹(F)是Y上的满层L-滤子使得对任意B∈LY,φ⟹(F)(B)=F(φ←(B)),这里φ←(B)=B∘φ.设F和G为乘积集X×X上的满层L-滤子.分别定义映射F-1,F∘G:LX×X→L如下:

F-1(A)=F(A-1), ∀A∈LX×X,

其中(x,y)∈X×X,A-1(x,y)=A(y,x).

由文献[5]中结果知F-1总是X×X上的满层L-滤子,而F∘G是X×X上的满层L-滤子当且仅当f∘g=⊥X×X可推得F(f)*G(g)=⊥.

1) (φ×φ)⟹(F-1)=((φ×φ)⟹(F))-1;

2) (φ×φ)⟹(F)∘(φ×φ)⟹(G)≤(φ×φ)⟹(F∘G);

3) SLX×X(F,G)≤SLY×Y((φ×φ)⟹(F),(φ×φ)⟹(G)).

2 L-序水平一致极限空间

下面将引入L-序一致极限空间的概念,然后确定L-序一致极限空间范畴作为拓扑范畴是笛卡儿闭的.同时,还界定了其对应的“水平空间”所满足的本质性质,由此幸运地获得了新的空间概念,即L-序水平一致极限空间.进一步证明了L-序水平一致极限空间范畴与L-序一致极限空间范畴是同构的.因此,可以说获得了L-序一致极限空间新的版本,即L-序水平一致极限空间.此外,建立了L-序水平一致极限空间范畴恰好是文献[4]中L-水平一致极限空间范畴的双反射子范畴这一深入联系.

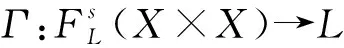
(UC1)Γ([(x,x)])=┯;

(OUC2) SLX×X(F,G)≤Γ(F)→Γ(G);

(UC3)Γ(F)≤Γ(F-1);

(UC4)Γ(F)∧Γ(G)≤Γ(F∧G);

(UC5) 当F∘G存在时,Γ(F)*Γ(G)≤Γ(F∘G).

定理2.2L-序一致极限空间范畴是拓扑的.

当完备剩余格L上的运算*=∧,即L为完备Heyting代数时,用文献[6]的方法可证如下结论.

定理2.3若L为完备Heyting代数,则L-序一致极限空间范畴是笛卡儿闭的.

(LUC1) 对任意x∈X,α∈L,[(x,x)]∈Λ(α);

(LUC2) 当F∈Λ(α)且G≥F时,G∈Λ(α)成立;

(LUC3) F∈Λ(α)总意味F-1∈Λ(α)成立;

(LUC4) 若F,G∈Λ(α),则F∧G∈Λ(α);

(LP1) 当F∈Λ(α)且β≤α时,F∈Λ(β)恒成立;

(LLC) 当A⊆{α∈L|F∈Λ(α)}时,F∈Λ(∨A)成立,则称(X,Λ)为L-水平一致极限空间.L-水平一致极限空间及其一致连续映射构成一个范畴,将其记作L-LULIM,这里所谓映射φ:(X,Λ)→(Y,Σ)是一致连续的是指对任意α∈L,(φ×φ)⟹(Λ(α))⊆Σ(α)成立.

定义2.4若L-水平一致极限空间(X,Λ)还满足

首先指出,由于作为L-序水平一致极限空间本质性质的(LOUC2)总意味着(LUC2),因此L-序水平一致极限空间一定是L-水平一致极限空间.正是这个理由,L-序水平一致极限空间作为对象构成L-水平一致极限空间范畴的满子范畴,本文将其记作L-OLULIM.此外,为进一步探索L-序水平一致极限空间范畴与L-序一致极限空间范畴之间深入的关系,下面给出几个预备性的命题,目的是指出对象转化过程中存在一些规律性.限于篇幅,仅给出命题2.6的证明.

则(X,ΛΓ)∈|L-OLULIM|.

ΓΛ(F)=∨{α∈L|F∈Λ(α)},

则(X,ΓΛ)∈|L-OULIM|.

ΓΛ(F)*SLX×X(F,G)=

(∨{α∈L|F∈Λ(α)})*SLX×X(F,G)≤

∨{(α*SLX×X(F,G))∈L|

G∈Λ(α*SLX×X(F,G))}≤

∨{β∈L|G∈Λ(β)}=ΓΛ(G),

所以

SLX×X(F,G)≤ΓΛ(F)→ΓΛ(G).

根据(LP1)可知,Λ(α),Λ(β)⊆Λ(α∧β),由于

可由完备格上的交运算对任意并是分配的来证得,且由(LUC4)有F∧G∈Λ(α∧β),因此

ΓΛ(F)∧ΓΛ(G)≤

从而(UC4)也是成立的.最后证明(UC5)成立,借助于(LPULIM),当F∘G存在时,(UC5)可由下列式子保证

综上可知,(X,ΓΛ)是L-序一致极限空间.

根据命题2.5和2.6,还可以证明以下推论.

推论2.7对(X,Γ)∈|L-OULIM|和(X,Λ)∈|L-OLULIM|,恒有ΓΛΓ=Γ和ΛΓΛ=Λ成立.

命题2.8设(X,Γ),(Y,Δ)∈|L-OULIM|,φ:X→Y是映射,则φ:(X,Γ)→(Y,Δ)一致连续当且仅当φ:(X,ΛΓ)→(Y,ΛΔ)是一致连续的.

由命题2.5和2.6及其推论2.7,并结合命题2.8可知存在函子η:L-OULIM→L-OLULIM及函子θ:L-OLULIM→L-OULIM,满足等式η∘θ=idL-OLULIM,θ∘η=idL-OULIM.由此得到如下重要的定理.

定理2.9L-序水平一致极限空间范畴与L-序一致极限空间范畴是同构的.

然后,用定理2.9及本文的定理2.2和2.3,可证得L-序水平一致极限空间范畴的如下性质.

推论2.10L-序水平一致极限空间范畴是拓扑的且L是完备Heyting代数时,它是笛卡儿闭的.

最后用下面的定理肯定了L-序水平一致极限空间范畴与L-水平一致极限空间范畴之间的内在联系.

定理2.11L-序水平一致极限空间范畴是L-水平一致极限空间范畴的双反射子范畴.

证明为了用定义1.3证明本定理,任取L-水平一致极限空间(X,Λ).令

EΛ={Λ1|Λ1是X上的L-序水平一致极限

结构且Λ(α)⊆Λ1(α),∀α∈L},

(φ×φ)⟹(F)∈Σ(α)}.

由于对任意α∈L,(φ×φ)⟹(Λ(α))⊆Σ(α),从而有Λ(α)⊆Φ(α).如果可以证明Φ是X上的L-序水平一致极限结构,则Λ*(α)⊆Φ(α)成立,进而有(φ×φ)⟹(Λ*(α))⊆Σ(α),即φ:(X,Λ*)→(Y,Σ)是一致连续的.因此只需证明Φ满足(LUC1)、(LOUC2)、(LUC3)、(LUC4)、(LP1)、(LP2)、(LPULIM)以及(LLC),其中(LP1)和(LP2)是显然成立的.

首先Φ满足(LUC1)是因为Σ满足(LUC1)保证了对x∈X,

(φ×φ)⟹([(x,x)])=[(φ(x),φ(x))]∈Σ(α)

成立.总之,对x∈X,恒有[(x,x)]∈Φ(α),这里α∈L.

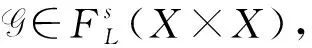
(φ×φ)⟹(G)∈

Σ(α*SLY×Y((φ×φ)⟹(F),(φ×φ)⟹(G))),

再用引理1.2的结论3)有

SLY×Y((φ×φ)⟹(F),(φ×φ)⟹(G))≥

SLX×X(F,G).

这说明对任意α∈L,恒有

(φ×φ)⟹(G)∈Σ(α*SLX×X(F,G)),

即证得G∈Φ(α*SLX×X(F,G)).

第三,Φ满足(LUC3)可由Σ满足(LUC3),然后借助引理1.2的结论1)证得.

第四,为证Φ满足(LUC4),由定义可知对α∈L,F,G∈Φ(α)时,

(φ×φ)⟹(F)∈Σ(α), (φ×φ)⟹(G)∈Σ(α).

如此F∧G∈Φ(α)可由

(φ×φ)⟹(F)∧(φ×φ)⟹(G)=

(φ×φ)⟹(F∧G)

推得.

第五,Φ满足(LPULIM)等价于对F∈Φ(α),G∈Φ(β),且F∘G存在时,F∘G∈Φ(α*β)成立,这里α,β∈L.由引理1.2的结论2)知

(φ×φ)⟹(F)∘(φ×φ)⟹(G)≤

(φ×φ)⟹(F∘G),

故

(φ×φ)⟹(F)∘(φ×φ)⟹(G)∈Σ(α*β)

保证了

(φ×φ)⟹(F∘G)∈Σ(α*β),

这说明F∘G∈Φ(α*β)成立.

最后,为证Φ满足(LLC),任取子集

A⊆{α∈L|F∈Φ(α)}.

由α∈A保证了(φ×φ)⟹(F)∈Σ(α),结合Σ(α)的(LLC)性质可知,(φ×φ)⟹(F)∈Σ(∨A).因此证得F∈Φ(∨A).证毕.

为了清楚L-一致极限空间与L-序一致极限空间的关系,借助定理2.9和2.11,本文有如下推论.

推论2.12L-序一致极限空间范畴是L-一致极限空间范畴的双反射子范畴.