钢轨扣件弹性垫板的动态黏弹塑性力学试验及理论表征研究
韦 凯, 王 丰, 牛澎波, 王绍华, 王 平
(1.西南交通大学高速铁路线路工程教育部重点实验室,四川成都 610031;2. 西南交通大学土木工程学院,四川成都 610031)
钢轨扣件是钢轨与轨枕的中间连接件,对保持钢轨和轨枕的联结、缓解轮轨冲击、减小振动传播起着重要作用。钢轨扣件系统的动力支承性能主要取决于高分子材料弹性垫板。高分子材料的动力行为往往随环境温度、荷载频率非线性变化,同时表现出黏性液体和弹性固体的力学特征,即黏弹性力学特征[1]。此外,钢轨扣件弹性垫板又是含有碳黑等添加剂的复合高分子材料,所以其动力性能还与荷载幅值非线性相关(即类似塑性力学特征的Payne效应)[2]。但是,以往轮轨动力学研究并未重视这一问题,而是简单地将钢轨扣件系统近似视为一个线性弹簧-阻尼系统,比如Kelvin-Voigt(KV)模型等。众所周知,铁路交通跨越温度区域广、轮轨荷载频带宽、振幅变动大且随机性强。因此,线性的KV模型难以准确描述真实服役环境下钢轨扣件弹性垫板随温度、频率、振幅非线性变化的动态黏弹塑性力学行为。为了能够科学地评价钢轨扣件系统的动力支承性能,首先需要准确建立钢轨扣件弹性垫板真实动力服役性能的试验测试与理论表征方法。
钢轨扣件弹性垫板动力性能的试验测试主要包括间接法和直接法两种。间接法基于线性系统的传递函数理论,通过测试系统传递特性来推算弹性垫板动力性能。文献[3-4]构建单向双自由度弹簧-质量系统,通过测试质量块的加速度,间接测试弹性垫板不同激振频率的刚度和阻尼。由于该方法假定系统为线性系统,因此无法测试弹性垫板随振幅非线性变化的情形。直接法通过动力分析仪(DMA)、力学试验机等设备对弹性垫板施加额定激励,直接测试其响应,来估算弹性垫板的动力性能。文献[5-7]通过直接法测试弹性垫板随频率或温度非线性变化的动力性能。与假定线性系统的间接法相比,直接法不仅可以测取弹性垫板随温度或频率非线性变化的动态黏弹性力学性能,还能测量其随动载振幅非线性变化的动态塑性力学性能。
在理论表征方面,最早用于描述高分子材料动力特性的模型是标准机械模型,常用的有KV模型、Maxwell模型、三元件标准固体模型、广义元件模型等。KV模型和Maxwell模型无法同时兼顾刚度和阻尼的频变特性[8],而三元件、广义元件等模型复杂且参数较多[9]。近年随着分数阶微积分理论的发展,分数阶导数黏弹性力学模型因参数少、精度高等优势已开始得到广泛关注。文献[10-14]利用分数导数模型研究黏弹性材料的频变动力性能,在较宽的频率范围内取得了较好的拟合效果,但上述模型只能描述随温度/频率非线性变化的动态黏弹性力学特征。作为改进,文献[15]提出描述高分子材料随动载振幅非线性变化的动态塑性力学模型(Berg摩擦模型),并将其与KV模型并联建立了幅/频变统一模型。文献[16-18]将Berg摩擦模型与分数阶KV模型组合,扩大了幅/频变模型的适用频率范围。但是,分数阶KV模型无法准确描述高分子材料损耗因子随频率(温度)增加(降低)先增大后减小的真实情形,而分数阶Zener模型恰能弥补该缺陷[19]。因此,本文采用分数阶Zener模型与Berg摩擦模型来表征钢轨扣件弹性垫板的动态黏弹塑性力学性能。
首先基于高分子材料的温频等效原理TTS、WLF(Williams-Landel-Ferry)方程与分数阶Zener模型,推导包含温度与频率因子的分数阶Zener模型,通过并联Berg摩擦模型,建立钢轨扣件弹性垫板的动态黏弹塑性力学模型;以我国高速铁路常用的Vossloh300钢轨扣件弹性垫板为研究对象,利用配有温度箱的万能力学试验机(直接法),并应用本文提出的动力学模型(基于TTS和WLF的分数阶Zener模型和Berg摩擦模型)测试与表征该弹性垫板的动态黏弹塑性力学性能,同时讨论预压荷载对其动力性能的影响。期望通过本次研究,提供符合实际的钢轨扣件弹性垫板动力学模型及其参数,以便准确评价真实环境下钢轨扣件弹性垫板的动力服役性能。
1 钢轨扣件弹性垫板的黏弹塑性动力学模型
钢轨扣件弹性垫板的动态黏弹塑性力学行为可由表征温/频变动态黏弹性力学特征的分数阶Zener模型与表征幅变动态塑性力学特征的Berg摩擦模型并联而成,如图1所示。其上部为Berg摩擦模型,下部为分数阶Zener模型。因此,钢轨扣件弹性垫板的合力等于塑性摩擦力Ff与黏弹力Fve(黏性力+弹性力)之和。

图1 钢轨扣件弹性垫板的动态黏弹塑性力学模型
1.1 Berg摩擦力学模型
Berg摩擦模型的数学表达式为[15]

( 1 )
式中:Ffmax为最大摩擦力,kN;x2为0.5Ffmax对应的位移,mm;Ffs和xs为每次位移方向发生变化时参考点的摩擦力(kN)和位移(mm);μ=Ffs/Ffmax,在(-1,1)区间变动。Berg摩擦力与位移速率、试验温度无关,只与当前时刻位移状态有关[15]。
1.2 含温度和频率因子的分数阶Zener模型
经典分数阶Zener模型的时域方程[19-20]为
( 2 )
式中:Fve为黏弹力,kN;K0为激振圆频率ω趋于0时的储能刚度,kN/mm;K∞为激振圆频率ω趋于正无穷时的储能刚度,kN/mm;τ为高聚物松弛时间,s;γ为分数阶数。
通过对式( 2 )进行傅里叶变换,可得到分数阶Zener模型中随频率变化的复刚度

( 3 )
式中:d=K∞/K0。
根据温频等效原理[21],对于密度为ρ0的高分子材料,其在指定频率ω0和指定温度T0下的复刚度可
转换为任意温度T和相关密度ρ下的折算复刚度
( 4 )
式中:α(T)为温度转换因子(温度转换系数),它是温度的函数,与松弛时间有关,可用WLF方程表示[21],求解过程详见文献[22]。

( 5 )
将式( 3 )代入式( 5 )可得任意温度和频率下的复刚度
( 6 )
由式( 6 )可以得到同时包含温度与频率因子的分数阶Zener模型(包括储能刚度、耗能刚度与损耗因子)的表达式为
( 7 )
( 8 )
( 9 )
式中:不同温度下的密度换算方法可参考文献[22],因此K0、d(或K∞)、τ、γ是分数阶Zener模型的4个待定系数。一般情况下,按照定频变温试验(扫温试验)或定温变频试验(扫频试验)的结果来确定这4个待定系数。考虑到温频等效原理的适用性,采用定频变温试验(扫温试验)的结果确定参数时,宜选取弹性垫板玻璃区转化温度之上的测试数据[21]。
2 钢轨扣件弹性垫板的黏弹塑性动力学试验
以我国高速铁路常用的Vossloh300钢轨扣件弹性垫板为研究对象,利用配有温度箱的万能力学试验机对该弹性垫板动力性能进行测试。试验前,在温控箱内按照文献[23]的要求,自上而下依次组装了短钢轨、加载钢板、支承钢板、砂布等配件,如图2所示。

图2 钢轨扣件弹性垫板的试验设备及配件组装
2.1 试验工况
根据钢轨扣件弹性垫板上铁路轮轨荷载的特征分析[13],结合弹性垫板黏弹塑性非线性动态力学特征设计了表1所示的试验工况。其中试验工况5是文献[23]中车辆准静态荷载作用下钢轨扣件弹性垫板动刚度的标准工况,即在20~70 kN范围内的循环加载。该加载过程相当于在预压力45 kN基础上,对弹性垫板进行动载振幅为25 kN的正弦激励。其他试验工况是本文研究拓展的试验工况,用于研究动载振幅与预压力对弹性垫板动力性能的影响。其中,试验工况6~10是相同预压力不同动载振幅的荷载工况,试验工况11~14是相同动载振幅不同预压力的荷载工况。考虑到本试验万能力学试验机的最大安全加载速率不允许超过80 kN/s,因此本试验最大采用30 kN/s的加载速率进行试验加载。

表1 钢轨扣件弹性垫板动力性能的试验工况
另外,由高聚物Mullins效应[24]和Panye效应[2]可知,当荷载幅值较大时,高聚物具有随荷载幅值非线性变化的静态弹性与动态塑性力学特征,将会影响表1试验工况5~14黏弹性动力性能的测试精度。因此,为了准确获取表1中试验工况5~14的黏弹性动力性能,需要预先测取并扣除室温或高温大幅荷载作用下的幅变静态弹性与幅变动态塑性非线性力学性能。这两种非线性力学性能的测试过程类似于文献[23]中车辆准静态荷载作用下钢轨扣件弹性垫板静刚度的测试过程。即在室温20 ℃下完成高于试验荷载的预加载后(该过程能够消除Mullins效应,但仍会存在弹性非线性效应),若以速率近似为0的加载方式从20 kN加载至70 kN(表1中试验工况1),可测得钢轨扣件弹性垫板幅变静态弹性非线性力学性能;类似地,若通过极低加载速率(表1中试验工况2~4)的循环加载方式,可测得钢轨扣件弹性垫板的幅变动态塑性非线性力学性能。
另外,在表1的试验工况5~14中,以5 ℃为间隔,测量定频(0.3 Hz)变温(-60~70 ℃)条件下钢轨扣件弹性垫板的动力性能。已有试验表明我国铁路钢轨扣件弹性垫板普遍具有低温敏感性与高温稳定性,即在20~70 ℃范围内我国多数钢轨扣件弹性垫板的力学参数基本保持不变[22,25]。因此,为节省试验时间,在本试验研究中最高温度仅取至20 ℃。
2.2 试验步骤
在温度箱内完成如图2所示的试验配件组装后,从室温20 ℃开始,以5 ℃为间隔,逐步降至-60 ℃,并在每个温度点至少保温2 h。在保温完成后,首先以3~5 kN/s的加载速率,进行0~100 kN的两次或三次预加载,以消除高聚物Mullins效应;然后以5 kN为间隔,缓慢逐级加载至20 kN,每个加载点变形稳定后,再进行下一级加载;预加载至20 kN并稳定一段时间,以此作为表1每个试验工况的起点。
(1)在室温20 ℃下开展钢轨扣件弹性垫板的幅变静态弹性非线性力学性能测试。在预压力20 kN基础上,以5 kN为间隔,缓慢逐级加载至70 kN。在每级加载后均需保证位移稳定,再进行下一级加载。待加载全部完成后,可得钢轨扣件弹性垫板的非线性弹性力-位移曲线,并用经验公式对其进行理论表征。
(2)仍在室温20 ℃下进行钢轨扣件弹性垫板幅变动态塑性非线性力学性能测试。以预压力20 kN为起点,按照加载频率0.01 Hz对钢轨扣件弹性垫板进行循环加载,可以得到极低频荷载作用下钢轨扣件弹性垫板的动荷载-动位移曲线。若在该滞回曲线中扣除静态弹性非线性力-位移曲线,可以获得钢轨扣件弹性垫板的动态塑性力学滞回曲线,随后应用Berg摩擦模型对其进行理论表征。
(3)在-60~20 ℃(以5 ℃为间隔)的每个温度点上,按照统一的加载频率0.3 Hz,测量相同预压力不同动载振幅与相同动载振幅不同预压力的动荷载-动位移曲线。在钢轨扣件弹性垫板定频变温动荷载-动位移曲线测试完成后,通过扣除(2)中测得的动态塑性力学滞回曲线,可得到定频变温的动态黏弹性力学滞回曲线。应用包含温度与频率因子的分数阶Zener模型,可理论表征钢轨扣件弹性垫板宽温、宽频域的动态黏弹性力学性能。
3 钢轨扣件弹性垫板的黏弹塑性动力学表征
根据以上试验工况与试验步骤,完成高速铁路无砟轨道Vossloh300钢轨扣件弹性垫板动态黏弹塑性力学性能的测试与表征。
3.1 幅变动态塑性力学性能的理论表征3.1.1 幅变静态弹性非线性力学性能
试验得到弹性垫板随荷载幅值非线性变化的静态弹性力-位移曲线如图3所示。从图3可以看出,在大幅静荷载作用下试验弹性垫板位移增量(静刚度)随静荷载幅值的增加非线性递减(递增)。在本试验中,当静荷载从20 kN增至30 kN时,位移增量为0.8 mm(静刚度为12.5 kN/mm);当静荷载从30 kN增至40 kN时,位移增量减至0.5 mm(静刚度增至20.0 kN/mm)。

图3 试验弹性垫板的静态弹性非线性力-位移曲线
试验弹性垫板的静态弹性非线性力学性能可用一个指数形式的经验公式表征
Fne=ax+b[exp(xc)-1]
(10)
式中:Fne为非线性弹性力,kN;x为弹性垫板受压变形位移,mm;a为非线性弹性力-位移曲线的初始刚度,kN/mm;b、c为经验系数。本试验中,a=7.5,b=0.13,c=1.14。
3.1.2 幅变动态塑性非线性力学性能
图4(a)为表1试验工况2~4的动态力学滞回曲线,扣除静态弹性非线性力学曲线后,可得到动态塑性力学滞回曲线,并用Berg摩擦模型对其进行理论表征,如图4(b)所示。


图4 试验弹性胶垫的静态弹性和动态塑性非线性力学曲线
从图4(b)可以看出,Berg摩擦模型能够较好地表征试验弹性垫板随动载振幅非线性变化的动态塑性力学性能。另外,随着动载振幅的增加,滞回环的面积也不断增大,这意味着弹性垫板塑性摩擦阻尼也在增大。在本试验中,试验弹性垫板的Berg摩擦模型系数Ffmax=4.1 kN,x2=0.1 mm。
3.2 温变/频变动态黏弹性力学性能的理论表征
在表1试验工况5~14的定频变温动态力学滞回曲线基础上,通过扣除动态塑性力学性能,获得定频变温动态黏弹性力学滞回曲线,应用包含温度与频率因子的Zener模型,理论表征试验弹性垫板宽温宽频的动态黏弹性力学性能。
3.2.1 定频变温的动态黏弹性力学性能
由于各试验工况定频变温的黏弹性动力性能的获取过程类似,以室温20 ℃下试验工况5为例,介绍试验弹性垫板黏弹性动力参数(储能刚度与损耗因子)的测取过程,如图5所示。

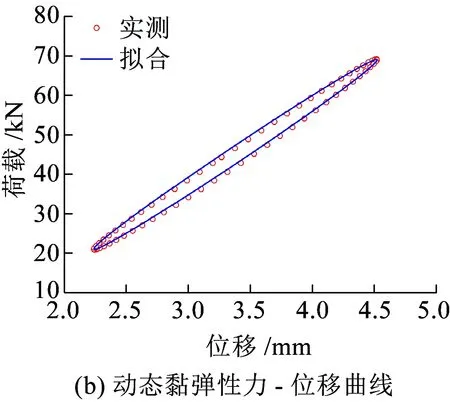
图5 20 ℃时试验弹性垫板动态塑性与动态黏弹性力学曲线
图5(a)显示,即便在较大动载振幅作用下,当动载频率提高(与工况1~4相比)后,试验弹性垫板的动力学滞回曲线基本不受静态弹性非线性的影响,且近似呈椭圆形。另外,扣除动态塑性力学性能后,获得的动态黏弹性力学滞回曲线也近似呈椭圆形。因此,可用线性黏弹性材料的动力学指标对其进行理论表征,即椭圆长轴斜率等于复刚度,荷载与位移相位差的正切值等于损耗因子。试验工况下弹性垫板定频(0.3 Hz)变温(-60~20 ℃)的黏弹性动力学参数(储能刚度与损耗因子)如图6所示。


图6 试验弹性垫板定频(0.3 Hz)变温(-60~20 ℃)下的储能刚度与损耗因子
从图6可以看出,试验弹性垫板的储能刚度随温度的降低逐渐变大,损耗因子则随着温度的降低先增大后减小,并在-45 ℃出现峰值。因此,试验弹性垫板的玻璃化转变温度应在-45 ℃左右。另外,试验弹性垫板的储能刚度、损耗因子与动载振幅基本无关(动载振幅的影响已体现在Berg模型中),但受预压力影响较大,并随预压力增加而增大。在试验工况5中,与室温20 ℃相比,当温度降至-45 ℃时,储能刚度与损耗因子将分别增加了近2.5倍和2.2倍。
3.2.2 宽温宽频的动态黏弹性力学性能
应用基于温频等效原理与WLF方程的分数阶Zener模型(式( 7 )和式( 9 )),通过最小二乘法拟合定频(0.3 Hz)变温(-50~20 ℃)的储能刚度与损耗因子,继而可确定式( 7 )和式( 9 )的4个待定系数。试验工况5的理论拟合效果如图7所示,各试验工况下理论模型的4个待定系数列于表2中。

图7 试验弹性垫板定频(0.3Hz)变温(-50~20 ℃)储能刚度与损耗因子的拟合效果

表2 试验弹性垫板的分数阶Zener模型参数
从图7可以看出,含温度与频率因子的分数阶Zener模型能较好地表征试验弹性垫板的动态黏弹性力学性能。另外,表2显示,在分数阶Zener模型的4个待定系数中,K0和K∞随预压力的增加而增大,而τ和γ基本不受预压力的影响。这说明,钢轨扣件弹性垫板的流变过程基本不受预压荷载的影响,仅与材料性质有关。
获得分数阶Zener模型的待定系数后,便不难得到试验弹性垫板宽温宽频的储能刚度和损耗因子。仍以试验工况5为例,试验弹性垫板宽温宽频的储能刚度与损耗因子如图8所示。图8显示,随着温度的降低,损耗因子最高峰值对应的频率也在减小。在本试验中,室温20 ℃下试验弹性垫板的损耗因子在10 000 Hz附近出现峰值;当温度降至-40 ℃时,损耗因子峰值对应的频率降至10 Hz附近。由于铁路轮轨振动响应的主频带在0.1~10 000 Hz范围内,所以与分数阶KV模型相比,分数阶Zener模型更适合描述低温环境下损耗因子的频变特性。


图8 试验弹性垫板宽温宽频的动态黏弹性力学性能
4 结论
利用配有温度箱的万能力学试验机,应用基于温频等效原理和WLF方程的分数阶Zener模型以及Berg摩擦模型,试验测试并理论表征了我国高速铁路无砟轨道Vossloh300钢轨扣件弹性垫板的动态黏弹塑性力学服役性能。主要研究结论与建议如下:
(1)试验研究表明,当动载振幅较大且频率较低时,钢轨扣件弹性垫板的动力滞回曲线具有随荷载幅值非线性变化的超弹性与塑性力学特征;频率提高之后,钢轨扣件弹性垫板的动态黏弹性力学特征逐渐显现,此时弹性垫板的动力滞回曲线接近线性黏弹材料的动力滞回曲线(近似椭圆形的动力滞回曲线)。
(2)试验结果表明,Vossloh300钢轨扣件弹性垫板随温度/频率非线性变化的黏弹性动力特征与动载振幅基本无关,但随预压力的增加明显增大。另外,Vossloh300钢轨扣件弹性垫板黏弹性动力特征的玻璃化转变温度在-45 ℃左右。
(3)从理论表征效果来看,Berg摩擦模型能较好地描述钢轨扣件弹性垫板随动载振幅非线性变化的动态塑性力学性能。若将其与分数阶Zener模型并联,将能在理论上较全面地表征钢轨扣件弹性垫板的真实动力性能。
(4)基于温频等效原理与WLF方程,推导了包含温度与频率因子的分数阶Zener模型。该模型参数少且使用方便,不仅能快速获得钢轨扣件弹性胶垫任意温度与任意频率下的黏弹性动力特征,且在铁路轮轨振动响应主频带(0.1~10 000 Hz)内更适合描述低温环境下损耗因子的频变特性。

