基于热网络法和有限元法的柔性轴承热分析*

(1.上海大学机电工程与自动化学院 上海 200072；2.宁波慈兴轴承有限公司 浙江宁波 315301)

柔性轴承作为谐波减速的关键零部件，对谐波减速器的传动精度及使用寿命有较大的影响[1]。柔性轴承运动过程中，如果产生的热量不能有效地散发，会引起系统温度升高，导致润滑油黏度下降，润滑状态恶化，导致膜厚减小，引起轴承过早疲劳失效，降低工作效率和使用寿命[2]。因此，研究柔性轴承的发热机制、传热过程及温度分布，对于改善其工作性能有着重要的意义[3-4]。

长期以来，对于普通轴承的发热量和温度场分布计算，一般套用一些经典的计算模型，如HARRIS[5]发热量计算模型和Palmgren发热量计算模型，计算时默认轴承所有零件作为一个整体，每个球的受载一致。而文中以柔性轴承为研究对象，内圈装配有呈椭圆形的波发生器，内外圈发生大变形，每个球的受载、变形、发热量都不一样，因而必须针对每个球的不同情况进行具体计算。

本文作者充分考虑柔性轴承的变形特殊性，首先计算其载荷分布情况，在此基础上，计算柔性轴承发热量和对流换热系数。同时，分别采用热网络法和有限元法进行稳态热分析并进行对比分析，获得柔性轴承温度场分布，研究结果为柔性轴承的设计和后续的优化提供指导[6-7]。

1 柔性轴承的受力分析

文中采用ANSYS有限元数值方法分析得到每个钢球所受载荷。首先建立轴承有限元模型，轴承几何参数和边界条件由表1给出。

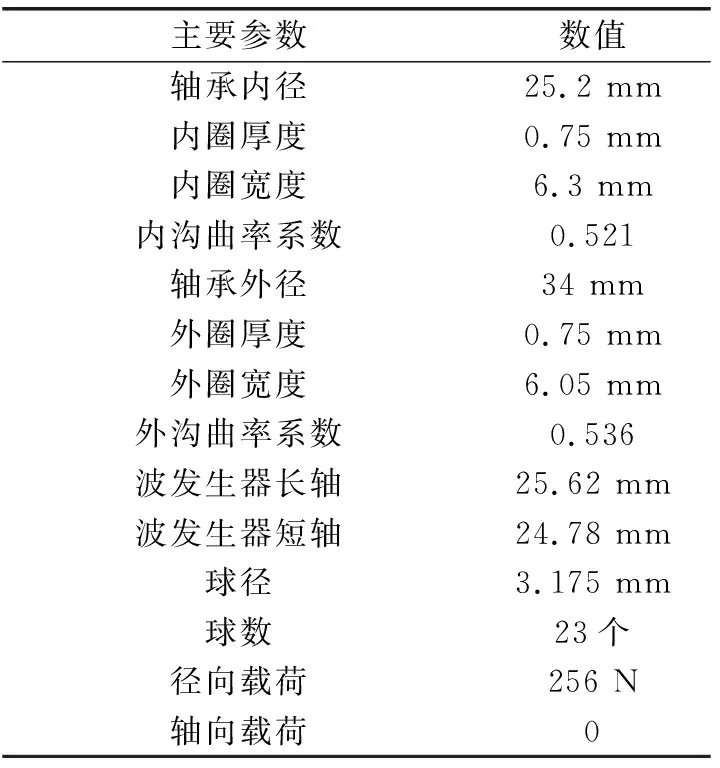
表1 柔性轴承几何参数Table 1 Geometric parameters of flexible bearing

通过ANSYS的建模功能，建立柔性轴承和波发生器的有限元模型，如图1所示。

图1 几何模型Fig 1 Geometric model

为了能够产生谐波，需要在内圈装配一个椭圆形的波发生器，装配前后的变形示意图如图2所示。

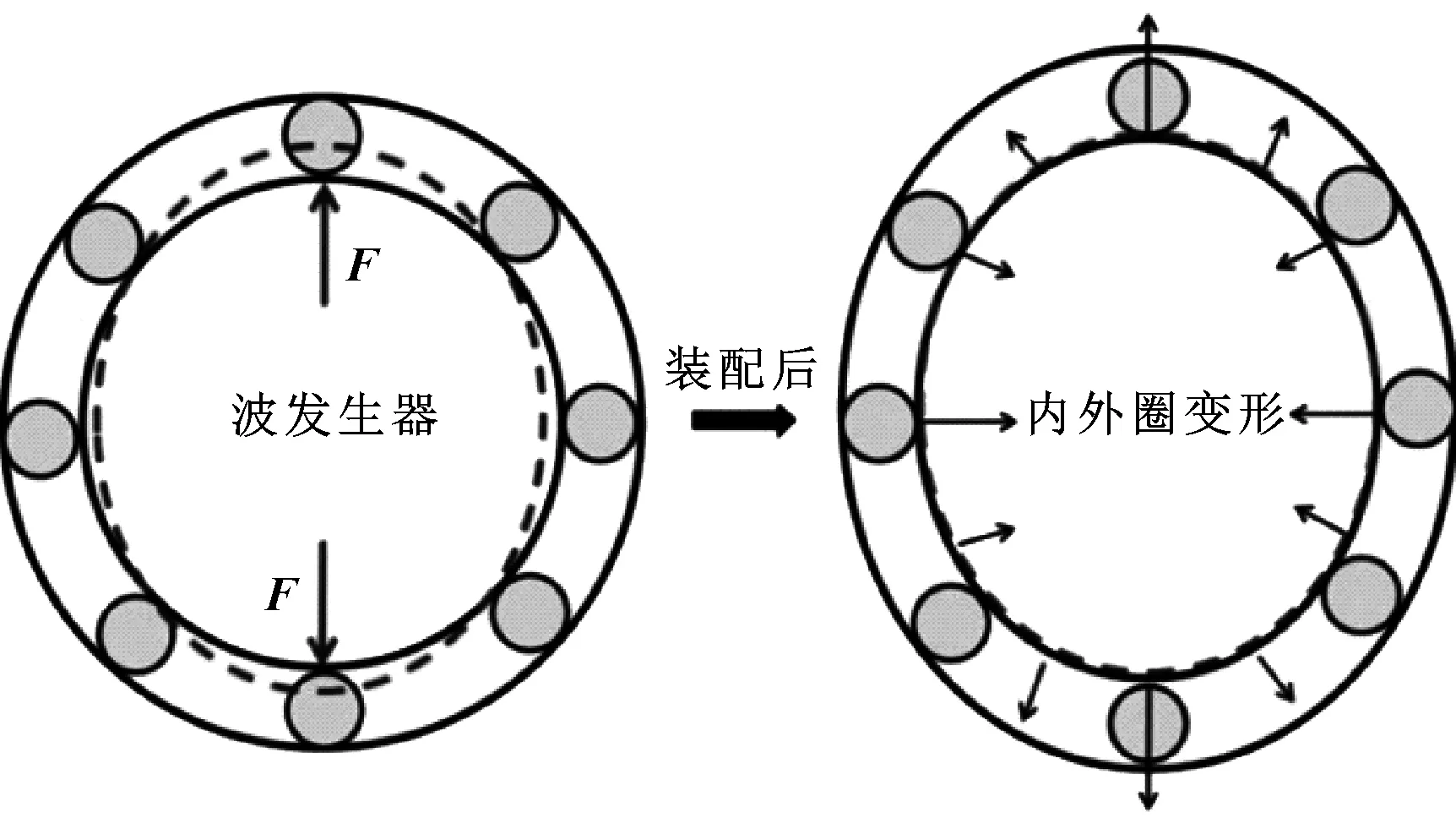
图2 装配示意图Fig 2 Assembly diagram

由图2可知：柔性轴承装配到波发生器时，内圈在长轴附近区域产生过盈，在短轴附近区域产生间隙。

表2 材料属性Table 2 Material properties

设置柔性轴承材料属性和边界条件(如表2所示)，计算后得到柔性轴承的载荷分布。利用ANSYS后处理器技术，将滚动体与滚道的接触反力提取出来，如图3所示。结果表明，23个滚动体中只有13个滚动体承载，且每个滚动体的受载情况不一致，符合实际情况。

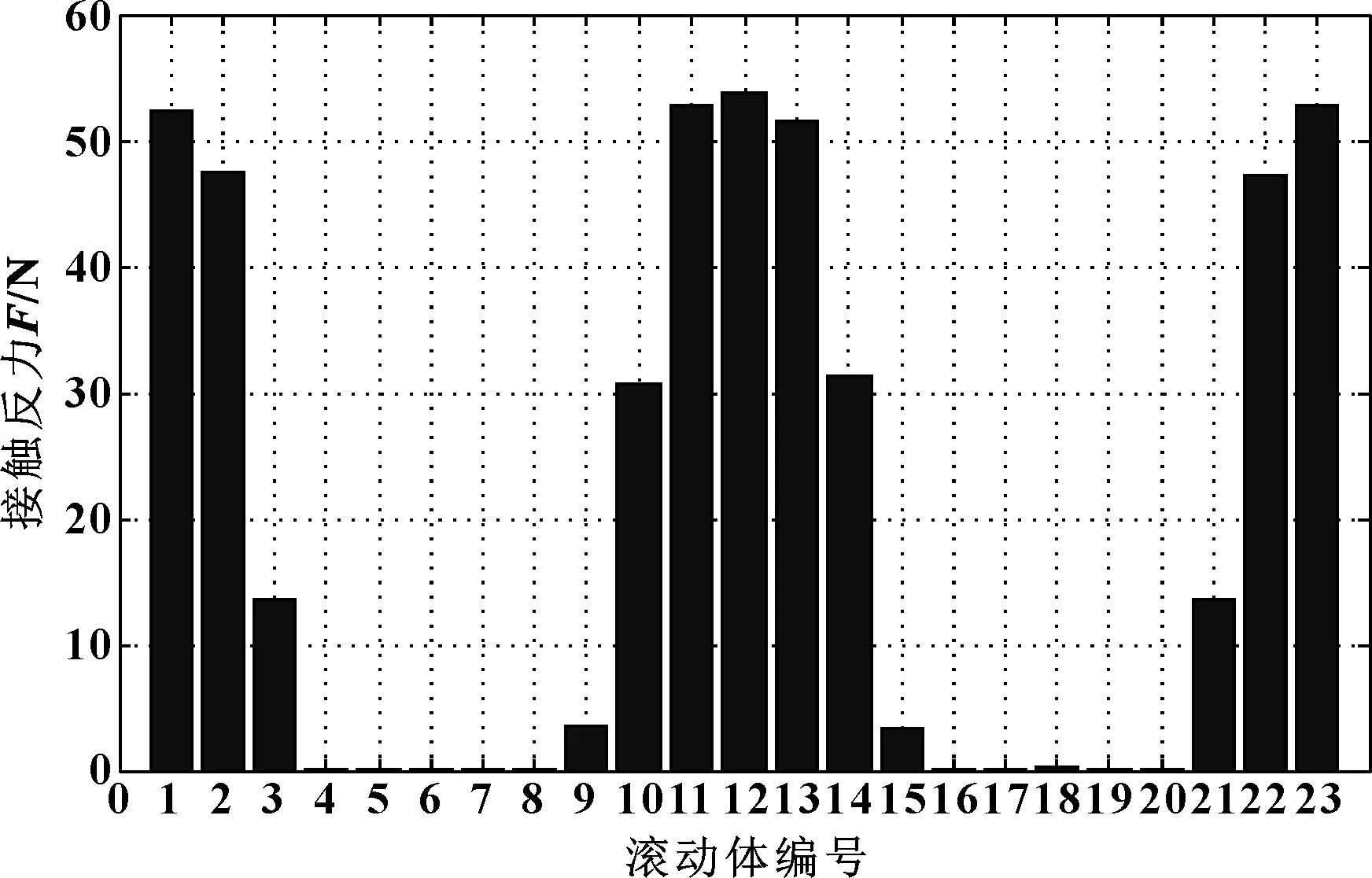
图3 滚动体接触反力Fig 3 Contact reaction of ball rolling

2 柔性轴承发热量计算

柔性轴承的发热主要由其内部的摩擦引起。其摩擦力矩计算文中主要考虑由载荷引起的摩擦及与润滑脂相关的黏滞阻力[8-9]，即：

M=Ml+Mv

(1)

式中：Ml为与柔性轴承的受载相关的摩擦力矩，N·mm；Mv为与柔性轴承润滑相关的摩擦力矩，N·mm。

2.1 载荷引起的摩擦力矩

柔性轴承内外圈由于波发生器的作用将发生大变形，下面分别计算每个钢球因载荷引起的摩擦力矩Mi，然后求和得到总的Ml。公式如下：

(2)

(3)

式中：μ为摩擦因数；dm为节圆直径；n为受载滚动体数；pi为第i个受载荷钢球所承受的力。

2.2 润滑相关的摩擦力矩

柔性轴承在润滑良好情况下，其黏性摩擦力矩根据Palmgren总结的经验公式计算：

式中：f0为与轴承类型及润滑方式有关的系数，文中取为0.7～1.0；n为内圈转速，r/min；ν为润滑脂动力黏度，mm2/s。

最后根据发热量计算公式：H=1.01×10-5Mn得到柔性轴承的总发热量[10]。

3 对流换热系数的计算

经过分析，柔性轴承产生的热量主要以传导、对流及辐射3种方式在零部件之间传递。由于谐波减速器结构紧凑，柔性轴承零部件之间的辐射可以忽略；热传导由材料的属性直接获得；而柔性轴承系统零件表面的对流换热较为重要和复杂，需要准确计算[11]。

文中研究的柔性轴承采用合成脂润滑，因此选择对流换热系数计算模型时，采用计算此类换热较为准确的HARRIS对流换热系数计算公式：

(5)

式中：k为导热系数；Pr为普朗特数，文中取为10；Re为雷诺数，Re=vx/νo，其中νo为润滑脂黏度；x为特征长度，当计算钢球向润滑脂传热时，取x=dm，计算内圈向润滑脂传热时，取x=di，计算外圈向润滑脂传热时，取x=D；v为钢球周向转速。

轴承外表面与空气间的对流换热系数的计算公式为

(6)

(7)

式中：Ta为环境温度；Dh为轴承外圈直径；ka为空气导热系数；v为气流速度，va为空气运动黏度。

4 热网络法

热网络法分析柔性轴承时，将整个系统分解成多个单元体，包括波发生器、内圈、钢球、外圈和柔轮。默认每个单元体内温度均匀，将单元体比拟为热节点，而热节点之间的换热均用热阻代替并联接，形成热网络，并对每个单元或回路利用基尔霍夫定律(KCL、KVL定律)，以温度为待求量建立热平衡方程，从而得到各节点温度[12]。

文中对柔性轴承系统选取9个节点进行分析，其结构模型和热节点分布如图4所示。

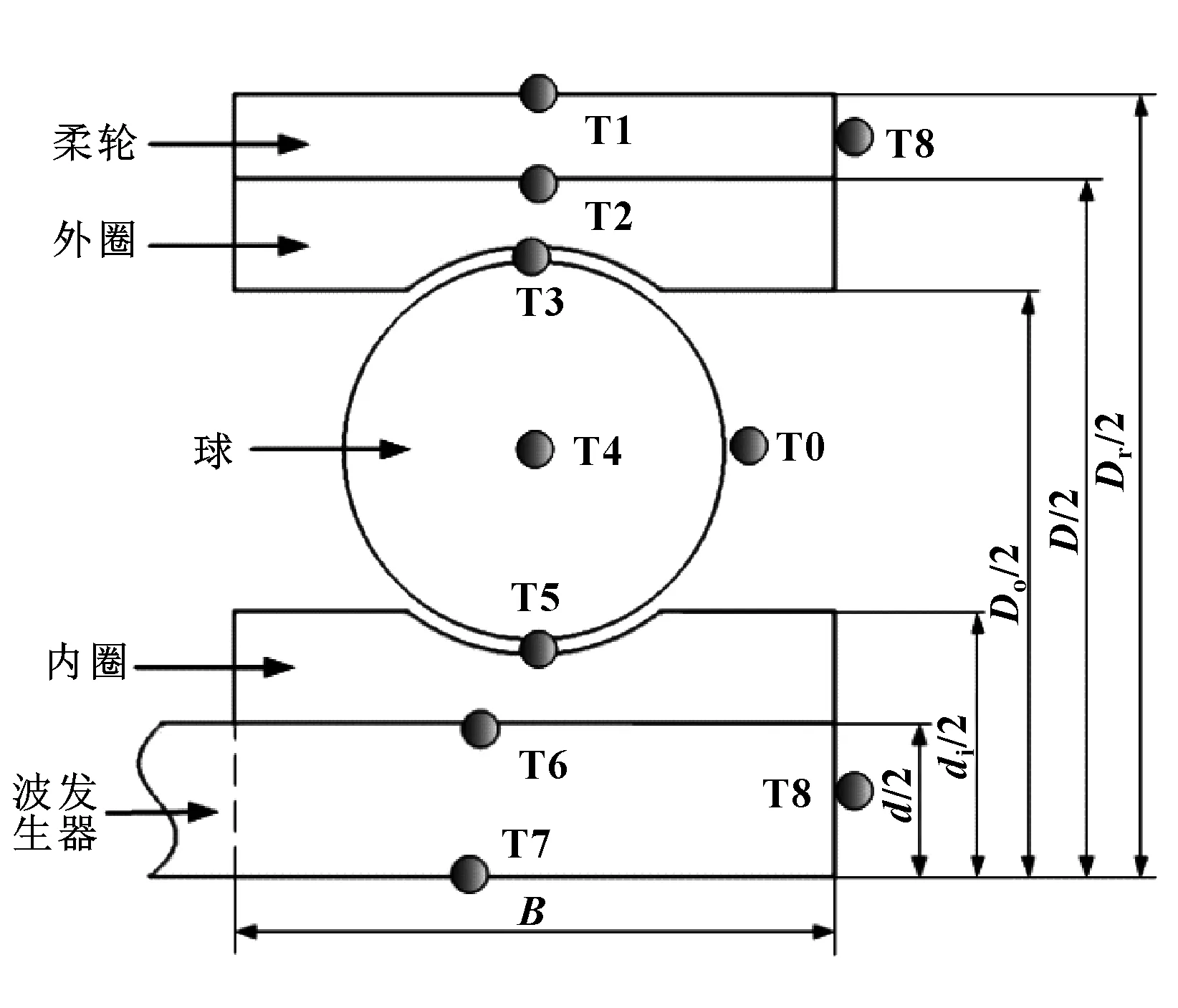
图4 轴承系统结构模型及节点分布图Fig 4 Structure model of bearing system and distribution diagram of heat node

其中，各个热节点对应的位置信息如表3所示。

表3 节点编号位置Table 3 Node numbered position

根据图4所示的热结构图可以建立对应的柔性轴承热网络图，如图5所示。

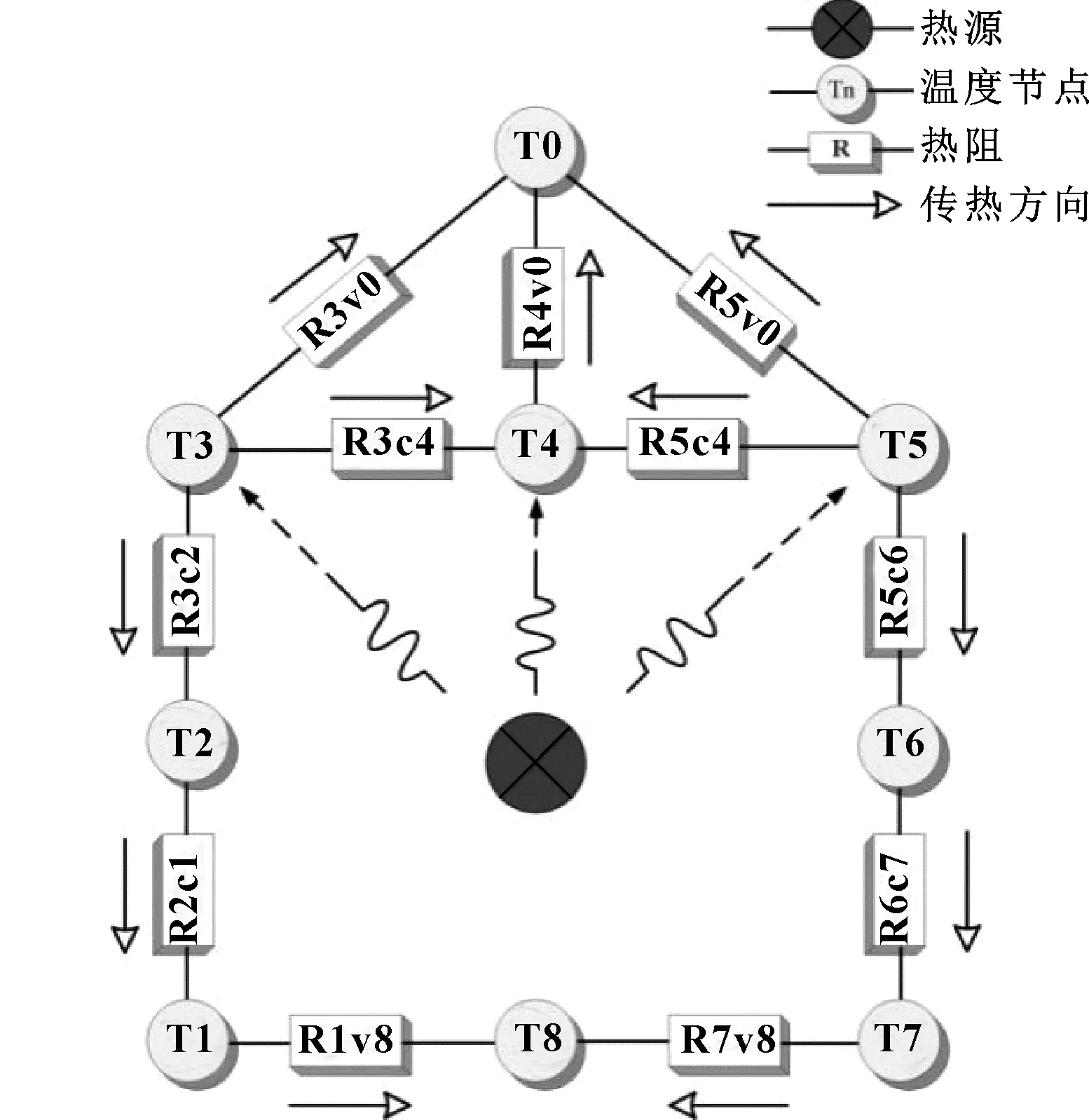
图5 热网络节点Fig 5 Hot network node

依据能量守恒，每个节点中流入、流出的热量相等。因此对柔性轴承系统从T1到T7的7个节点(T0和T8分别为润滑油和空气温度，为已知),即可列出7个热平衡方程，分别为

(1)节点1：(T1-T8)/R1v8+(T1-T2)/R2c1=0

(2)节点2：(T2-T1)/R2c1+(T2-T3)/R3c2=0

(3)节点3：

(T3-T2)/R3c2+(T3-T0)/R3v0+(T3-T4)/R3c4=Q1

(4)节点4：

(T4-T3)/R3c4+(T4-T5)/R5c4+(T4-T0)/R4v0=Q2

(5)节点5：

(T5-T4)/R5c4+(T5-T0)/R5v0+(T5-T6)/R5c6=Q3

(6)节点6：(T6-T5)/R5c6+(T6-T7)/R6c7=0

(7)节点7：(T7-T6)/R6c7+(T7-T8)/R7v8=0

根据傅里叶导热定律和牛顿冷却定律可以计算出相应的导热热阻和对流热阻，计算方法由表4给出。其中，Ravb表示热节点a与b之间的对流换热热阻；Rxcy表示热节点x与y之间的传导热阻；αi、αo、αb、αr、αs分别为轴承内圈、外圈、钢球、柔轮和轴端面的对流换热系数，其值可由对流换热计算公式得到；Kb、Kr、Ks分别是柔性轴承、柔轮和主轴的导热系数，其值由具体材料属性决定[13]。

在采用热网络法进行分析时，通常将摩擦生热的传递比例假设为进入球和进入内外圈各占1/2，因此分别代表外圈、球和内圈生热量的Q1、Q2、Q3可由相应的轴承发热量计算公式得到。

表4 热阻计算公式Table 4 Calculation formula of thermal resistance

最后通过求解方程组得到各热节点的温度。

5 有限元仿真法

5.1 热边界条件的施加

(1)由于钢球与套圈滚道表面接触为主要热源，因此将发热量以热流量的形式施加在内外圈沟道以及球体表面上。

(2)在内外圈以及滚动体的外表面加载对流换热。

最终的热边界施加方案如图6所示。

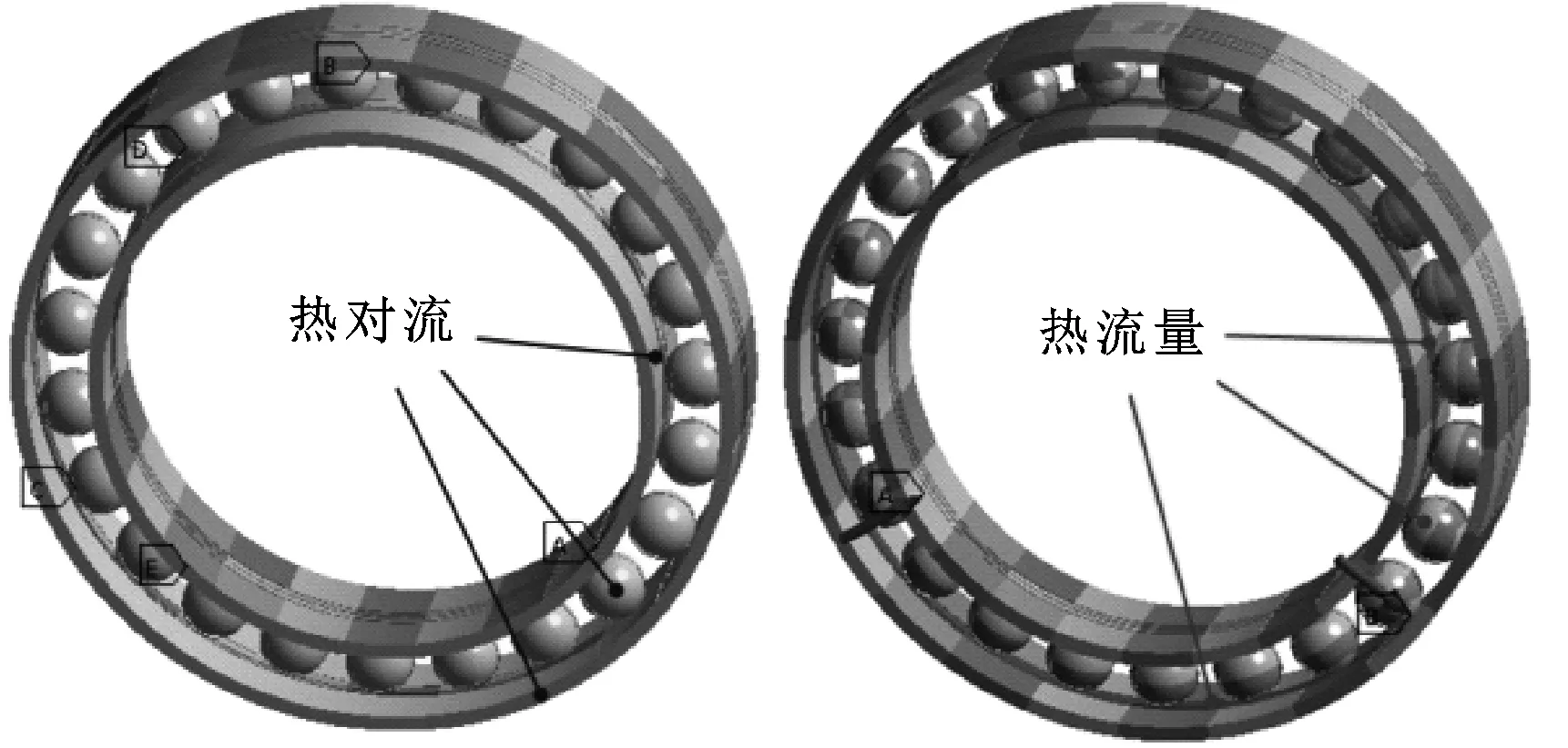
图6 热边界条件施加方案Fig 6 Diagram of thermal boundary conditions

通过上文公式，理论计算得到的柔性轴承发热量及对流换热系数由表5给出。

表5 热载荷计算值Table 5 Thermal boundary condition value

5.2 有限元稳态热分析

通过ANSYS Workbench进行稳态热分析，施加相关热边界条件并进行计算，设置环境温度为22 ℃，得到柔性轴承的温度场分布云图，如图7所示。

图7 柔性轴承整体温度分布Fig 7 Overall temperature distribution of flexible bearings

6 结果分析与对比

由图7可以看出，柔性轴承最高温度出现在滚动体与内圈沟道的接触处，为75.86 ℃，而次高温在内圈表面上，为75.35 ℃，最后沿钢球表面、外圈沟道、外圈表面依次降低。

将有限元计算结果与热网络法计算结果进行对比，结果较为吻合，如表6所示，其误差均在10%以内，为允许工程误差范围，证明了文中有限元及热网络模型具有一定可靠性。

从表6中也可看出有限元法和热网络法的计算结果存在误差，主要因为分析方法的区别，前者为三维分析方法，更接近实际情况，而后者是二维分析方法，在一定程度上做了相应的简化，准确性会有一定有影响。

表6 计算结果对比Table 6 Comparison of calculation results

在有限元法分析中，由于柔性轴承需要发生大变形，为了建模方便和计算更容易收敛，只单独考虑柔性轴承，未将柔轮与波发生器考虑进来，而只是换算成了一定热边界条件内，因此导致热分析中忽略了部分传导热;而热网络法将整个传动系统作为研究对象，分析更全面一些。

7 结论

(1)柔性轴承的整体温度分布具有一定规律，其中最高温度点出现在滚动体与内圈沟道的接触处，而次高温在内圈表面上，最后温度沿滚动体表面、外圈沟道及外圈表面依次降低。

(2)考虑了柔性轴承的特殊性，轴承23个滚动体中，实际受载并产生热量的滚动体个数为13个，弥补了运用普通轴承发热量计算模型的不足，结果更精确，更具有工程实用价值，为柔性轴承的热分析提供了参考依据。

(3)柔性轴承的仿真分析和理论计算是个非常复杂的工程，涉及到的学科非常广，下一步将对其进行相关的试验研究，进一步验证热网络模型及有限元模型计算的可靠性。