空中交通相依网络的脆弱性研究

王兴隆，潘维煌，赵末

1.中国民航大学 空中交通管理学院，天津 300300 2. 空中交通管理系统与技术国家重点实验室，南京 210014 3. 中国民航大学 民航空管研究院，天津 300300

机场、航路和管制扇区是空中交通系统重要组成部分，三者紧密关联、相互依存，任何环节受到扰动，都会影响和传播至其他部分，常常导致航班延误或备降。问题产生根源是机场、航路、管制扇区组成的相依网络存在脆弱性。通过空中交通相依网络脆弱性研究，发现脆弱源及其发生规律，分析运输性能丧失程度，对保障网络正常运行具有重要意义。

作为复杂网络的一部分，相依网络是当下网络研究的热点。国内外相关研究中，Parshani和Buldyrev等[1-2]提出相依网络为两个或以上具有关联关系的网络组成的一个系统，并提出相依网络的脆弱性分析方法；Danziger等[3]对相依网络的节点失效及影响和不同的层网络耦合方式对相依网络的鲁棒性和级联失效作了详细研究；Fu等[4]对互相关联网络的失效传播进行研究，在网络的关联边为不同连接模式下探讨相依网络的脆弱性。相依网络理论应用方面，Laprie等[5]研究了电力关联网络的级联失效进行；Bernstein等[6]分析了电力网络在线路中断时电力荷载转移过程中造成的电力系统的脆弱性；Ouyang[7]研究了基础设施相依网络的层网络间的互相影响。

复杂网络理论在空中交通领域已有一定研究。武喜萍等[8]利用复杂网络研究了空中交通流量网络的静态特性、抗毁性和延误传播模型；徐肖豪和李善梅[9]基于复杂网络理论识别与预测了空中交通拥挤态势。Wang等[10-11]利用复杂网络理论，结合空域结构和航空器几何位置对空中交通的复杂性进行了详细分析；Belkoura等[12]研究了航空网络的拓扑结构，结合网络的结构、动力学特征，从机场、机型、航空公司三方面分析了网络的动态特性，并提出网络结构优化方法。Li等[13]对从拓扑结构和动态过程分析机场网络节点失效后的负载分配规则，研究机场容量与网络性能的关系；Du等[14]利用文化基因算法对中国航路网络的鲁棒性进行分析。Cong等[15]采用聚类算法分析机场网络的关键机场，从机场网络的拓扑结构、网络的时空关联性研究了关键机场与延误之间的联系；Wang等[16]应用元胞自动机对航路网络进行模拟优化，通过调配航路节点的交通流，优化航路网络的容量；Gurtner等[17]分析了欧洲的扇区网络以及特性，并设计了社区发现算法研究扇区网络的生成。Lordan等[18]研究了欧洲航空多层网络结构与鲁棒性之间的关系；Du等[19]利用层网络对中国航空网络进行建模，并讨论了多层航线网络的鲁棒性；Hong和Jiang等[20-22]以各大航空公司的航线网络为层网络，构建航空运输多层网络，计算网络的相关参数分析其网络特性。Voltes-Dorta等[23]构建了以机场为节点，航线为边的航空网络，以全部旅客的总延误分析网络的脆弱性；Han等[24]构建了以导航台节点构建网络，在不同的节点失效模式下研究了导航台网络的脆弱性；Wilkinson等[25]设计相应算法，基于机场的地理空间分析航线网络的脆弱性。

上述相关研究中，建立网络模型往往只关注机场、航路、扇区或航空公司，鲜有考虑网络的相依性；关于空中交通网络脆弱性的研究较少。空中交通网络具有多层性、多属性以及协调性等特点；当目的机场不宜或不能降落时，航班将在备降机场降落。航班备降是空中交通相依网络的脆弱性直接表现。为此，本文构建了空中交通相依网络模型，以结构熵和最大连通度分析网络的结构脆弱性，以交通流量熵和交通流损失比研究网络的功能脆弱性，并给出了求解算法。在随机和蓄意扰动两种失效模式下分析网络结构和功能脆弱性的变化规律。

1 空中交通相依网络模型

空中交通的运行过程是航班由出发机场起飞，空中沿航路飞行，最后在目的机场降落，管制扇区指挥整个过程。本文主要研究空中交通网络脆弱性问题，着重分析在机场失效后交通流的重新分配，当一个机场失效时，航班经常要备降。因此，以机场为节点，机场间备降关系为边构建机场网络G1；以全向信标台、测距台或者无方向性导航台为节点，节点间的航路为边构建航路网，构建航路网络G2；以扇区为节点，扇区间的航班的移交关系为边，将高扇合并到相应低扇中，构建管制扇区网络G3。

采用相依网络的构建方法[26]，通过G1、G2、G3之间交通流的运行关系构建空中交通相依网络，设3个层网络的集合为g={G1,G2,G3}，3对 层网络间依存边的集合为e={E12,E13,E23}，则空中交通相依网络为G0=(g,e)，如图1 所示。

依据空中交通管理规则[27]，建立层网络间的连接方式。机场网络与航路网络的依存边E12为机场节点与相应航路网络节点的连接，表示航班由机场进入航路或者由航路降落机场连接关系。机场网络与管制扇区网络的依存边E13为机场节点与相应管制扇区网络节点的连接，表示管制扇区对相应机场航班起降的指挥。航路网络与管制扇区网络的依存边E23为航路节点与相应管制扇区网络节点的连接，表示管制扇区对航路交通流的指挥与控制。E12、E13和E23均为加权、有向的连接，权重为连边的交通量。特别地，航路节点和管制扇区节点正常工作下相应的机场节点才能实现航班起降功能；管制扇区节点正常工作下相应的航路节点才能实现航班运输功能。通过分析该模型在扰动下的网络性能变化，研究实际空中交通系统脆弱性规律。

图1 空中交通相依网络模型Fig.1 Model for air traffic interdependent network

2 空中交通相依网络脆弱性分析

脆弱性是系统的固有属性[28]。空中交通相依网络自身存在一定缺陷或薄弱环节，若受到外界的扰动，则引起网络的某些节点的功能部分或完全失效，影响网络运行。同时失效的节点也会在网络中传播和扩散，引起更大范围的节点失效。若网络的脆弱性是源于网络自身的拓扑结构，称为网络结构脆弱性；在交通流运行时，由于受到扰动才引发的脆弱性，称为网络功能脆弱性。本文将扰动分为蓄意扰动和随机扰动，其中，蓄意扰动是网络节点按一定策略被删掉，随机扰动是网络节点按概率被随机删除。

2.1 网络结构脆弱性分析

2.1.1 结构脆弱性评价指标

空中交通相依网络具有有序和无序两种状态，有序是指网络结构稳定，航班按时起飞、降落，交通流运行平稳；无序是指网络结构不稳定，航班运行出现排队、备降和大范围延误，存在风险隐患。熵是描述复杂网络状态的一个重要参数，其量值变化可确切地表示网络状态的变化，熵值增加表明网络从有序状态向无序状态变动，熵值减则反映网络从无序向有序变动。

定义1网络结构熵：描述由节点分布差异性形成的网络结构特性，根据熵值变化分析空中交通相依网络节点脆弱性。结构熵计算公式为

(1)

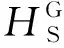
(2)

式中:Ki为网络中节点i的度。

由式(1)可知，当网络中所有节点的度均不一致时，网络结构熵最大；所有节点的度均相同时，网络结构熵最小。为了分析不同层网络的结构熵，进行归一化处理：

(3)

定义2最大连通度：网络的节点被扰动后，可能造成其他节点的孤立，孤立节点会被去除。此时，网络中仍与最大子图相连的节点数目与节点总数的比值就是最大连通度，计算公式为

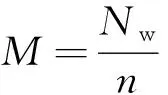
(4)

式中:M为网络的最大连通度；Nw为在节点扰动后网络中仍与最大子图相连的节点数目。

利用最大连通度的大小研究网络的脆弱性，根据层网络在不同扰动模式下的最大连通度的下降率进行分析，相同的节点失效比例下M值下降越快，网络脆弱性越显著。

2.1.2 结构脆弱性分析方法

由空中交通管理规则和各层网络的逻辑连接关系，建立层网络节点失效的影响方式：

1) 机场节点失效，并不会导致管制扇区网络和航路网络节点失效。

2) 航路节点失效，与失效节点相连的机场节点也失效，与之相连的管制扇区网络节点不失效。

3) 管制扇区节点失效，与失效节点相连的航路网络节点、机场网络节点均失效。

4) 节点失效后网络若被分为若干个连通子图，不在网络中最大连通子图内的节点也失效，这些失效节点按上述规则影响其他层网络的节点。

在随机和蓄意两种扰动模式下，计算不同比例失效节点的结构熵和最大连通度的大小。若某一层网络完全失效或者节点扰动比例达到50%，终止计算。设计网络结构脆弱性算法，其计算步骤如图2所示。

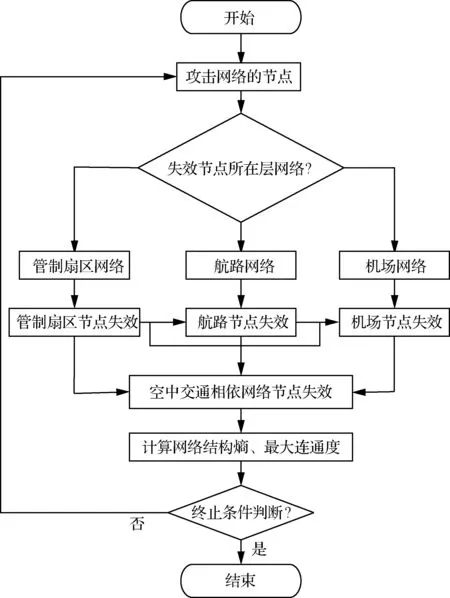
图2 结构脆弱性算法Fig.2 Algorithm of structural vulnerability

2.2 网络功能脆弱性分析

2.2.1 功能脆弱性评价指标

定义3流量熵：网络中交通流在节点失效后需要重新分配，在交通流的重新分配的过程中，网络处于一种脆弱性易发的状态，流量熵可以刻画这种状态。其计算公式为

(5)

(6)

式中：ti为节点i的交通量。

为分析不同层网络间的流量熵，进行归一化处理：

(7)

定义4交通流损失比：网络中的节点被去除到一定的水平后，剩余节点将无法承接交通流的转移，无法承接的转移流量与去除节点交通流总量的比值，就是交通流损失比，计算公式为

(8)

式中：l为网络的交通流损失比；t(q)为q比例的节点遭到去除后，网络无法承接的交通量；T(q)为被去q比例除节点交通量的总和。

由式(8)可知，l越接近1，网络无法承接的交通量越接近去除节点交通量的总和，此时网络交通量接近饱和，网络功能脆弱性越明显。

2.2.2 网络功能脆弱性分析方法

研究空中交通相依网络功能脆弱性，首先分析节点被扰动后交通流转移规则与流程，分为层网络间和层网络内，具体流程如下：

1) 层网络间的交通流转移

机场节点失效，相连的管制扇区节点和航路节点不发生交通流转移。

航路节点失效，相连的机场节点发生交通流转移。

管制扇区节点失效，相连的机场节点和航路节点均需要进行交通流转移。

2) 层网络内的交通流转移流程

机场节点失效，其交通流将被转移至相邻机场节点。

航路节点失效，其交通流将被转移至相邻航路节点。交通流转移受相连的管制扇区节点的裕度约束，若转移量超过扇区节点的裕度，则以扇区节点裕度作为交通流转移最大量。

管制扇区节点失效，其交通流将被转移至相邻扇区节点。交通流转移受相连的航路节点的最大裕度约束，若转移量超过航路节点的裕度，则以航路节点裕度作为交通流转移最大量。

失效节点i转移至相邻节点j的交通量tij为

(9)

式中：ti为失效节点i的交通量；U为节点i相邻节点的集合，j∈U；Yj为节点j的裕度，Yj的计算公式为

Yj=cj-tj

(10)

式中：cj为节点j的容量；tj为节点j的交通量。

在网络交通流转移完成后，计算网络流量熵和交通流损失比。若空中交通相依网络中某一层网络完全失效或者节点扰动比例达到50%，终止计算。设计网络功能脆弱性算法，其计算步骤如图3所示。

在图3中：Yaj为机场网络节点裕度；Yhj为航路网络节点裕度；Ygj为管制扇区网络节点裕度。

图3 功能脆弱性算法Fig.3 Algorithm of functional vulnerability

3 算例分析

本文采集民航华北地区的实际数据，构建华北空中交通相依网络，分析网络结构脆弱性和功能脆弱性。

3.1 华北空中交通相依网络

华北地区共计28个机场，具有备降关系的机场共计79对，机场网络如图4(a)所示；华北地区共计41个导航点，90条航路，航路网络如图4(b)所示；华北地区共计20个管制扇区，43条边。管制扇区网络如图4(c)所示。华北空中交通相依网络的构建方法见图1。

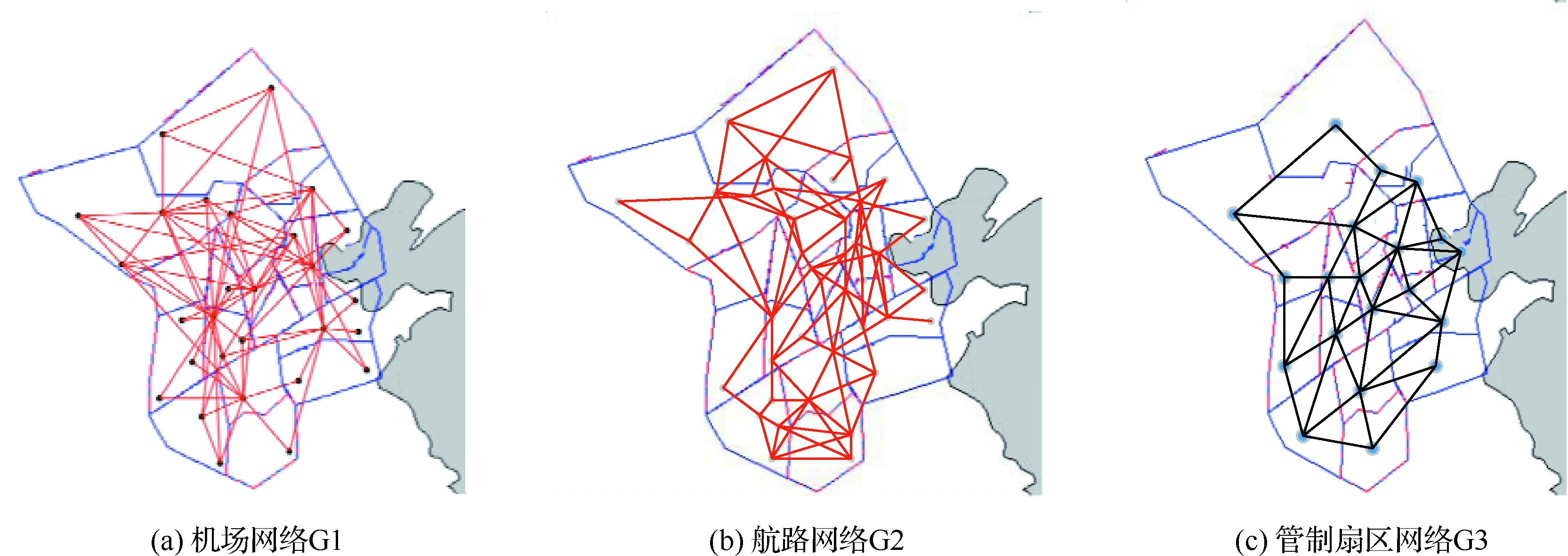
图4 华北相依网络模型Fig.4 Model for North China interdependent network

3.2 网络结构脆弱性分析

对华北空中交通相依网络的节点进行随机和蓄意扰动，其中，蓄意扰动是根据节点在层网络中的度值大小依次扰动，当度值相同时随机选取节点进行扰动。分析扰动后相依网络的结构熵和最大连通度的变化趋势，探索网络的脆弱源及其产生原因。

1) 网络结构熵。由式(3)的指标和图2的算法步骤，计算华北空中交通相依网络的结构熵，结果见图5。

图5中：R表示随机扰动；D表示蓄意扰动；G0表示空中交通相依网络；R,Gx,Gy表示对Gx的节点进行随机扰动，Gy的指标变化。x，y∈{0，1，2，3}。

若网络结构脆弱性没有被触发，结构熵会随着节点失效的比例增加而下降。若结构熵并未随着节点失效而下降，反而维持在一个较高的值，表明结构脆弱性显著。

① 扰动G1在随机扰动下，G1、G0结构熵值分别在0.46～0.73、0.48～0.52的范围内，其间出现熵增现象，向无序变动的趋势明显；在蓄意扰动下，G0熵值在0.48～0.52的范围内，出现熵值现象为无序状态；G1熵值逐渐减少，网络有序。

② 扰动G2在随机扰动下，G2、G1、G0结构熵值出现熵增，整体表现为无序；在蓄意扰动下，G1、G2熵值在0～0.68、0～0.52内递减，表现为有序；G0熵值在0.39～0.52范围内，出现熵增现象，表现为无序。

③ 扰动G3在随机扰动下，G0、G1、G2、G3结构熵值均在0.39～0.79范围波动，出现熵增现象，网络变得无序；在蓄意扰动下，G0、G1、G2熵值前期下降，后期维持在某个值，无熵增现象，G3值缓慢下降，此时网络整体表现为有序。

图5 网络结构熵Fig.5 Structure entropy of network

分析发现网络结构熵值有突然增加的情况，一方面是因为节点的扰动产生了级联失效，失效不断累积并通过网络的传播影响至网络的更多节点；另一方面是扰动的节点有可能是节点度值较大的节点，导致网络中节点度分布差异过大而使得网络结构熵增加。

2) 网络最大连通度。由式(4)与图2节点失效转移算法，在不同扰动模式下计算网络的最大连通度M，结果见图6，图例含义同图5。

① 扰动G1。无论随机还是蓄意扰动下，G1的M值下降快， G0下降最慢，说明G1结构被扰动影响较大，G0被影响较小。

② 扰动G2。在随机扰动下，G0、 G1、G2的M值下降依次加快，结构被破坏的程度依次加深；在蓄意扰动下，G0、 G2、G1的M值下降依次加快，结构被破坏的程度依次加深；蓄意扰动破坏作用强于随机扰动。

③ 扰动G3。在随机扰动下，G3、 G0、G2、G1的M值下降依次加快，结构被破坏的程度依次加深；在蓄意扰动下，G3、G2、G0、G1的M值下降依次加快，结构被破坏的程度依次加深。

综上结构熵和最大连通度分析可知，网络结构脆弱性主要源于G1和G3。

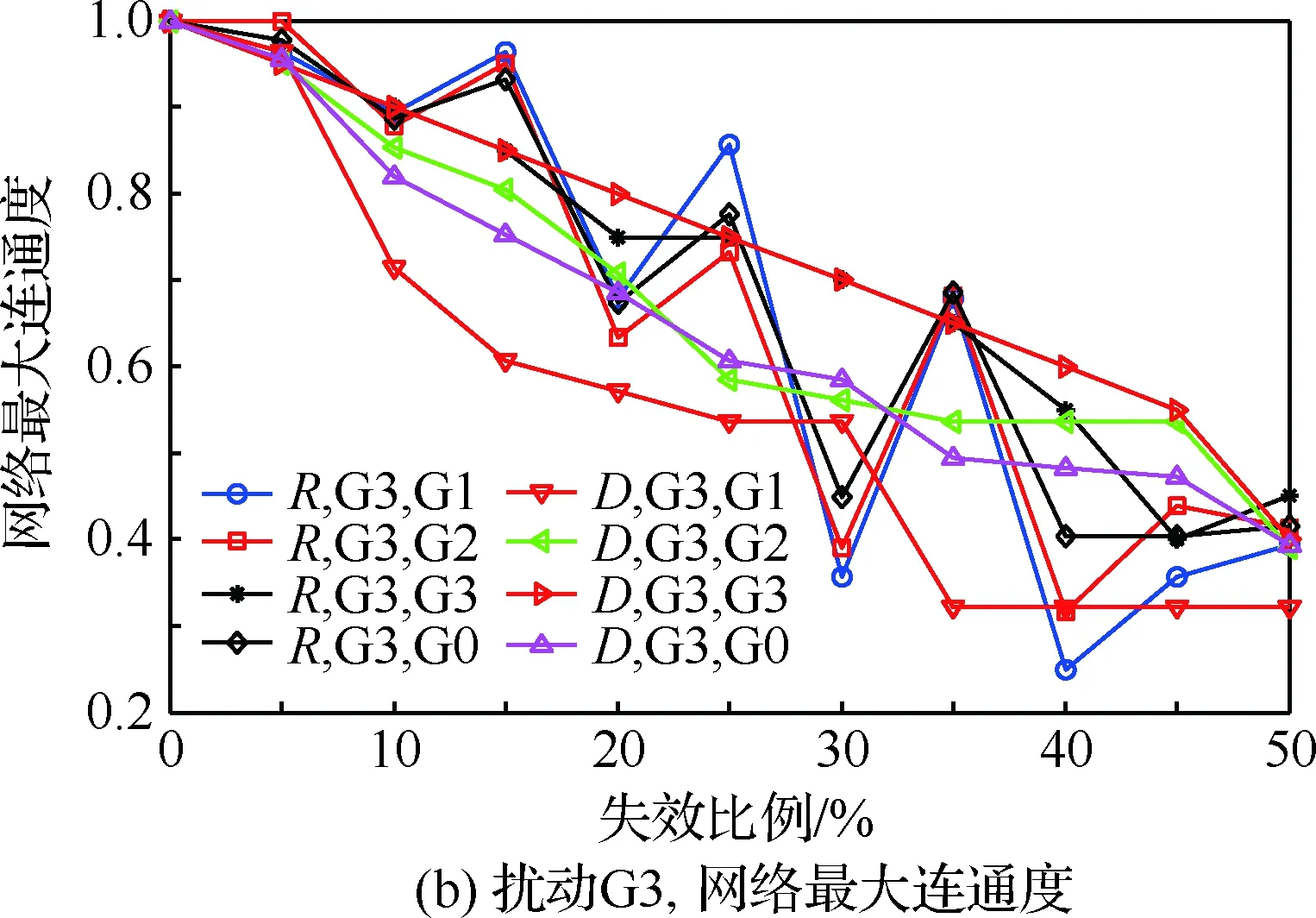
图6 网络最大连通度Fig.6 Maximum connectivity of network

3.3 网络功能脆弱性分析

分析功能脆弱性时，蓄意扰动是根据节点在层网络中的交通流量大小依次进行扰动。在随机和蓄意扰动后，分析网络流量熵和交通流损失比变化规律与原因。采集民航华北地区雷达航迹数据，通过TrackDig软件平台统计的机场、航路和管制扇区的流量数据。

1) 网络交通流量熵。由式(7)和图3节点失效的交通量转移流程，计算华北空中交通层网络的流量熵，结果如图7所示。R, Gx表示对Gx层网络的节点进行随机扰动，相应纵轴坐标指标的变化。

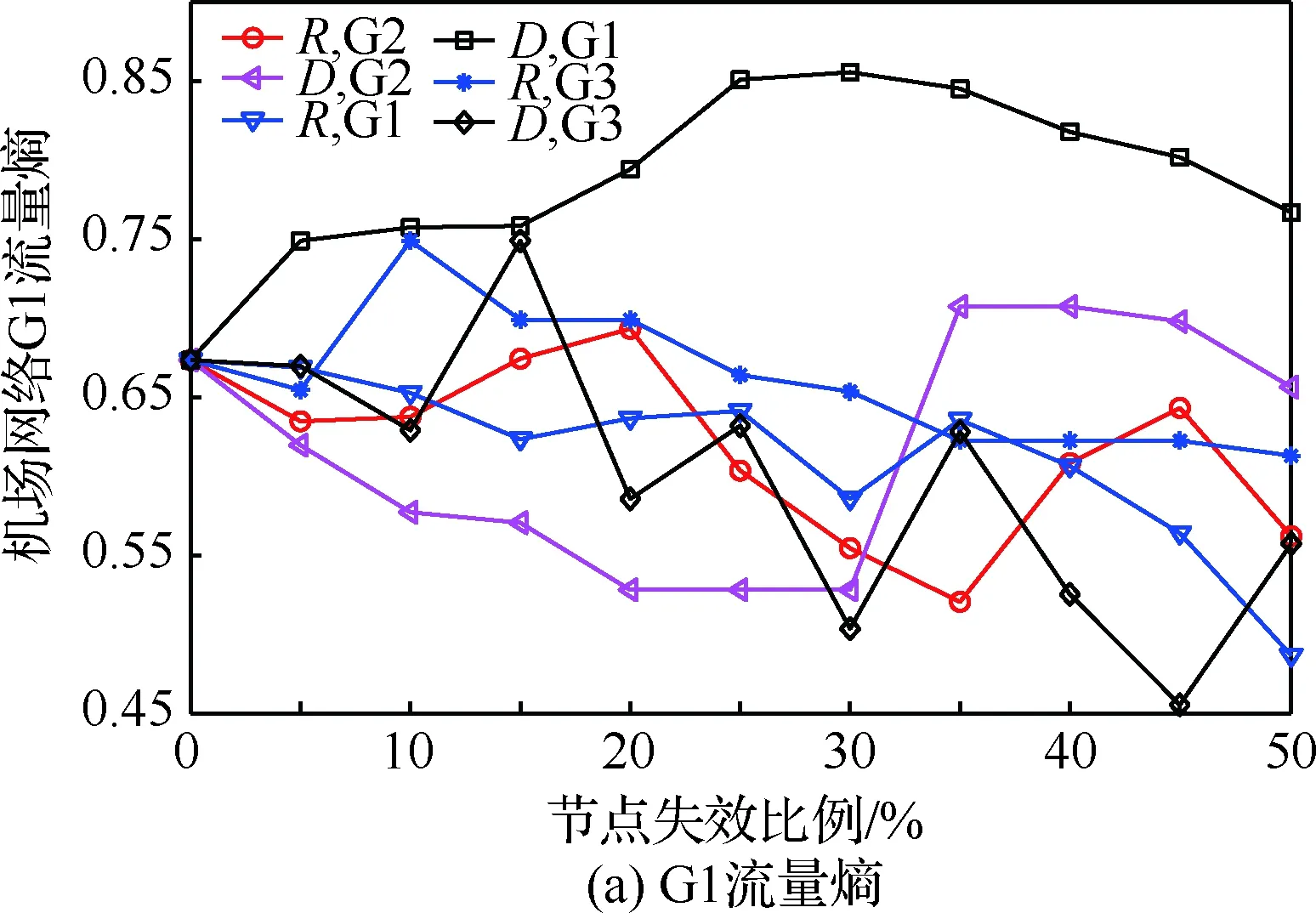
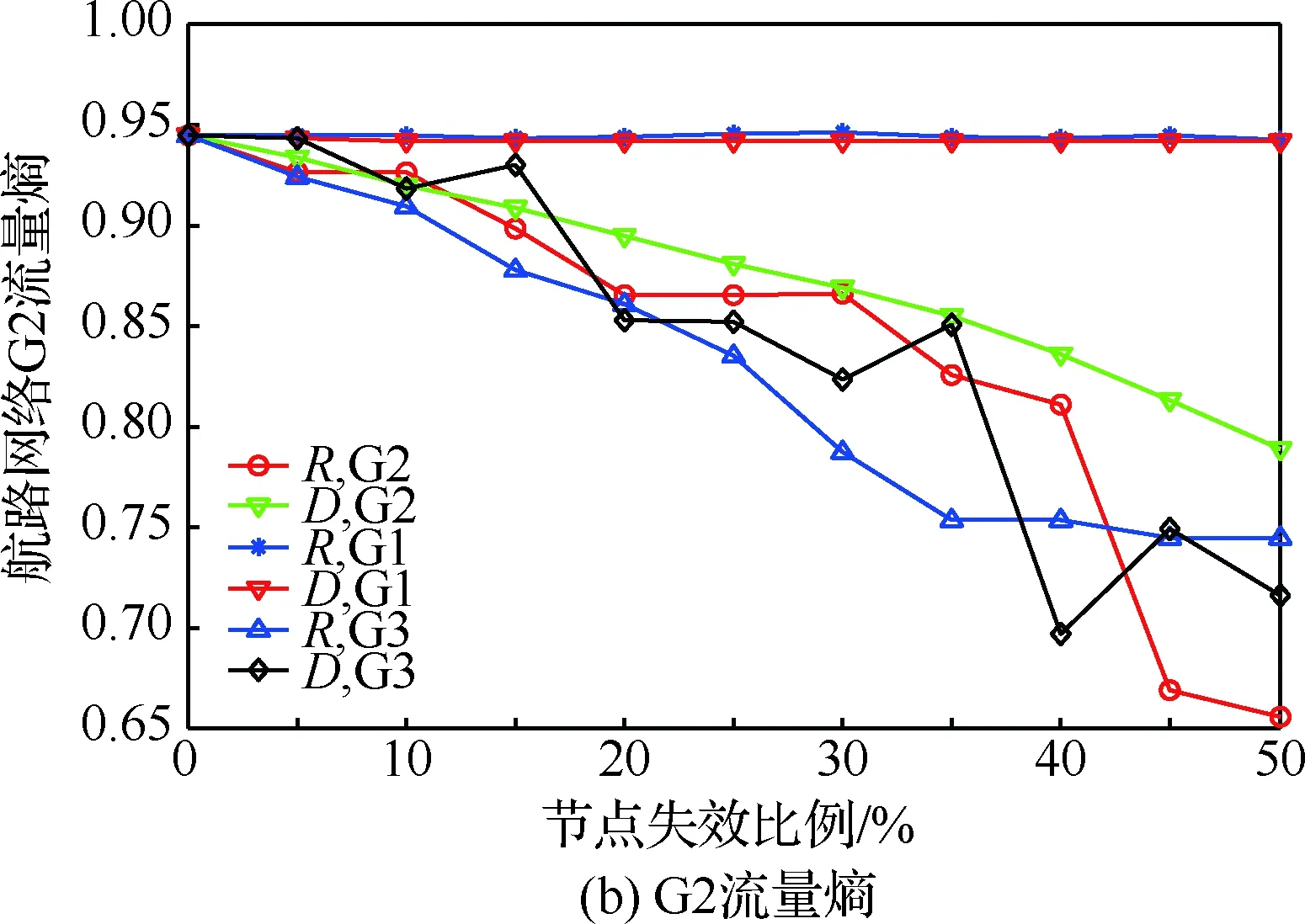
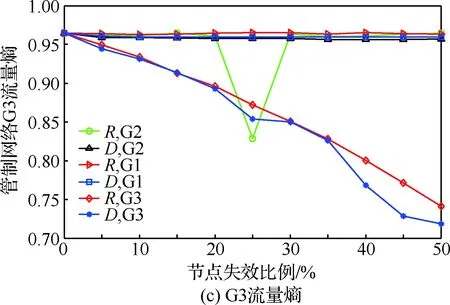
图7 网络交通流量熵Fig.7 Traffic flow entropy of network

① G1流量熵。随机或蓄意扰动G1、G2和G3，流量熵值都出现明显的增加，即G1在所有的扰动下都为无序变动。

② G2流量熵。随机或蓄意扰动G1，G2的流量熵在0.93～0.94波动，处于无序状态；蓄意扰动G3，G2出现熵增现象，网络仍处于无序状态；随机扰动G3，随机或蓄意扰动G2，流量熵逐渐减少，没有出现熵增，此时G2处于有序状态。

③ G3流量熵。随机或蓄意扰动G3，流量熵值减少，网络处于有序状态，随机或蓄意扰动G1、G2，流量熵值大部分在0.955～0.965范围波动，网络处于无序状态。

分析发现流量熵值有突然增加的情形。原因一方面是节点扰动使得流量在转移过程中也产生了级联失效，使得更多的节点因过载而失效，使得网络的流量分配更加不均衡而造成熵增；另一方面也可能由于扰动的节点可能自身流量较大，流量转移后网络的流量变得更不均衡而引起的熵增。

2) 网络交通流损失比。由式(8)和图3节点失效的交通量转移算法，计算网络交通流损失比，结果如图8所示。

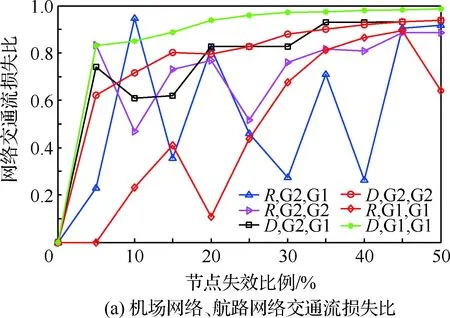
图8 网络交通流损失比Fig.8 Traffic flow loss ratio of network

① 扰动G1。在随机扰动下，G1的L值上升最慢；在蓄意扰动下，G1的L值上升最快，说明蓄意对G1进行扰动造成较大的交通流损失。

② 扰动G2。在随机扰动下，G1的L值上升最快，G2的L值上升较快，在蓄意扰动下，G1、G2的L值上升幅度均较大。随机扰动G2，G1比G2的交通流损失更大；蓄意扰动G2，G1、G2的交通流损失均较大。

③ 扰动G3。在随机扰动下， G1的L值上升幅度最大，G2、G3的L值上升幅度较大；在蓄意扰动下，G1的L值上升幅度最大，G2、G3的L值上升幅度较大。扰动G3，G1交通流损失最大，G2、G3交通流损失较大，但蓄意扰动下各网络交通流损失更多。

综上功能脆弱性分析，G1在扰动下总是表现出无序。蓄意扰动较小比例的节点造成网络的交通流损失比迅速达到一个较高水平，说明层网络的交通流在荷载转移过程中难以得到匹配，因节点失效而需要转移的交通流受到相连的层网络的交通量的制约，网络的功能脆弱性因此而表现出来。

通过华北空中交通相依网络脆弱性分析，保障G1通畅运行，协调G1、G2、G3层网络间的流量可以减少航班延误和备降，提高网络运输性能，有效降低华北空中交通相依网络的脆弱性。

4 结 论

1) 建立的相依网络模型，客观表示出空中交通实际运行过程，反映机场、航路和管制扇区相互耦合关系，有利于分析网络特征。

2) 空中交通相依网络脆弱性指标充分考虑了静态结构和动态流量因素，采用随机和蓄意两种扰动方式分析，结果显示随机扰动节点对空中交通相依网络的脆弱性影响更大，在机场、航路和管制扇区3个层网络中，机场网络在受到扰动时脆弱性最明显。

3) 空中交通相依网络的逻辑连接方式与层网络间的交通流量不匹配是空中交通相依网络脆弱性的主要原因。

4) 针对机场、航路和管制扇区运行时相依、扰动时脆弱性的特征，提出的研究方法有助于提高流量管理策略有效性，减少航班延误和备降。

由本文分析可知，空中交通网络脆弱性不仅影响运行效率，也会产生重大风险隐患，因此深入分析脆弱性产生机理并建立有效的保护策略，是需要进一步研究的问题。