液体火箭发动机三轴向虚拟振动试验技术研究
韩 帅,曹亚文,邓长华,穆朋刚,霍世慧,李斌潮,薛 杰
(西安航天动力研究所,陕西 西安710100)
0 引言
振动试验是液体火箭发动机结构可靠性评估和力学环境适应性验证的重要内容[1-3]。通常情况下采用单轴振动台依次进行结构三个互相垂直方向的试验来模拟产品所处的实际振动环境,但有时单轴振动试验无法激发出结构的真实故障模式。相比于单轴振动试验,三轴向振动试验能够更加真实地模拟产品的实际受力状态。目前三轴向振动台越来越多的被应用于模拟结构实际所处的振动环境研究中,但单轴振动试验与三轴向振动试验之间有着怎样的区别与联系,以及如何对单轴向振动试验的输入谱进行修改以应用于三轴向振动试验等问题目前还没有成熟的方法。基于此,开展三轴向虚拟振动试验研究,对于分析结构在单轴向和三轴向振动试验中的动态响应区别,以及研究修改单轴向振动试验输入谱以适用于三轴向振动试验都具有重要的研究价值。
关于虚拟振动台试验技术的研究目前主要有两种途径:一种是采用振动台机电耦合模型与振动台多刚体动力学模型相结合的方法构建振动台计算模型;另一种是对振动台直接进行有限元建模,通过与产品进行联合仿真建模的方式进行虚拟振动试验。本文采用有限元方法构建了三轴向振动台动力学仿真模型,开展了三轴向振动台虚拟振动试验系统设计和控制方法的研究工作。对某试件分别进行了x,y,z轴向一维虚拟振动试验以及三维虚拟振动试验,并对一维和三维虚拟正弦振动试验结果和虚拟随机振动试验结果进行了对比分析。
1 电动振动台工作原理
电动振动台工作原理是基于载流导体在磁场中受到电磁力作用的安培定律[4-5]。电动振动台台体内有两组励磁线圈,一组在中间板上侧,一组在中间板下侧。当直流电流通过励磁线圈,会在励磁线圈周围产生磁通。上下励磁线圈的磁通在动圈处形成一个高磁感应强度的环形气隙,当经过功率放大器放大的交变电流信号通过动子线圈时,根据安培定律,会在励磁磁场的作用下产生交变力F,使动圈沿图示运动方向上下运动。设电流简谐变化,i=Isinωt,则力F=Bli=BlIsinωt,其中B为励磁磁场的磁感应强度;l为动子线圈绕线的有效长度;I为动圈中的电流。
2 三轴向电动振动台建模技术
三轴向虚拟振动建模技术包括三轴向电动振动台有限元建模和三轴向虚拟正弦、随机振动控制方法研究[6-9]。
2.1 三轴向电动振动台有限元建模
以某10T三轴向电动振动台为研究对象进行建模。振动台几何模型直接采用CAD软件进行建立。在UG中建立三轴向电动振动台各部件(台体、静圈、动圈、牛头、平动式静压导轨连接器、中心悬浮体及扩展台面等)几何模型[10-12]如图1所示。

图1 三轴向振动台几何模型Fig.1 Geometrical model of three-axial vibration test bench
将三轴向振动台各个部件的CAD模型导入MSC.Patran软件环境下建立相应部件的几何模型及有限元模型。其中,可动部分包括动圈、牛头、平动式静压导轨连接器、中心悬浮体以及扩展台面。对可动部分进行四面体网格划分,其余结构视为刚体。
振动台运动部件之间的螺钉连接可以用约束六自由度的MPC单元等效成接触面之间的刚性连接。三轴向振动台通过平动式静压导轨连接器进行各个激励方向上的空间解耦,平动式静压导轨连接器与中心悬浮体之间的连接可以使用动圈轴向单自由度MPC单元进行接触区域之间的连接。振动台仿真模型共包含40 856个四面体十节点单元和1 331个MPC单元。有限元模型如图2所示。

图2 三轴向电动振动台有限元模型Fig.2 Finite element model of three-axial electric shaker
将动圈四周的4个U型弹簧当做可动部分处理。在建立振动台动圈时,直接将U型弹簧与动圈建立为统一的整体,进行统一的网格划分,在定义材料属性时对U型弹簧和动圈分别进行材料属性定义。同时对U型弹簧外侧面进行固支处理。
在MPC单元的单个节点上施加轴向力而使得整个动圈产生均匀的轴向力,模拟动圈的实际受力状态。
2.2 振动控制方法
2.2.1 频响分析
频响分析的目的是获得振动台系统监测点与激励点之间的频响函数矩阵。为了获得三轴向振动台三个动圈底部激励点和控制点之间的总频响函数矩阵,在三个动圈底部分别施加动圈轴向单位力进行正弦扫频,根据方程x(iω)=H(iω)f(iω)得到控制点与每个激励点之间的频响曲线。
考虑到三个方向的正交性,可以获得三轴向电动振动台仿真模型三个动圈激励点与扩展台面上控制点之间的总体频响函数矩阵为:
(1)
式中:加号前边的H为传递函数实部;加号后边的H为传递函数虚部。
2.2.2 正弦振动控制

(2)
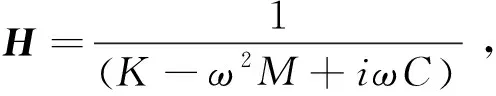
(3)
(4)

在正弦载荷激励下,三轴向电动振动台仿真系统的正弦控制响应计算过程如图3所示。

图3 正弦响应计算原理框图Fig.3 Block diagram for calculation principle of sine response
2.2.3 随机振动控制
在对三轴向振动试验系统进行随机振动控制之前,首先需要确定控制点处的功率谱密度曲线。由于本振动试验系统为三维输入,不仅要考虑每个激励点处的自功率谱密度,还要考虑激励点与激励点之间的互功率谱密度。同时需要兼顾所关注频段内的均方根值。均方根值是表征能量的一个参数。如果此值过大,容易引起振动台上的产品由于能量过大而损坏[13-15]。
在确定激励点之间的互功率谱密度Sxy(ω),Syz(ω),Szx(ω)时需要设定激励点之间的相干系数。两个平稳随机过程x(t),y(t)之间的相干函数定义为:
(5)
式中:|γxy|=1时,x(t)与y(t)之间存在线性关系,且系统必为线性系统;
|γxy|<1时,值越接近于1说明x(t)与y(t)之间存在线性关系的可能性越大;
|γxy|=0时,表示x(t)与y(t)之间完全不相干,二者相互独立。此方程所描述的是两个信号在各个频率处的相关程度。
(6)
其中
得到振动台动圈激励点力输入谱SF后,可以通过在Patran中进行随机振动计算来获取所关注位置处的功率谱密度曲线以及查看相关的应力分布情况,同时也可以输出控制点位置的功率自谱密度曲线。如果输出的控制点位置的功率谱密度曲线与参考谱相同,说明随机振动控制计算原理正确。
在随机载荷激励下,三轴向电动振动台仿真系统的随机控制响应计算过程如图4所示。

图4 随机响应计算原理框图Fig.4 Block diagram for calculation principle of random response
3 三轴向虚拟振动试验算例
3.1 试验件模型
试验件由框架、喷管、氧化剂导管和燃料导管等组成。加速度测点分别安装在试件的喷管低端位置和氧化剂导管中部位置。应变片贴在氧化剂导管根部。试验件框架四周的螺栓孔位置附近为固定位移约束。
3.2 三轴向虚拟正弦振动试验
三轴向虚拟正弦振动试验范围为20~2 000 Hz。试验加速度控制点定义为与试验件框架连接的试验夹具上某一点。设定结构临界阻尼系数为0.02。控制点在三个动圈激励方向上的加速度曲线均设定为如图5所示曲线。使用相同的方法对三个动圈下方MPC点分别施加正弦激励来分别进行单轴正弦激励。相关参数设置及监测点加速度幅值曲线均与三轴向正弦振动仿真相同。

图5 控制点加速度曲线Fig.5 Acceleration curve of reference control point
将试验件与三轴向虚拟振动试验系统进行联合仿真,并将虚拟正弦振动试验条件施加给虚拟振动试验系统进行虚拟振动试验。图6为可视化的试验件与三轴向虚拟振动台联合的虚拟振动试验系统。

图6 试验件与三轴向振动台有限元模型Fig.6 Finite element model of specimen and three-axial shaker
提取单轴向正弦激励与三轴向正弦激励条件下产品上关注点的加速度幅值曲线,以观测研究频段内关注点加速度的整体分布情况和对应频率下的最大幅值。图7给出的是产品某一关注点处在三轴向同时激励下和单轴向分别激励下的加速度响应曲线。由图7可知,三轴向同时激励下,监测点加速度最大响应都是在低频段。与3个方向分别进行单轴激励相比,单轴激励下的各个峰值在三轴向同时激励时均体现了出来。三轴向同时激励下各个峰值的加速度幅值均有一定程度提高,并且激发出了更多的加速度峰值。

图7 氧化剂导管中部加速度幅值曲线Fig.7 Acceleration amplitude curves in middle of the oxidant tube
3.3 三轴向虚拟随机振动试验
虚拟随机振动试验范围为900~1 000 Hz。结构临界阻尼系数设为0.02,3个激励点之间的相干系数设定为1.0,即各个激励点之间完全相干。试验条件如表1所示。选取产品与夹具连接面上一点为控制点。

表1 窄带随机振动激励条件
图8为游机机组氧化剂导管在x,y,z三个正交方向分别激励下的应力Mesis云图以及游机机组氧化剂导管在三轴向同时激励下的应力Mesis云图。

(a)x向激励下应力Mises云图 (b)y向激励下应力Mises云图

(c)z向激励下应力Mises云图 (d)三轴向激励下应力Mises云图
图8应力Mises云图
Fig.8Misesnephogramofstress
从图8中可以看出,无论是x,y,z单向激励或三轴向同时激励,产品氧化剂导管的最大应力所在区域都是氧化剂导管与摇摆轴连接位置附近。对氧化剂导管与摇摆轴连接处附近某一单元进行应力值提取,并与相同位置的试验结果进行对比,结果如表2所示。

表2 仿真结果与试验结果应力值对比
从对比结果可以看出,单轴向激励时仿真结果与试验结果的偏差在允许范围内。同时在三轴向激励下,获得的该监测点的应力值为151 MPa。对比发现,三轴向激励下该单元位置的应力值较单向激励时都较大。计算仿真试验中单向激励下该点在三个方向上的应力的矢量和为109.5 MPa。对比此结果与三轴向激励下的结果可以发现二者相差较大。因此得出,三轴向激励并不能用单轴向激励的空间矢量叠加来等效,必须考虑三轴向激励下的空间耦合作用。
4 结论
本文采用理论分析、数值仿真与试验相结合的研究手段,开展了液体火箭发动机三轴向虚拟振动试验研究。将某试验件与三轴向振动台进行联合建模,通过相关控制方法进行了试件的三轴向虚拟正弦振动试验和虚拟随机振动试验,可以得到以下结论:
1)通过相关公式推导及计算获得了三轴向正弦振动和随机振动的控制方法,相关方法获得的控制谱与参考谱完全相符。
2)三轴向虚拟正弦振动试验与单轴激励相比在所研究的频率范围内多出了部分共振峰,分析认为某些峰值是由三轴向同时激励的耦合作用所产生。
3)从虚拟随机振动试验应力Mises云图可以看出,游机机组氧化剂导管与摇摆轴连接部位的应力值最大,最容易发生故障。相比单轴向激励,三轴向同时激励时应力值大,且三轴向激励的结果并不等效于单轴激励时简单的矢量叠加,必须考虑三个方向同时激励的耦合作用。因此在实际的三轴向振动试验中,如果仍采用单轴的试验参考谱同时施加在三个方向,可能会导致单向激励通过的试验三轴向无法通过,需要根据虚拟试验的结果指导实际参考谱的剪裁和修正。

