大气折射对电视制导导弹定位精度的影响分析

刘燕，袁莹涛，郭翔，索涛,*，李玉龙，于起峰, 3

1. 西北工业大学 航空学院，西安 710072 2. 陕西省冲击动力学及工程应用重点实验室，西安 710072 3. 国防科技大学 航天科学与工程学院，长沙 410073

电视制导导弹以其机动、灵活、快速响应、制导精度高、可对超低空目标或低辐射能量目标进行探测跟踪等优点已被广泛应用于世界各国的空地攻击武器系统[1-2]。美国的AGM猛禽系列中程空地导弹、俄罗斯的KH系列空地导弹和英国的Bristol RP 8空地导弹等都采用了电视制导体制。该制导方式把电视摄像机作为目标图像的传感器，利用可见光被动制导，所以图像分辨率高、抗无线电干扰能力强[3]。但是以电视摄像机为主要部件的光学成像系统对光的干扰也较为敏感，易受气象条件的影响。在实际作战过程中，目标打击区域内的温湿度、风速、密度、气压等大气状态要素的变化均可引起大气折射率的改变，进而导致从目标反射出的光线在到达像平面的传输路径上发生折射，最终造成导弹光学系统接收到的是存在大气折射误差的目标图像。这将大大影响其探测、识别和跟踪目标的能力，降低电视制导导弹击中目标的准确度，甚至脱靶。

因此，大气折射误差对制导精度的影响分析是电视制导导弹设计研发过程中必须考虑的关键因素之一。目前，关于大气折射对电视制导导弹定位精度影响的讨论较少，研究较多的是对比度、能见度和烟雾干扰对电视制导导弹命中概率的影响[4-5]。因此，本文基于大气折射模型，通过光线追迹方法，研究了大气折射效应对电视制导导弹对目标定位的影响。首先给出了常用的5种大气折射指数模型，分析了其随高度的分布规律，并通过探空仪5天实测的大气参数计算出大气折射率分布，对模型的有效性进行了验证。然后，通过分析电视制导导弹的大气折射误差原理，提出了以定位误差和俯角误差为大气折射效应评价标准的电视制导导弹大气折射误差模型。由于本文所研究的大气层内折射率分布情况复杂且呈不规则分布，难以求得大气折射误差的解析解。根据这一情况，本文采用4阶Runge-Kutta光线追迹方法插值计算光线传播方程，进而求得地面目标反射的光线到达摄像机成像平面的曲线传播路径，从而获得大气折射误差。最后，基于所给的5种大气折射率模型，对不同发射高度和俯角的情况进行仿真分析，从而可以先期预测电视制导导弹对打击目标定位的偏离程度，也可对导弹的精度进行评估。

1 大气折射率模型

造成电视制导导弹折射误差的关键因素是成像光路上大气折射率的变化，只有确定了大气折射率的空间分布模式，才能进一步研究电视制导导弹的大气折射效应。某型电视制导空地导弹的发射高度一般在200～5 000 m，处于对流层区域内。根据大气物理学可知，在可见光频率范围内，对流层大气折射率是温度、大气压和水汽压的函数[6-9]：

(1)

式中：p为大气压强，hPa；T为大气的热力学温度，K；e为大气中水汽分压强，hPa；n为大气折射率，它的值非常接近于1， 所以用大气折射指数N表示更为方便[10]。

在对导弹目标定位的俯角数据作折射修正之前，用氢气球携带GPS探空仪升空或其他气象观测设备[11]，可以测出随高度实时变化的大气温度、气压、湿度等数据。如图1所示，为中国西南某观测站在2018年6月1日、6月5日、6月10日、6月20日和6月25日共5天的0时实时探测的大气参数(温度、大气压力和水汽分压)随高度h的变化情况。

由图1可以看出在实际时空条件下利用探空仪所测的大气参数随高度变化离散性较大，难以覆盖电视制导导弹大气折射误差修正所需的所有高度的大气折射率值。将图1中5天观测的温度、大气压力和水汽分压数据代入式(1)计算可得出大气折射指数随高度的变化，如图2所示。

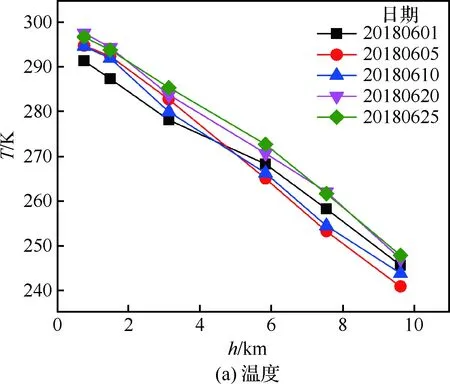
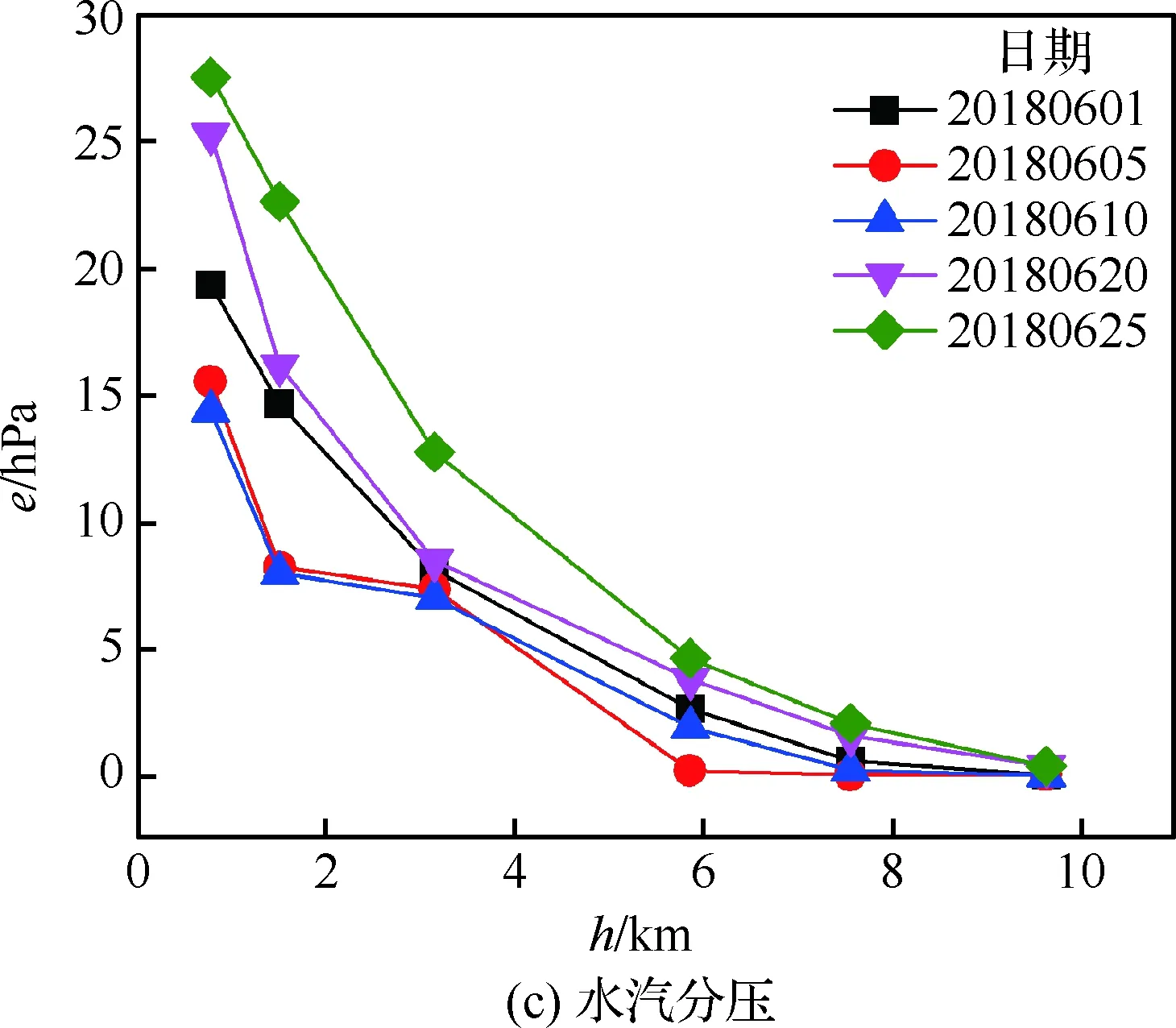
图1 大气参数随高度的变化曲线Fig.1 Changes of atmospheric parameters with altitudes

利用探空仪实时获取大气参数来计算得到大气折射率的方法，虽然精度高，但是很费时，而且释放探空气球需要人员和大量经费的投入。考虑到各种实际条件的局限性，实时获得大气参数有时较为困难。大量统计结果表明，大气折射指数N(h)具有相当稳定的统计特性。从大气的平均分布模式考虑，线性模型、指数模型、3段模型、双指数模型和Hopfield模型等大气折射指数高度分布模型应用比较广泛[9, 12-13]。在没有实时探空数据的情况下，这些统计模型能够较好地反映出大气折射率变化趋势。因此，本文基于上述大气折射指数简化的经验模型，与高精度的光线追迹算法相结合，以此建立电视制导导弹大气折射误差模型；并利用实时探空的大气参数来验证大气折射指数经验模型的有效性，以满足对电视制导导弹大气折射效应高精度修正的需要。

1) 线性模型

N(h)=N0+ΔN(h-h0)

(2)

式中：N(h)为高度h处的大气折射指数；N0为地面折射指数，N单位；ΔN为大气折射指数的梯度，N单位/km；h为海拔高度，km；h0为地面的海拔高度，km。线性模型适用于低层大气，计算十分简单，通过大量测量和统计分析可知，在近地面0.1 km范围内线性模型与实际数据之间吻合较好，若超出该范围，则线性模型误差较大[9]。

2) 指数模型

N(h)=N0exp(-c0(h-h0))

(3)

式中：c0为指数衰减系数，1/km。大量统计结果表明，在海拔高度大于1 km范围内，平均大气折射率用指数模型近似精度较高。

3) 3段模型

前述两种模型各有适用区域，对低层(1 km以下)大气应取线性模型；1～9 km区域采用指数模型；9 km以上区域则采取另外一种指数模型，方能更加精确地描述整个剖面。于是有如下3段模型[11]：

N(h)=

(4)

式中：N1为离地面1 km处的大气折射指数；c1为地面以上1 km至海拔9 km的指数衰减系数，1/km；N9为海拔9 km处的大气折射指数；c9为海拔9 km至海拔20 km的指数衰减系数，1/km。

4) 双指数模型

式(1)中，右端第1项代表折射率的干项，而包含水汽压的第2项则表示折射率的湿项。经统计分析知，这两项均随高度增加而按指数衰减，并且湿项的衰减比干项快得多[13]。因此，分别用两个指数来表示：

(5)

式中：Nd0和Nw0分别为干、湿两项的地面折射率值；Hd和Hw分别为干、湿两项衰减到地面值1/e的高度，km。

5) Hopfield模型

Hopfield也将折射率分为干、湿两项，表示为高度的4次方函数[14]。这种剖面与世界各地的平均折射率剖面吻合较好。该模型的形式为

N(h)=Nd(h)+Nw(h)

(6)

式中：

(7)

(8)

式中：Hd为折射率中干项衰减为零的高度，km，Hd=40.136+0.148(T0-273.15)，T0为地面温度；Hw为折射率中湿项衰减为零的高度，Hw=11 km。

为便于分析比较，图1中中国西南某观测站上述5种模型所包含参数的具体取值如表1所示[13]。根据表1中的参数，并考虑到电视制导导弹发射高度在5 km以下的对流层区域内，因此仅计算该范围内上述5种模型的大气折射指数随高度变化情况，如图2所示。

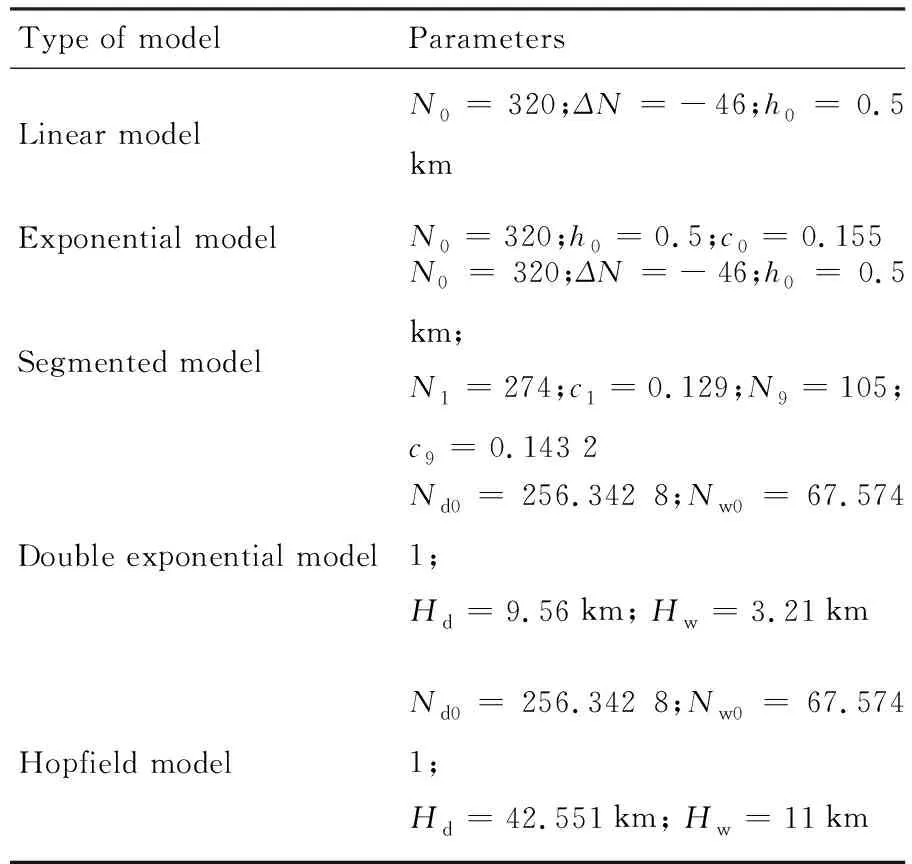
表1 5种大气折射模型包含的相关参数取值

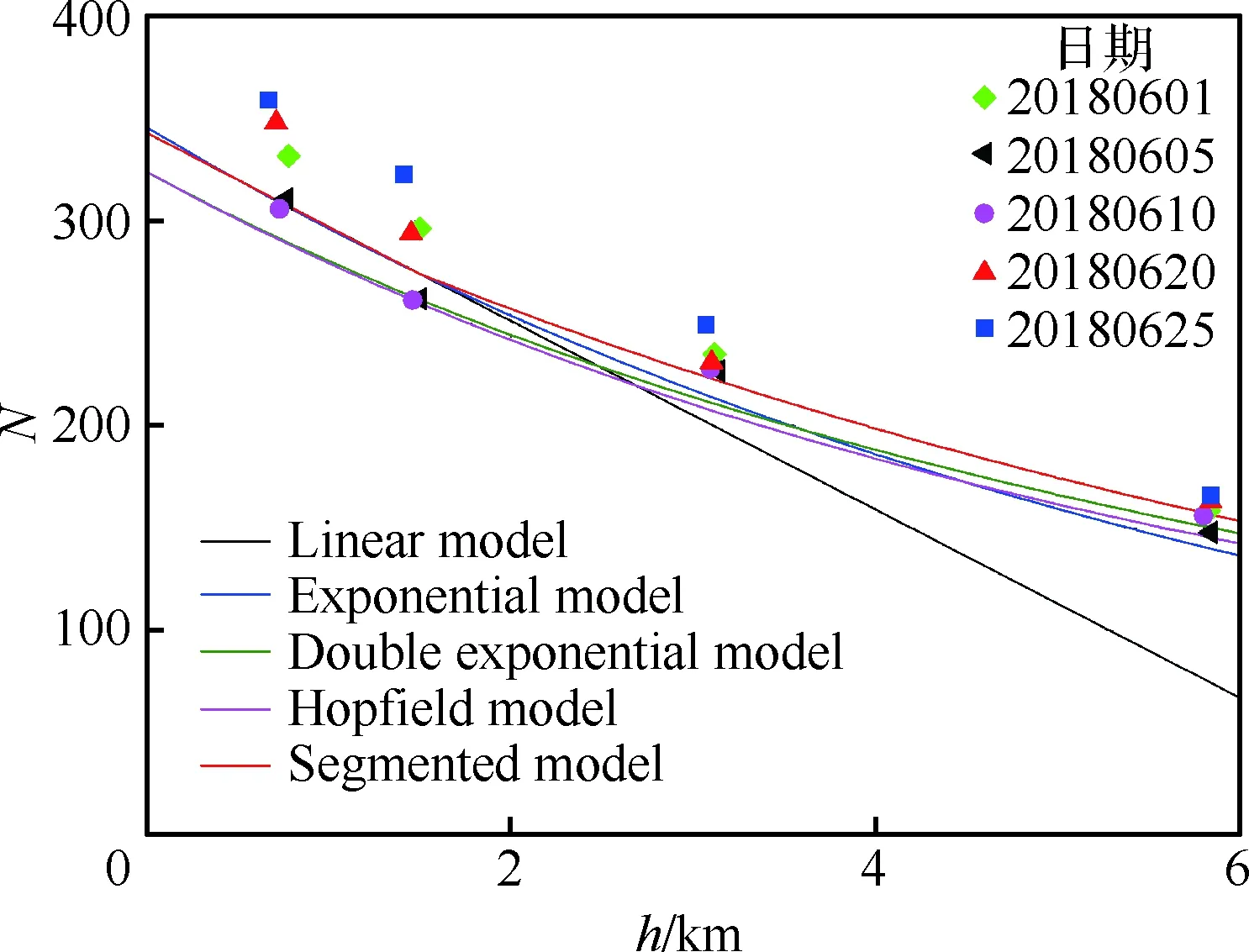
图2 大气折射指数随高度的变化Fig.2 Atmosphere refractivity vs altitude

由图2可以看出，大气折射指数随着高度的增加逐渐减小；这5种大气折射经验模型能够较好地反映出大气折射率变化趋势，且大气折射率分段模型与多次实时探空数据的一致性最好；线性模型在高海拔条件下，相对其他模型偏差较大。

2 电视制导导弹大气折射误差模型

在导弹对目标定位中，成像光线的大气折射误差主要表现为俯角误差Δθ和定位误差ΔS。

俯角误差是导弹电视摄像机对地面目标T的实测视在俯角θ与真实俯角θ0之差为

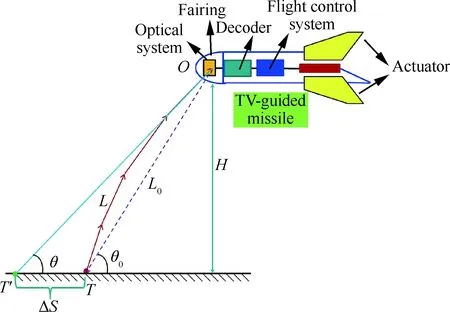
图3 电视制导导弹大气折射误差模型Fig.3 Atmospheric refraction error model of TV-guided missiles

Δθ=θ-θ0

(9)

定位误差则是目标的实际位置T和成像虚位置T′之间的地表距离为

(10)

3 光线追迹

3.1 算法描述

由于大气层内折射率情况复杂且呈不规则分布，难以求得地面目标反射的光线到达摄像机成像平面沿曲线传播的解析解[15-18]。根据这一情况，本文通过数值方法插值计算光线传播方程进行光线追迹：

(11)

求解光线方程的方法有很多，例如欧拉法、泰勒级数法、3阶Runge-Kutta法和4阶Runge-Kutta法等[19-21]。其中4阶Runge-Kutta法的精度较高[22]，本文采用4阶Runge-Kutta法作为光线追迹方法。

式(11)不便于直接积分，通过引入新变量改变它的形式，定义为

(12)

于是光线方程式(11)可简化为2阶微分形式：

(13)

定义光线矢量为

(14)

则式(13)可进一步可以转化为1阶微分方程组：

(15)

根据4阶Runge-Kutta方法，追迹光线的数值计算公式为

(16)

式中：Δt为光线追迹步长；K1为光线初始位置r0处的方向矢量，L1为r0处折射率和折射率梯度向量的乘积；K2为光线由初始位置插值的r0+ΔtK1/2处的方向矢量，L2为r0+ΔtK1/2处折射率和折射率梯度向量的乘积；K3为光线初始位置r0+ΔtK2/2处的方向矢量，L3为r0+ΔtK2/2处折射率和折射率梯度向量的乘积；K4为光线初始位置r0+ΔtK3处的方向矢量，L4为r0+ΔtK3处折射率和折射率梯度向量的乘积；它们具体取值为：

(17)

(18)

(19)

(20)

通过给定光线的初始位置r0和光线的初始入射方向T0，可以求得该步长末端的r1(位置)和T1(光线的轨迹方向)，并以此作为下一步追迹的初始条件，按照步长Δt逐步追踪直至完成整个过程。

3.2 算法验证

对于第2节中的大气折射率分布，无法从光线方程推出光线轨迹的解析解。但对一些特殊的折射率分布却是可以获得解析解的。对于二维折射率径向分布介质，其折射率可表示为

(21)

式中：α为折射率分布参数；n0为中心轴上的折射率[20]。

当初始入射点位置为(1/(n0α),0)、初始入射方向垂直于x轴时，光线穿过该折射率场的轨迹解析解为

(22)

令n0=1.5,α=0.01 mm-1，则式(20)的折射率分布如图4所示，式(21)中实际光线轨迹和由光线追迹算法仿真获得的光线轨迹如图5所示。

图4 4阶Runge-Kutta光线追迹方法精度 验证的折射率分布云图Fig.4 Index of refraction field for precision test of fourth-order Runge-Kutta ray-tracing method

图5 不同步长的4阶Runge-Kutta光线 追迹结果与精确解的比较Fig.5 Comparison of different ray tracks for precision test of fourth-order Runge- Kutta ray-tracing method

定义y轴处对应的光线真实传播轨迹的矢量r′，通过Runge-Kutta方法若干步追迹后的计算值为r，定义解析解与计算值的相对误差为

(23)

根据式(22)可计算出，当步长Δt=1 mm时，Runge-Kutta方法追迹精度达10-6；当步长为0.1 mm 时，计算精度达10-7。从图5也可以看出，随着追迹步长的减小，4阶Runge-Kutta方法追迹的光线和解析解几乎重合，计算误差基本可以忽略。另外，由图2可以看出，本文所研究的大气折射率的幅值变化远远小于该验证实例，因此采用4阶Runge-Kutta光线追迹方法研究电视制导导弹的大气折射效应是合适的。

4 仿真与分析

考虑到某型电视制导导弹在实际作战中的一般飞行高度和俯角，这里假定导弹的发射高度h为0.5～5 km(每步间隔0.5 km)，导弹对目标定位时所测的俯角θ范围为2°～45°。

4.1 基于5种大气折射模型的折射误差

首先采用第3节的4阶Runge-Kutta光线追迹方法，令追迹步长为0.1 m，基于第1节所给的5种大气折射经验模型和探空实测大气参数计算的大气折射率值，选取导弹锁定目标时所测俯角分别为2°和20°时，通过MATLAB软件计算大气折射效应引起的俯角误差Δθ和定位误差ΔS与导弹海拔高度的关系，分别如图6和图7所示。

通过对图6和图7分析比较可知：

1) 用经验模型计算的定位误差和基于实际时空条件下大气参数的定位误差近似性较好。在低海拔范围，利用本文所提出的光线追迹方法二者计算的结果几乎完全一致；在高海拔区域，由于实际大气参数数据离散性大，经验模型计算结果偏差稍微变大。因此，本文的大气折射经验模型是有效的。

2) 基于3段模型的大气折射误差要小于其他模型，且与实时探空数据计算的结果一致性最好；基于线性模型计算的大气折射误差要高于其他四种模型，且差异较大。这是由大气折射率随高度的分布特点所决定的，由图2的大气折射指数随高度变化曲线可以看出，在高海拔时，对于同一高度，线性模型的大气折射指数最大，三段模型最低。根据Snell定律[23]，光线进入折射率连续变化介质的入射角正弦值和折射率成反比。在导弹视在俯角即光线入射角θ不变的情况下，折射率越大，光线的出射角越小，由式(9)可知光线偏折也就更严重。因此在高海拔时，基于这5种大气折射模型计算出的大气折射误差与其折射率分布是一致的。

图6 导弹视在俯角θ=2°和20°时，基于5种经验 模型和探空仪实测大气参数的定位误差对比Fig.6 Location error vs altitude for θ=2° and 20° based on five atmospheric refraction model and atmospheric parameters from radiosonde

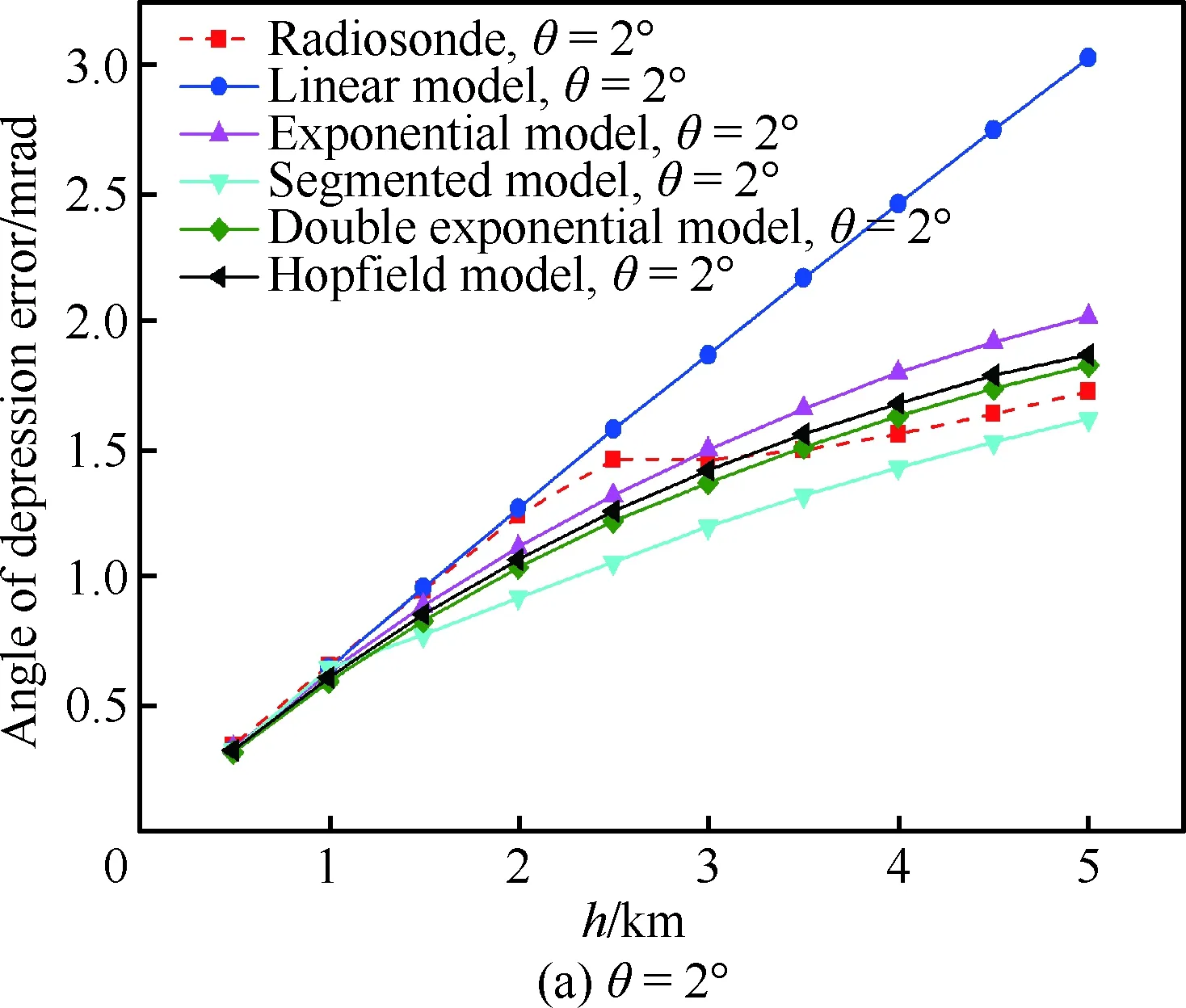
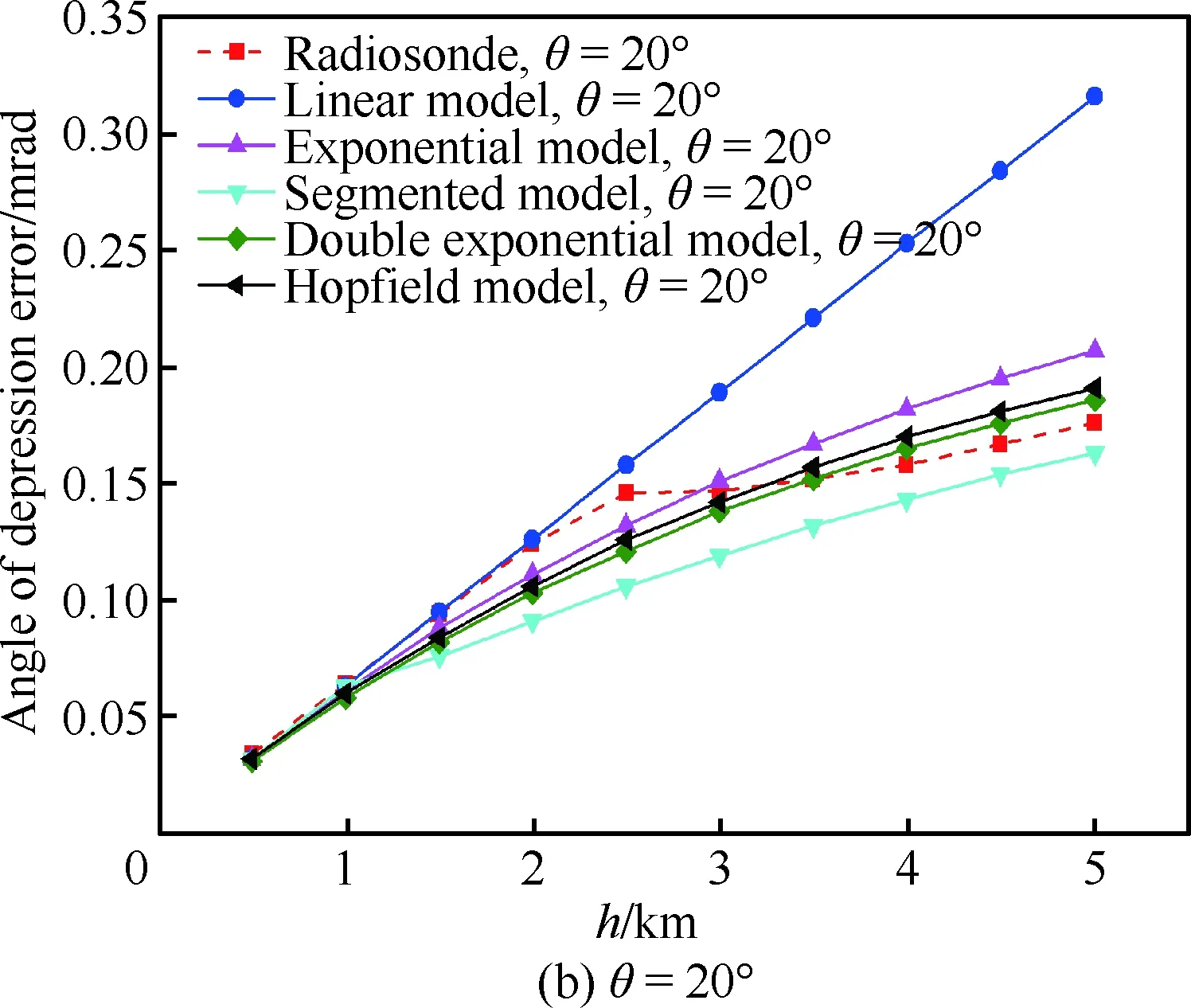
图7 导弹视在俯角θ=2°和20°时，基于5种经验 模型和探空仪实测大气参数的俯角误差对比Fig.7 Angle of depression error vs altitude for θ=2°and 20°based on five atmospheric refraction model and atmospheric parameters from radiosonde

3) 在导弹对目标定位的视在俯角相同的情况下，随着发射高度的增加，5种模型计算的大气折射定位误差和俯角误差均逐渐增大。这是因为随着高度的增大,光线穿过大气介质的距离L在增大，因此电视制导导弹对目标定位的折射误差也在增大。

由图6可知，在发射高度相同情况下，定位误差随着视在俯角的增大迅速减小。例如，发射高度为5 km、视在俯角为2°时基于3段模型计算的的定位误差ΔS高达6.34 km，相同高度下20°时的ΔS仅为6.98 m，前者约为后者的1 000倍。这同样可以由Snell定律解释，在导弹发射高度相同的情况下，光线在介质中传播的出射角正弦值和入射角正弦值成正比。导弹视在俯角θ越小，则光线在介质中传播的入射角就越大，出射角也就随之变大，光线在目标和导弹电视摄像机之间的大气介质中传播的距离也就更长，因此，大气折射误差也积累的更大。

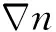
4.2 导弹视在俯角对大气折射误差的影响

因为通过对图6和图7分析比较可知，电视制导导弹的大气折射误差对发射俯角比较敏感；用3段经验模型计算的定位误差和基于实际时空条件下大气参数的结果近似性较好且都低于其他模型；另外先前的研究也表明，折射率3段模型能够较好地反映出大气折射率变化趋势，且与多次探空数据的平均值一致性较好[11]。所以，下文以3段模型为代表，进一步研究导弹发射视在俯角对其大气折射误差的影响。选取3°、4°、5°、6°、10°、15°、20°、25°、30°、35°、45°的视在俯角，计算大气折射误差，相应的俯角误差Δθ和定位误差ΔS随导弹海拔高度的变化曲线，如图8和图9所示。

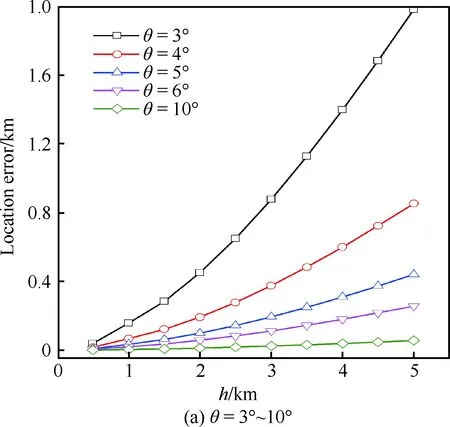
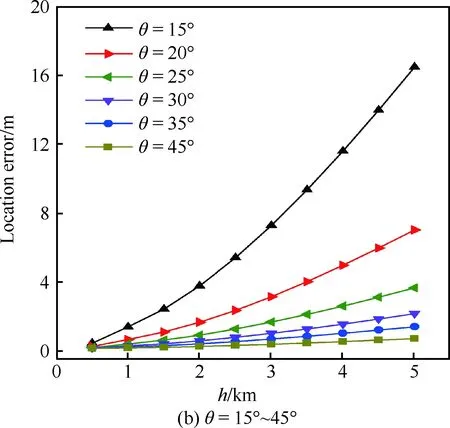
图8 导弹视在俯角θ=3°～45°基于3 段模型的定位误差Fig.8 Location error based on segmented refraction model vs altitude for θ=3°-45°

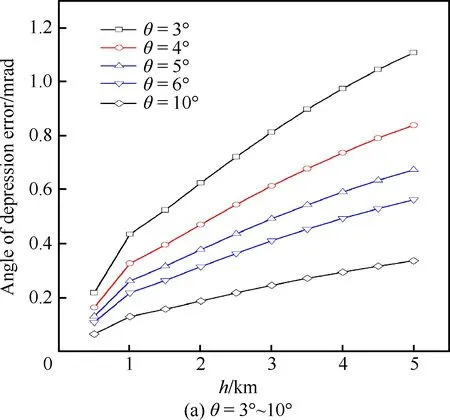
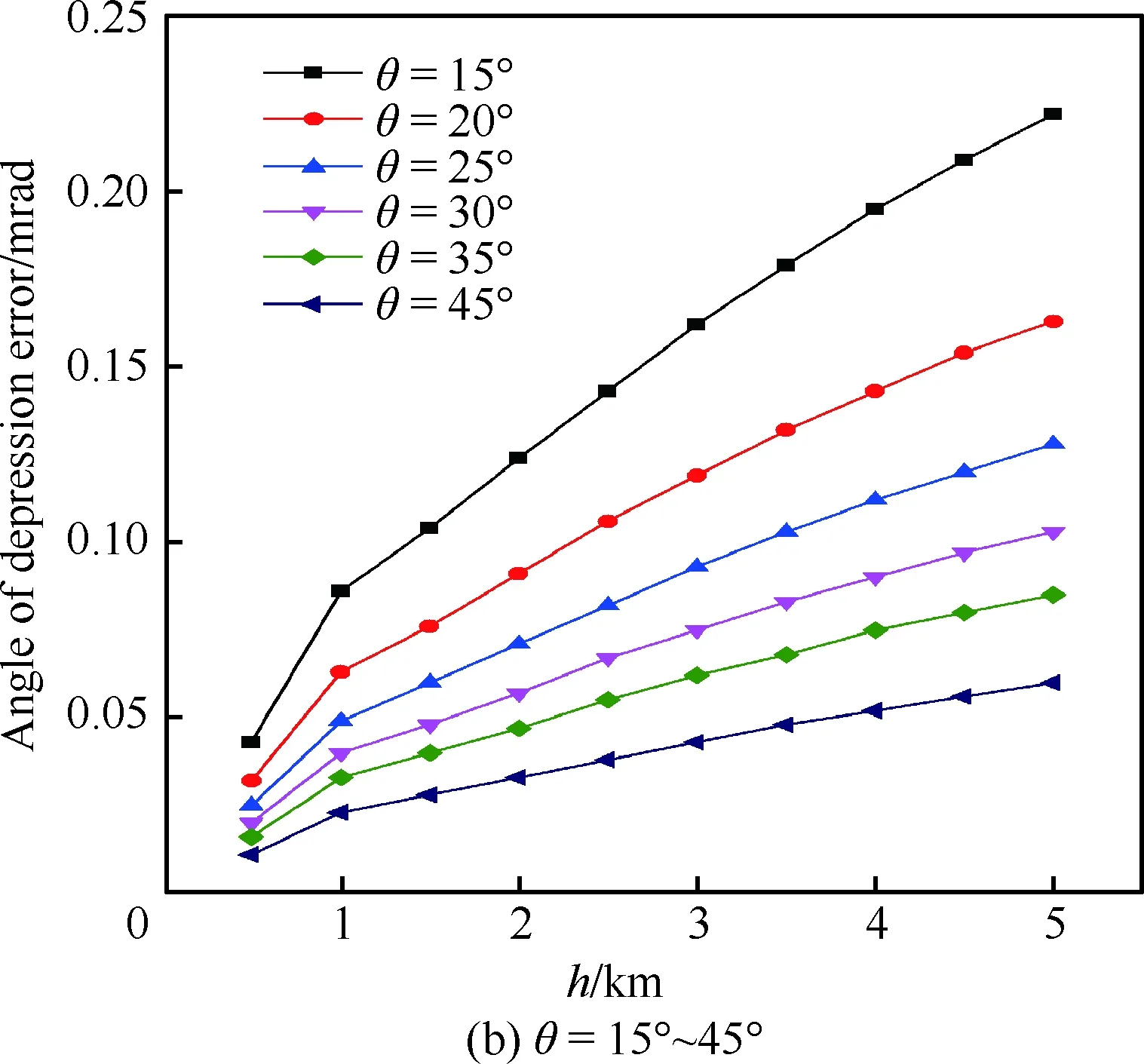
图9 导弹视在俯角θ=3°～45° 基于3段模型的俯角误差Fig.9 Angle of depression error based on segmented refraction model vs altitude for θ=3°-45°

通过将图8和图9比较可以发现：当发射高度一定时，俯角误差和定位误差均随导弹视在俯角的增加而迅速减小，这说明光线的俯角越小，大气折射效应越强；视在俯角θ小于5°时，5 km高度发射的大气折射定位误差将超过500 m；而θ大于30°时相应的定位误差仅在2 m以内。另外，随着导弹视在俯角的增加，大气折射的误差曲线逐渐吻合。因此，为了减小大气折射造成的电视制导导弹对目标的定位误差，选取30°以上的发射俯角对目标进行定位打击较好。

从图9可以看出，俯角误差在高度1 km处出现明显的转折，这是因为3段模型在0～1 km和1～9 km采用的大气折射指数经验公式不同，前一段采用的是线性模型，后一段采用的是指数模型，而且相同高度下指数模型的折射率梯度要比线性模型的折射率梯度大。

5 结 论

1) 提出了一种基于大气折射率模型，以高精度的4阶Runge-Kutta光线追迹方法为计算手段，以定位误差和俯角误差为大气折射效应评价标准的电视制导导弹大气折射误差模型。基于经验模型的仿真结果和探空实测大气参数的结果近似性较好，而且该结果和雷达信号、闪电等大气折射问题的对流层折射误差[13, 24]在数值上是一致的，验证了本文模型的正确性和可信度。

2) 基于3段模型的大气折射误差要小于其他模型，且折射率分布与实时探空数据一致性最好，是一种较为精确的模型。实际应用中，在没有实时GPS探空数据的情况下，可利用该经验模型定量计算大气折射对电视制导导弹造成的定位误差，并予以提前修正从而提高制导精度。

3)相同高度下导弹发射的视在俯角扩大10倍，由大气折射造成的定位误差和俯角误差将分别缩小1 000倍和10倍；5 km高度、视在俯角为30°时的定位误差已减小到2 m以内。因此，在电视制导导弹总体方案设计阶段，本文的模型可以辅助制导精度的评价以及系统的设计；在实际作战过程中，本文的结论对导弹飞行轨迹的规划以及提高打击能力具有积极的指导作用。