压电陶瓷叠层作动器迟滞蠕变非线性自适应混合补偿控制方法

赵天，杨智春，刘昊，Kassem MOHAMMED，王巍

西北工业大学 航空学院，西安 710072

压电陶瓷作为一种新型功能材料在航空航天领域中如结构抖振主动控制、伺服气弹、能量回收等方面得到了广泛的应用[1-2]。压电陶瓷作动器是利用压电材料的逆压电特性，在输入电压或电流的作用下产生形变，达到机械运动的目的，因而能保证纳米级分辨率运动，有着传统电机驱动不可比拟的优势。但是，压电陶瓷作动器在输入信号和输出位移关系上存在复杂的迟滞非线性(Hysteresis Nonlinearities)[3]。该迟滞非线性表现为多值映射性、记忆性以及率相关动态迟滞特点[4]。在主动控制应用中，压电作动器的迟滞蠕变非线性特性轻则影响控制系统的控制效果，重则降低系统的稳定性甚至导致控制系统失效。因此，压电陶瓷作动器的迟滞蠕变补偿控制方法的研究对提高主动控制系统稳定性以及控制精度具有重要的理论意义和实践意义。

目前迟滞模型大致可分为基于迟滞算子的迟滞模型与基于微分方程的迟滞模型。基于迟滞算子的迟滞模型通常为简单的分段线性迟滞环，需要多个基本算子的叠加来增加迟滞曲线光滑程度，如Preisach模型[5-6]、Prandtl-Ishlinskii (PI)模型[7-8]、Krasnosel’skii-Pokrovskii (KP)模型[9]等，但这些模型都存在着模型参数较多难以辨识、形式复杂以及无法反映迟滞现象的动态效应等缺点。基于微分方程的迟滞模型，如Dahl模型[10]、Bouc-Wen模型[11-12]、Duhem模型[13]等，可以反映迟滞动态特性，但也存在对压电陶瓷迟滞特性描述不完整的缺点。

关于压电作动器的迟滞蠕变补偿研究，常用的方法是构造逆迟滞模型进行前馈补偿。但理论上难以建立精确的逆模型，同时在实际工程应用中，输入信号的变化以及环境因素会降低其补偿精度。第2种是直接补偿控制[14]，即直接设计控制器对迟滞蠕变特性进行补偿控制。不需进行复杂的迟滞逆模型求解，同时可以根据参数变化进行动态补偿控制，但存在控制器设计复杂、控制精度较差等缺点。另外，也有学者开展反馈控制策略的研究，如PID控制[15]、滑模控制[16]、鲁棒控制[17]等。

本文提出了一种迟滞逆模型前馈补偿与自适应滤波器反馈补偿控制相结合的前馈-反馈混合补偿方法，对压电作动器迟滞蠕变非线性进行补偿控制。基于有限脉冲响应(FIR)横向滤波器结构的最小均方差算法，设计得到自适应滤波器进行控制反馈。并进行自适应混合补偿控制实验研究，与常规前馈补偿进行对比，验证本文方法的有效性及其在动态特性与跟踪精度方面所具有的优势。

1 改进PI迟滞蠕变模型

PI模型结构简单，参数较少，且存在解析的逆模型，在迟滞非线性的建模及补偿问题研究中得到较为广泛的应用。由于传统的PI模型具有奇对称性，对实际的非对称迟滞曲线描述不准确，在开环逆迟滞补偿控制中对期望位移的跟踪精度不高[18]。因此，为了精确描述非对称的迟滞非线性特性，本节采用改进的PI迟滞蠕变(MPI)模型，并构造出相应的逆解析模型。

1.1 迟滞建模

迟滞算子H可由nH+1个基本play算子的线性加权积分得到[19]：

(1)

式中：wHi为权系数；rHi为阈值；zH0i(i=0,1,…,nH)为初值。play算子定义为分段单调时间区间t0≤t1≤…≤tj≤t≤tj+1≤…≤te的输入信号的递推关系，即

zH(t)=max{x(t)-rH,min{x(t)+rH,zH(tj)}}

(2)

其中：初值为

zH(t0)=max{x(t0)-rH,

min{x(t0)+rH,zH(t0)}}

(3)

叠加算子S描述迟滞算子H的奇对称特性的偏差，可由2nS+1个SrS算子加权线性叠加[20]而得:

(4)

式中：wS i为权系数；rS i为阈值。

MPI迟滞算子定义为由迟滞算子H和叠加算子S的串联，式(6)以向量的形式表示:

Γ[x](t)=S[H(x)](t)

(5)

(6)

式中：HrH和SrS分别为nH+1维迟滞算子向量和2nS+1叠加算子向量；wH和wS分别为相应的权系数向量；zH0为迟滞算子的初值向量。

1.2 lg(t)型蠕变建模

压电作动器的输出位移对时间的蠕变效应称为蠕变特性，其位移蠕变与时间呈对数变化关系，即lg(t)型蠕变动态过程，可以由lg(t)型蠕变算子描述[21]：

(7)

式中：m为蠕变特征值个数

lg(t)型蠕变算子zK(t)=KrKaK[x,zK0](t)为式(8)所示非线性微分方程的唯一解。

min{x(t)-zK(t)+rK,0}}

(8)

式中：zK0为初值；rK∈R+为权系数；aK∈R+为蠕变特征值。

(9)

式中：Ts为时间序列的最小间隔。

MPI蠕变算子由nK+1个阈值为rKi的lg(t)型蠕变算子加权叠加得到：

(10)

式中：wKi为权系数，rKi为阈值。

将MPI蠕变算子与MPI迟滞算子结合起来，就得到MPI迟滞蠕变模型，可以完整地描述非线性过程中的迟滞特性和lg(t)型蠕变特性。

Γ[x](t)=S[H[x]+K[x]](t)=

(11)

式中：KrK为nK+1维蠕变算子向量；wK为蠕变算子权系数向量；zK0为蠕变算子的初值向量。

2 自适应混合补偿控制

2.1 迟滞蠕变补偿模型

采用逆模型控制理论补偿压电作动器迟滞蠕变非线性的基本思想为：建立迟滞蠕变逆模型，并将期望的输出信号作为逆模型的输入信号，将逆模型的输出作为平台的控制信号，使得期望输出位移信号经过逆模型与平台之后，可以实现输入信号与输出信号一一映射的线性关系[22]：

Γ-1[y](t)=H-1[S-1[y]](t)=

(12)

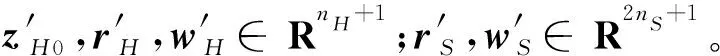
(13a)

(13b)

i=1,2,…,nH

(13c)

(13d)

(13e)

2.2 MPI迟滞蠕变模型参数辨识方法

基于测试得到的输入信号x(t)以及其相应的输出信号y(t)，建立MPI迟滞蠕变模型Γ及其逆模型Γ-1的误差模型为

E[x,y](t)=H[x](t)+

K[x](t)-S-1[y](t)=

(14)

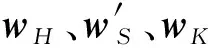
(15)

(16)

(17)

zH0i=0i=0,1,…,nH

(18)

zK0i=0i=0,1,…,nK

(19)

arg min{V(w)}

(20)

式中：

2.3 自适应混合补偿控制方法

自适应滤波器主要包括数字滤波器和自适应算法2部分，数字滤波器通过自适应算法不断调整滤波器的权系数以提高其信号处理的性能。自适应滤波器的结构分为有限脉冲响应(Finite Impulse Response, FIR) 形式与无限脉冲响应(Infinite Impulse Response, IIR) 形式。其中，FIR形式的滤波器只包含零点，具有结构简单、始终稳定且能实现线性相位等特性的优势。FIR自适应横向滤波器的结构原理如图1所示。

为提高系统跟踪精度和抗干扰能力，在MPI逆模型前馈补偿的基础上，基于FIR横向滤波器结构的最小均方差算法(LMS)设计自适应滤波主动控制器。以最小化误差函数为目标，通过修正施加给压电陶瓷作动器的电压信号，以达到对输出信号的精确动态跟踪，如图2所示。图2中：yd(t)为参考输入信号；y(t)为实际系统的输出信号；e(t)为误差信号；xc(t)为经过迟滞蠕变逆模型后转化的电压信号；xf(t)为自适应算法计算得到的反馈电压信号；x(t)为用自适应混合补偿控制方法得到的控制电压输入信号。

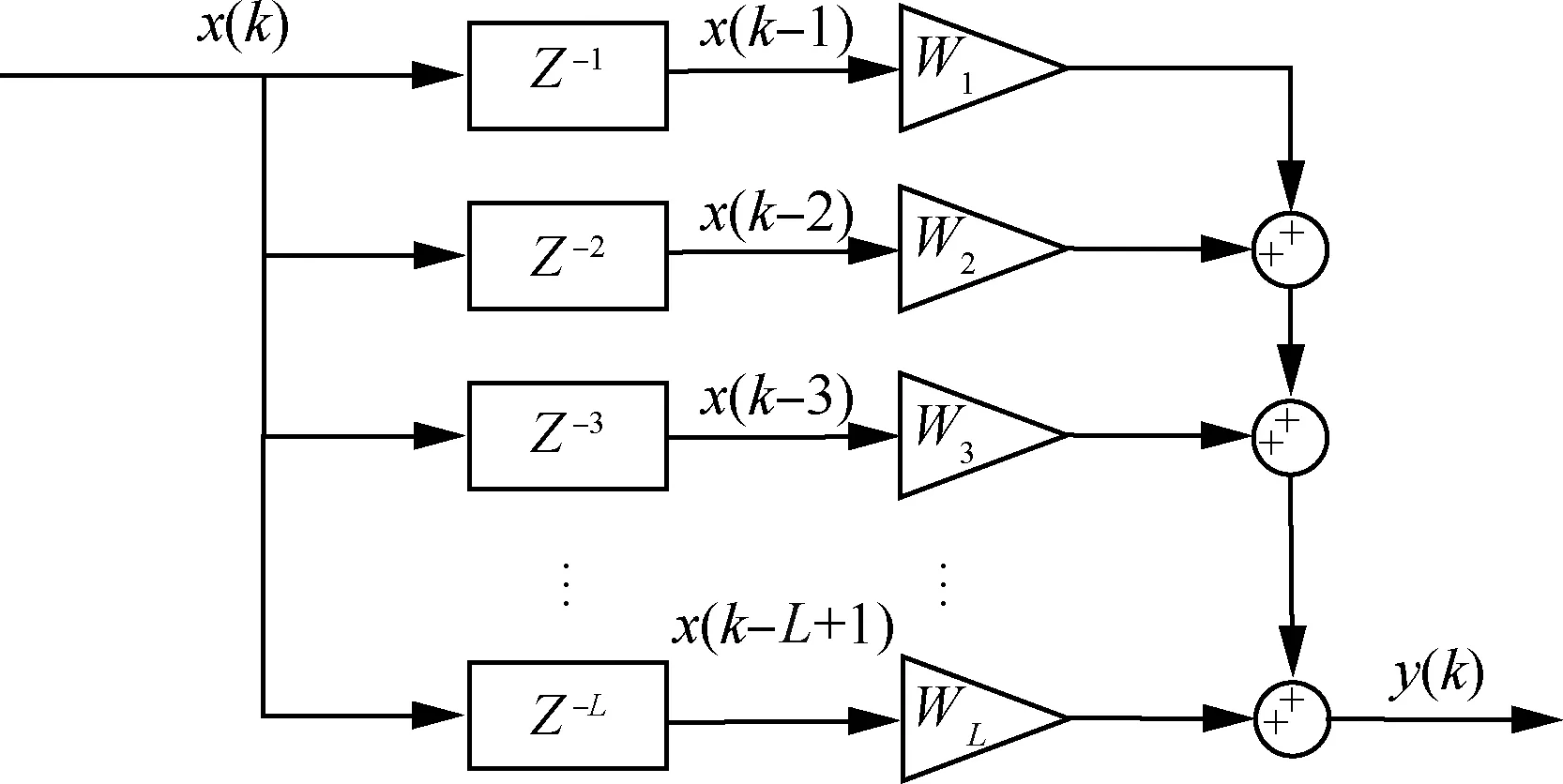
图1 FIR横向滤波器的结构原理图Fig.1 Structure schematic of FIR transversal filter

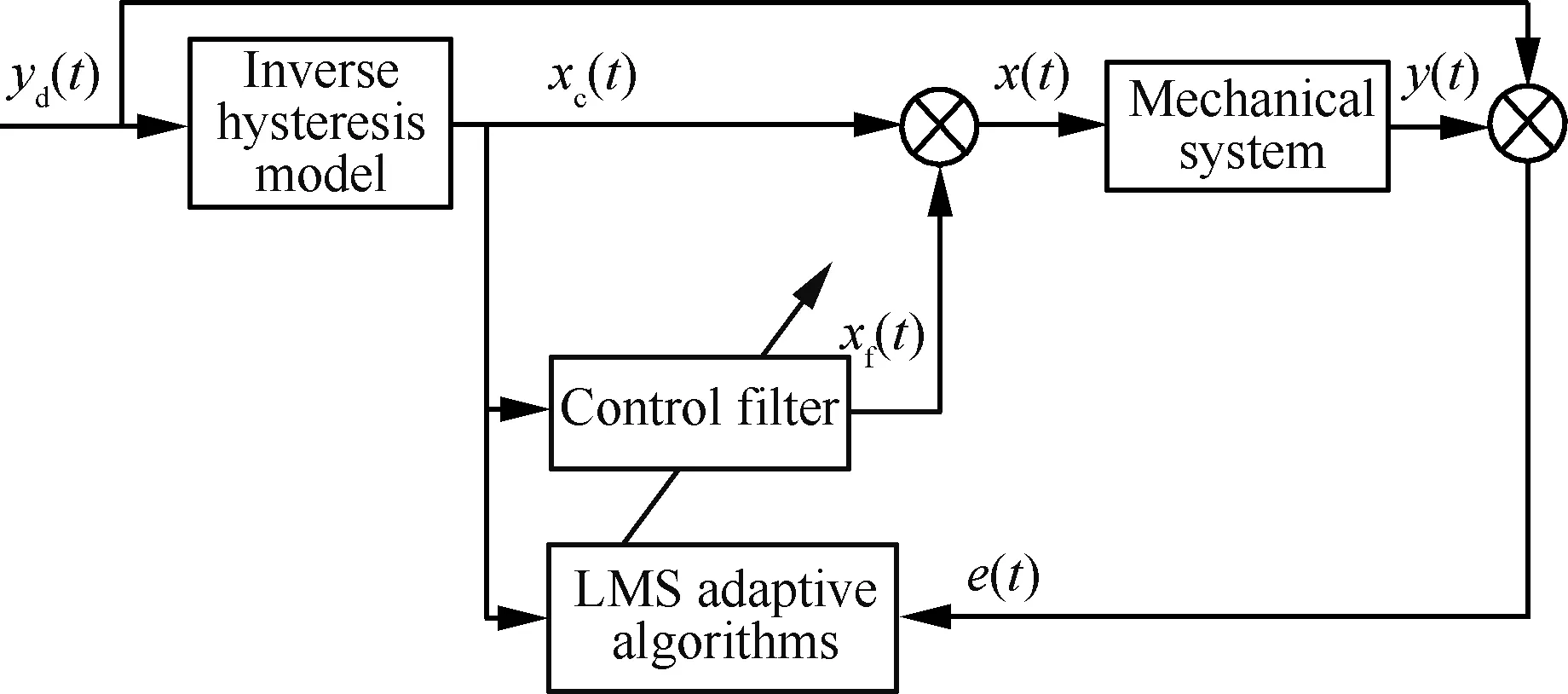
图2 自适应混合补偿控制方法框图Fig.2 Block diagram of adaptive hybrid compensation control method

通过建立自适应滤波反馈控制器，建立了迟滞蠕变逆模型前馈补偿与自适应反馈控制结合的前馈-反馈混合补偿控制方法。前馈补偿在MPI迟滞蠕变辨识模型的基础上，构造迟滞蠕变补偿模块，用来补偿压电陶瓷作动器的非线性特性。利用迟滞输出量与参考信号构造的误差函数建立自适应迟滞反馈补偿控制器。其中，前馈补偿能够快速减弱迟滞特性，而自适应滤波反馈则可以提高补偿控制的动态精度。

3 压电作动器迟滞蠕变补偿控制实验

3.1 迟滞蠕变特性验证实验

实验选用为压电陶瓷叠层作动器，其型号为PITM PICMA P-080.391，其输入电压量程为-20～ 100 V，输出应变量程为-100～800 με。实验采用应变测试手段，沿压电陶瓷叠层作动器轴向粘贴应变片，通过应变信号间接测量压电陶瓷叠层作动器的输出位移，即上文中y(t)为压电陶瓷叠层作动器输出应变值。通过信号发生器产生交变电压，通过压电陶瓷叠层作动器功放放大，施加在作动器上，作动器在逆压电效应作用下发生变形，进而利用应变片测量变形数据，通过动态应变仪以及采集系统进行采集，同时记录驱动电压信号。压电陶瓷叠层作动器迟滞蠕变特性测试与补偿控制系统的实验布置如图3所示。

实验和仿真采用的采样频率为8 192 Hz，MPI模型参数辨识中采用算子个数分别为：nH=10、nK=10、nS=2、m=5。由于压电作动器迟滞非线性表现出记忆性、率相关性等复杂动态特性，因而MPI模型的权系数会随着输入信号的幅值和频率的变化而变化。为了验证不同输入信号下MPI模型对迟滞蠕变曲线模拟的准确性，实验采用的输入信号为x=A[1+sin(2πft)]，其中：A为 输入电压幅值；f为输入电压频率。分别进行输入信号为f=10 Hz,A=50, 80, 100 V，以及A=100 V,f=15, 20 Hz的压电作动器输入输出特性实验。分析对比不同电压幅值和不同电压频率下MPI模型参数辨识结果的仿真精度。

图4给出了输入信号f=10 Hz、A=100 V时的压电作动器电压-应变关系特性曲线。图5给出了输入信号f=10 Hz、A=100 V时MPI模型仿真结果与实验结果的误差，可以看到误差在1%左右，表明MPI模型能够精确地描述压电陶瓷叠层作动器的输出特性。对比图4～图7不同电压频率和幅值下实验测试得到的压电陶瓷叠层作动器输入输出特性曲线，可以看到MPI模型能够对不同驱动电压下压电陶瓷叠层作动器的迟滞蠕变现象作出较为理想的表征，并且具有较好的仿真精度。

图3 压电作动器迟滞蠕变特性测试与补偿控制实验Fig.3 Test of hysteresis characteristics and compensation control experiment of piezoelectric actuator

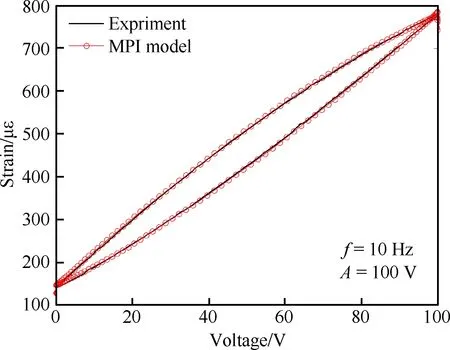
图4 电压-应变关系的仿真与实验对比Fig.4 Comparison of simulation and exprimental voltage-strain relation

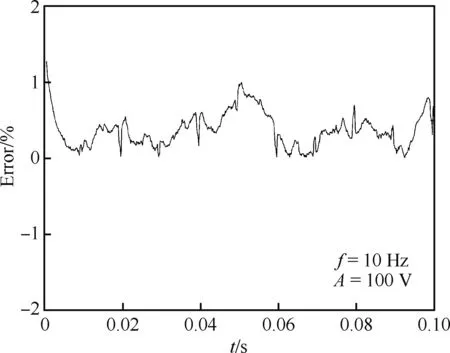
图5 MPI模型仿真结果与实验结果的误差Fig.5 Errors of MPI model simulation and experimental results

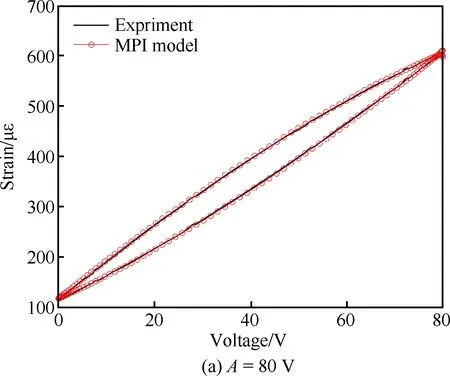
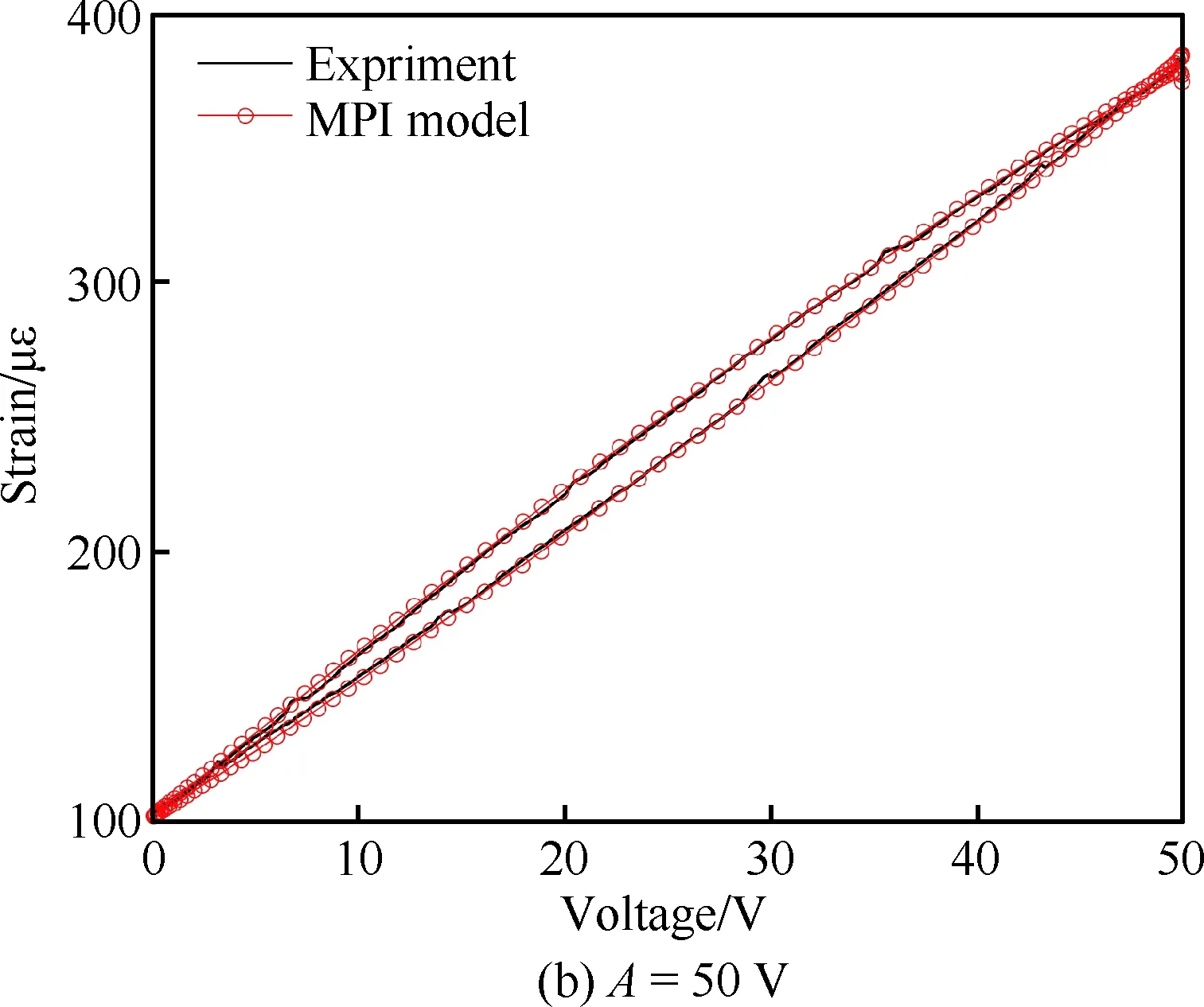
图6 f=10 Hz不同电压幅值下MPI 模型仿真与实验结果对比Fig.6 Comparison of MPI model simulation and experimental results with different voltage amplitudes at f=10 Hz

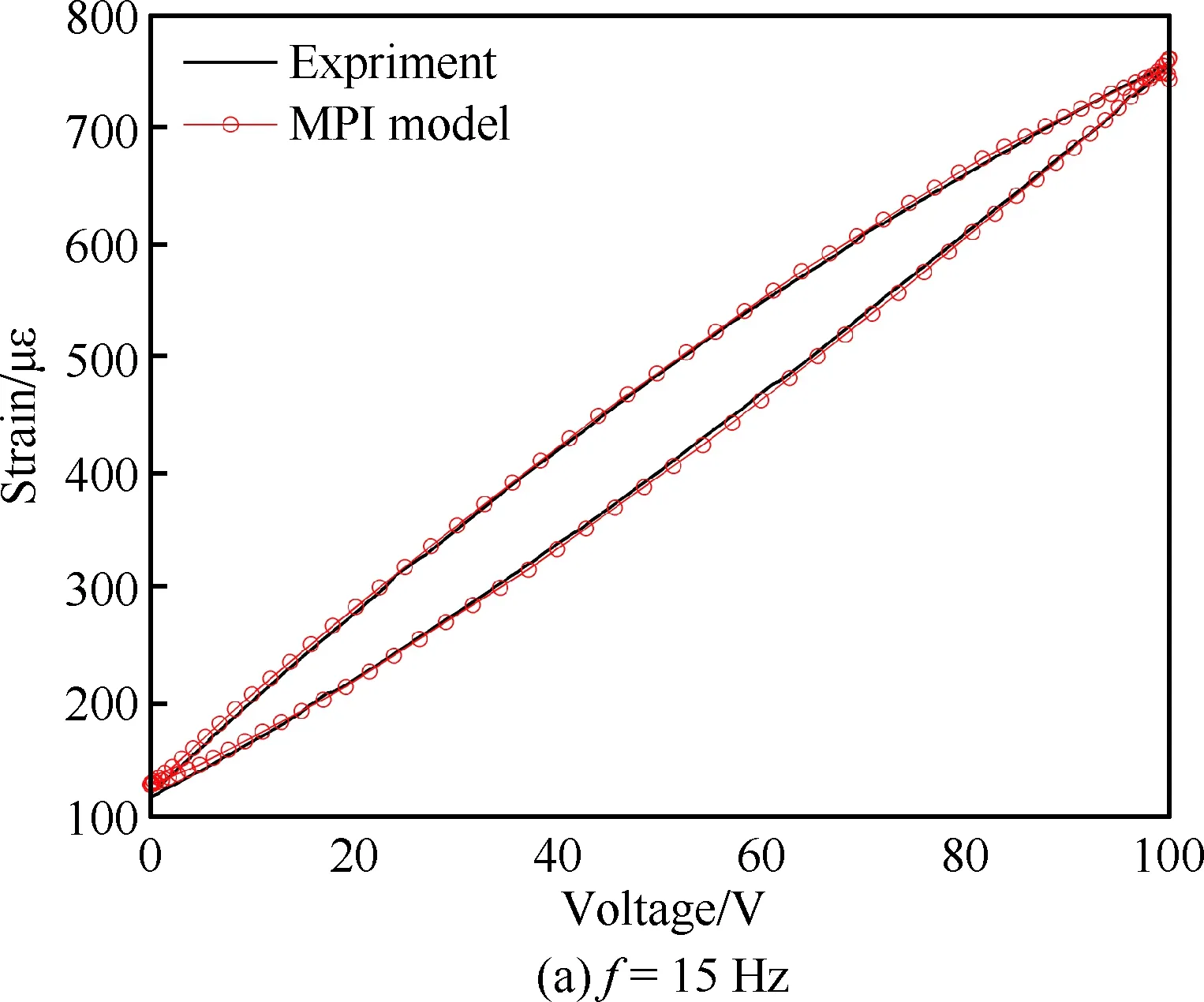
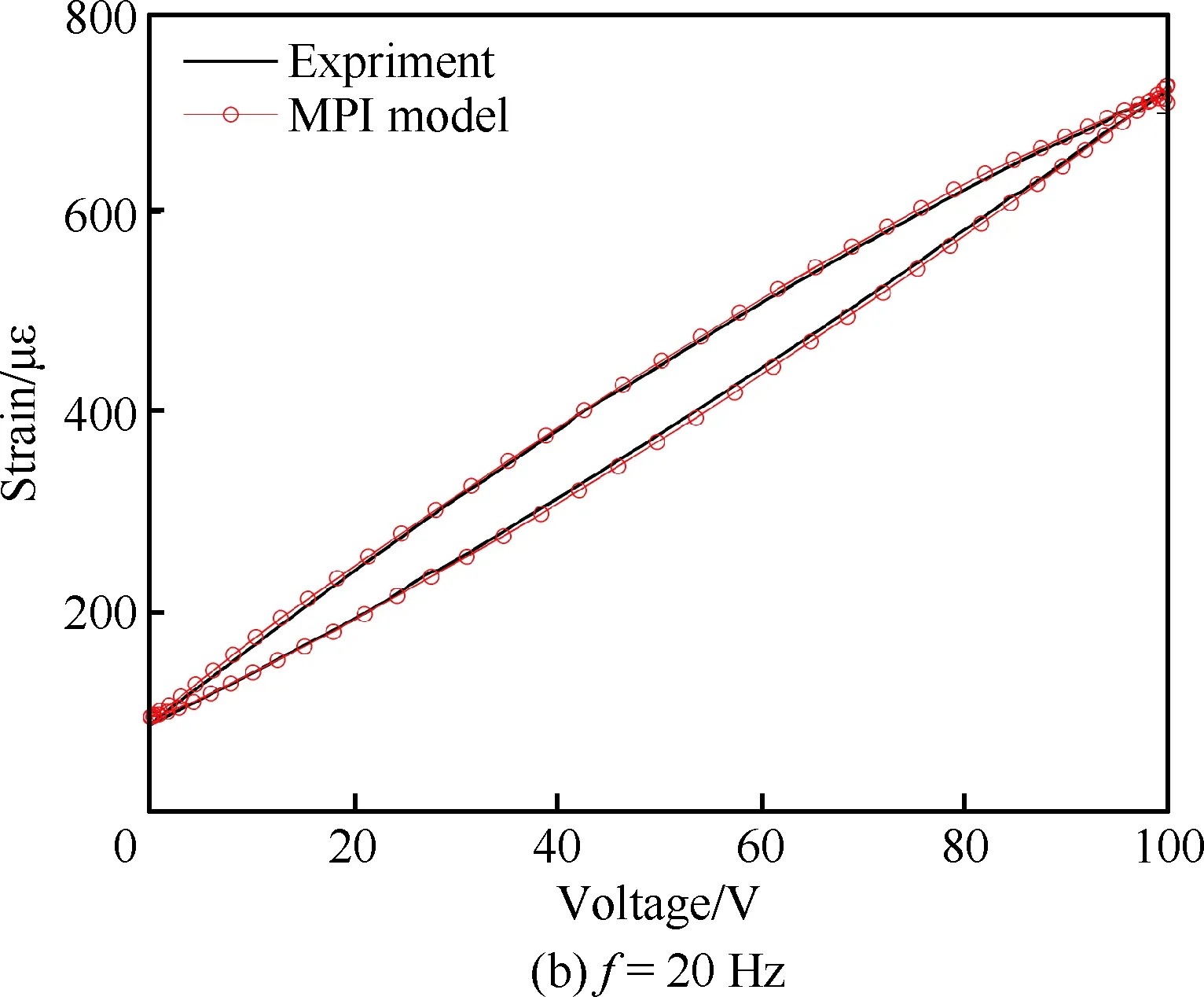
图7 A=100 V不同电压频率下MPI模型 仿真结果与实验结果对比Fig.7 Comparison of MPI model simulation and experimental results with different voltage frequencies at A=100 V

3.2 迟滞蠕变特性自适应补偿控制实验

为验证所设计的自适应混合控制方法的有效性，进行实时跟踪控制实验。在Quanser Real-time控制软件中搭建半实物仿真补偿控制平台，对压电作动器进行迟滞蠕变补偿控制实验，对比前馈补偿与自适应混合控制方法的跟踪精度。实验中采用正弦信号作为参考输入信号，改变参考输入信号的幅值与频率来考察迟滞蠕变补偿器的动态控制效果。

首先给定应变参考信号幅值为100～600 με、频率为10 Hz，进行迟滞蠕变前馈补偿实验。图8为输入电压信号为x=50[1+sin(20πt)]时实验测得的压电作动器输入输出特性曲线。基于该输入信号得到的实验数据，辨识得到MPI模型参数，从而建立MPI迟滞蠕变补偿模型如图9所示。图10 为MPI补偿模型前馈补偿实验结果。从实验结果可以看出，迟滞蠕变前馈补偿器在工作状态下，输出应变与参考信号之间存在较好的线性关系，补偿后的输出应变与参考信号基本相同，压电陶瓷叠层作动器的迟滞蠕变效应得到了有效的补偿。

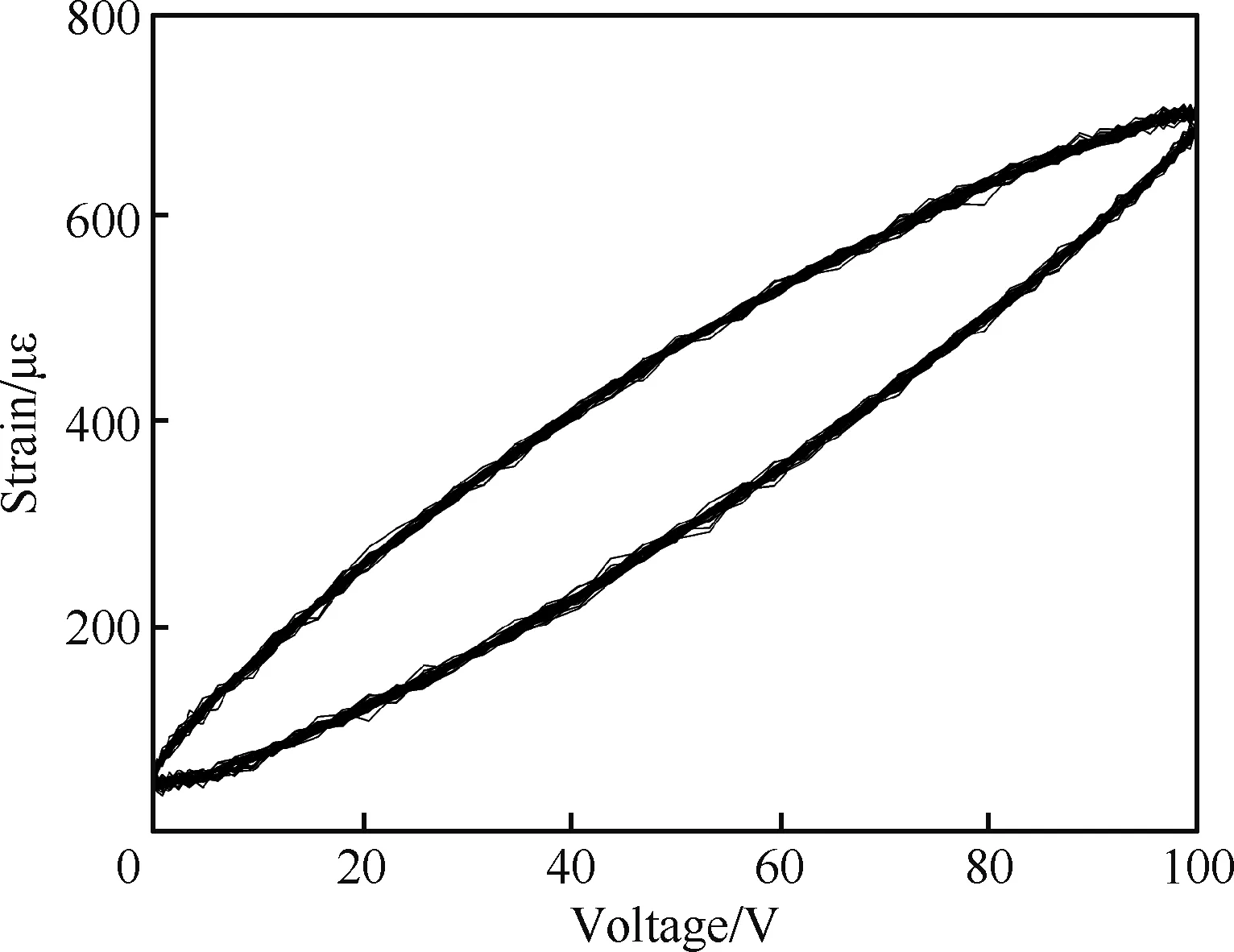
图8 压电作动器电压-应变特性曲线Fig.8 Curve of voltage-strain characteristic for a piezoelectric actuator

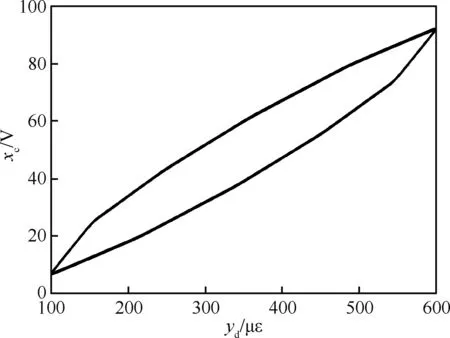
图9 MPI迟滞蠕变补偿模型Fig.9 Compensation model of MPI hysteresis creep

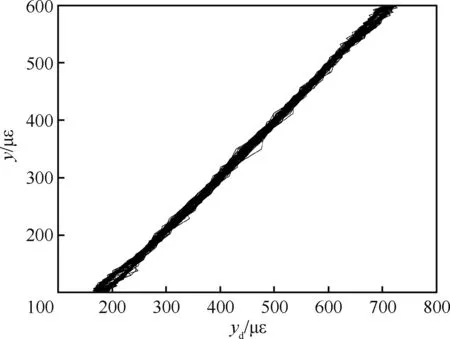
图10 MPI迟滞蠕变模型前馈补偿效果Fig.10 Results of feedforward compensation for MPI hysteresis creep model

其次，改变应变参考信号的幅值与频率进行MPI补偿模型前馈控制与自适应滤波反馈混合控制实验，对比验证自适应混合补偿控制方法的动态补偿跟踪精度。利用图8的输入输出特性曲线数据，建立MPI迟滞蠕变补偿模型搭建前馈补偿控制器。根据前馈补偿误差函数，搭建自适应滤波器进行实时反馈补偿控制。为了验证自适应混合补偿控制方法的自适应性以及动态跟踪性，在压电作动器的量程范围内，进行5组实验：① 应 变参考信号幅值为100～600 με,频率为50 Hz； ② 应变参考信号幅值为100～600 με,频率为20 Hz；③ 应变参考信号幅值为100～600 με,频率为10 Hz；④ 应变参考信号幅值为100～400 με,频率为10 Hz；⑤ 应变参考信号幅值为100～200 με,频率为10 Hz。结果如图11～图15所示。其中，补偿误差定义为从5组实验可以看到，对于压电陶瓷叠层作动器迟滞蠕变非线性的前馈补偿控制，第③组实验前馈控制效果较好(见图13)。随着应变参考信号的输入频率与幅值的变化，前馈控制误差变大。特别的，当应变参考信号幅值变为100～200 με 时，前馈补偿基本失效(见图15)。这是因为前馈补偿模型的控制精度依赖于所建立MPI模型的精度，而MPI模型及其逆模型的权系数随着压电陶瓷作动器输入的频率和幅值的变化而变化，因此MPI迟滞蠕变逆模型前馈补偿方法的动态跟踪性较差。

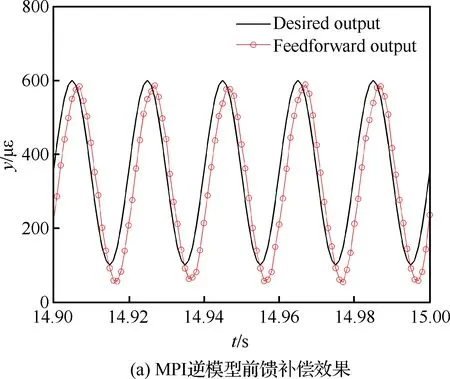
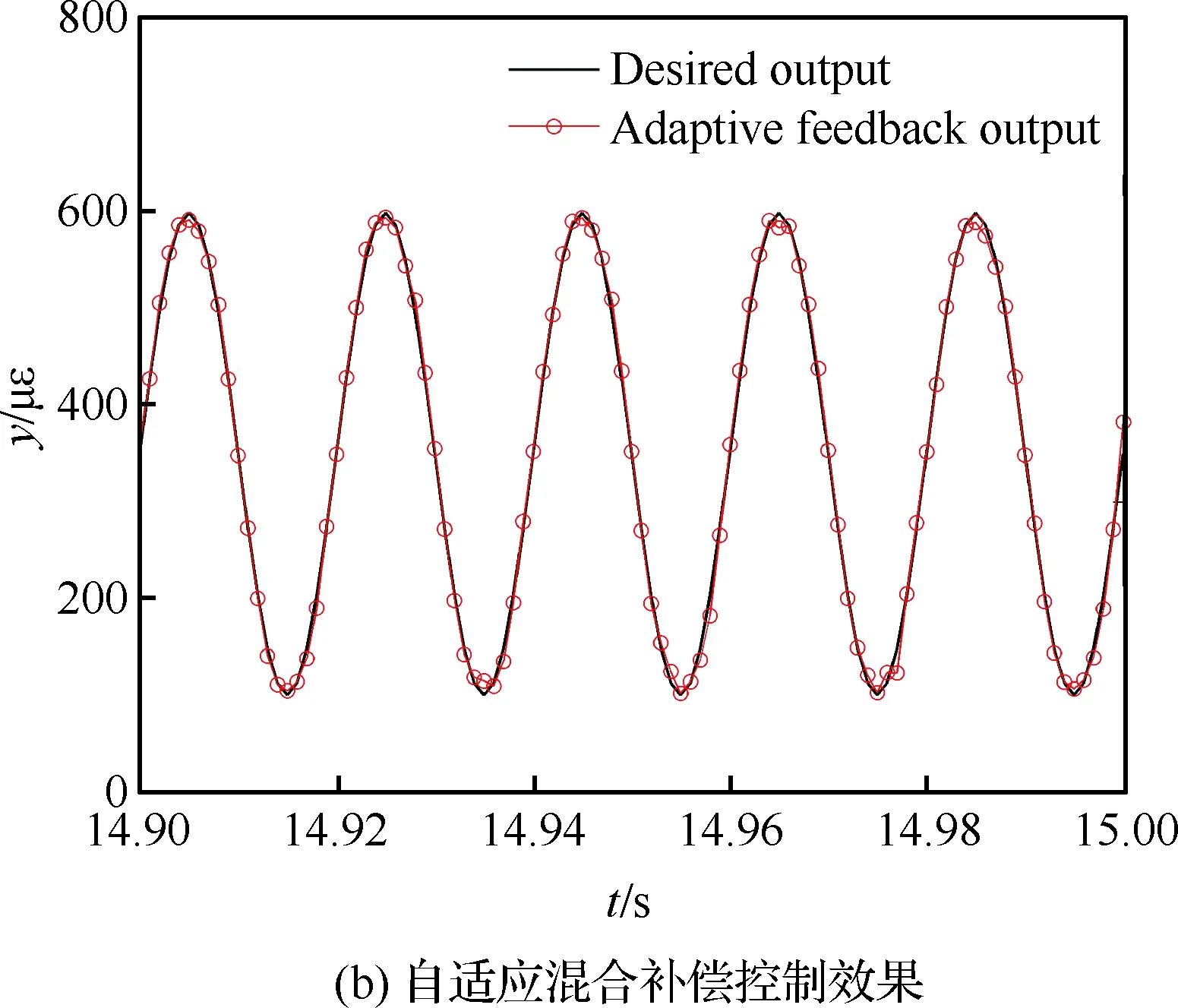
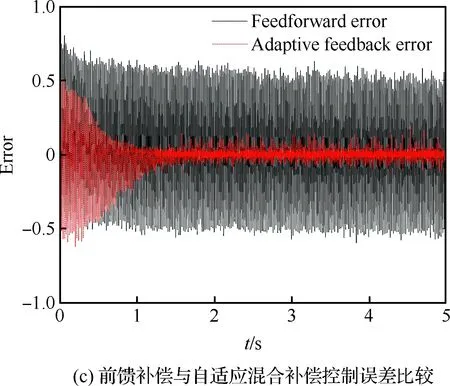
图11 应变参考信号幅值为100～600 με、 频率为50 Hz时的实验结果Fig.11 Experimental results when amplitude is 100～600 με and frequency is 50 Hz of strain reference signal

自适应滤波反馈在其逆模型补偿的基础上，以减小应变参考信号与实际输出信号的误差为目标进行实时动态主动控制，具有收敛性好、计算量小、跟踪能力强的特点。基于LMS设计得到的自适应滤波反馈控制器主要用于受控对象及其参数存在不确定性的情况，当外界环境和工作条件改变时控制器本身的参数或结构也能自动作出相应的变化，以保证系统性能指标都尽可能保持最优。当压电作动器应用于被控结构进行作动时，辨识压电作动器作用于结构时的迟滞蠕变动态特性输入输出数据，建立MPI前馈补偿模型。同时，利用自适应滤波反馈控制器实时调控输入信号进行补偿反馈控制，从而达到实际应用中准确跟踪期望位移以及迟滞非线性补偿精确控制。

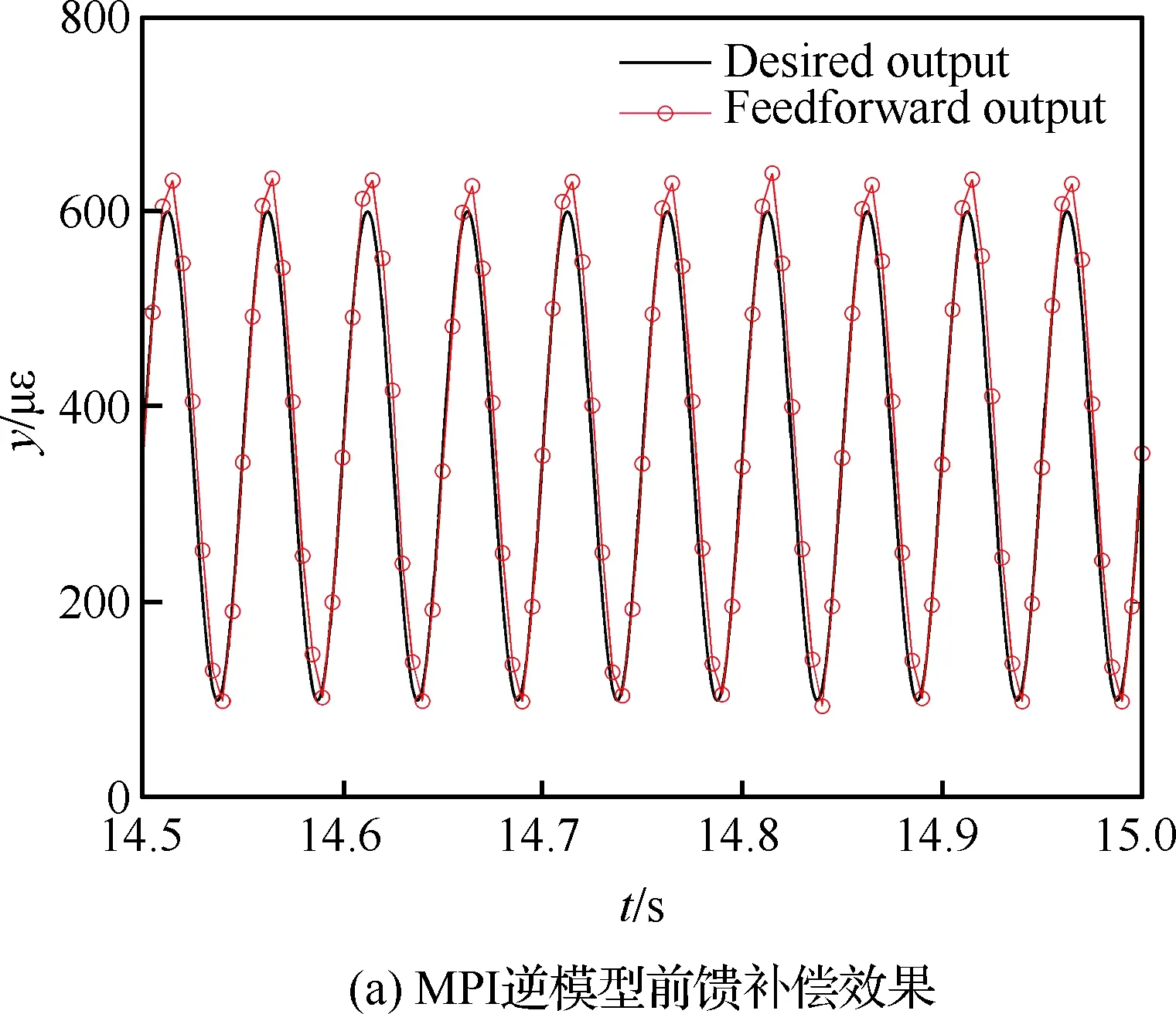
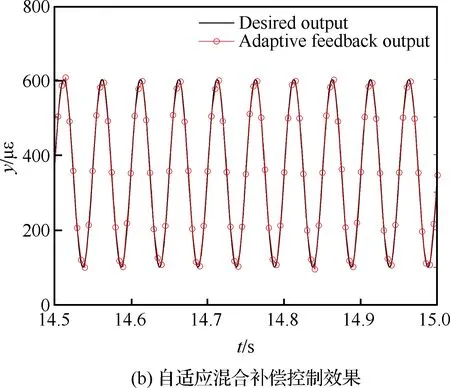
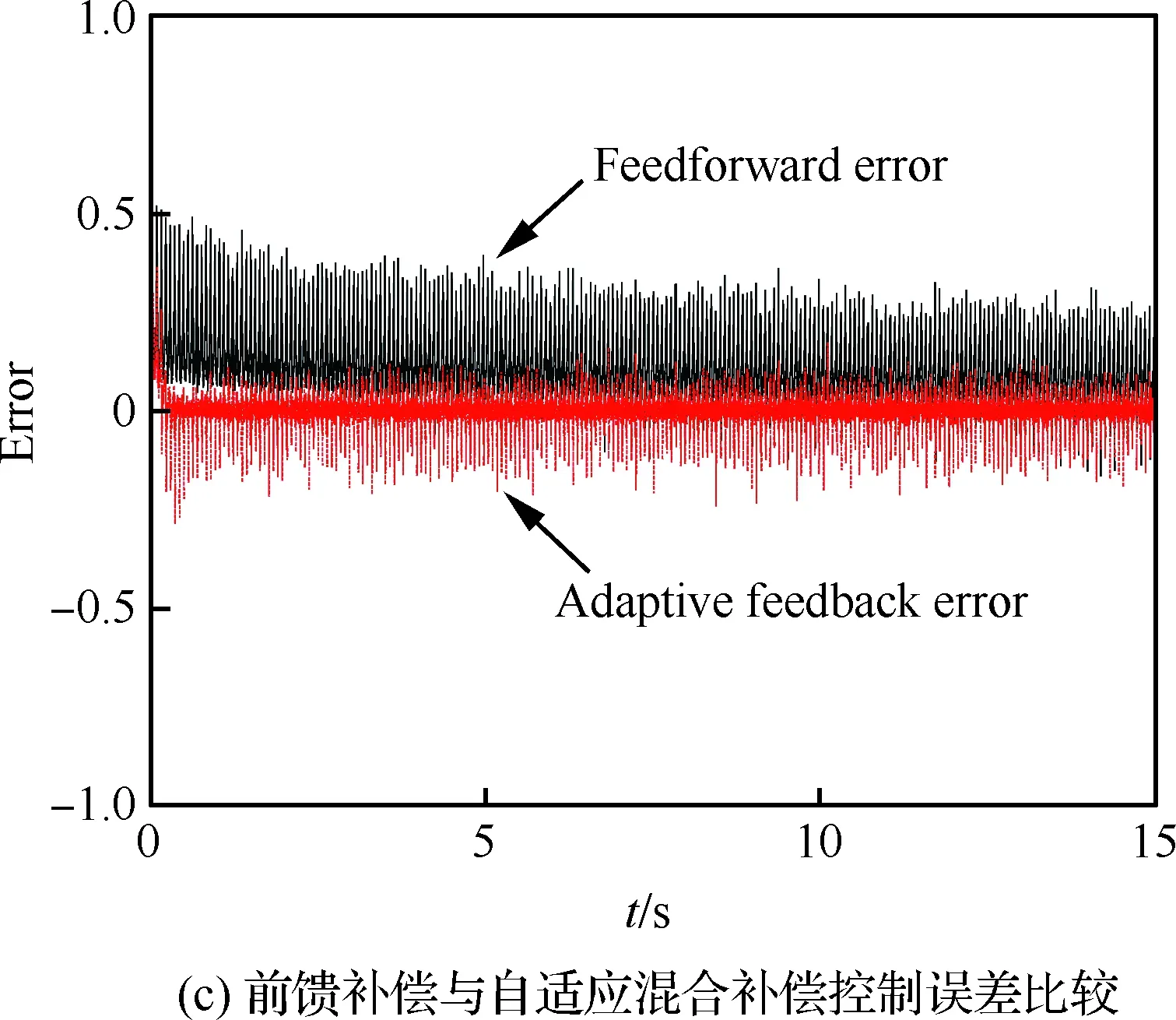
图12 应变参考信号幅值为100～600 με、 频率为20 Hz时的实验结果Fig.12 Experimental results when amplitude is 100～600 με and frequency is 20 Hz of strain reference signal

表1给出在5组实验中，前馈补偿与自适应混合补偿控制的输出信号与给定应变信号在12～15 s 内的平均误差。实验中MPI模型是基于应变参考信号的幅值为100～600 με、f=10 Hz 辨识得到的，从表1可以明显看到当应变参考信号频率增大或其幅值降低时，MPI迟滞蠕变逆模型前馈补偿的平均误差增大了一个量级，此时前馈补偿的效果较差。而自适应混合补偿控制平均误差低于3%。因此，自适应混合补偿控制方法既可以保证补偿模型的精度，又提高了压电作动器非线性的动态跟踪精度以及自适应性。

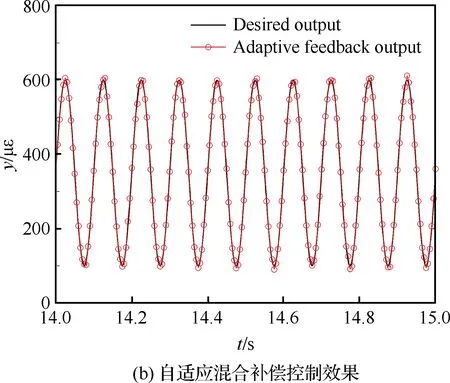
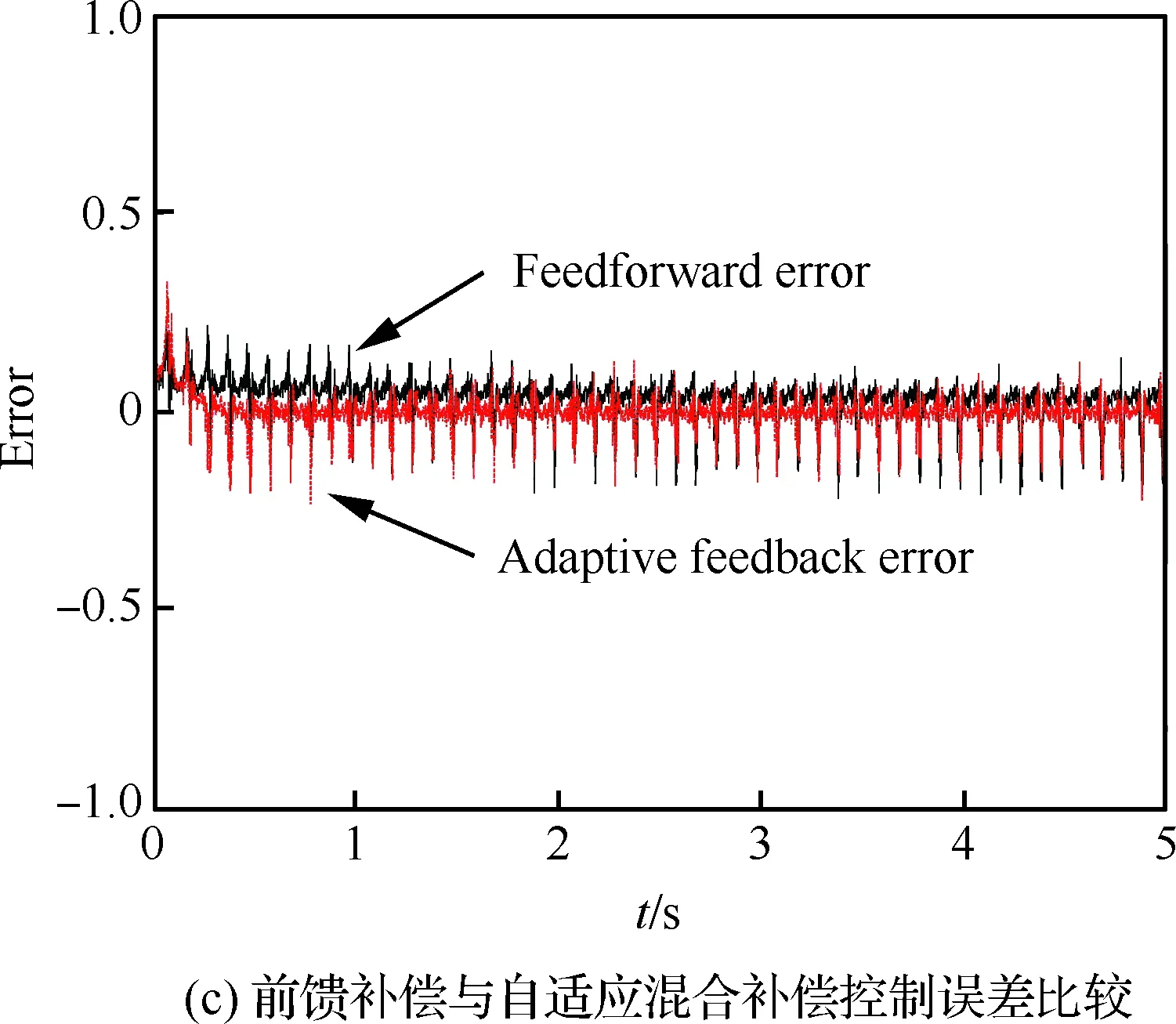
图13 应变参考信号幅值为100～600 με、 频率为10 Hz时的实验结果Fig.13 Experimental results when amplitude is 100～600 με and frequency is 10 Hz of strain reference signal

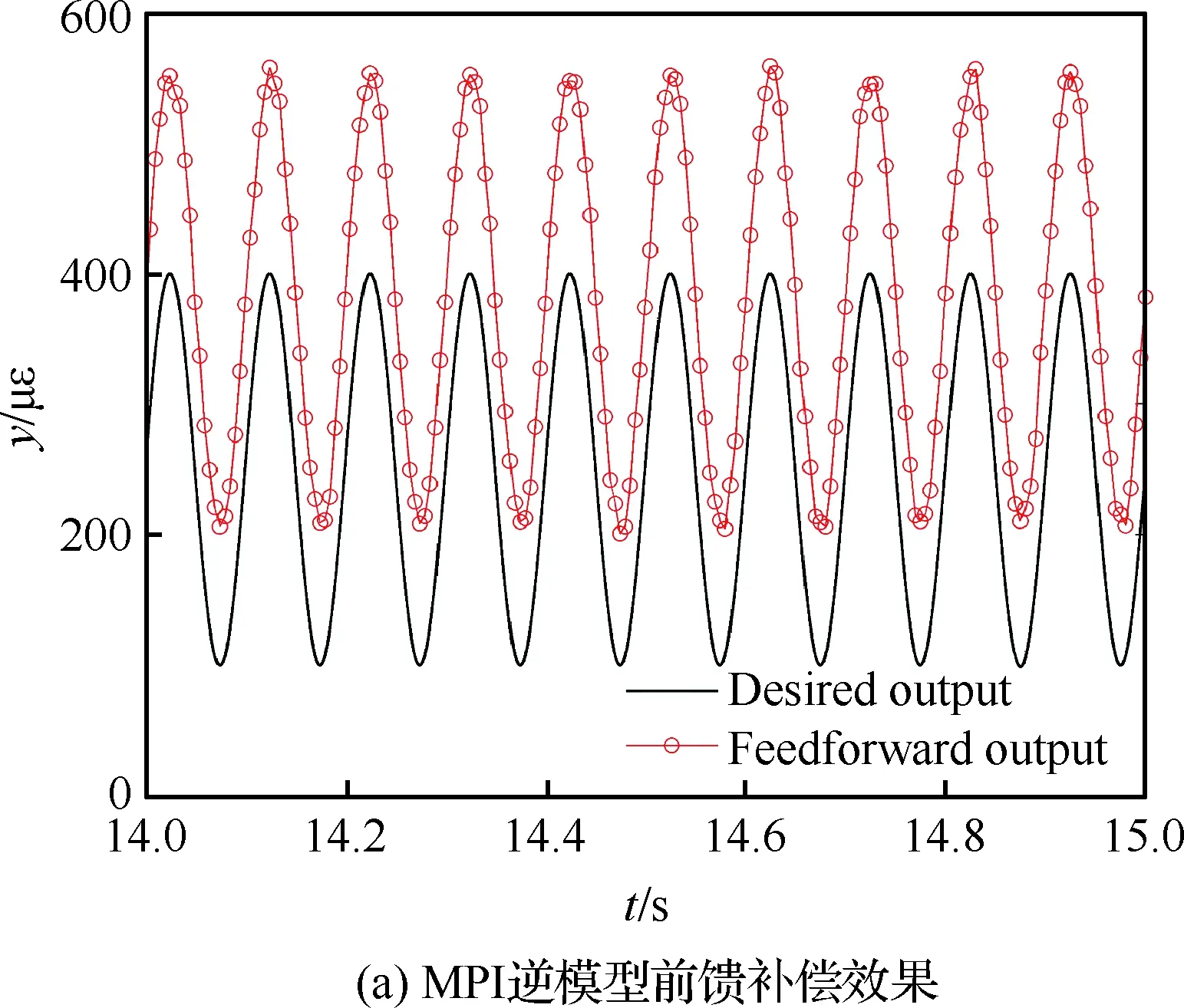
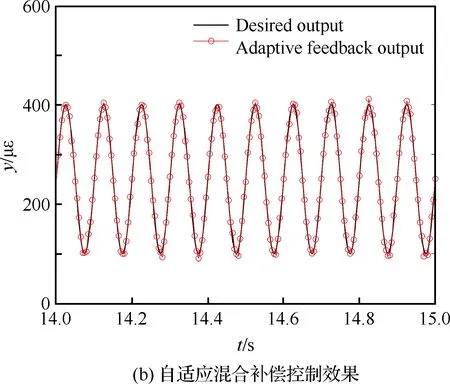
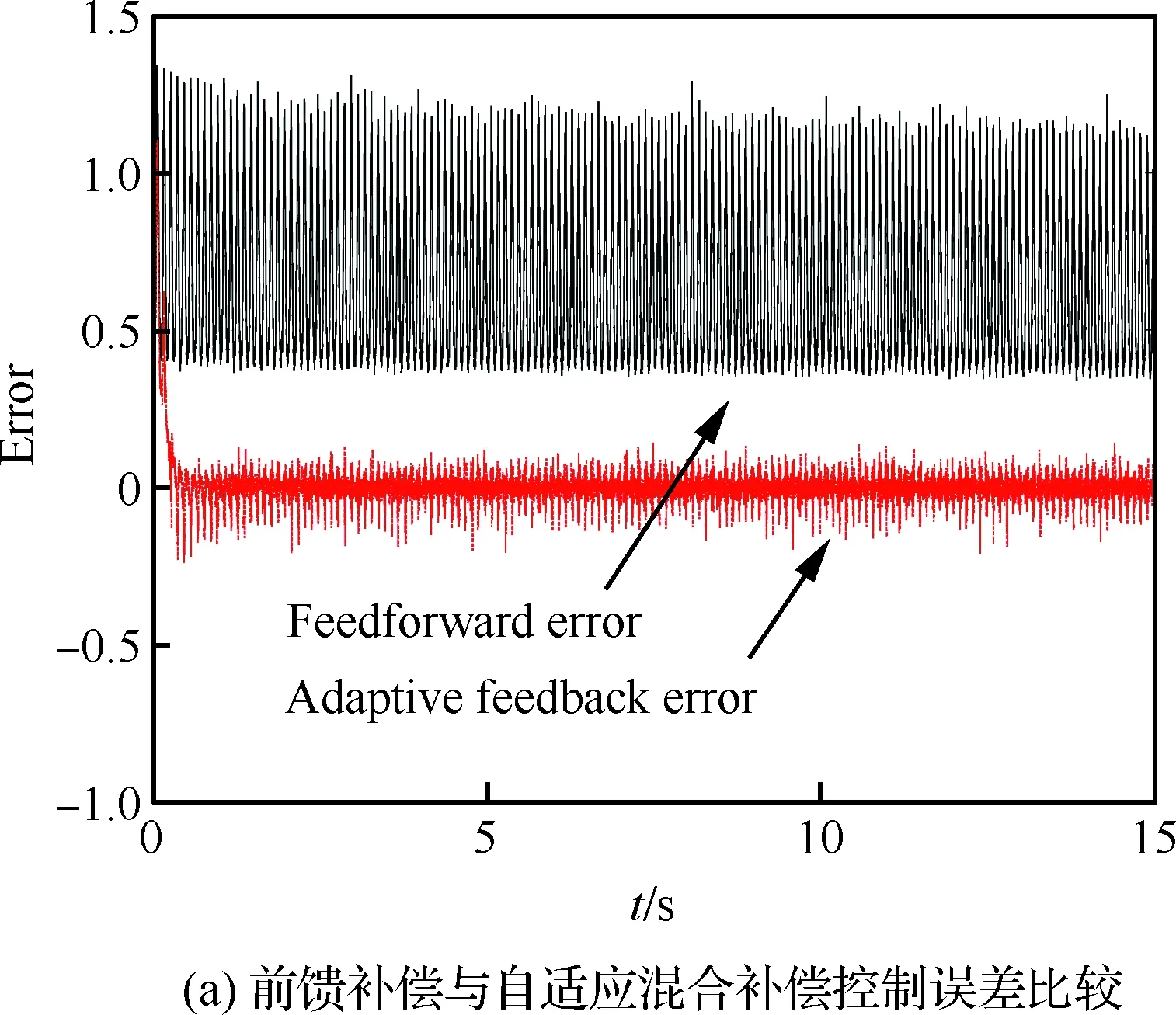
图14 应变参考信号幅值为100～400 με、 频率为10 Hz时的实验结果Fig.14 Experimental results when amplitude is 100～400 με and frequency is 10 Hz of strain reference signal

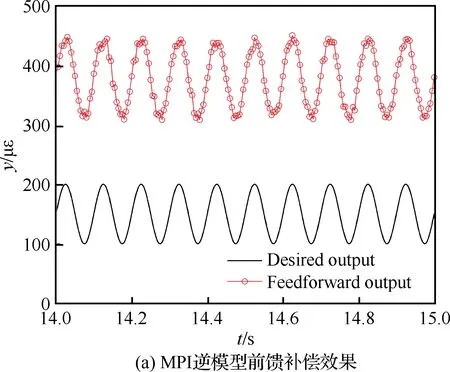
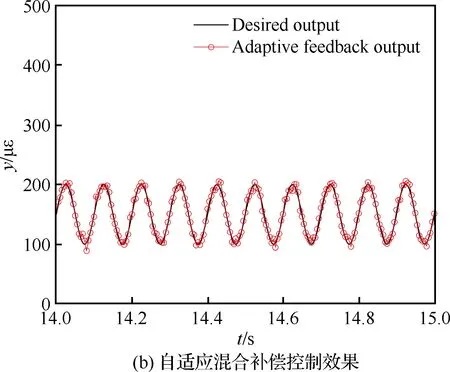
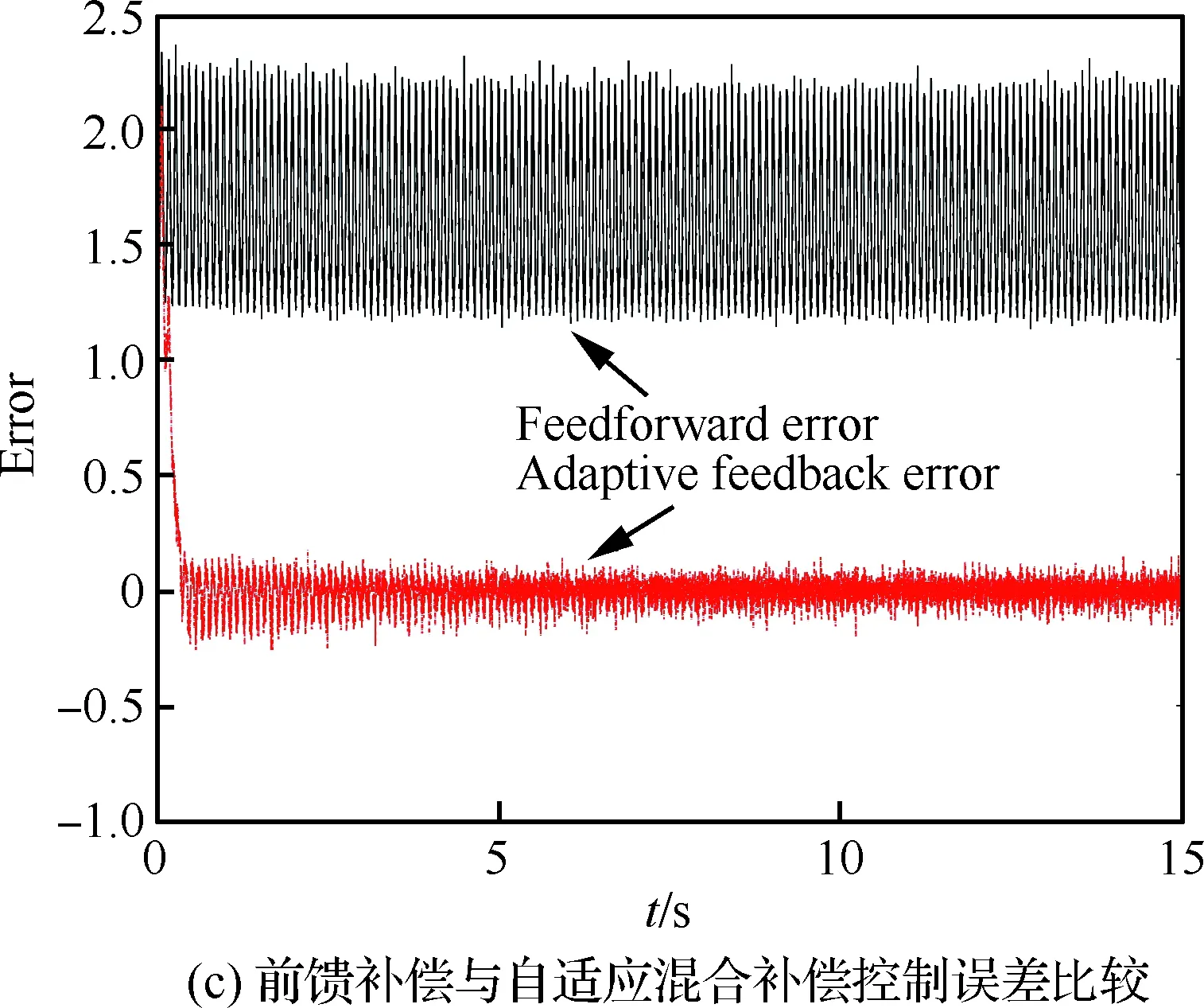
图15 应变参考信号幅值为100～200 με、 频率为10 Hz时的实验结果Fig.15 Experimental results when amplitude is 100～200 με and frequency is 10 Hz of strain reference signal

表1 前馈补偿与自适应混合补偿控制的输出信号与给定应变信号平均误差结果

Table1Averageerrorsofoutputsignalsandgivenstrainsignalsoffeedforwardcompensationandadaptivehybridcompensationcontrol

4 结 论

1) 基于MPI模型同时考虑迟滞特性与蠕变特性对压电陶瓷叠层作动器的非线性进行精细化建模，精确地描述了压电陶瓷叠层作动器迟滞蠕变现象，且具有计算简单、迟滞跟踪能力强的优点。

2) 基于FIR横向滤波器结构的最小均方差算法，设计得到自适应滤波器进行控制反馈。根据前馈补偿误差建立自适应滤波反馈控制器实时调控输入信号，达到准确跟踪期望位移以及迟滞蠕变非线性补偿的精确控制。

3) 搭建MPI补偿模型前馈控制-自适应滤波反馈混合控制器进行实验验证对比，实验结果表明迟滞蠕变前馈补偿与自适应滤波器反馈补偿控制结合的前馈-反馈混合型控制方法可以有效降低迟滞补偿误差，提高压电作动器实时驱动补偿精度，是一种实现压电作动器迟滞蠕变非线性自适应补偿控制的有效方法。