超临界压力下正癸烷在水平矩形冷却通道内的流动传热数值模拟

张卓远，黄世璋，高效伟

大连理工大学 航空航天学院，大连 116024

主动再生冷却技术在超燃冲压发动机热防护中占有非常重要的地位。通常，冷却通道内的压力超过了燃料的临界压力，使得碳氢燃料处于超临界压力状态。超临界压力下，流体的热物理性质随着温度和压力的变化发生非常剧烈的变化，物性的剧变致使浮升力效应增强。考虑浮升力时，超临界压力下流体流动过程和传热现象十分复杂，准确计算超临界压力碳氢燃料的流动传热特性对再生冷却设计至关重要。

超临界压力流体物性变化剧烈这一现象在能源动力、航空航天和核反应堆等领域具有深远的研究价值。国内外对超临界压力二氧化碳和水在考虑浮升力时的流动传热开展了大量实验和数值模拟研究[1-7]。Sharabi等[1]对二氧化碳在超临界压力下方形和三角形截面管的流动传热进行了数值模拟研究。Liu S H等[2]对考虑浮升力时超临界压力二氧化碳在竖直圆管中的换热与流动进行了数值模拟，并且量化分析了浮升力对传热的影响。Liu X等[3]分析了超临界二氧化碳在倾斜螺旋管中流动时，离心力和浮升力对其换热的影响。Licht等[4]探究了Jackson和Seo判别式对于超临界压力水在竖直方管和圆管中流动传热时的适用性。吴刚等[5]发现超临界压力水在倾斜上升管内流动时，由浮升力引起的自然对流会使顶部传热条件恶化，壁面温度高于底部。Sharma等[6]对超临界水在方管中的自然对流和传热开展了实验和数值模拟研究。Lee[7]研究了超临界水在水平矩形管道中流动传热的过程。

热防护技术的飞速发展使得超临界压力碳氢燃料流动换热成为热点问题。与二氧化碳和水相比，一方面，碳氢燃料流经冷却通道会受到很高的热流从而发生裂解、结焦等复杂的化学变化，另一方面，考虑到超燃冲压发动机携带燃料有限，通常冷却通道入口速度较低。这些均会进一步加剧浮升力对传热的影响。程泽源等[8]研究了超临界碳氢燃料在竖直圆管内流动的传热特性，结果表明浮升力效应仅在小质量流量下起作用，且随着圆管直径增大而增强。严俊杰等[9]研究了超临界压力下碳氢燃料在竖直细圆管中对流换热的情形。仲峰泉等[10-12]开展了航空煤油在超临界状态下流动传热的数值模拟研究。Wen等[13]对RP-3航空煤油在超临界压力下水平细圆管内的流动开展了实验和数值模拟研究，结果表明浮升力对换热的影响十分显著。阮波和孟华[14-15]针对碳氢燃料在超临界压力下热裂解和对流换热进行了数值模拟。徐可可[16]对超临界压力航空煤油RP-3水平圆管内的流动与传热进行了数值模拟研究，分析了浮升力在不同入口速度和加热电流下对传热的影响。

然而，现有研究大都采用轴对称圆管模型来探讨浮升力对超临界压力碳氢燃料流动传热特性的影响，基于非对称加热矩形冷却通道的研究鲜有报道。实际上，在浮升力影响较为明显时，考虑到重力加速度和热流的方向性，二者的传热特性和机制有显著的差异，从而引出新的科学问题。本文以正癸烷为研究对象，对其在非对称加热水平矩形冷却通道中的流固耦合传热过程展开数值模拟研究。重点考察了燃烧室不同位置冷却通道中浮升力对传热和热流分配特性的影响及其机理，进一步讨论了考虑浮升力影响时换热经验公式的适用性。该研究为发动机主动再生冷却设计提供重要参考。

1 数值方法

1.1 控制方程

流体区域控制方程为Navier-Stokes方程，本文使用标准k-ε湍流模型，方程具体形式为

(1)

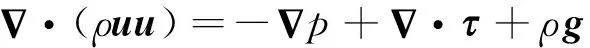
(2)

(3)

(4)

(5)

式中：ρ为流体密度；u为速度；p为流体压力；τ为黏性应力项；g为重力加速度；et为流体总内能；λ为热传导系数；T为温度；k为湍动能；ε为比耗散率；μ为黏性系数；μt为湍流黏性系数；σk和σε为方程湍流普朗特数，其值分别为1.0和1.3；Gk为由时均速度梯度引起的k-ε湍动能生成项；Gb为由浮升力引起的湍动能生成项；C1ε和C2ε为湍流模型常量，其值分别为1.44和1.92；C3ε为模型常量，本文中由于流体流动方向与重力方向垂直，其值取为0。

在式(4)和式(5)中，求解了k-ε湍流模型，并采用了强化壁面的方法，即当计算网格处于近壁面时，求解适用于低雷诺数的方程Wolfstein湍流模型，否则使用壁面函数。

在固体区域求解以下热传导方程：

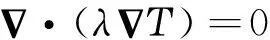
(6)

本文的数值计算中，流-固交界面的温度和热流密度相等。

1.2 计算方法

超临界压力状态下正癸烷的物性随温度和压力的变化而发生剧烈的变化，准确计算其输运和热力学物性十分重要。修正的对比态(Corresponding-state)法[17]是计算流体密度、黏性系数以及热传导系数的普遍方法，计算时采用丙烷作为参考物。正癸烷的定压比热以及内能则采用Soave-Redlich-Kwong(SRK)状态方程计算得到[18]。通过用户自定义函数(UDF)编程将上述物性计算方法与商用计算流体力学软件Fluent相结合，实现碳氢燃料的流动计算。

1.3 算法验证

本文采用的数值模型和计算方法的准确性在之前的研究工作中已经得到了充分的验证[19-23]。本文进一步采用文献[24]中的实验数据与考虑浮升力时的计算结果进行对比，计算工况如表1所示，表中Tin、pin和uin分别为入口温度、入口压力和入口速度，qs为加热段热流密度。结果如图1所示，图中横坐标x/D为加热段的无量纲坐标，D为水力直径，纵坐标Tw为内壁面温度，exp和cal分别表示实验与计算结果。由于浮升力的影响，下壁面温度低于上壁面，计算结果与实验测量结果非常吻合。结果表明，本文的数值模型能够准确预测水平管内浮升力对超临界压力流体流动和传热过程的影响。

表1 验证模型工况Table 1 Operation conditions of validation model

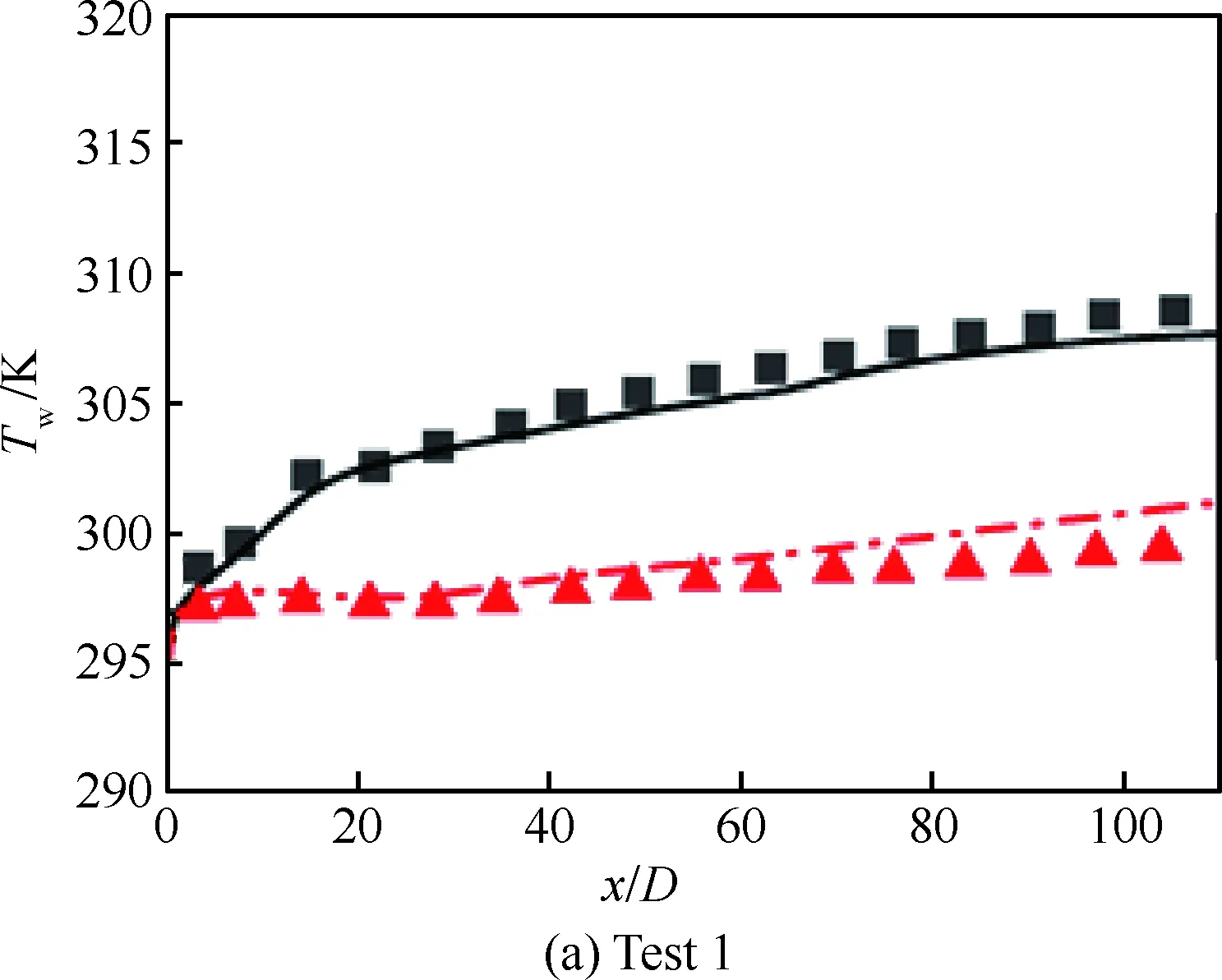
图1 水平圆管模型验证结果Fig.1 Validation results of a horizontal circular tube model

2 计算模型

超燃冲压发动机燃烧室及其冷却结构如图2(a) 所示。矩形燃烧室内的高温燃气对四周壁面进行加热，高温热流通过壁面进入冷却面板中，冷却面板由冷却通道依次排列而成。图2(a)中所示发动机处于水平匀速飞行状态，重力加速度g的方向垂直向下。

单个发动机冷却通道示意图如图2(b)所示。冷却通道内外截面均为正方形，内截面边长L=2 mm， 壁厚为0.5 mm。固体区域材料导热系数取为λ=20 W/(m·K)。入口段为150 mm，用来保证湍流流动充分发展；出口段为150 mm，用来减少出口边界条件对碳氢燃料流动的影响；中间加热段长度取为500 mm，上壁面外侧施加均匀的热流密度。不失一般性，图2(a)给出了3个位于冷却面板不同位置处的冷却通道受热方向和重力加速度方向的示意图。为方便比较不同位置冷却通道的传热特性，将燃烧室上侧和左侧冷却通道旋转，加热面均置于上方。旋转后的模型重力加速度方向如图2(c)所示。以Case A、Case B和Case C分别表示燃烧室上侧、下侧和左侧位置处的冷却通道，各计算模型和相应工况见表2(表中g为重力加速度的大小)。其中，冷却通道在燃烧室中所处的位置与图2(a)对应。值得注意的是，不考虑浮升力影响时，换热过程与冷却通道位置无关。

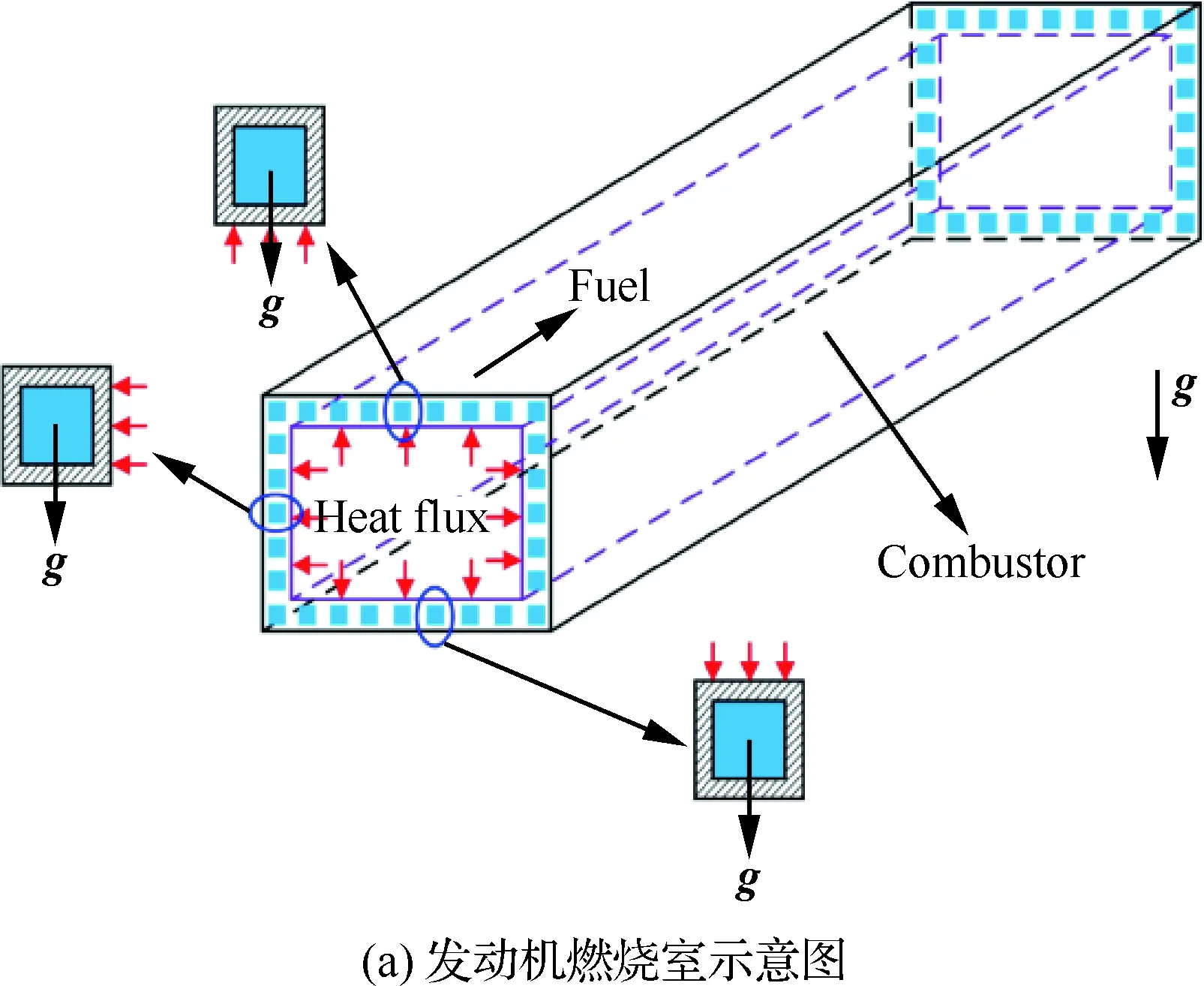
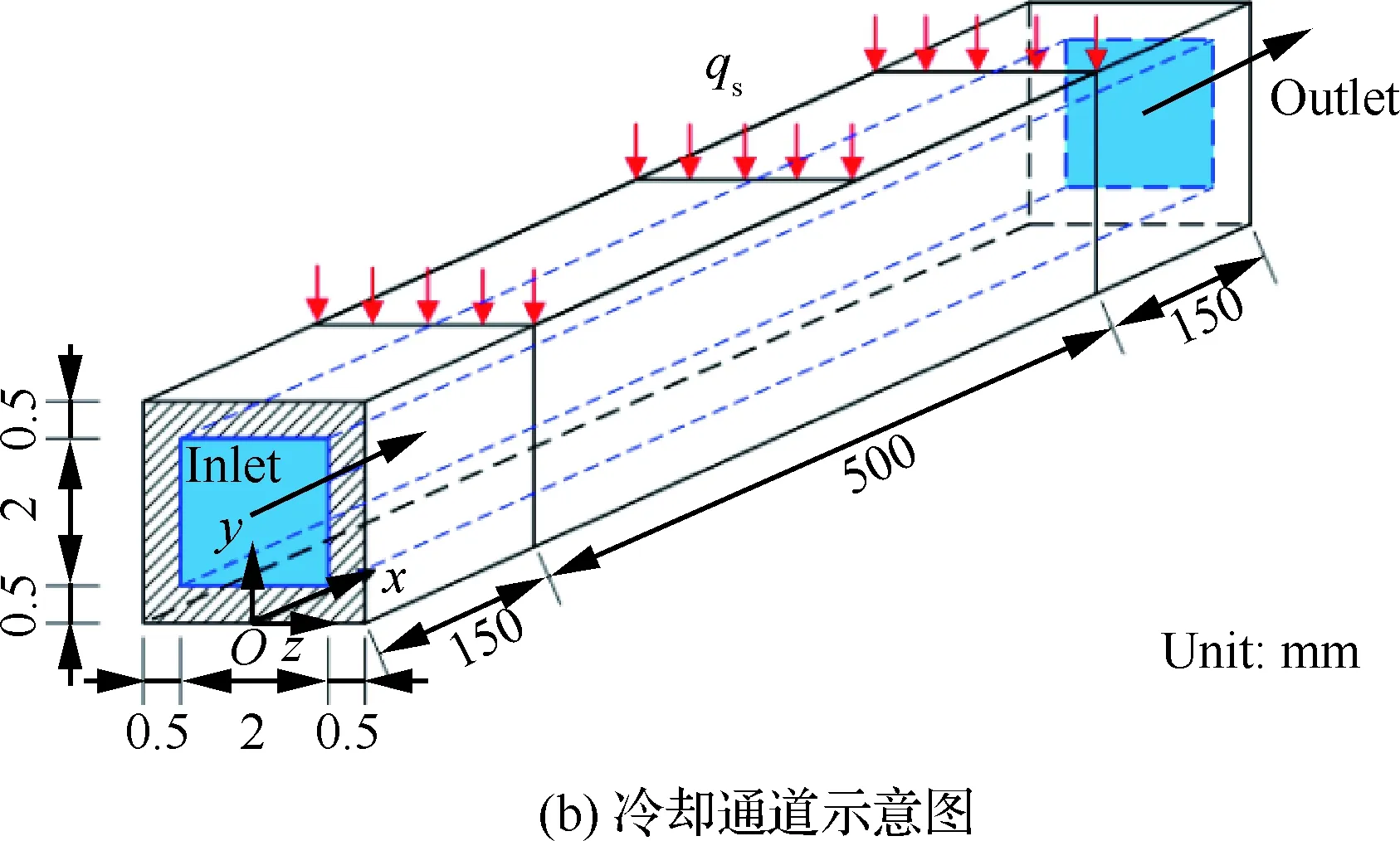
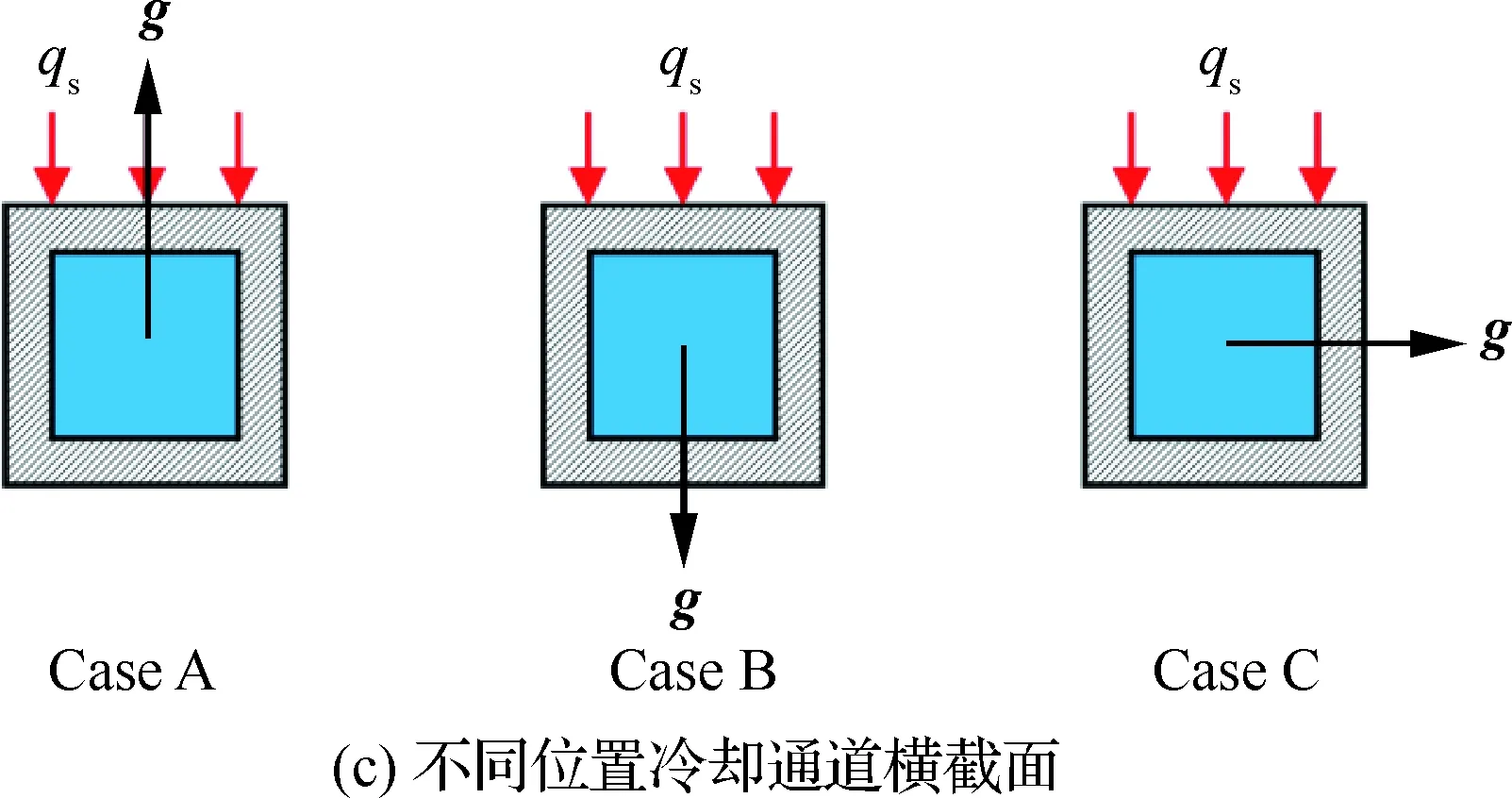
图2 发动机燃烧室及冷却通道示意图Fig.2 Schematic of engine combustor and cooling channel

除燃烧室左侧冷却通道外，其余计算模型均关于Oxy面对称，为提高计算效率，取冷却通道的一半进行数值模拟研究。对计算模型进行网格无关性验证后确定x、y、z方向的网格数量为1 050×110×110，固体区域划分了15层网格，其中Case A、Case B由于对称性，z方向网格数量可以只取为一半即55。壁面处第1层网格满足y+≤1，并且前3层网格满足y+≤5，这样可以确保近壁面流场的计算精度，避免壁面函数可能带来的计算误差。

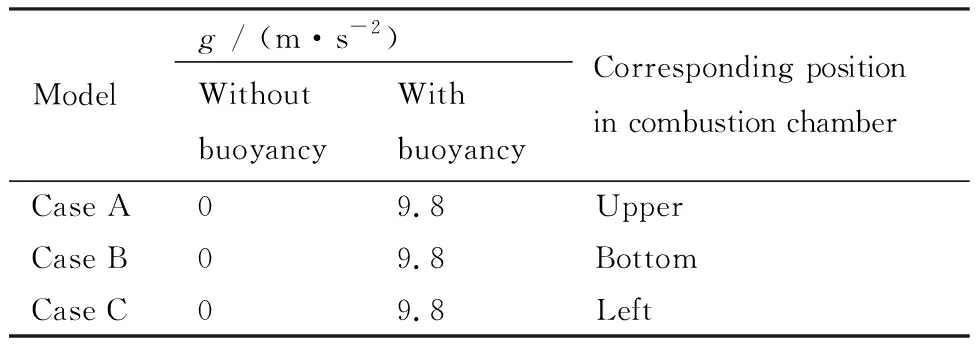
表2 计算模型Table 2 Computational models

3 浮升力对换热特性的影响及其机理

考虑浮升力影响时，超燃冲压发动机燃烧室(图2(a)所示)不同位置所受的热/力载荷存在明显差异，载荷的差异会直接影响流动换热过程。本节探讨浮升力对超临界压力正癸烷在不同位置水平方形冷却通道内流动传热的影响。

计算时，工作压力为5 MPa，入口速度为0.6 m/s， 入口温度为300 K，加热段壁面热流密度为1 MW/m2。3种工况如图2(c)所示，均与不考虑浮升力作对比。不考虑浮升力时流动传热与位置无关，此时Case A、Case B和Case C为同一种情况，只计算一次。

3.1 燃烧室上侧冷却通道

燃烧室上侧冷却通道对应的计算模型为Case A，该工况下重力方向为+y。通过与不考虑浮升力影响的计算结果进行对比，研究浮升力对传热过程的影响。

流体平均温度的计算表达式为

(7)

式中：cp为流体区域的定压比热；A为积分面域；dA为面微分向量。

图3给出了流体平均温度Tb沿x方向的变化情况，图中W/O buoyancy表示不考虑浮升力时的情形。结果显示，浮升力对流体平均温度的影响非常微弱，可以忽略不计。实际上，流体平均温度只受到能量守恒方程的影响，不会受到浮升力的影响。图4显示了Case A内壁面平均温度沿流动方向的变化情况，图中纵坐标Tw表示内壁面平均温度(变量沿z方向平均)，Twu、Tws、Twb分别表示上壁面、侧壁面和下壁面的平均温度。加热初始段，温度迅速升高，流动后半段，速度增大，强迫对流换热效果增强，浮升力对传热的影响减弱，内壁面温度曲线基本重合。与不考虑浮升力的结果相比，上壁面温度最多降低20 K。侧壁面温度变化较小，受浮升力的影响较弱。下壁面温度相较于不考虑浮升力时最多升高约25 K。

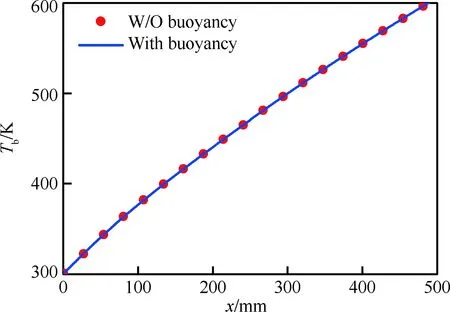
图3 流体平均温度沿x方向的变化Fig.3 Variations of averaged fluid temperature along x direction

图4 Case A内壁面平均温度沿x方向的变化 Fig.4 Variations of averaged interior surface temperature along x direction for Case A

冷却通道壁面温度分布与热流分配特性的变化过程紧密相关，两者共同影响冷却通道各壁面的对流换热能力。发动机燃烧室壁面受到燃烧室内高温燃气的加热，冷却通道仅在单面进行加热。实际上，固体区域的耦合导热作用会对热流进行再分配。冷却通道流固耦合传热过程中，加热面(上壁面)外侧施加的热流主要分成3部分分别进入冷却通道。首先，部分热流直接从冷却通道的上壁面内侧对燃料进行加热；其次，部分热流迅速通过冷却通道固体区域向下传递，其中一部分由侧壁面内侧传入冷却通道内；最后，部分热流则通过下壁面内侧进入冷却通道。

热流被重新分配后，冷却通道各壁面平均热流密度沿流向的变化如图5所示,图中纵坐标qw表示内壁面平均热流密度，qwu、qws和qwb分别表示上壁面、侧壁面和下壁面的平均热流密度。结果表明，与不考虑浮升力相比较，上壁面内侧的热流密度增加9.8%，下壁面内侧热流密度减少15.8%， 浮升力对于侧壁面热流密度影响较小。可以看出，浮升力使得冷却通道内的热流分配特性发生明显变化。

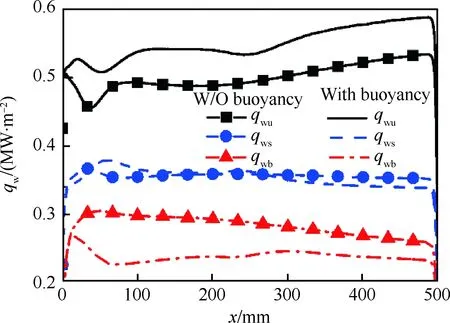
图5 Case A内壁面平均热流密度的变化Fig.5 Variations of averaged interior surface heat fluxes for Case A

为了说明浮升力对冷却通道温度分布和热流密度在固体壁面再分配的影响，下文通过由浮升力引起的二次流动进一步阐述冷却通道温度变化以及热流密度再分配的形成机理。

超临界压力下流体的物性随温度的变化非常剧烈，其中密度在拟临界温度附近随温度的增加急剧下降。因此，冷却通道中流体温度分层会导致密度呈现出严重的不均匀性。图6给出了不考虑浮升力和考虑浮升力时Case A在x=0.2，0.4，0.6 m横截面处的密度分布。由图6可知，流体区域形成了明显的密度分层。在浮升力的作用下，中心区域的低温高密度流体由中心区域向上流动，同时靠近壁面的高温低密度流体沿着侧壁面向下流动，从而形成垂直于流动方向的二次流动。图7显示了冷却通道不同截面处由浮升力引起的二次流动以及流线分布(图中uy为y方向的速度分量)。由于浮升力的作用，中心区域的低温流体不断向上壁面流动，使得上壁面传热出现强化，温度降低，如图4所示。冷却通道下壁面附近积聚了大量高温低密度流体，换热能力明显下降，温度升高。同时，由于上壁面内侧换热能力提升，热流在重新分配时主要往上壁面集中，下壁面分配的热流明显降低，如图5所示。

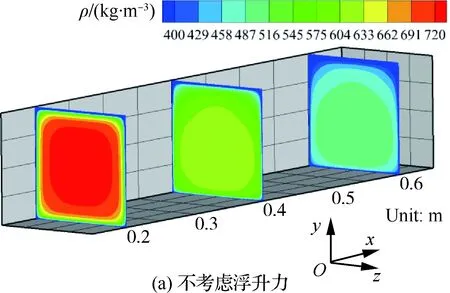
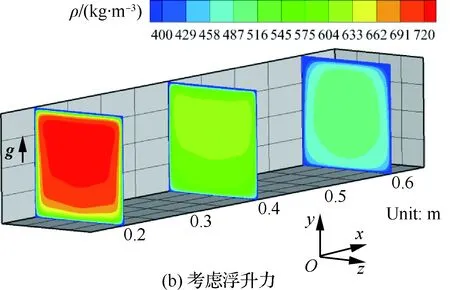
图6 Case A不同横截面密度分布Fig.6 Distributions of density at different cross-sections for Case A

为了定量评价浮升力对冷却通道各壁面对流换热能力的影响，本文引入对流换热系数，其计算表达式为

(8)

图8给出了冷却通道各壁面对流换热系数沿流向的变化情况，图中hcu、hcs和hcb分别表示上壁面、侧壁面以及下壁面的对流换热系数。由于浮升力的影响，上壁面平均对流换热系数增加约12.2%，侧壁面和下壁面平均对流换热系数分别减小约2.5%和20.0%，对流换热能力降低。

图7 Case A不同横截面的二次流动Fig.7 Secondary flow at different cross-sections for Case A

图8 Case A内壁面平均对流换 热系数沿x方向的变化Fig.8 Variations of averaged convective heat transfer coefficients at interior surfaces along x direction for Case A

3.2 燃烧室下侧冷却通道

燃烧室下侧冷却通道的计算模型为Case B，该工况的重力加速度g沿-y方向，继续选择不考虑浮升力的计算结果进行对比。

图9给出了Case B各内壁面平均温度沿流向的变化情况。该工况下，浮升力使冷却通道各壁面的平均温度均有所降低。下壁面温度降低最明显，最多降低约50 K。侧壁面温度最多降低约45 K，上壁面温度最多降低约33 K。

重力加速度方向改变后，冷却通道的热流分配特性也发生了变化。图10为Case B各内壁面平均热流密度沿流向的变化情况。与不考虑浮升力的情况相比，上壁面平均热流密度降低11.1%，而侧壁面和下壁面内侧平均热流密度分别升高7.0%和2.2%。

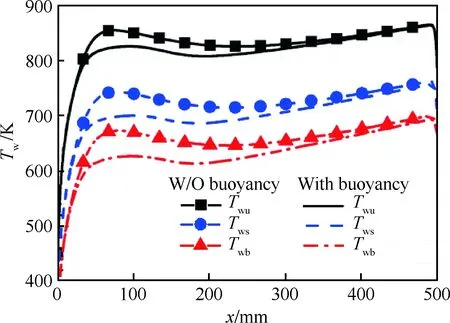
图9 Case B内壁面平均温度沿x方向的变化Fig.9 Variations of averaged interior surface temperature along x direction for Case B

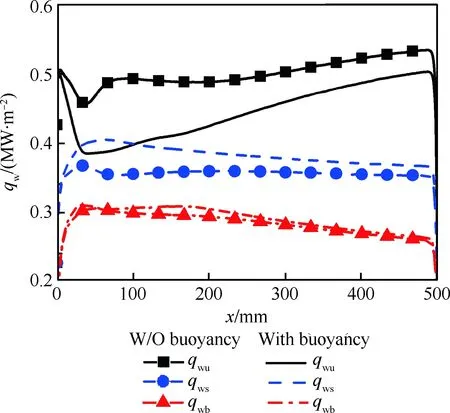
图10 Case B内壁面平均热流密度的变化Fig.10 Variations of averaged interior surface heat fluxes for Case B

图11给出了考虑浮升力影响时Case B不同横截面上y方向的速度分量和二次流动的流线，图12为考虑浮升力时Case B不同横截面的密度分布。比较图6(a)和图12可知，由于浮升力的作用，中心区域的低温高密度流体沿-y方向朝冷却通道下壁面流动，使下壁面的换热能力得到显著提升，温度明显降低，如图9所示。壁面温度降低使得热流分配时下壁面内侧的热流密度增加。同时，由流线图可以看出冷却通道侧壁面附近的高温低密度流体沿着壁面向上流动，因此冷却通道侧壁面附近流体存在较大的y方向速度分量。该处二次流动使冷却通道侧壁面的换热能力增强，温度降低，相应的热流密度增加。冷却通道上壁面附近汇聚了大量高温低密度流体，且流动方向偏离壁面，因此对流换热效果减弱。在上壁面对流换热能力下降时，温度依然有所降低，这主要是因为热流分配发生了明显变化。变化过程主要表现为：下壁面和侧壁面分配的热流显著提升，而总热流是一定的，所以上壁面承受的热载荷降低，导致温度降低。

图11 考虑浮升力时Case B不同横截面的二次流动Fig.11 Secondary flow at different cross-sections for Case B with effect of buoyancy

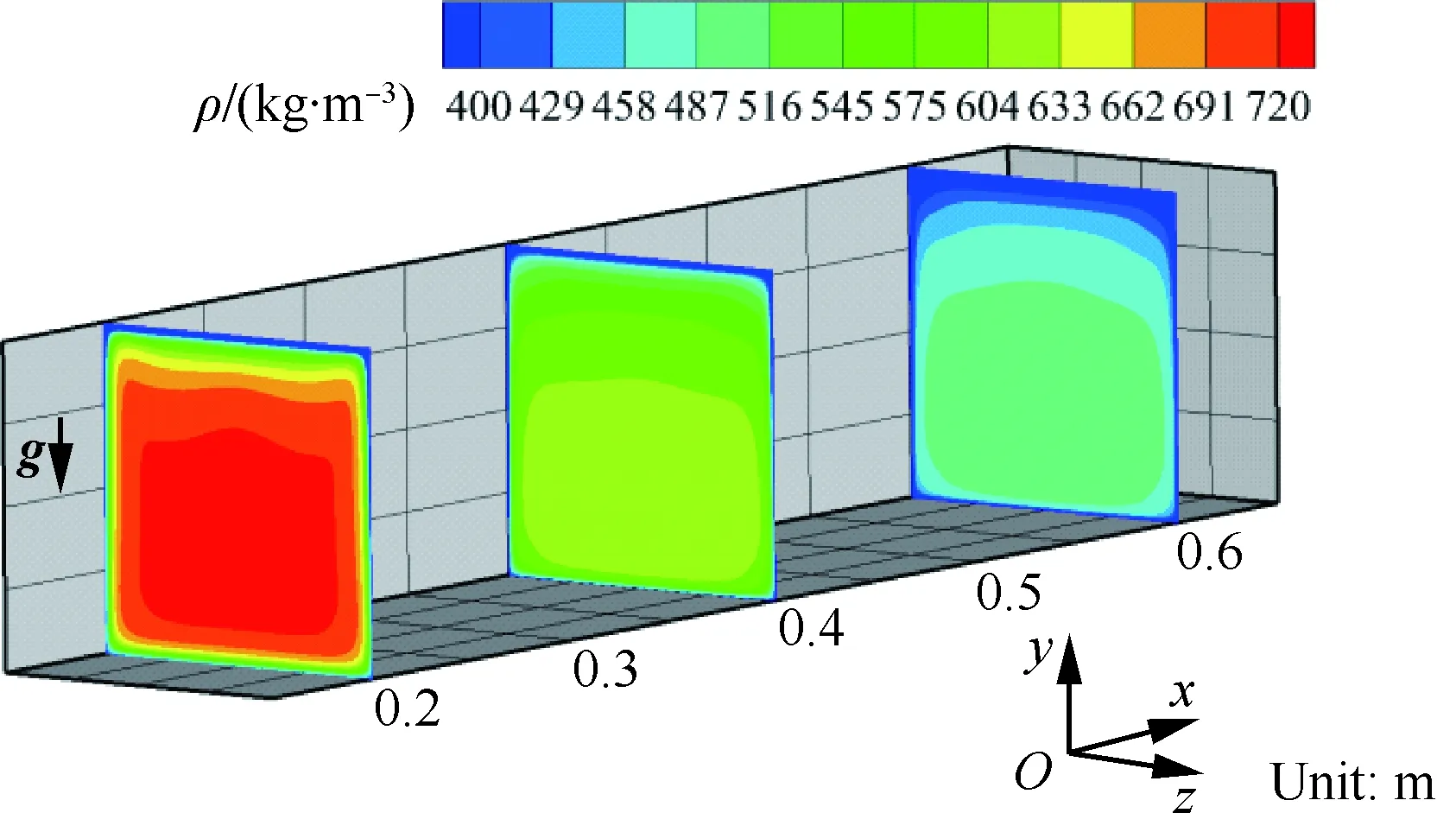
图12 考虑浮升力时Case B不同横截面密度分布Fig.12 Distribution of density at different cross-sections for Case B with effect of buoyancy

图13给出了Case B对流换热系数沿流向的变化情况。考虑浮升力时，上壁面平均对流换热系数降低约7.9%，而侧壁面和下壁面平均对流换热系数分别提升了13.7%和13.6%，传热得到强化。

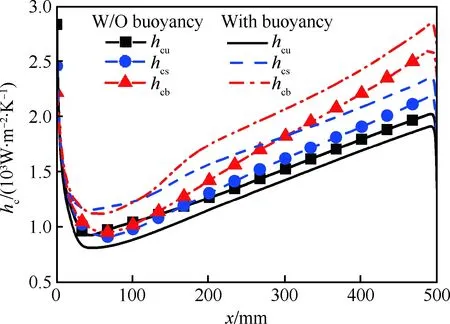
图13 Case B内壁面平均对流换热 系数沿x方向的变化Fig.13 Variations of averaged convective heat transfer coefficients at interior surfaces along x direction for Case B

3.3 燃烧室左侧冷却通道

燃烧室左侧和右侧的冷却通道具有对称性，只需选取其中一侧进行研究。对于燃烧室左侧冷却通道，重力加速度沿+z方向，垂直于热流方向，计算模型并不具有对称性，需要用完整的冷却通道模型。该工况对应的计算模型为Case C。

图14给出了Case C内壁面平均温度沿流向的变化情况。由于计算模型不对称，需要同时考虑冷却通道的两个侧面。本文用下标L和R分别表示冷却通道的左侧和右侧壁面(例如图15中的Tws_L和Tws_R分别表示左侧壁面和右侧壁面的平均温度，对于不考虑浮升力的情况，Tws_L=Tws_R=Tws，其他参数也与之类似)。浮升力使各内壁面的平均温度均有所降低，上壁面温度降低最明显，最多降低约30 K。Case C不同横截面的详细温度分布如图15所示，可以看出虽然高温流体主要集中在冷却通道左侧壁面附近，但左右两侧壁面的平均温度差别很小，如图14所示。这与热流再分配相关，将在后面给出具体解释。

图16为Case C冷却通道各内壁面的平均热流密度变化情况。浮升力使得冷却通道的热流重新分配，进而影响碳氢燃料在冷却通道内的流动传热特性。与不考虑浮升力相比，左侧壁面平均热流密度降低约18.8%，而右侧壁面平均热流密度升高约10.4%。此外，上壁面平均热流密度升高约7.8%。相比之下，下壁面热流密度受浮升力的影响较弱。

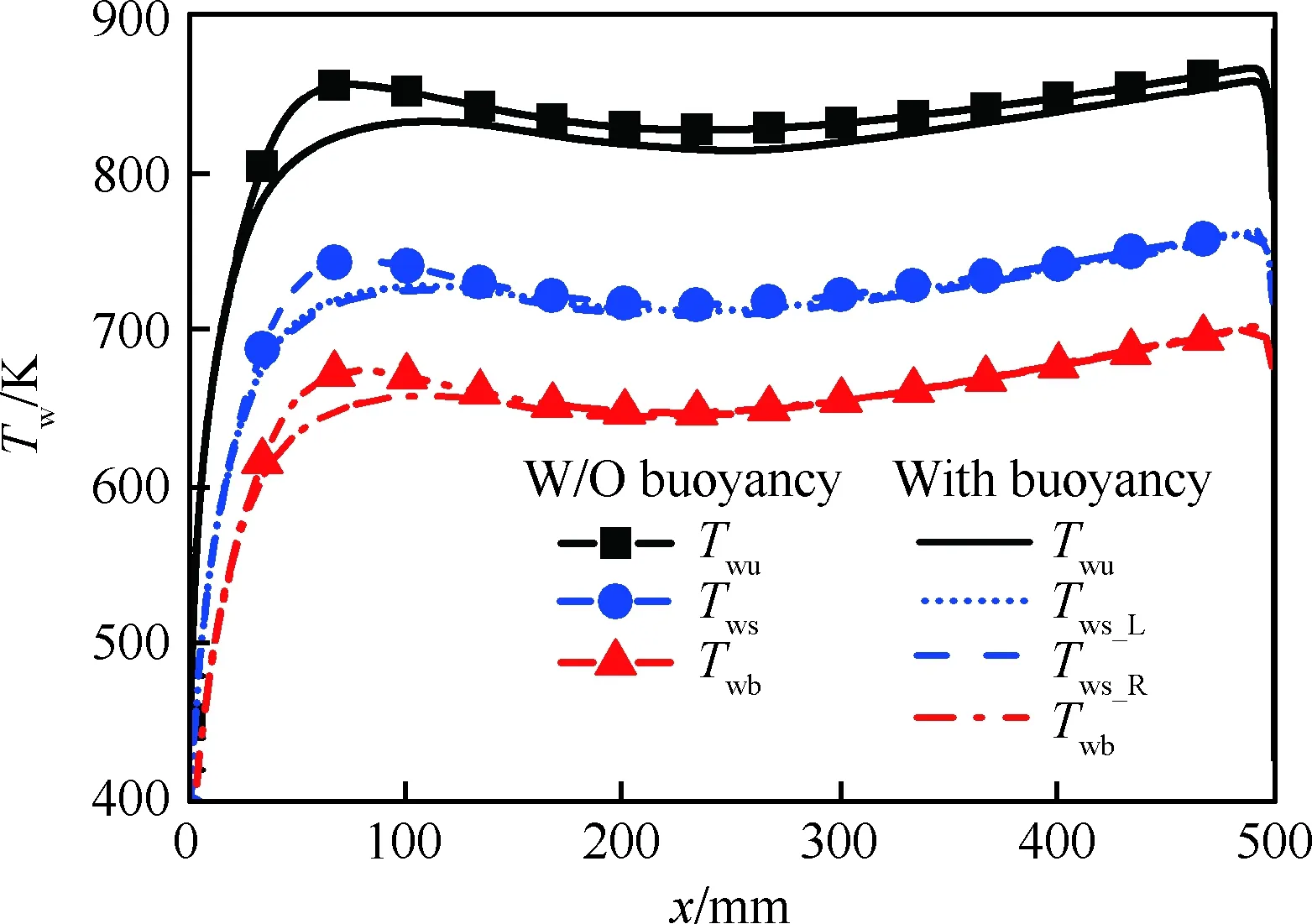
图14 Case C内壁面平均温度沿x方向的变化Fig.14 Variations of averaged interior surface temperature along x direction for Case C

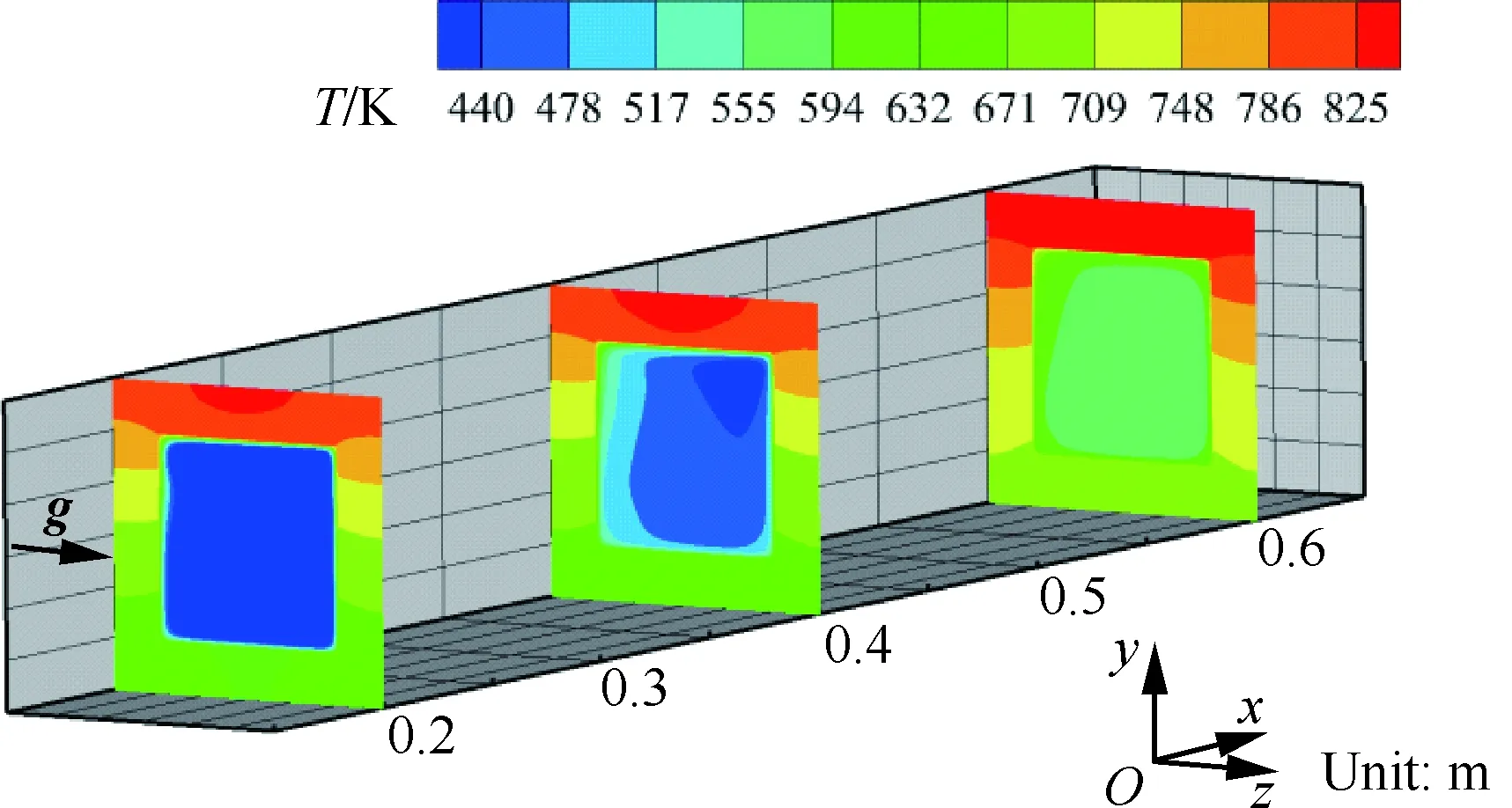
图15 考虑浮升力时Case C固体和 流体区域温度分布Fig.15 Distributions of temperature in solid and fluid regions for Case C with effect of buoyancy

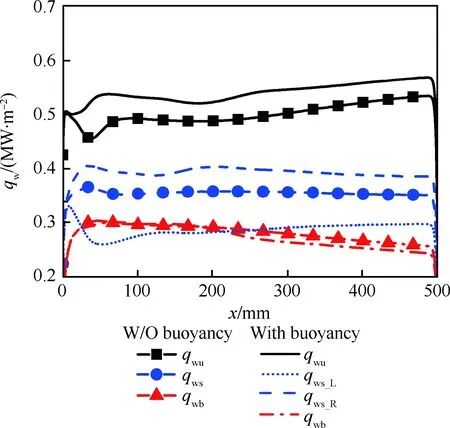
图16 Case C内壁面平均热流密度的变化Fig.16 Variations of averaged interior surface heat fluxes for Case C

图17和图18分别给出了Case C不同横截面的密度分布和二次流动速度分布(图18中uz为z向速度分量)。由图可知，中心区域温度较低的高密度流体向右侧壁面流动，使右侧壁面的对流换热能力增强，温度降低，进一步使右侧壁面分配的热流密度增大。同时，上下壁面附近的高温低密度流体向左侧流动，产生较大的z方向速度分量，出现了二次流动，其中上壁面处的二次流动更加明显。二次流动使上下壁面的流动换热能力增强，温度降低。由于上壁面离加热面更近，换热能力增强后分配的热流明显增大。冷却通道左侧附近汇聚了大量高温低密度流体，导致该处换热能力下降。虽然左侧换热能力下降，但是热流分配时已主要集中在右侧和上侧壁面，左侧壁面承受的热载荷明显降低，因此温度也有所降低。最终冷却通道左右两侧壁面的平均温度差别很小，如图14所示。

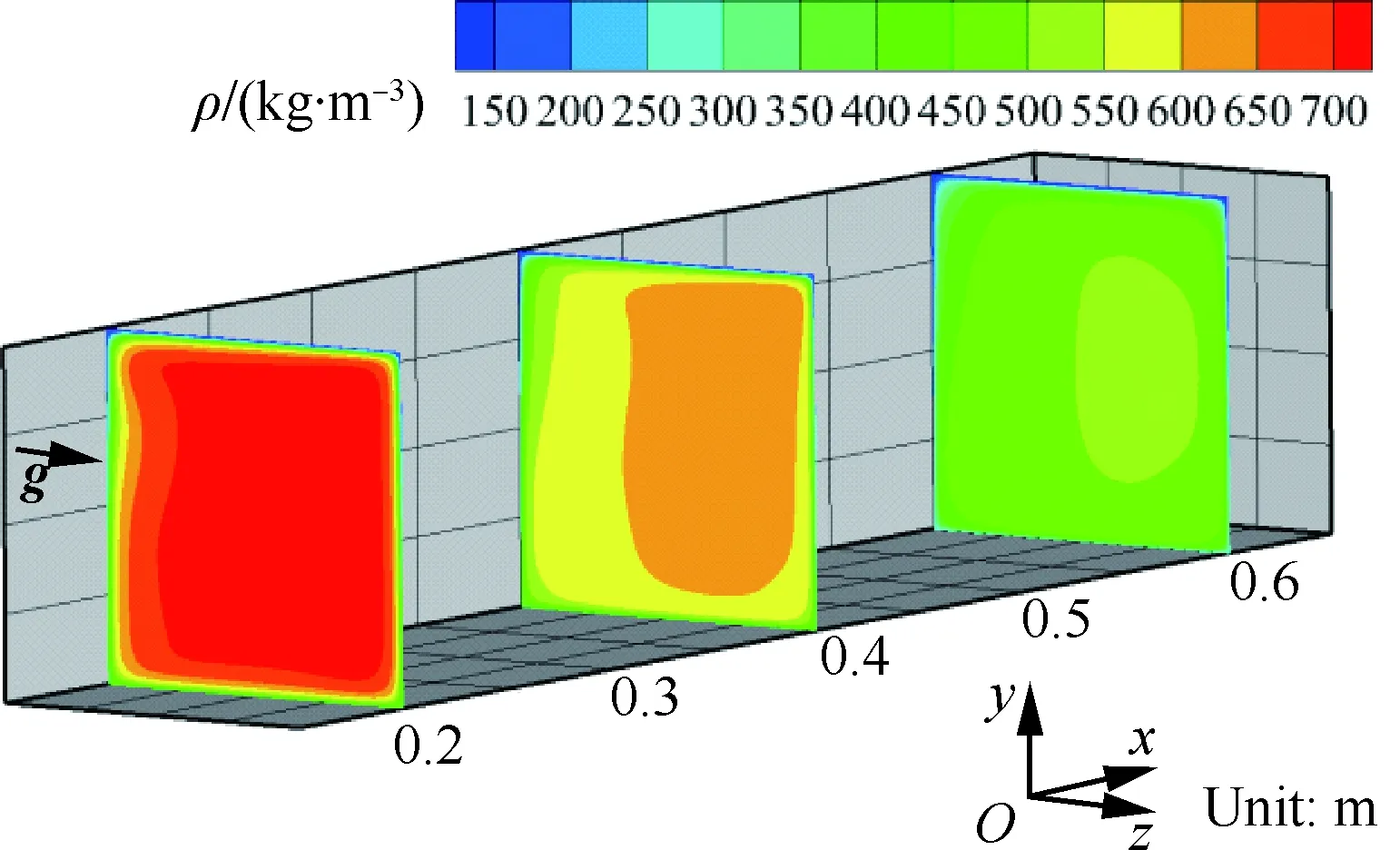
图17 考虑浮升力时Case C不同横截面密度分布Fig.17 Distribution of density at different cross-sections for Case C with effect of buoyancy

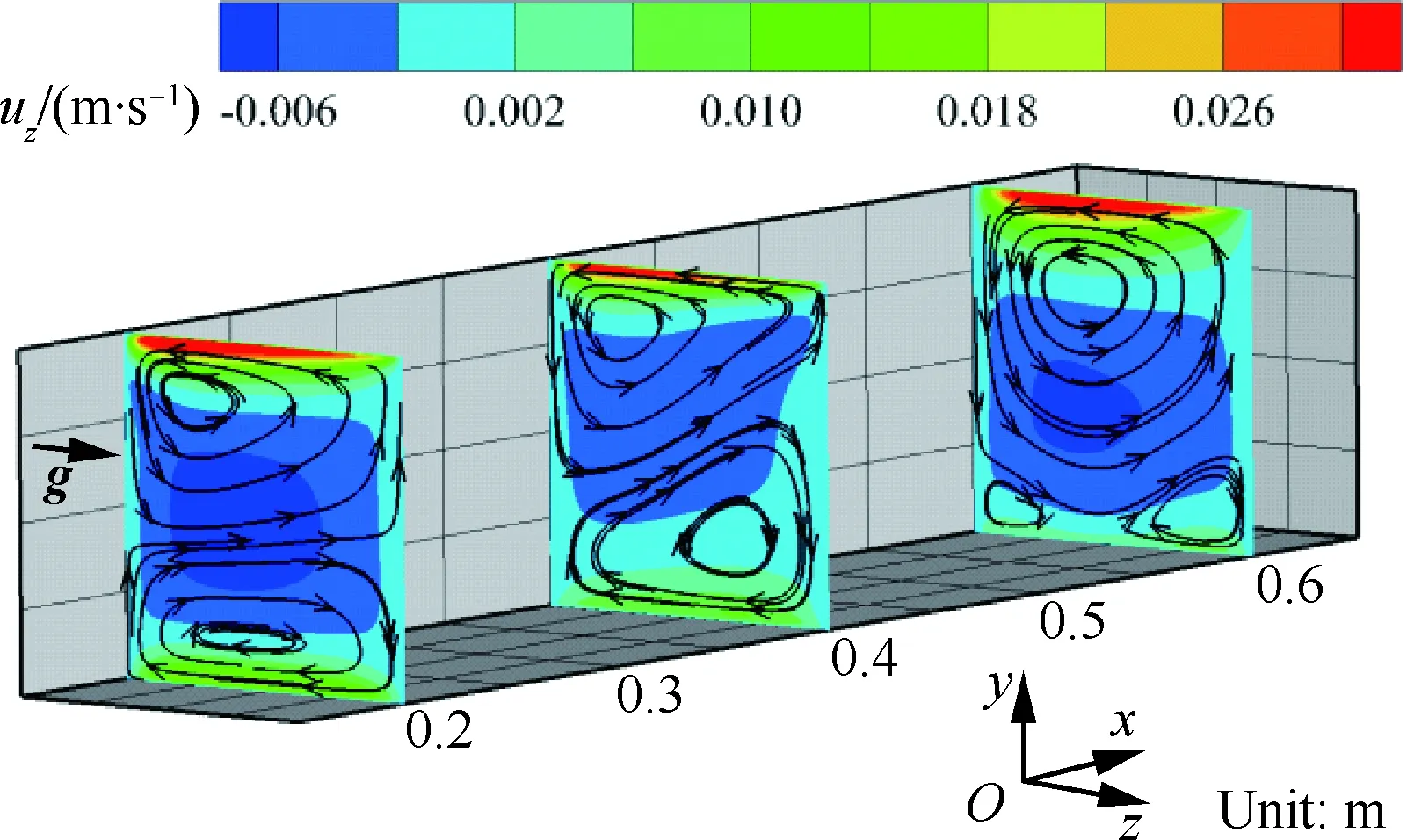
图18 考虑浮升力时Case C不同横截面的二次流动Fig.18 Secondary flow at different cross-sections for Case C with effect of buoyancy

当前工况下，上壁面内侧热流密度明显大于下壁面，因此上壁面对流体的加热能力更强，导致上壁面附近流体密度的降低更加明显，二次流强度增加。高密度流体区域不断向下壁面偏移，在一定程度上抑制了下壁面处的二次流。从图18中也可以看出，沿着流动方向，上壁面始终存在明显的二次流动，而下壁面二次流动强度逐渐减弱。

图19给出了Case C各壁面对流换热系数沿流动方向的变化情况。浮升力作用使冷却通道上壁面对流换热能力显著提升，平均对流换热系数提升了11.2%。此外，考虑浮升力影响时，冷却通道左右两侧对流换热能力变化趋势截然相反，其中左侧壁面对流换热系数下降16.8%，而右侧对流换热系数提升了13.2%。与不考虑浮升力相比，下壁面后半段换热能力出现明显的下降，这与二次流动强度的变化规律是一致的。

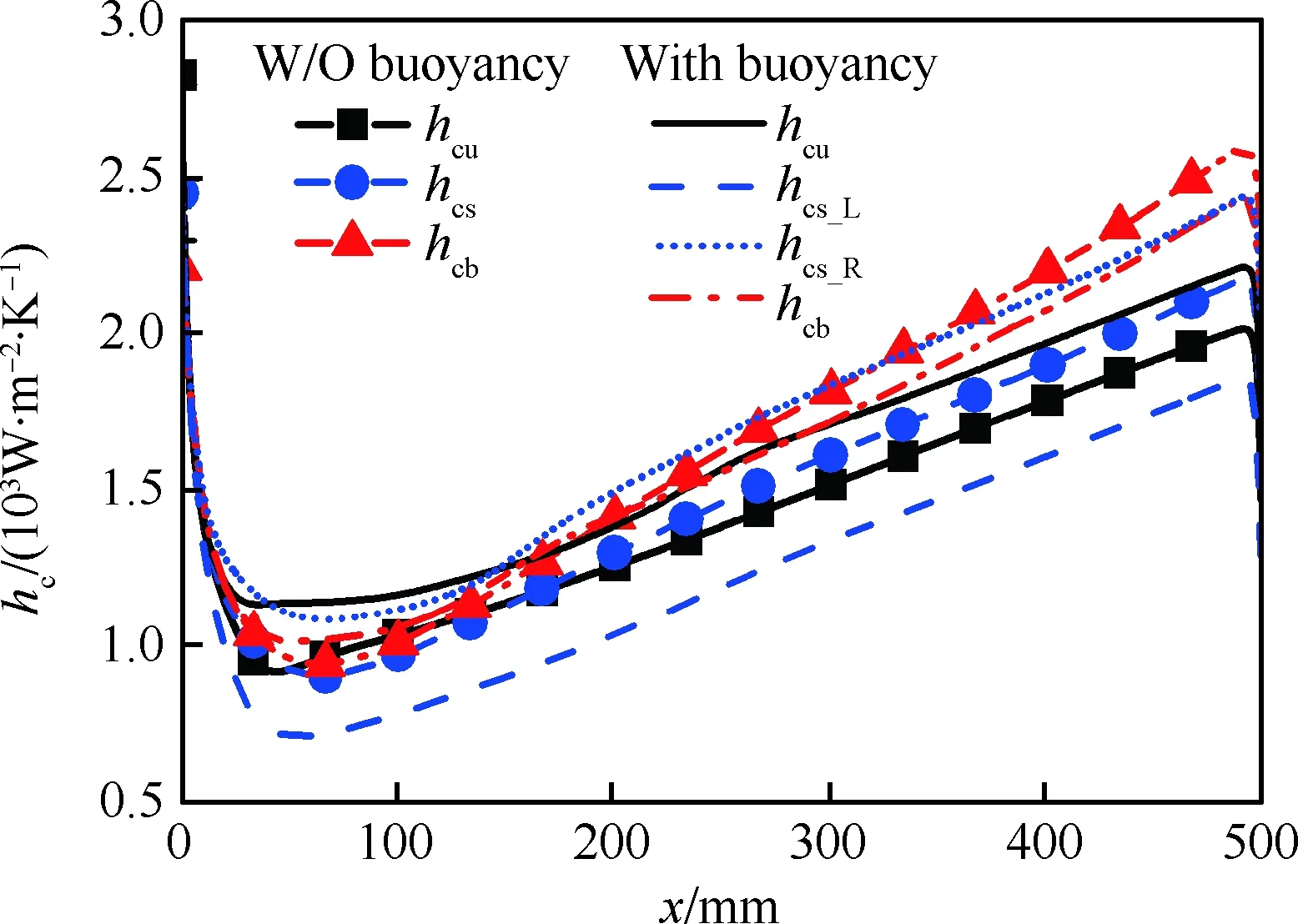
图19 Case C内壁面平均对流换热 系数沿x方向的变化Fig.19 Variations of averaged convective heat transfer coefficients at interior surfaces along x direction for Case C

3.4 换热性能评估

3.1节～3.3节研究了不同位置冷却通道各壁面的热流分配和传热特性，主要用于揭示浮升力的作用机制。在实际工程应用中，冷却通道的整体换热性能需要进一步进行评估。本文采用加热面(上壁面)外侧平均温度来评价浮升力对不同位置冷却通道的强化换热效果。

冷却通道加热面与发动机燃烧室内的高温燃气接触，其表面温度直接反映了冷却通道的冷却效果。加热面外侧平均温度(Tw_uo)变化如图20所示，可以看出，浮升力对Case B的影响程度最为明显，冷却效果提升最为显著。相比之下，浮升力对Case A和Case C加热面的温度影响程度较弱，但换热效果依然有所提升。

图20 加热面外侧平均温度变化Fig.20 Variations of averaged exterior surface temperature at heated wall

4 Nusselt经验公式在考虑浮升力时的适用性

方管沿轴向Nusselt数的计算表达式为

(9)

Jackson & Hall(J & H)经验公式[25]是目前使用较多的换热经验公式，其具体表达式为

(10)

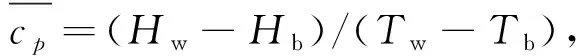
(11)

式中：Tpc为拟临界温度。

由式(10)可知，Jackson & Hall经验公式考虑了物性随壁面温度的变化。由3.1～3.3节可知，浮升力改变了冷却通道的各壁面温度，温度变化必然会引起物性发生变化。因此，本文进一步探讨该经验公式在考虑浮升力时的适用性。

图21为采用Jackson & Hall经验公式与数值计算得到的不同壁面平均Nusselt数沿x方向的变化。由图可知，Jackson & Hall经验公式结果与计算结果的趋势基本一致。不考虑浮升力时，经验公式与计算结果误差在20%以内，满足工程上的计算需要。

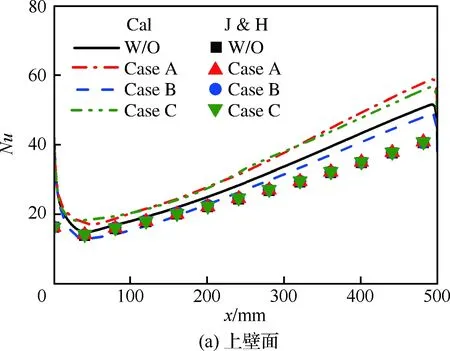
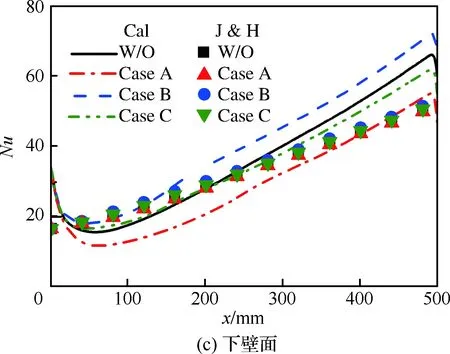
图21 不同壁面平均Nusselt数沿x方向的变化Fig.21 Variations of averaged Nusselt number along x direction under different wall surfaces

由计算结果看，浮升力对Nusselt数的影响不可忽略。然而Jackson & Hall经验公式并不能表征出浮升力对壁面换热的影响，需要寻找其他经验公式或直接进行计算分析解决该问题。

5 结 论

1) 浮升力引起的二次流动导致燃烧室不同位置处冷却通道的温度分布和热流分配出现明显的差异。

2) 浮升力提升了燃烧室不同位置冷却通道的换热效果，其中受热方向和重力作用方向相同的冷却通道换热性能提升最多。

3) 位于燃烧室上侧和左侧的冷却通道，浮升力引起的二次流动使得加热面内侧传热效果强化，温度降低，热流密度增大。

4) 位于燃烧室下侧的冷却通道，浮升力使加热面内侧换热能力下降，但是由于热流分配特性的改变，导致该处热流密度降低，所以温度依然有所降低。

5) 在不考虑浮升力时，修正的Jackson & Hall经验公式具有较高的精度，但该经验公式不能表征出浮升力对冷却通道壁面对流换热的影响，需要寻找其他经验公式或使用CFD手段来解决这一问题。