带自由表面的黏弹性介质正演模拟
王常波,田 坤
(中国石化胜利油田分公司 物探研究院,山东 东营 257022)
近地表地震模拟的首要目标是产生包含准确瑞雷面波的地震记录[1],对自由地表产生的瑞雷面波的模拟已经有很多研究,其中Levander提出的应力镜像法应用最为广泛,大量的模拟结果验证了该方法的准确性。但是所有研究都基于完全弹性介质。对黏弹性介质的研究,1984年Day和Minister首先将实际衰减加入到时域计算[2];1987年Emmerich和Korn采用由n个Maxwell体和一个弹性元件并联组成的广义Maxwell体模型进行了模拟[3];1988年Carcione等研究了由n个标准线性固体并联组成的广义标准线性体模型[4]。在这些模型的基础上,后续发展了很多黏弹性介质的正演模拟研究,但是都没有考虑自由表面的影响[5]。笔者将二者结合,对带自由表面的黏弹性介质进行正演模拟,并对几种典型模型进行计算,重点考查黏弹性介质中瑞雷面波的影响。
1 黏弹波动方程
对于线性黏弹性介质来说,应力应变之间是卷积关系,n维黏弹性介质的张量应力应变关系[6]为
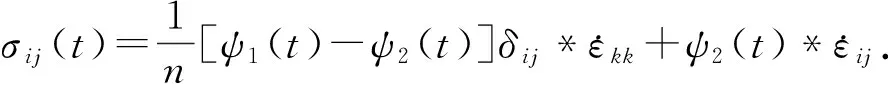
(1)
式中,σ为应力;ε为应变;n为空间维数;t为时间;下标i,j取1,…,n;ψ1(t)和ψ2(t)为松弛函数;δij为单位冲激函数。
对于标准线性体来说,松弛函数和复模量分别表示为
v=1,2.
(2)
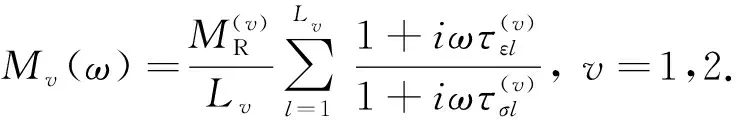
(3)
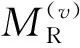
将式(2)和(3)代入式(1),并结合运动平衡微分方程,推导得到黏弹性介质一阶速度-应力波动方程:
∂tρvx=∂xσxx+∂zσxz,
∂tρvz=∂xσxz+∂zσzz,
∂tσxx=(λU+2μU)∂xvx+λU∂zvz+
∂tσzz=λU∂xvx+(λU+2μU)∂zvz+
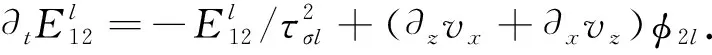
(4)
其中
Θ=∂xvx+∂zvz,
λU=(λR+μR)MU1-μRMU2,
μU=μRMU2,
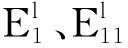
2 自由边界条件
本文中采用交错网格有限差分法求解波动方程(4),采用应力镜像法计算近地表的应力z向导数。
在二维情况下,自由表面条件为
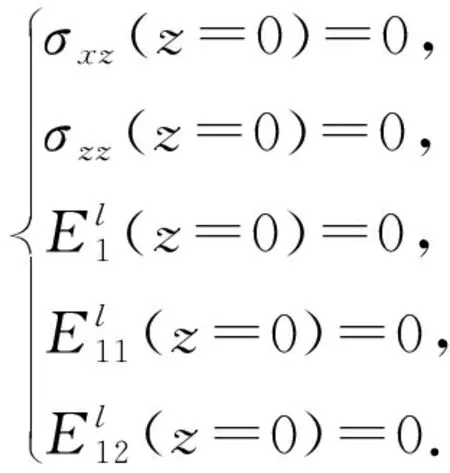
(5)
式(1)与速度自由表面条件等价:
(6)
对于近地表应力波场,采用应力镜像法(以四阶为例):
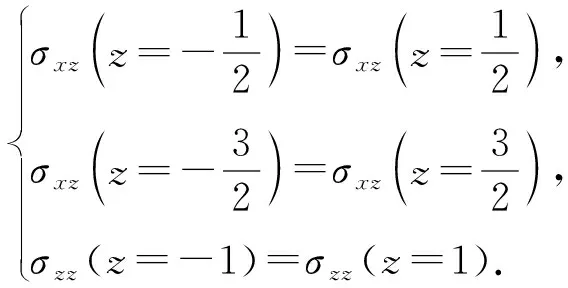
(7)
采用常规交错差分格式可以利用式(7)计算所需的近地表应力z向导数,从而求解方程(4)。
3 模型试算
3.1 均匀半空间介质模型
首先测试均匀半空间模型,分别对弹性模型和衰减程度不同的两个黏弹模型进行正演。图1分别是三个模型的x分量单炮记录,由图中可以看出三个记录都有①纵波和②瑞雷面波两个同相轴,波场在黏弹模型中会产生衰减,Q减小,黏弹性增大,衰减越厉害。瑞雷面波的衰减比纵波剧烈,这是因为瑞雷面波可以看做纵横波的相互干涉,而横波Q比纵波小的多。三个记录中都没有明显的面波频散,说明均匀介质不会发生面波频散现象。
图2是上述三种模型在0.4 s时的x分量波场快照,可以看出,三个波场快照的形态差别不大,各个波型都能够被正确模拟,主要存在①纵波②横波③S*波④瑞雷面波,由于S*波能量随深度减小而减小的缘故,在地表接收的炮记录中不存在S*波。
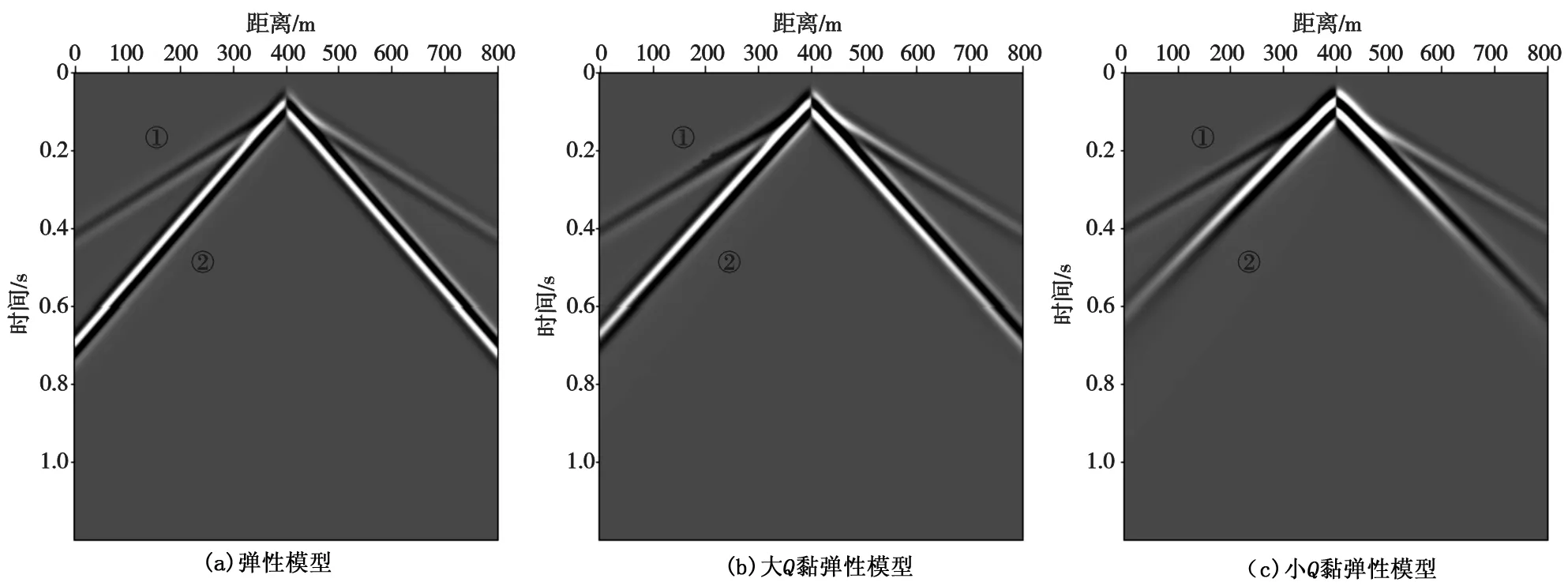
图1 不同均匀半空间介质的x分量单炮记录
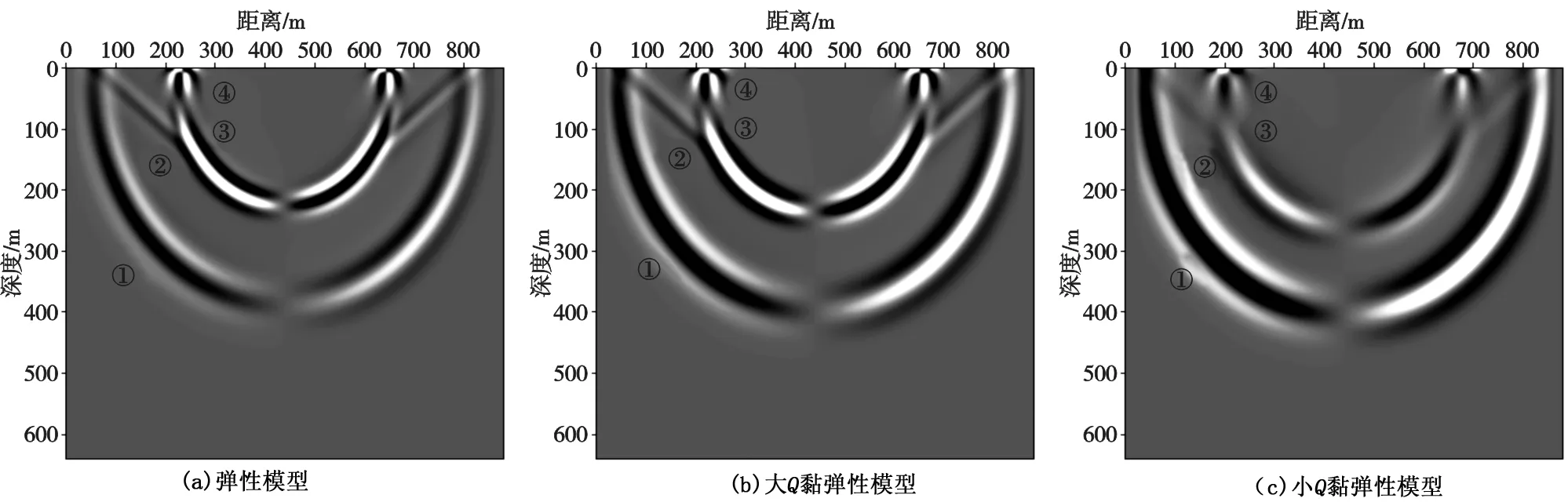
图2 不同模型的波场快照x分量(t=0.4 s)
3.2 三层软弱夹层介质模型
对三层模型进行正演模拟,中间层低速、小Q,同样对弹性、不同程度的黏弹性介质进行计算。图3是三种模型的z分量单炮记录。三种模型中都存在面波频散,而且会受黏弹性严重影响。由于面波频散能量主要集中在中远偏移距,而黏弹介质中存在固有速度频散与振幅衰减,因此黏弹介质的面波能量变弱,同相轴变粗,分辨率降低,细节模糊,使得面波频散不如弹性模型强烈,因此很有必要在面波勘探中考虑黏弹性的影响。

图3 不同三层软弱夹层模型的z分量单炮记录
4 结束语
通过对带自由表面的黏弹性介质进行正演模拟研究,重点考查了黏弹性介质中瑞雷面波的影响。对两种模型进行模拟和对比分析发现,均匀介质观察不到明显的面波频散,三层软弱夹层模型中则会发生面波频散;面波频散会受到黏弹性的影响,很有必要在面波勘探中考虑黏弹性因素。

