Stratonovich型随机微分方程的三阶隐式型随机Runge-Kutta算法

袁 玲，汪 慧，梁 静

（安徽新华学院通识教育部，安徽 合肥 230088）

0 引言

本文研究Stratonovich型标量自治的随机微分方程[1]如下：

其中，W(t)={Wt,t0≤t≤T}为标准维纳过程，f与g是[t0，T]×R上均满足Lipschitz条件与线性增长条件的可测函数。本文运用彩色树理论[2]，构造求解该方程的三阶隐式型Runge-Kutta算法——IMRK算法。

1 三阶隐式型随机Runge-Kutta算法IMRK算法的构造

为了构造3阶隐式型随机Runge-Kutta算法，先选定一个三阶隐式型的确定性Runge-Kutta方法如下将其作为3阶隐式型Runge-Kutta算法的确定性部分，则可以设在隐式型Runge-Kutta算法的Butcher表[3]中有：

则使上述算法具有1.0阶全局收敛性的充要条件[4]是：

不超过1阶的树只有树1、树2和树6；1.5阶的树为树4、树5、树20和树22，它们的Stratonovich型局部误差系数[3]如下：

由此推出的等价方程为：

树4、树5、树20和树22对应的阶条件为：

再以得到最小主误差常数[4]的原则推出相应的等价方程为：

运用已知条件aT和A，并且取，解得满足上述方程组（*）和（**）的一组解为

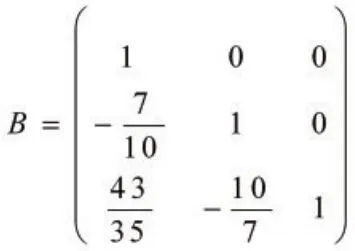
即得到了具有最小主误差常数的强1阶收敛的3级隐式型随机Runge-Kutta算法，并将其称为IMRK算法。

IMRK算法具体如下：

2 IMRK算法的均方稳定性

结论：IMRK2算法的均方稳定函数[5]为R(p,q)，其中

证明：将IMRK2算法（3）应用于求解与Ito型线性检验随机微分方程：dy=aydt+bydw(t)

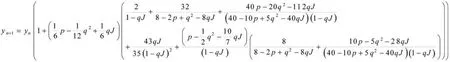
即

则均方稳定函数为：

图1 Runge-Kutta——IMRK算法与5种算法的均方稳定域比较

将隐式型随机Runge-Kutta算法——IMRK算法与 Euler算法[1]，Heun算法[2]，Milstein 算法[4]，PL算法[6]，M2算法[4]的均方稳定域比较如图1。由图像可知，IMRK算法具有更广的稳定区间，即本文构造在稳定性方面具有其自身的优势。

3 IMRK算法精度数值实验

选取方程：

取a=-26，b=1，用平均误差[7]M来表示算法的精度，，其中，和分别表示第次模拟时在点处的数值解和准确解，是模拟次数取为，比较结果如表1所示。

表1 不同步长时误差精度比较

从表1中可以看出，本文的IMRK算法与现有算法相比，具有更高的精度。