供应服从季节性波动的血液供应链优化研究

赵康利，雷雅然

（阿坝师范学院经济与管理学院，四川 汶川 623000）

0 引言

随着生活水平的不断提高，人们对于医疗与健康系统服务有了更高的要求。血液是医疗健康系统中的重要资源，保障血液供给是确保服务质量的关键[1]。血液是一种来源唯一、不可替代、短缺成本极高的特殊易逝品，高库存水平虽然可以保障供应，但会产生极大浪费，从而影响人们的捐献热情[2-3]。因此，保障血液供应，同时减少浪费，是血液供应链优化的首要任务。

由于人体是血液的唯一来源，人的捐献行为具有极高的主观性，因此，血液供应是高度不可靠的。学者们已经关注到这一特点，并对供需双重不确定环境下的血液供应链优化问题展开了研究[4-6]。同时，学者们也关注到供需模型对供应链绩效的影响。在需求的刻画上，大部分研究都以泊松分布描述血液的随机需求[7～10]，也有学者以回归模[11]等方法描绘血液需求。与此同时，学者们也考虑到了需求服从季节性波动的血液供应链优化问题，如文献[12]以某大型医院的血液库存系统为研究对象，建立了系统需求季节性变动的离散事件系统仿真模型。文献[13]构建了捐献者的到达模型，并以季节性的自回归移动平均模型刻画了血液需求。在不确定供应的描述上，文献[14]通过正态分布模型对血液供应进行了描述。然而，血液的季节性短缺已经成为了中国医疗与健康系统的常态[15]，但血液供应呈季节性波动[16]的血液供应链优化问题却尚未被学者研究，也没有学者讨论不同季节性分布模型下的血液供应链优化问题。

由于血小板是保质期最短的血液产品，其最大保质期一般只有5天，因此，血小板供应链管理更加复杂和困难。本文以血小板为例，研究了4种供应波动环境下的血液供应链优化问题，通过数学建模、供应链多周期运营仿真和优化求解，输出血液供应链的系统过期率，以探究供给环境、控制策略对血液供应链的影响。

1 模型假设

本文构建了供需不确定环境下，由1家血液中心和3家医院构成的血液供应链系统，并对该系统进行了为期52周的运营仿真，以遗传算法进行求解，探究供应服从多种季节性分布的血液供应链运营绩效。在血小板的生产和需求方面，我们假定血液中心的实际产能受到季节变动的影响，并表示为（1）[17]。

其中，St代表第t期血液中心的实际供应量，base代表基准产量，slope代表变化率，season代表第t期所处的季节，SeasonalCycle代表季节周期，本文假定SeasonalCycle=7，noise是生产噪音，snormal（）代表正态分布的随机数，具体的特征参数值如表1。

表1 生产函数参数设置

CON生产模型是一种没有趋势性和季节性波动的供应模型，实际产量只受到生产噪音的影响；SEA生产模型则是具有季节性变化的供应模型，它是在CON模型的基础上，考虑生产季节性波动的供应模型；SIT生产模型既有季节变化性，又有随着时间推移，生产能力逐渐增强的特性；SDT生产模型有季节变化性和生产能力递减性。为了尽可能地保障血液供应，反映实际血小板供应链情况，我们假定生产符合SIT模型时，基准产量base为计划产量的一半，符合SDT模型时，基准产量base为计划产量的1.5倍。

在血小板需求方面，假定患者对血小板的需求服从泊松分布[8-10]，同时，患者的需求只能通过医院得到满足，而不能通过血液中心被满足。医院和医院之间不存在血液转运的情况。每一家医院每周每天的需求均值λ如表2所示。

表2 3家医院的平均血液需求mL

同时，本文假定血液中心对血小板的生产及运输耗时为1天，即订货提前期为1天；运输过程中不存在血小板的浪费。

2 数学建模

通过数学模型描述血液供应链运作流程可以更加清楚、准确地描绘血液供应链运作的各个细节，是血液供应链仿真优化的基础[18]。本文探究了由1家血液中心和3家医院构成的血液供应链系统，供应链上的各个成员的补货决策、绩效评价等均可以以数学建模的形式进行表现。血液供应链的日常运作流程如图1所示。

图1 血液供应链运作流程示意图

为了更加清楚地描述血液供应链的运作流程，本文使用数学建模描述血液供应链中的运作流程、评价方式等。数学建模过程中的符号及变量释意如表3所示。

表3 符号释意

首先，供应链上的每个成员每期期末均需要对库存进行更新，库存更新步骤为：（1）满足当天需求后，报废剩余保质期为1天的库存；（2）所有库存的剩余保质期减去1天；（3）加入新收到或生产的血小板。需要注意的是，医院和血液中心在满足患者需求和医院订单时，均采用先进先出（First in First out）的出库策略，该策略可以表示为：

由于供需不平衡，每1期均可能有短缺和过期的发生。第t期，库存水平为时，成员i的短缺数量可以表示为：

其中，x+=max{x,0}。

此时，若有剩余保质期为1天的血小板，则进行报废处理，报废量可表示为：

由此可以将短缺率和过期率表示为：

供应链成员根据更新后的库存状态和最大库存策略进行补货，最大库存策略可以表示为[8]：

血液中心生产血小板后，按照小编号优先级更高的规律制定供货优先级，并采用批量分配方式进行补货。即血液中心优先向优先级最高的医院供货，若有剩余再满足优先级次高的医院。

另外，在供应链控制策略上，考虑了分散控制和集中控制2种策略。其中，分散控制如公式（7）所示，它是指供应链上的每个成员均以最小化自身的过期率为目标的一种控制方式，而集中控制则是优化整个供应链的整体过期率的一种控制方式，可以表示为（8）。

其中Ep表示随机需求分布服从P分布的期望函数，φ是服务水平，本文将服务水平设置为99%，有φ=0.99。

3 仿真优化及结果分析

仿真方法可以更好地揭示血液供应链库存状态的变化和运营风险[7,19-20]，因此，本文运用MATLAB进行仿真，并采用遗传算法进行求解。遗传算法是一种启发式算法，它通过对染色体进行选择、交叉和变异，逐代向最优解靠近，是一种可以获得满意解的全局优化算法。在本文所构建的供应链中，染色体集合为4*364，即：整个运营周期内3家医院和血液中心的最大库存水平。在遗传算法的运算过程中，我们将种群数量设定为50，最大迭代次数为1 000次，淘汰率、交叉率、变异率分别为0.6、0.4、0.1。

由此，通过对所构建的血液供应链进行52周的仿真，并通过遗传算法进行求解，可以得到如表4所示的仿真优化结果。

表4 仿真优化结果

通过表4可以发现，不同的供应波动分布影响供应链的系统过期率。按照系统过期率由低到高可以对供应波动进行简单排序为：SIT，CON，SEA，SDT。这是由于当供应服从SIT分布时，血液中心的初始期生产能力较弱，因此前期总是容易发生供给不足的状态，随着供应能力的增强，血液中心开始有更多库存已满足医院当期需求及上期未被满足的需求，从而使血液中心库存周转率极高，系统过期率低。CON分布则没有季节性波动，血液中心的产量只受到供给噪音的影响，因此供应链的系统过期率较低。而SEA是一种无明显趋势的季节性波动，由于无趋势性，供应链参与者对于血液中心的实际供给没有预期，这使得当供应服从SEA分布时，供应链的系统过期率较高。而当供应服从SDT分布时，供应链系统过期率最高，这是因为SDT是一种呈现下降趋势的季节性波动状态，首先，在研究周期期初，其供应量极高，导致库存积压较多，过期率较高；其次，到研究周期期末，其供应量极低，无法满足市场需求，供应链成员由于对下降趋势的判断和预期，往往会在产量较少的季节下更多的订单，力求供给平衡，但这造成了供应链上更大的波动性，这2个因素使在供应服从SDT分布时，血液供应链系统过期率极高。

另外，研究发现集中控制总是可以实现比分散控制更好的供应链绩效。为了研究不同供应波动分布下，控制策略对于血液供应链的绩效所产生的影响，本文整理了仿真优化结果，并以图2呈现了不同供应波动分布下，控制策略对于血液供应链系统过期率的优化程度。

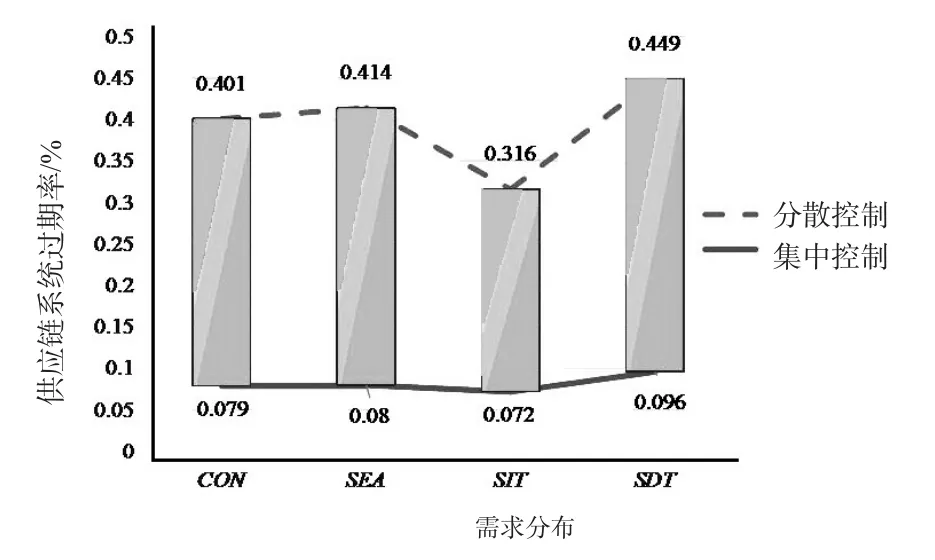
图2 控制策略在不同供应波动分布下的绩效改良程度

由图2可以发现，当供应服从SDT分布时，采用集中控制所带来的系统过期率改良程度最大，而在供应服从SIT分布时，集中控制的改良程度最小。这说明，当血小板供给服从SDT分布时，采用集中控制策略可以极大程度地降低血液供应链的系统过期率；而当血小板供给服从SIT分布时，采用集中控制对血液供应链的系统过期率改良程度较小。这意味着当供应服从SDT分布时，如果对血液供应链采用集中控制需要付出高昂的代价，管理者也依然需要对血液供应链进行集中管理；而当供应服从SIT分布时，管理者可以放弃通过控制策略提高血液供应链管理效率的方法，而采用其他管理办法改善血液供应链的运营绩效。

4 结语

本文以血小板为研究对象，在供需双重不确定环境下构建了由1家血液中心和3家医院构成的血液供应链，并运用MATLAB进行了为期52周的系统仿真，采用遗传算法对问题进行了优化求解。通过仿真优化结果可以发现：（1）在任何供应环境下，采用集中控制都可以极大程度地降低血液供应链的系统过期率，在4种供应状态下，采用分散控制的平均过期率为39.5%，而采用集中控制所实现的系统过期率为8.2%；（2）当供应服从SIT分布时，控制策略对过期率的改善程度相对较小，因此若此时实现集中控制的管理成本极高，则可以采用其他方法控制血液供应链系统过期率；（3）当血液供应服从SDT分布时，集中控制可以更加有效地改善血液供应链的运营表现。

然而，本文没有探究血液供应分布模式和血液供应链中血型替代使用的问题，也没有对医院和医院之间的血液转运、分批运输血液等问题进行进一步的研究，这些都将是作者未来的研究方向。