不定积分运算中的待定系数法再研究

樊庆端,王国强

(上海工程技术大学数理与统计学院, 上海 201620)

1 待定系数法

不定积分的计算是高等数学中非常重要的一部分内容,其方法主要有换元法与分部积分法,还有对被积函数进行恒等变形、化简等方法,这样一些具体问题的求法就会层出不穷[1-2]。待定系数法作为一种重要的数学方法,它在计算有理函数的不定积分与常系数非齐次线性微分方程求解方面已有重要体现,其思想方法是将一个函数表示成另一种含有待定系数的新的形式,令它们相等就得到一个恒等式[3]。根据恒等式的性质得出这些系数应满足的方程或方程组,进而求出待定的系数或其所满足的关系式,这种解决问题的方法叫做待定系数法。该方法在不定积分中应用较多的是有理函数的不定积分,将被积函数表示成至多一个多项式与若干真分式之和,然后通分、运用比较系数法求出系数[4]。简单地说,运用待定系数法的一般步骤:首先确定所求问题所含待定系数的解析式;然后根据题设、数学性质等恒等列出含待定系数的方程或方程组;最后求解得出待定系数或找出待定系数所满足的关系式。本文从待定系数法的角度讨论一些不定积分的计算。

2 不定积分运算的封闭性

函数对求导或不定积分运算的封闭性讨论较少。像指数函数与弦函数(本文中指正弦函数与余弦函数)这样的函数经求导与不定积分运算后函数的类型不变,称它们对求导与不定积分运算都是封闭的。多项式函数不区别次数时,对求导与不定积分运算也是封闭的。以不定积分为例：

对不定积分运算封闭的函数还有很多复杂的类型,比如多项式函数与指数函数之积、多项式函数与弦函数之积等情形,这些不定积分均可用待定系数法进行讨论。

3 运用待定系数法求几类不定积分

3.1 指数函数或弦函数与多项式之积的不定积分

例1 求下列不定积分.

解:(1) 设不定积分的结果为y=e2x(ax3+bx2+cx+d)+C,则

y′=e2x(2ax3+3ax2+2bx2+2bx+2cx+2d+c),

比较系数得 2a=4,3a+2b=0,2b+2c=0,2d+c=5.

解得a=2,b=-3,c=3,d=1.

=e2x(2x3-3x2+3x+1)+C.

(2) 设不定积分的结果为y=(ax3+bx2+cx+d)cos2x+(ex3+fx2+gx+h)sin2x+C,则

y′=(2ex3+3ax2+2fx2+2bx+2gx+c+2h)cos2x+(-2ax3-2bx2+3ex2-2cx+2fx-2d+g)sin2x.

比较cos2x与sin2x系数分别得

联立解得a=c=f=0,b=e=2,

可以看到,两个小题都是求解多元线性方程组来确定系数的,如果采用分部积分法,它们都需要多次分部积分才能完成。

3.2 指数函数、弦函数以及多项式之积的不定积分

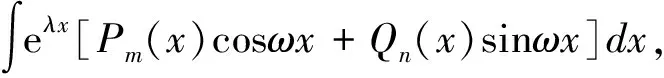
解:设不定积分的结果为y=[(ax2+bx+c)cos2x+(dx2+ex+f)sin2x]e3x+C,则

[(3a+2d)x2+(2a+3b+2e)x+(b+3c+2f)]cos2x+[(3d-2a)x2+(2d+3e-2b)x

+(3+3f-2c)]sin2x=(7x2+9x+4)cos2x+(4x2-5x+7)sin2x,

比较系数可得a=1,b=3,c=-1,d=2,

e=-1,f=2.

所以

3.3 幂函数与对数函数的多项式之积的不定积分

先比较下面三个函数的导数:

[x3(ln3x+ln2x+2lnx+3)]′=3x2(ln3x+ln2x+2lnx+3)+x2(3ln2x+2lnx+2),

[2(ln3x+ln2x+2lnx+3)]′

解:设不定积分的结果为y=x6(aln3x+bln2x+clnx+d)+C,

求导得y′=6x5(aln3x+bln2x+clnx+d)+x5(3aln2x+2blnx+c)

=x5(6aln3x+3aln2x+6bln2x+2blnx+6clnx+c+6d),

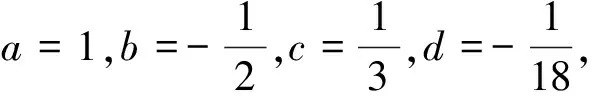
解:设不定积分的结果为y=x(a0+a1lnx+a2ln2x+…+anlnnx)+C,则

y′=a0+a1lnx+a2ln2x+…+anlnnx+x(a1+2a2lnx+…+nanlnn-1x),

这个公式适用于被积函数为幂函数与对数函数之积的情形。如果被积函数是关于对数函数的多项式乘以幂函数,需要展开再利用公式来解。比如前面的例3,运用公式可得解法如下:

4 小结

本文从不定积分运算的封闭性出发,运用待定系数法给出了几类函数的不定积分的计算,避免了大量分部积分法的运用。这些实例表明待定系数法丰富了计算不定积分的方法,在计算量方面也具有一定的优势。除了前面所介绍的,还有幂函数与反正切或反余切函数之积、幂函数与反正弦或反余弦函数之积等几类函数对不定积分运算不具有封闭性,只要明确了不定积分结果中函数的类型,运用待定系数法也可以快捷地计算这些不定积分。