完全保持Jordan零积的映射
张 瑜, 黄 丽, 赵红利
(太原科技大学应用科学学院,太原 030024)
B(H)表示Hilbert空间H上所有有界线性算子的全体.如果A是包含恒等算子的B(H)的C*-子代数且具有前对偶,即存在一个Banach空间使其对偶空间为A,则称A是von Neumann代数。集合Z(A)={S∈A|ST=TS,∀T∈A}叫做A的中心.若Z(A)只包含数量算子,即满足Z(A)=I,则称A是因子von Neumann代数。
von Neumann代数作为性质最好的代数,近些年吸引了越来越多学者的注意.而因子von Neumann代数作为特殊的von Neumann代数,也备受关注。于是,对因子von Neumann代数上相关保持问题的研究也成为了保持问题的发展趋势.2009年,崔建莲、李长京[7]刻画了因子von Neumann 代数上保持斜Lie积的非线性双射.2013年,李长京、陆芳言[1]两位学者证明了因子von Neumann代数上的非线性双射Φ:A→B满足Φ(AB+BA*)=Φ(A)Φ(B)+Φ(B)Φ(A*)当且仅当Φ是*-环同构。特别地,若von Neumann代数是I型因子,则Φ是酉同构或者共轭酉同构。次年,戴丽清[2]等将上述结论推广到了没有中心可交换投影的von Neumann代数上,并证明了满足Φ(AB+ηBA*)=Φ(A)Φ(B)+ηΦ(B)Φ(A)*的非线性双射Φ要么是线性*同构(η不是实数);要么是线性*同构与共轭线性*同构的和(η是实数)。

完全保持问题:定义映射Φn:A⊗Mn(F)→B⊗Mn(F)为Φn((Sij)n×n)=(Φ(Sij))n×n,∀n∈N.若Φn保持Jordan 零积,则称Φ是n-保Jordan 零积的;若对于每个n∈N,Φ都是n-保Jordan 零积的,则称Φ是完全保Jordan 零积的。
完全保持问题对代数结构有很强的约束性,能更确切地反映同态映射的本质.但是,通过查找文献,这方面的结果还比较少(Banach空间的标准算子代数上:完全保幂等性和平方零元、可逆性和谱、谱函数、交换性和Jordan零积、零因子分别参见文献[3-6、10];有限von Neumann代数上:完全保迹秩的映射参见文献[9];无限维复Hilbert空间的*-标准算子代数上:完全保斜Lie零积的映射参见文献[13]),需进一步拓展.鉴于此,本文将在完全保持的框架下讨论Jordan 零积,并证明因子von Neumann代数上这样的满射是线性同构或共轭线性同构的非零常数倍。
1 主要结果及定理证明
定理令H,K是£上无限维Hilbert空间,A,B分别是H和K上的因子von Neumann代数。Φ:A→B是一个满射.则下列叙述等价:
(1)Φ双边完全保Jordan零积;
(2)Φ双边2-保Jordan零积;
(3)Φ是线性同构或共轭线性同构的非零常数倍。
证明满足叙述(3)的映射是双边完全保Jordan零积的,从而(3)⟹(1)⟹(2)是显然的。我们只需证明(2)⟹(3).下面我们假设Φ是双边2-保Jordan零积的。
断言1Φ(0)=0,Φ(I)=cI对某一非零数c成立。
对于∀T∈A,
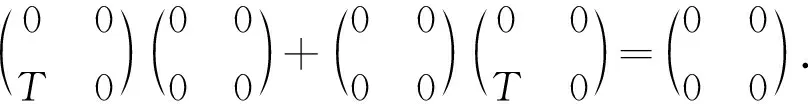
将Φ2应用于上述等式,可以得到


因此,Φ(0)2=0.
(1)
3Φ(0)2+Φ(0)Φ(T)=0.
(2)
由Φ的满射性知,存在某个T0∈A, 使得Φ(T0)=iI. 在(2)式中令T=T0,则3Φ(0)2+iΦ(0)=0. 结 合 (1)式有Φ(0)=0.
下证Φ(I)=cI,对某一非零数c成立。
对于∀T∈A, 一方面

Φ(I)Φ(T)+Φ(I)Φ(-T)=0.
(3)
另一方面
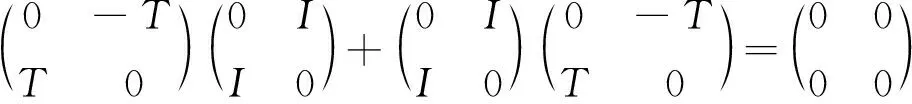
Φ(T)Φ(I)+Φ(I)Φ(-T)=0.
(4)
由(3)和(4)可得:Φ(I)Φ(T)=Φ(T)Φ(I)⟹Φ(I)∈Z(B). 因为B是因子von Neumann代数,所以Φ(I)=cI, 对于任意非零数c都成立。
如果有必要,用c-1Φ来替换Φ. 显然c-1Φ仍然是双边2-保Jordan零积的,故可以假设
Φ(I)=I.
断言2Φ是单射且Φ(-T)=-Φ(T),∀T∈A.
对于∀T,S∈A, 假 设Φ(T)=Φ(S), 则


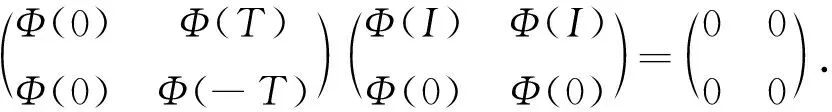
用Φ(S)代替Φ(T), 得
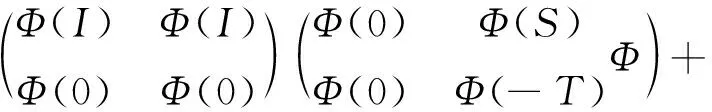

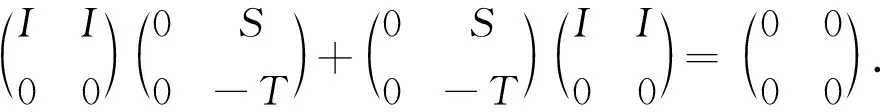
此蕴涵T=S.于 是Φ是单射,从而是A到B上的双射。
由(4)和Φ(I)=I可得Φ(-T)=-Φ(T) ,即Φ(-T)=-Φ(T).
(5)
断言3Φ保可加性,即Φ(T+S)=Φ(T)+Φ(S).
对于∀T,S∈A,
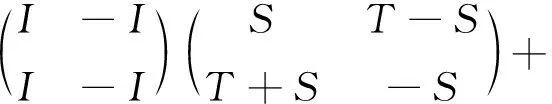
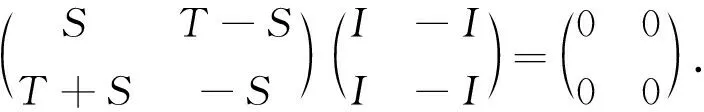
将Φ2应用于上述等式,结 合 (5)式可得Φ(T+S)+Φ(S-T)=2Φ(S).
(6)
又
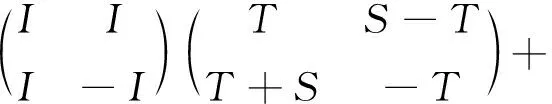

将Φ2应用于上述等式,结 合 (5)式可得Φ(T+S)+Φ(T-S)=2Φ(T).
(7)
由(5)、(6)、(7)联立得到Φ(T+S)=Φ(T)+Φ(S).
断言4Φ保可乘性,即Φ(TS)=Φ(T)Φ(S).
对于∀T,S∈A,

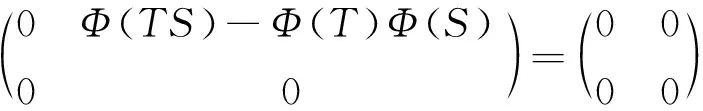
Φ(TS)=Φ(T)Φ(S).
断言5Φ(iI)∈Z(B).
对于∀T∈A,
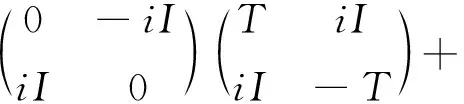

将Φ2应用于上述等式,从而有Φ(iI)Φ(T)=Φ(T)Φ(iI)⟹Φ(iI)∈Z(B).
断言6Φ具有线性或共轭线性。
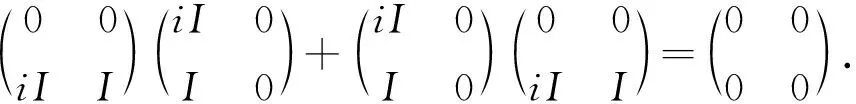
将Φ2应用于上述等式,从而有Φ(iI)2=-I. 根据断言5知Φ(iI)∈Z(B),因此可令Φ(iI)=μI.则(μI)2=-I⟹μ=±i.于是,Φ(iI)=iI或Φ(iI)=-iI.
若α是实数,则Φ(αI)=αI.那么Φ(αA)=Φ(αI·A)=Φ(αI)·Φ(A)=αΦ(A).
若α是复数,令α=a+bi,则Φ(αI)=Φ((a+bi)·I)=Φ(aI)+Φ(b·iI).
根据断言6得到Φ(b·iI)=bΦ(iI)=bI或Φ(b·iI)=bΦ(iI)=-bI.
因此Φ(αI)=Φ(aI)+Φ(b·iI)=aI+b·iI=(a+bi)I=αI
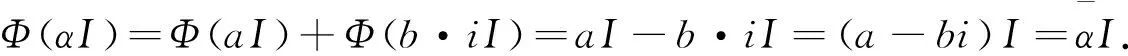

——以指数、对数函数同构问题为例

