基于自适应卡尔曼滤波器的锂电池SOC估计策略

李 华，于少娟

(太原科技大学 电子信息工程学院，太原 030024)

为减少化石能源的消耗和温室气体的排放，电动汽车(EV，electric vehicle)越来越受人们的关注，并将成为交通能源转型的新方向。目前，锂电池各方面性能不理想很大程度上制约着EV的快速发展，因此，有必要对电池的能量管理系统进行深入研究。电池管理系统(BMS，battery management system)被称为电池的“安全管家”，可以优化控制动力电池，保证其优良性能，延长使用寿命[1]。作为BMS的一项核心技术，荷电状态(SOC，state of charge)表征电池的剩余电荷，可以为电池的均衡管理、热管理、安全保护提供数据依据，提高电池的安全性和使用效率。SOC精度是影响EV性能的重要因素之一，因此开发一种精确可靠的SOC算法，对电池乃至整车的能量管理都有重要意义[2]。

锂电池内部化学反应机理复杂，SOC值大多是根据电池的外部特性间接获得。目前主要有库伦计数法，也称作安时积分法(AH，ampere hour integral method)，还有开路电压法、神经网络法、数学模型法、卡尔曼滤波法等[3]。AH法可以用于各种类型的电池，是目前使用较多的方法。电流积分依赖于电流测量精度，测量误差和噪声会使误差不断积累，严重影响SOC的精度，所以这种方法通常用于实验室离线计算[4]。开路电压法(OCV，open circuit voltage)估计SOC需要对电池静置一段时间，使电池内部电荷基本达到平衡，所以该法不能满足电动汽车在线实时估计的要求[5]。神经网络法需要大量实验数据进行训练，运算量较大，且估算精度依赖于训练方法和训练数据。数学模型法受电池使用环境影响较大，当使用工况变化时，需要不断对SOC进行校正。卡尔曼滤波法通过反复迭代运算可以有效地解决SOC初值问题，降低累积误差的影响，但是这种方法对电池模型的精确性要求较高，并且当系统误差协方差和观测误差协方差所设置的常值不合适时，卡尔曼滤波器的精确性也会受到严重的影响，甚至会造成SOC估计结果的发散[6]。

针对以上方法对SOC估计精度不高且实用效果不理想等问题，本文在文献[10]的基础上，基于改进的RC等效电路模型，采用了自适应扩展卡尔曼滤波器(AEKF，adaptive extend kalman filter)，即在EKF原理的基础上引入自适应协方差匹配算法。AEKF有效解决了噪声可变的问题，通过不断迭代更新系统误差协方差和测量噪声协方差系数，增强算法对复杂工况环境的适应能力，使改进的EKF算法对SOC的估计更加精确和稳定，并且可以实现SOC初值的快速校正。

1 电池模型的建立和参数辨识

锂电池本身复杂的动静态特性给SOC估算带来困难，并且卡尔曼滤波器是基于模型的算法，因此我们需要对锂电池建立合适的等效模型。

1.1 SOC状态方程

SOC表示电池可用容量与标称容量的比值，理论上可通过安时积分法获得，如式(1)：

(1)

其中，SOC(t)表示电池在t时刻的瞬时SOC值；η是库伦效率(通常在放电条件下，取η=1)；SOC(0)表示电池在t=0时刻SOC的初始值；i(τ)表示电池的工作电流；QN=1/3600CN，CN表示电池的标称安时容量。SOC状态方程通过对电流的积分值得到一个剩余容量占电池总容量的百分比，再与SOC初值做差即可得到电池各时刻的SOC值。

1.2 二阶RC等效电池模型

电池管理系统开发过程中，通常建立电池的等效电路模型[7]。其中，戴维南等效电路模型的应用最为广泛，但由于模型参数会随着电池运行状态的改变而变化，因此有必要进一步增加模型的精度。本文考虑电池的极化特性，在戴维南等效电路模型的基础上增加一个RC支路，则二阶RC等效电池模型如图1.

图1 二阶RC等效电路模型
Fig.1 Second-order RC equivalent circuit model

图1中，R0是电池的欧姆内阻；R1，R2,C1，C2分别表示与电池暂态响应相关的极化电阻和极化电容；v1表示并联R1C1支路的端电压，v2表示并联R2C2支路的端电压；Eoc表示电池的电动势，也可以表示为OCV，即电池的开路电压，电池Eoc与SOC之间的关系表示如下：

Eoc(t)=f(SOC(t))

(2)

二者的函数关系可以根据实验室测得的电池充放电数据进行标定。

根据图1所示二阶RC等效电路模型可以得出：

v0=Eoc-v1-v2-iR0

(3)

(4)

由式(1)-(4)，选择电容C1、C2上的电压降落v1，v2和SOC作为状态变量，可以得出电池的状态空间模型：

(5)

v0=Eoc-v1-v2-iR0

(6)

式中，状态变量为：

控制变量为u(t)=i；输出变量为y(t)=v0.

由于Eoc与SOC具有高阶非线性关系，所以使得输出方程(6)是非线性方程。将式(5)进行离散化可得：

其中，Δt表示采样周期。

1.3 电池模型参数的辨识

基于以上二阶RC电池模型，通过实验室电池充放电实测数据对电池模型的参数进行辨识。

1.3.1 OCV与SOC的标定

OCV-SOC是一条很重要的曲线，在以上等效电路模型的电压输出方程中，由式(2)可以根据瞬时SOC(t)确定开路电压OCV(即Eoc)，从而计算出电池端电压的预测值v0.另外，电动汽车运行一段时间后，在车辆静置再启动前，BMS也会调用该曲线，对SOC值进行一次校正，并通过一定的算法和其他校正系数得到一个SOC初值的更新[8]。因此，OCV-SOC曲线的准确性非常重要，可能直接关系到SOC的估计精度。

通常采用对电池进行充放电测试的方法来确定OCV与SOC二者之间的关系。本文采用的是A123公司的26650型号磷酸铁锂电池模块，标称容量为23 Ah，额定电压3.3 V，充电截止电压3.8 V，最小放电截止电压2 V.本文通过电池充放电静置实验法来确定锂离子电池OCV-SOC曲线的函数关系。首先进行充电测试，从SOC为0开始以C/2的充电倍率充电5 min，然后静置45 min,使电池内部化学反应几乎达到稳定状态，测量电池开路电压，重复以上过程，直到SOC达到100%.放电测试是从SOC为100%开始，然后以1C放电倍率放电5 min，然后静置45 min之后，测量电池开路电压，重复以上过程，直到SOC为0.锂电池在充放电过程中存在滞回特性，即同一SOC点在充电和放电过程中所测得的开路电压有所差异，但本文忽略其影响，取二者的平均值。经Matlab滤波处理后OCV与SOC的关系曲线如图2所示。

图2 OCV-SOC关系曲线
Fig.2 OCV-SOC relationship curve

基于非线性最小二乘原理，在Matlab中调用lsqcurvefit函数，对实验数据进行非线性拟合，得OCV-SOC的多项式函数关系，如式(7)：

Eoc=a2SOC2+a1SOC+a0

(7)

其中，a0=3.0627，a1=0.0202，a2=-0.005.

1.3.2 RC模型参数辨识

RC并联支路反映电池暂态响应特性，通常采用脉冲放电测试法，利用所测电压电流数据对电池等效电路模型的RC参数进行辨识。实验脉冲电流i(t)测试工况与电池端电压v(t)的采集数据如图3、图4.电池在每一个周期进行一次脉冲放电，持续10 s，脉冲放电电流达到27 A，然后静止2 min，以保证电池在下一个周期到来时电池内部电荷基本达到平衡。通过这种方法，可以很好地获取电池的动态和稳态性能，实现电池参数的精确辨识。

图3 脉冲放电电流
Fig.3 Pulse discharge current profile

图4 电池端电压
Fig.4 Battery terminal voltage profile

在Matlab环境下，利用最小二乘法对电池模型参数进行辨识，使电池模型的输出电压匹配实验室实测的电压值。

二阶RC模型的参数辨识结果如表1所示：

表1 二阶RC锂电池模型参数
Tab.1 Second order RC Lithium battery parameters

R0(Ω)R1(Ω)R2(Ω)C1(F)C2(F)0.02150.07360.0931681458279

为验证电池模型的有效性，通常需要设置一电池测试工况。本文选用图3所示已经测试好的工况，对以上所建立的等效电路模型进行有效性验证。

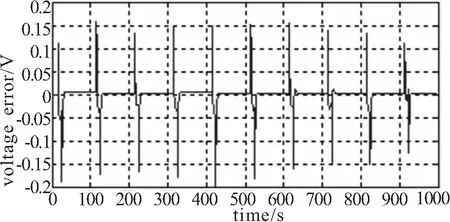
图5 模型输出电压与参考电压的误差
Fig.5 Voltage error between model output voltage and reference voltage

采集仿真模型的输出电压，并与图4所示的电池实测电压参考值进行对比，通过图5所示的电压误差曲线可得，模型的输出误差在0.2 V范围之内，满足实际要求，即表明上文建立的二阶RC电池模型可以很好地反映真实电池的动静态特性。

2 自适应EKF的SOC估计

2.1 基于EKF的SOC估计

卡尔曼滤波器(KF，kalman filter)是一种基于最优滤波原理反复迭代更新系统状态变量的技术，是一种是递归估计器，即利用前一时间步长的预测状态和当前传感器测量值来计算该时刻状态的最优估计，被广泛应用于目标跟踪、全球定位、空间导航、军事等技术领域[9]。扩展卡尔曼滤波(EKF，extend kalman filter)是KF在非线性系统中的应用，基于离散化的线性动态系统，在每一个采样区间，通过一阶泰勒级数将非线性模型进行线性化近似，此过程虽然舍弃了高阶项，但实践证明EKF可以达到很好的估计效果[10]。将EKF技术应用到对锂电池SOC的预测当中，可以有效抑制测量误差和噪声，减轻对SOC初值的依赖。

将式(5)、(6)中电池等效电路模型的状态空间方程写成一般形式：

xk+1=f(xk,uk)+wk

(8)

yk=g(xk,uk)+vk

(9)

其中wk与vk是相互独立，且满足正态概率分布的白噪声，即

(10)

式中，Qk,Rk分别表示系统噪声协方差矩阵和测量误差协方差矩阵。设f(xk,uk)，g(xk,uk)在所有运行点处都是可微的，通过泰勒级数将其进行线性化处理，

(11)

(12)

将式(11)、(12)代入到式(8)、(9)中，即得到描述非线性系统的线性化方程：

(13)

EKF通过一系列反馈控制实现状态的最优估计，具体可以分成两个过程：时间更新和量测更新。时间更新用于预测当前状态及其误差协方差，以获得最优估计状态的先验估计；量测更新用于反馈校正，基于测量值获得一个改进的后验估计，实现传感器测量值与模型输出值之间的最佳折中，从而获得最好的状态估计[11]。

定义状态向量矩阵:

(14)

(15)

在k=0时刻进行初始化：

(16)

(17)

以上循环迭代计算步骤分为五步：

(1)状态估计时间更新:

(18)

(2)状态估计误差协方差时间更新：

(19)

(3)卡尔曼滤波增益更新：

(20)

(4)状态估计的量测更新:

(21)

(5)误差协方差量测更新：

2.2 自适应协方差匹配算法

在进行EKF迭代计算时，测量误差和系统噪声的协方差很难获得，通常预先设定为一个常数，但实际应用当中一般均为时变的动态系统，EKF的估计精度会受到较大影响，恶劣的工况条件甚至会导致滤波器的不收敛[12]。因此，为了改进滤波效果，本文将自适应协方差匹配算法与EKF结合，算法通过对系统噪声协方差和测量误差协方差的实时更新，可以有效解决Qk，Rk参数设置不合理所造成的SOC偏差。

引入自适应协方差匹配算法(AEKF，adaptive extend kalman filter)的主要目的就是为系统提供最新的测量误差协方差和系统噪声协方差，从而有效地计算更新当前的EKF滤波增益，实现系统的快速收敛以及状态变量的最优预测，使SOC预测值更加精确。

(23)

(24)

(25)

其中，Hk是基于开窗估计原理得到的ek的协方差函数；M表示开窗的大小，即累计新息的数量，为避免计算量太大，本文取前三次的差值进行计算，即M=3；Lk为增益矩阵。基于AEKF算法实现SOC估计的流程图如6所示。

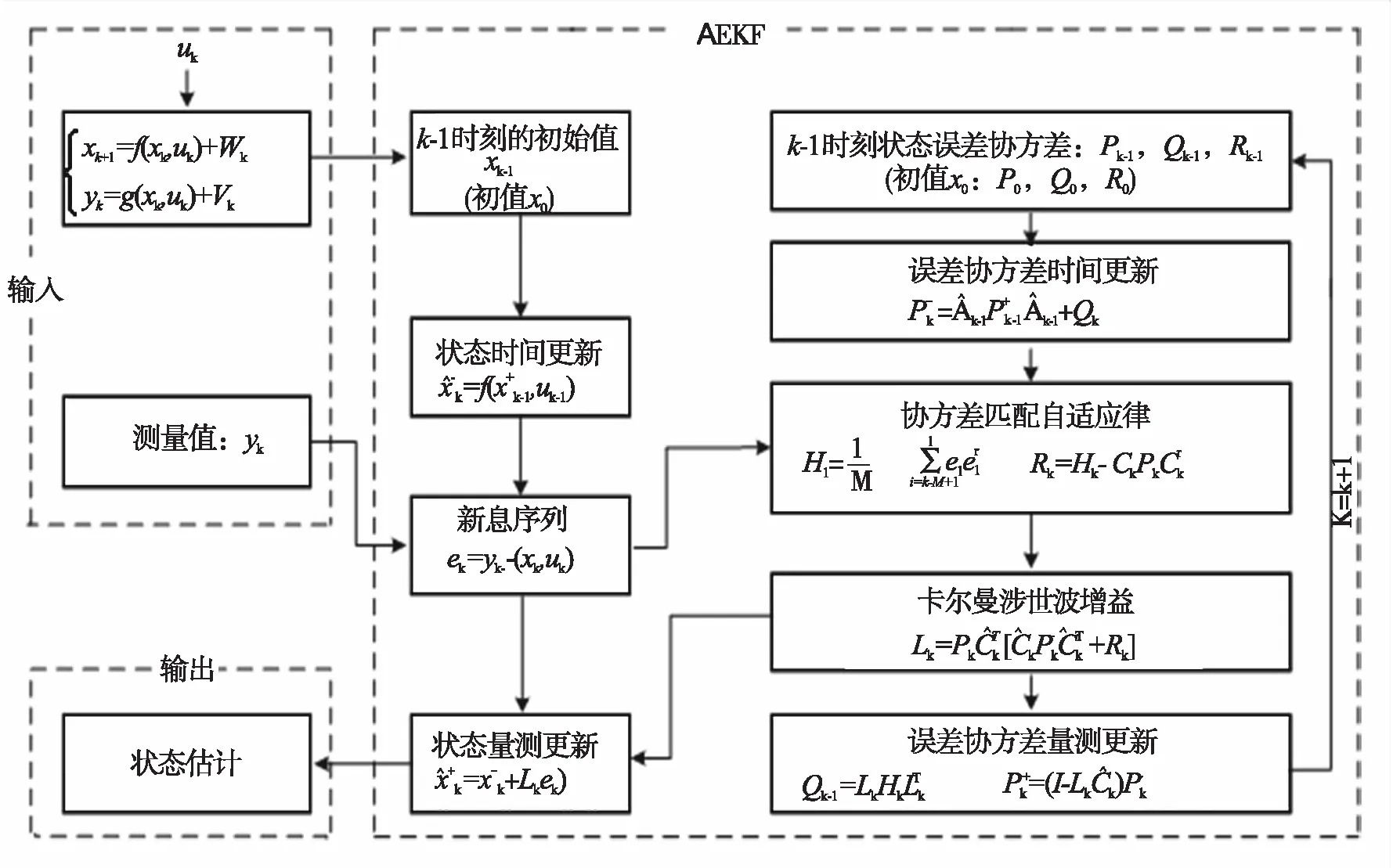
图6 AEKF算法的实现
Fig.6 Implementation flowchart of the AEKF algorithm

以上AEKF算法对电池SOC的预测过程可以简述为：利用库伦计数法递推SOC值，然后代入到电池模型的观测方程中，预测电池的输出电压，同时计算EKF的增益Lk,它反映了残差ek作用于状态变量SOC的权重，最后由状态估计观测更新方程得到SOC的最优估计。这种方法克服了安时积分法的累积误差，同时在算法中考虑了噪声和误差的影响，改进了EKF算法对不确定扰动的适应能力，实现了对SOC状态的闭环估计。

3 仿真实验分析

实验目标电池采用的是A123公司的26650型号磷酸铁锂电池模块，技术参数同第一节所述。在Matlab/simulink环境下建立AEKF 算法的仿真模型，以两段恒流放电实验数据和Advisor下UDDS测试工况的充放电数据作为输入，对所提算法进行相应的仿真分析，并分别与应用AH法和EKF法的仿真结果进行了对比分析。其中，测量误差协方差的初值R0设定为1000，系统噪声协方差Q的初值设定：

(26)

状态估计误差协方差P的初值设定：

(27)

3.1 两段式恒定电流测试工况

电池的恒流工况特性关系电池的倍率特性和温度特性，是研究电池非常重要的特性之一。因此，为验证AEKF算法是否可行有效，首先要在恒流工况下对电池的SOC进行估计。图7表示实验室电池放电电流测试工况，0-1800 s期间进行24 A恒流放电，1800-2700 s期间进行48 A恒流放电。将实时采集的电压电流实验数据导入到Matlab中，然后分别应用AH法和AEKF算法对SOC进行估计，仿真结果如图8所示。

图7 两段恒流放电电流工况
Fig.7 Two-stage constant discharge current profile

由图8所示仿真结果可得，AH法的SOC估计曲线逐渐偏离参考值，估计误差误逐渐增大，如图9所示。说明AH法的估算过程存在累计误差，若不进行校正，随着时间得推移，SOC的估计效果会越来越差。另外，为验证AEKF算法对SOC参考值的快速跟踪性能，在仿真时将SOC初值设为70%(实际电池为完全充满电的状态，即SOC初值的参考值为100%)，从图8可以看出，AEKF算法大约在200s内就可以完成对SOC初值的校正，并且在之后的仿真过程中可以对SOC参考值准确地跟踪，克服了AH法由于累计误差所产生的影响。AEKF估计误差如图10所示，平均误差小于2.4%，满足实际应用要求，说明该算法具有可行性。

图8 AH和AEKF算法的SOC估计曲线
Fig.8 Battery SOC estimation comparison based on AH and AEKF

图9 AH算法的SOC估计误差曲线
Fig.9 SOC estimation error curves with AH

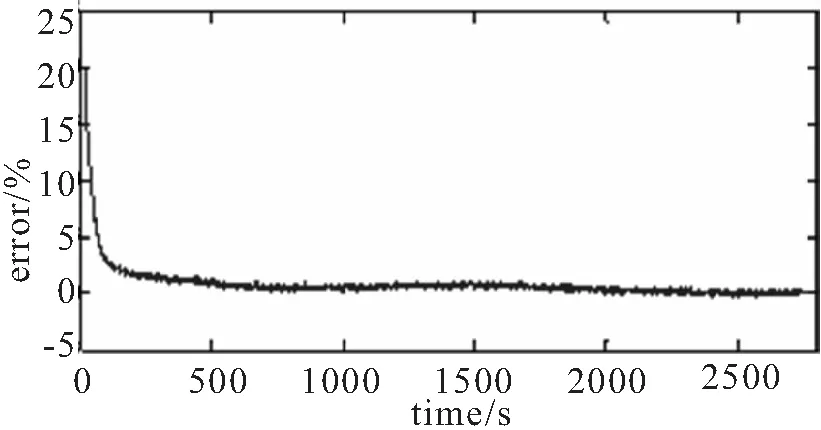
图10 AEKF算法的SOC估计误差曲线
Fig.10 SOC estimation error curves with AEKF

3.2 UDDS测试工况

为验证复杂电流波动条件下AEKF算法对SOC的估计效果，本文采用高级汽车仿真器Advisor(Advanced Vehicle Simulator)提供的UDDS工况对AEKF算法进行仿真验证。UDDS工况是一种可以模拟城市道路中电动汽车频繁启停的城市循环工况，广泛用于汽车整车性能测试，控制策略评估等，是一种很重要的测试工况。

图11表示UDDS的车速工况，EV在测试过程中总停车17次，共行驶1369 s,行驶距离7.45 km,最大车速56.7 km/h,最低车速19.58 km/h,最大加速度4.84 m/s2，怠速时间259 s.图12表示UDDS循环工况下对应的电流工况，反映了锂电池在不同速度工况下电流的变化情况。随着汽车的频繁启停，电流值变化频繁且变化幅度很大，加速过程中产生的最大放电电流可达110 A，EV在制动过程中，最大再生充电电流可达23.9 A.

图11 UDDS工况下的速度曲线
Fig.11 Speed curve based on UDDS drive cycle test

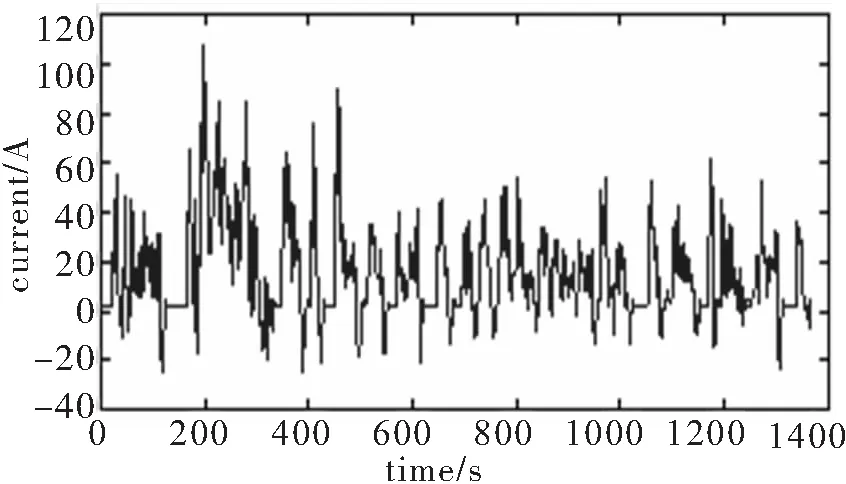
图12 UDDS工况下的电池电流
Fig.12 Battery current profile based on UDDS drive cycle test

将UDDS工况下电动汽车锂电池组的电流、电压数据导入到在Matlab中，分别应用EKF和AEKF算法对电池的SOC进行估计，最后将所得的估计结果与Advisor提供的参考SOC值进行比较，实验仿真对比如图13，SOC估计误差如图14、15所示。

由图13可得，由于UDDS工况下电流波动较大，EKF算法的估计误差明显偏大，最大时可达到5.1%.而AEKF算法的估计效果较好，估计误差在2.1%以内。相比EKF算法，AEKF无论是在收敛速度还是跟踪性能上都具有很大的优势，估计效果明显优于EKF，也说明通过新息序列不断更新测量误差协方差和系统噪声协方差，可以增强AEKF算法在复杂工况条件下对不确定扰动的适应能力。

图13 EKF和AEKF的SOC估计曲线
Fig.13 Battery SOC comparison based on EKF and AEKF

图14 EKF算法的SOC估计误差曲线
Fig.14 SOC estimation error curves with EKF

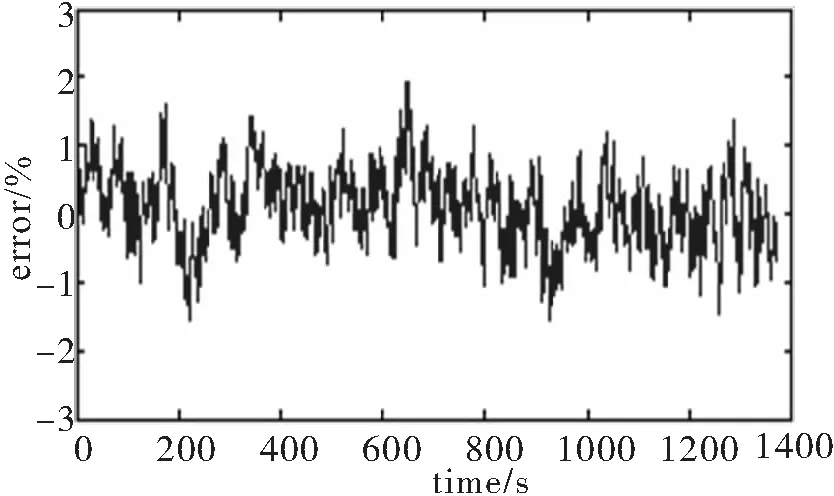
图15 AEKF算法的SOC估计误差曲线
Fig.15 SOC estimation error curves with AEKF

4 结论

针对电动汽车BMS的SOC估计问题，本文提出了一种较实用的自适应扩展卡尔曼滤波算法。首先，建立二阶RC等效电池模型，辨识模型参数，并通过仿真实验，验证了所建立的电池模型可以很好地模拟目标电池的动静态工作特性。然后，介绍EKF和自适应协方差匹配算法，对AEKF算法实现SOC估计的过程进行了理论推导。最后，设置仿真实验，通过对比分析，验证以上SOC估计策略的可行性和精确性。实验结果表明，AEKF算法可以根据误差和噪声的变化自动调整卡尔曼滤波增益，对白噪声和误差具有很强的抑制能力，使SOC估计更加稳定精确，适合对工况复杂的电动汽车锂电池进行SOC估计。