关注几何模型渗透 发展几何直观能力

范冰珊

[摘要]在小学阶段，有效地运用几何直观这个手段，可促进学生形象思维与数学抽象知识之间的融合，从而发展学生的几何直观能力，提升学生的数学素养。几何模型有很多种，在小学数学教学中常用的有数轴模型、线段图模型与面积图模型。

[关键词]几何模型;几何直观;数轴;线段图;面积图

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2019）35-0081-02

小学生的思维尚处于发展阶段，大多以直观形象思维为主，数学则是一门抽象性极强的学科，而“几何直观”正是有效搭建学生形象思维与数学抽象知识之间的桥梁。实践证明，借助几何直观这个手段，可以通过形象直观的图示将复杂的数学问题形象化，有效地促使空间维度的平面化，一定程度上降低学生解决问题的难度，有助于学生顺利地探索解决问题的思路，并成功地找到解决问题的路径。另一方面，借助几何直观手段，可使数学问题变得生动形象，从而促进学生展开丰富的联想与想象，有利于学生创造性思维的发展，提升学生解决问题的能力。因此，在课堂教学中，教师应渗透一些典型的几何直观模型，不断发展学生的几何直观能力，继而提升学生的数学核心素养。

一、渗透数轴模型，促进概念理解从抽象走向形象

数轴是初中数学的内容，但在小学数学教材中就已经开始逐步渗透。数轴在“数的概念”的理解上可谓是最佳的几何模型之一，巧妙运用数轴这个几何直观模型，能够有效促进学生在理解概念时能化抽象为形象，使学生对于数的认识更加直观、深刻，从而有助于发展学生的数感。

如，在教学人教版教材四年级下册“求小数的近似数”一课时，为了深刻揭示“求一个数近似值”的本质原理，笔者巧妙地运用了数轴来帮助学生理解“四舍五人法”的内涵。笔者先提问“2.54精确到十分位的近似数会是多少”，当学生利用正迁移的方法求出其近似数是“2.5”后，为了进一步促进学生对近似数本质的理解，笔者出示数轴（如图1），让学生通过观察数轴用数学语言表述为什么2.54的近似数是2.5，而不是2.4或2.6的缘由。借助数轴模型，学生能直观、形象地理解近似数的取值原理，体悟到数学知识有理有据的逻辑之美——仿佛每个数字都能开口说话，都能表达其特定的意义，从而促进数感的建立。

又如，学生往往对于取近似值时小数末尾的0要保留存在很多困惑，如果只是用直接告知的方式来教授，学生也只能是“只知其然，而不知其所以然”。为了实现学生对真正意义的建构，可以借助数轴这个直观模型（如图2），让学生明白近似数2.50与2.5之间的精确度是不一样。通过数轴模型，学生能明显地看到2.5的取值范围在2.45与2.54之间，而2.50的取值范围则在2.495与2.504之间，近似值2.50比2.5更为精确，从而直观感悟到“在取近似值时小数末尾的0不能去掉”的本质意义，有效地发展了自身的数感。

二、渗透线段图模型，促进数量关系从模糊走向清晰

当碰到一些信息条件比较隐蔽的数学问题时，学生常常无法正确分析出题中错综复杂的数量关系，导致错漏百出。因此，在课堂教学中，教师要借助线段图这个几何直观模型，培养学生通过数形结合的方式进行数量关系分析的习惯，促使学生对数量关系的分析更加清晰。

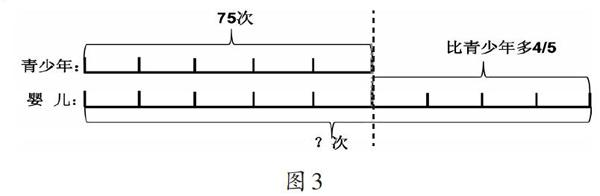
如，在教学人教版教材六年级上册“分数乘法”单元中的“解决问题”一课时，当创设情境并出示例题“人心脏跳动的次数随年龄而变化。青少年心跳每分钟约75次，婴儿每分钟心跳的次数比青少年多4/5。婴儿每分钟心跳多少次？”之后，部分学生受整数解决问题的负干扰直接列式为“75+4/5”，也有部分學生列式为“75x4/5”。这些错误都源于学生没能弄清楚青少年的心跳次数与婴儿的心跳次数的数量关系，如果只是停留在文字层面引导学生进行分析，显然是比较抽象的。为此，可以启发学生画线段图来分析题目中的数量关系。“对于这两个量，要先画哪个量的线段呢？”这是学生在画线段图时要弄清的第一个问题。首先要启示学生“把哪个量当作标准量，它就是单位‘1，就要先画哪个量”，于是自然唤起学生分析题意时要抓住题目中的关键句，即“婴儿每分钟心跳的次数比青少年多4/5”，从而发现了应该先画“青少年心脏跳动的次数”。而婴儿心跳次数就是比青少年的5份还多出了4份，也就是婴儿心脏跳动的次数是青少年心脏跳动次数的（ 1+4/5），从而画出线段图。如此，青少年心脏跳动的次数与婴儿心脏跳动的次数之间的数量关系通过线段图的呈现变得直观而清晰（如图3）。

借助线段图这个直观模型，将题目中内隐的条件直观化，能有效地促使数量关系从模糊走向清晰，让学生的思考找到了可支撑的媒介，从而提升学生的思维品质。这样不但有效地积累了学生的数学活动经验，而且降低了分数应用题的抽象度，使抽象文字得以清晰呈现。

三、渗透面积图模型，促进解题思路从内隐走向外显

借助面积图能将一些表述抽象的文字信息具体形象化，促进学生解题思路从内隐走向外显，使得问题解决思路可视化。根据教学问题与学生实际思维的需要，恰到好处地运用好面积图模型，能有效提升学生解决问题的能力，发展学生几何直观水平。

如在解决“一张长方形彩纸长13分米、宽6分米，这张纸可以剪几个边长为2分米的正方形？”这道题时，学生往往会直接用大面积除以小面积，即列式为“13x6÷22'，算出“19.5个”，并用退一法得出“19个”。这样的想法单从文字层面上看，学生完全感觉不到是错误的。面对学生这样的“想当然”，教师要巧妙地引发学生的认知冲突：“到底一共可以剪多少个小正方形？大家不如动笔画一画。”于是学生一边画图（如图3）一边分析，就会很快发现之前解法的错误所在，正确的解法应是“13÷2-6（个），6÷2=3（个），6x3=18（个）”。通过面积图，可以让内隐的解题思路外显，即当长方形的长、宽不是小正方形边长的倍数时，是不可以用“大面积除以小面积”的思路来解决的，从而有效地提升了学生的数学思维品质。

运用面积图这样的几何模型，能让抽象的算理可视化，有效避免数学运算的枯燥与抽象，在一定程度上让学生感悟数学运算不只是纯技能的程序化操练，每个数字与运算符号都是生命的象征，是一种数量关系的符号表达。

一言以蔽之，几何直观模型除了以上介绍的三种外，还有连线模型、直条模型等。而学生的几何直观能力也不是一朝一夕就能形成的，是要经过漫长的、有意识的渗透与训练。因此，教师要有意识地让学生经历从文字语言到图形语言，并从图形语言提升到符号语言的全过程，致力于将抽象的、模糊的、内隐的数学知识转化成直观的、清晰的、外显的数学现象，有效地发展学生的几何直观能力，继而提高学生的数学综合素养。

（责编 罗艳）