基于递推最小二乘的三轴磁强计在线自校正方法

向奉卓， 李广云， 王 力, 王安成， 俞德崎

(1.信息工程大学 地理空间信息学院，河南 郑州 450001;2.信息工程大学 数据与目标工程学院，河南 郑州 450001)

0 引 言

随着科技的进步和经济的快速发展，人们对位置服务的需求越来越高。而传统的导航定位设备[1,2]大都成本高昂、结构复杂，不利于技术推广。近年来,微机电系统(micro-electro-mechanical system,MEMS)的快速发展，使低成本、低功耗、小体积的MEMS姿态传感器[3,4]越来越多地用于民用导航领域。在低成本的航姿参考系统中，航向信息主要通过电子罗盘获取[5，6]，其核心原件就是三轴磁强计，磁强计通过测量地磁矢量信息来获取航向。而在实际的应用中，周围的干扰磁场会对其产生严重影响导致所测量的航向值含有较大的误差，不能直接用于导航定位[7]。因此有必要对磁强计进行误差校正以提高其工作性能、获取可靠的航向信息。文献[7]提出了基于递推最小二乘的罗差校正方法，需要已知磁倾角和初始航向角的情况下才能完成，实用性较差。文献[8]采用基于无磁转台的误差分离标定方法，需要依靠外界参考信息，对实验条件要求较高。文献[9～11]提出的椭圆拟合算法，主要针对载体在二维平面下运动航向的误差补偿不适用于三维空间中的载体航向的修正如飞行器导航。文献[12]提出的基于拓展卡尔曼滤波器实时自校正算法，需要确定合理的初始条件，且算法复杂。

①生产管理单位提前进厂费，不应计入“建筑安装工程投资”，按《编规》规定，它是指在工程完工之前，为生产筹备发生的人工费、办公费等费用，与生产职工培训费性质类似，笔者认为应计入“其他投资”，形成交付使用资产—递延资产。

本文提出一种基于递推最小二乘的误差在线自校正方法。方法以椭球假设[13,14]自动校正方法为基础，利用原始的磁力计数据由递推最小二乘算法实现椭球方程系数在线辨识，进而求得误差校正参数。实验结果表明该方法具有较高的实用性和可靠性，能有效校正硬磁和软磁效应引起的误差。

1 校正基本原理

1.1 误差模型

三轴磁强计的工作原理是通过测量理想环境下地磁矢量在三轴的分量来获取载体的航向信息。而在实际应用中，由于受到周围环境中硬磁和软磁效应的影响，磁强计的测量会产生较大误差。其中硬磁效应主要是指载体的硬磁材料被磁化后产生的固定磁场，不随传感器位置变化而变化，可看作常量。软磁效应指载体的软磁材料被磁化后产生变化的磁场，软磁误差的大小与传感器的姿态变化及周围元器件的工作状态都有关系。假定理想条件下，地磁矢量在磁强计坐标系中表示为C=[CxiCyiCzi]T,受到软硬磁效应影响后传感器的测量值为M=[MxiMyiMzi]T,根据Poisson模型[15]将两者之间的关系表示为

(1)

式中 矩阵R=(Rij)3×3为软磁干扰矩阵，在软磁效应下，该矩阵满足对角占优原则，即对角线上元素接近1，而非对角元素均较小接近零[15,16]。矩阵b=[bxbybz]T为硬磁效应对三轴产生的固定影响。

基于上文所提出的四模交叉谐振器结构,本文设计出了对应的四频带带通滤波器。滤波器原型结构如图3所示,它由两个伪交指级联形式耦合的四模交叉型谐振器组成,其中一些微带线采用扭曲形式布线以减小电路板尺寸。

由式(1)知，求解软磁干扰矩阵R和硬磁干扰矩阵b是实现磁强计误差校准的关键，地磁矢量测量值校正模型可写为

(2)

根据式(8)中参数辨识模型和递推最小二乘算法原理，误差在线校准的实现步骤如下：确定递推初值，为提高椭球曲面方程系数辨识的精度，先将获取到的大于所需辨识参数个数(A1～A9)的L组数据，利用最小二乘的方法求得参数的估计值(0)和协方差矩阵P(0),并作为递推初值。令

1.2 椭球假设

在理想情况下，在同一位置旋转磁强计所测得的磁矢量变化轨迹在三维空间中应该形成一个圆球面。而实际应用时，由于受到软硬磁场的干扰所得磁向量变化轨迹为一个椭球面。根据式(1)整理为二次型可得

加强项目谋划和资金争取。突出产业发展等重点领域，分类分项谋划一批重点项目。认真研究梳理国家、省各项政策，建立上级政策（项目）争取指导目录、信息对接、月度例会、跟踪协调和督导问效等工作机制，加强协调对接，及时申报争取各类政策（项目）资金支持。

MTM=(RC+b)T(RC+b)

可认为递推过程结束。以上求解椭球曲面方程系数θ的过程也间接完成了误差校正参数的在线辨识。根据校正模型，完成磁强计的误差校准。

(3)

式中 由于R为软磁干扰矩阵满足严格对角占优，所以RTR为正定阵，MTM为一个椭球面，则三轴磁强计测量值[MxiMyiMzi]T应该满足椭球曲面方程

我们的目的是得到一个多处理器的作业调度序列使得产生的总效用最大化，但这个问题是NP-hard问题[3]，因此，我们考虑能否找到一个具有最优解的某些性质的解。首先考虑只有一个处理节点的简单情况，我们将作业集合划分为若干子集，使得算法得到的调度序列最优解形式上均为依次调度T1T2…Tm这m个子集中的作业。因此，我们要设计一个产生某个序列的调度算法，满足以下目标：（1）算法序列应产生接近最佳值的值；（2）如果存在上述划分，算法序列应该与之相兼容。此时，算法序列在子集层面上与最优调度序列保持一致。

由式(2)给出的误差模型，C=[CxiCyiCzi]T应满足球面方程，令Q=R-1，转化为二次型

(4)

式中θ=[A1A2A3A4A5A6A7A8A9]T，n(i)为随机测量噪声。

1.女：一伟拜上关云长（一首拜上关云长），拜上云长保江山，若押保的荆州府(若你保得荆州府)，五虎上将押头名（五虎上将你头名）。

P(i)=[I-K(i)mT(i)]P(i-1)

=MTQTQM-2bTQTQM+bTQTQb=r2

(5)

式中r为与当地地磁强度相关的未知常数，其大小仅影响误差补偿后地磁矢量的模长，本文通过地磁矢量投影到各坐标轴分量的比值来解算航向，因此r大小对最后的航向解算并无影响。

假设Q为对称阵且满足对角占优，则将式(5)展开与式(4)对比可得

(6)

式中k为未知常数。

求得Q和b后，可按C=Q(M-b)完成对测量值的误差补偿。则误差校正模型式(2)中未知参数求解问题转换为拟合椭球曲面方程系数求解，本文将通过递推算法实现椭球曲面方程系数的在线辨识，进而求解误差校正参数。

2 在线校正实现

递推最小二乘算法能够按照采样的时间顺序，每获得一组新的磁场数据就修正一次椭球方程系数的估计值，随着时间推移最后完成椭球曲面方程系数辨识，具有每次计算量少、占用内存小、能够实现系数在线辨识等优点。

③对水泵各项指标数据，在现场测得几项重要数据后依据水泵的使用情况、使用时间及当地水质情况，对照水泵型号表才能正确取得。采用水量实测的方法现场测得水泵每小时的实际出水量，采用三相异步电动机依据电流表的实测电流量除以2得到功率的方法获得水泵的实际功率，通过水泵说明书或水泵扬程标牌及询问管理人员等方式获得水泵扬程。

为求取椭球方程系数θ，可将式(4)化为

z(i)=mT(i)θ+n(i)

(7)

式中

对待敷衍搪塞的采访对象，不妨大小合适地扣一扣帽子，一市党报，总不至于该拿热脸去贴谁的冷屁股。刚干记者那会迟恒吃过顾虑拘谨的亏，灰溜溜地回部里告诉主任，主任不悦，打电话给市某局长，有反映你们局“五创提质”太弄虚作假，你们是不是来报社说一下情况。他起身吩咐迟恒守着，人来了就说我在楼上有事，让他等。局长来了，也能耐着性子等。这课上得生动活泼，迟恒受益匪浅，后来在采访调查几个单位的问题时，有单位领导出面遮掩，很客气地说某事要向迟记者汇报，迟恒就整个儿悟出他这个迟记者完全可以无级胜有级，练了段时间，胆儿粗了，脾气长了，现在基本上能随需要调整态度。

(8)

对上述矩阵12参数的求解的方法大都需要外界的参考基准，特定的实验环境条件从而限制校正方法的推广与使用[4,8]，而基于椭球假设的自校准方法不依靠外界设备，仅依靠获取的磁强计数据即可实现对校正参数的求解，适用于多种环境下的误差校正。

K(i)=P(i-1)m(i)[mT(i)P(i-1)m(i)+1]-1

(9)

CTC=(M-b)TQTQ(M-b)

(10)

得到

为验证本文提出算法的有效性，采用以HMC5883L磁阻传感器为核心的电子罗盘作为实验仪器，通过手持磁罗盘旋转不同的姿态来获取传感器在不同方位的三轴磁场数据。具体实验步骤如下：

(11)

迭代计算式(9)～式(11)，直到待辨识的参数估计值变化不大ε时即满足关系式

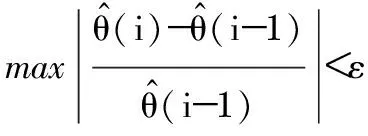
(12)

=CTRTRC+2bTRC+bTb

3 实验与结果分析

联合国教科文组织(UNESCO)在1997年3月推出的“国际教育标准分类”中将高等职业教育与普通高等教育并列划分[1]．高等职业教育不是从属于普通高等教育的更低层次的组成部分，而是一种独立存在的教育类型．高等职业教育与普通高等教育不同的培养目标从根本上决定了它们在选拔方式、培养目标以及学习内容等方面存在明显差异．

1)为了尽可能采集到传感器在各个方向下磁场数据，使获得的原始数据尽可能在球面均匀分布。实验中采用手持传感器进行“8”字晃动来获取数据，共采集1 000组数据，导出数据并绘图，如图1所示。图中记录了通过变换姿态采集数据时的磁场轨迹，可以看出磁场数据分布类似一个椭球面。

图1 校正前磁强计测量值

2)选取采样数据中的前10组，根据最小二乘算法求取递推初值和协方差矩阵P(0)。

从当前的实际情况来看，现有的乡村生态旅游经营形式还比较单一，乡村生态旅游产品还存在同质化的特征。这种服务形式，也是无法满足消费者的个性化需求的。因此，在实际情况中，乡村生态旅游经营者就应该积极地创新服务形式，突出当地的特色，积极地创建一些体验价值高的乡村生态旅游产品。另外，乡村生态旅游者也可以积极地采取各种有效措施去深入地挖掘社会中各个旅游群体的实际需求，从而为他们提供具有针对性、个性化的服务。

3)采用文中提出的递推最小二乘算法，根据式(9)～式(12)利用获取的磁场采样数据实现对椭球方程系数的在线辨识。由得到的椭球曲面方程系数将磁场数据拟合得到一个椭球面，如图2所示，图中可以看出由于受到硬磁和软磁效应的干扰，磁强计输出值发生了严重畸变，拟合椭球的球心并不在原点发生了偏移，整个球体在三维坐标系下产生了微小的旋转，球体三轴的长度发生了不同程度的缩放，使圆球变成了椭球。

图2 校正前的地磁拟合球面

4)由步骤(3)求得的椭球方程系数，按照式(6)中椭球曲面方程系数与误差校正模型参数之间的对应关系，求解校正模型参数。在本实验条件下求得误差校正矩阵Q和b

采用直接在家具成品上测试时，要选取家具中的主要面层，要求可检测面部位表面平整，无鼓泡、划痕、褪色、皱皮等缺陷。

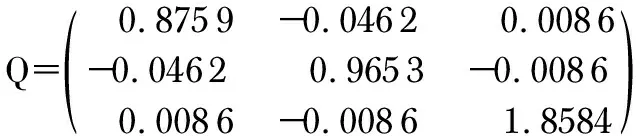
b=[-27.295 6 -12.923 7 -4.932 7]T

党的十九大对乡村振兴战略提出了“产业兴旺、生态宜居、乡风文明、治理有效、生活富裕”的20字总要求。2018年是实施乡村振兴战略的开局之年。“乡村振兴战略”如何破题？

对原始测量值进行误差校正，画出校正后磁场数据分布，如图3(a)所示。按照步骤(3)中方法对校正后的数据进行拟合并画出拟合的球面，如图3(b)所示。从图中可以看出根据误差校正模型对磁场数据的误差校正效果比较明显，拟合球体的球心基本位于原点，三轴的长度也近似相等，对产生的微小旋转也进行了一定程度的修正。

图3 误差校正

在理想条件下，定点处地磁矢量模长相等，因此，传感器同一位置变换不同的姿态所获取的磁场数据应该拟合成一个圆球面，根据圆球曲面上任意一点到球心距离相等，所以曲面上各采样点处磁场强度大小应该相近，不存在大的数据波动。以原始测量数据磁场强度均值为基准，求取误差标准差作为校正效果评定指标。分析对比校正前后各采样点磁场强度大小的变化，可知，误差校正前采样点磁场强度大小波动幅度较大高达67.112 8，误差标准差为15.828 7，经过误差校正的磁场强度大小波动幅度明显减小最高为14.064 8 ，误差标准差为6.345 1 。结果表明，利用基于递推最小二乘的误差校正方法可以有效地校正软磁和硬磁效应对测量数据产生的误差。

4 结 论

本文所设计的基于递推最小二乘的磁强计误差校正方法能够完全由传感器自行完成误差的计算与校正，具有方便、有效、实用性强、能够在线校正等优点，适用于无外部参考基准下三轴磁强计的误差自动校正。