基于多维标度的非线性模拟电路故障诊断方法*
贺开放, 李 兵, 何怡刚
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引 言
模拟电路的故障诊断已经成为了电路领域的一大重要分支[1]。特别是进入21世纪以后,伴随着生产工艺的提高,被测电路的可及节点数减少,增大了对其故障诊断的难度,因此,模拟电路故障诊断技术成为了研究的热点[2]。传统的故障诊断方法有故障字典法[3]、元件参数辨识法[4]、故障验证法[5]等,以及现代数据处理技术,如小波变换[6,7]、支持向量机[8,9]、神经网络[10]主成分分析(principal component analysis,PCA)[11]等,这些方法极大地促进了故障诊断技术的进步。虽然小波变换可以充分包含故障信息,但在实际的应用中小波变换易受噪声影响,精准度依赖于母小波的选择。神经网络存在算法收敛速度慢、容易陷入局部最优、受网络结构复杂性和样本复杂性的影响较大等缺点,需要不断地调整过程参数。PCA方法是一种线性方法对于复杂非线性系统,可能会丢失系统所包含的重要非线性信息[12]。该方法在一定程度上解决了模拟电路中的容差问题以及非线性问题,但是在实时故障诊断的应用过程中,这些方法普遍存在通用性差、网络收敛速度慢、网络设计结构理论不够成熟等缺点。
本文采用统计学中多维标度(multi-dimensional scaling,MDS)[13]方法,利用其故障特征提取和分类能力,且所需样本小,将其应用于模拟电路故障诊断领域。以模拟电路的阶跃响应为例,通过对输出波形上的6个采样点进行MDS分析提取出故障特征形成新的样本集,再进行聚类,实现模拟电路的故障诊断。本文方法能够充分利用模拟电路不同故障间的输出响应差异信息来对多种故障类型进行分类,能够实现故障检测及定位,具有算法简单、准确率高的特点。
1 MDS技术
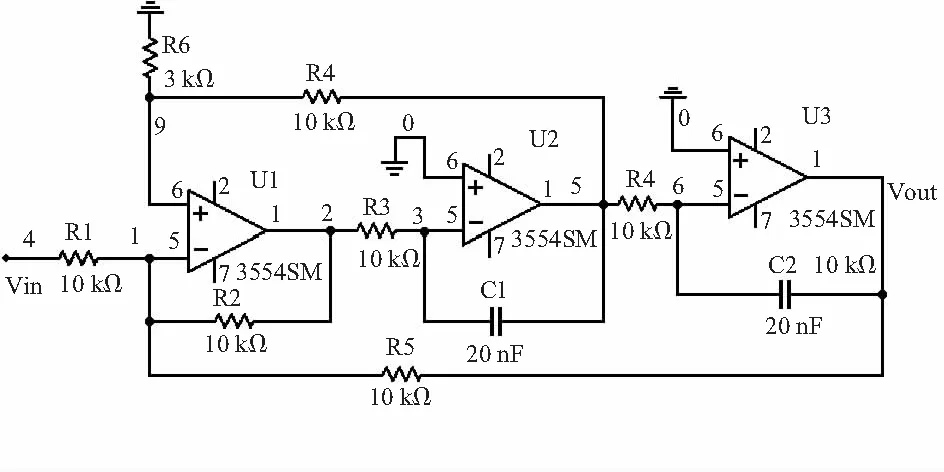
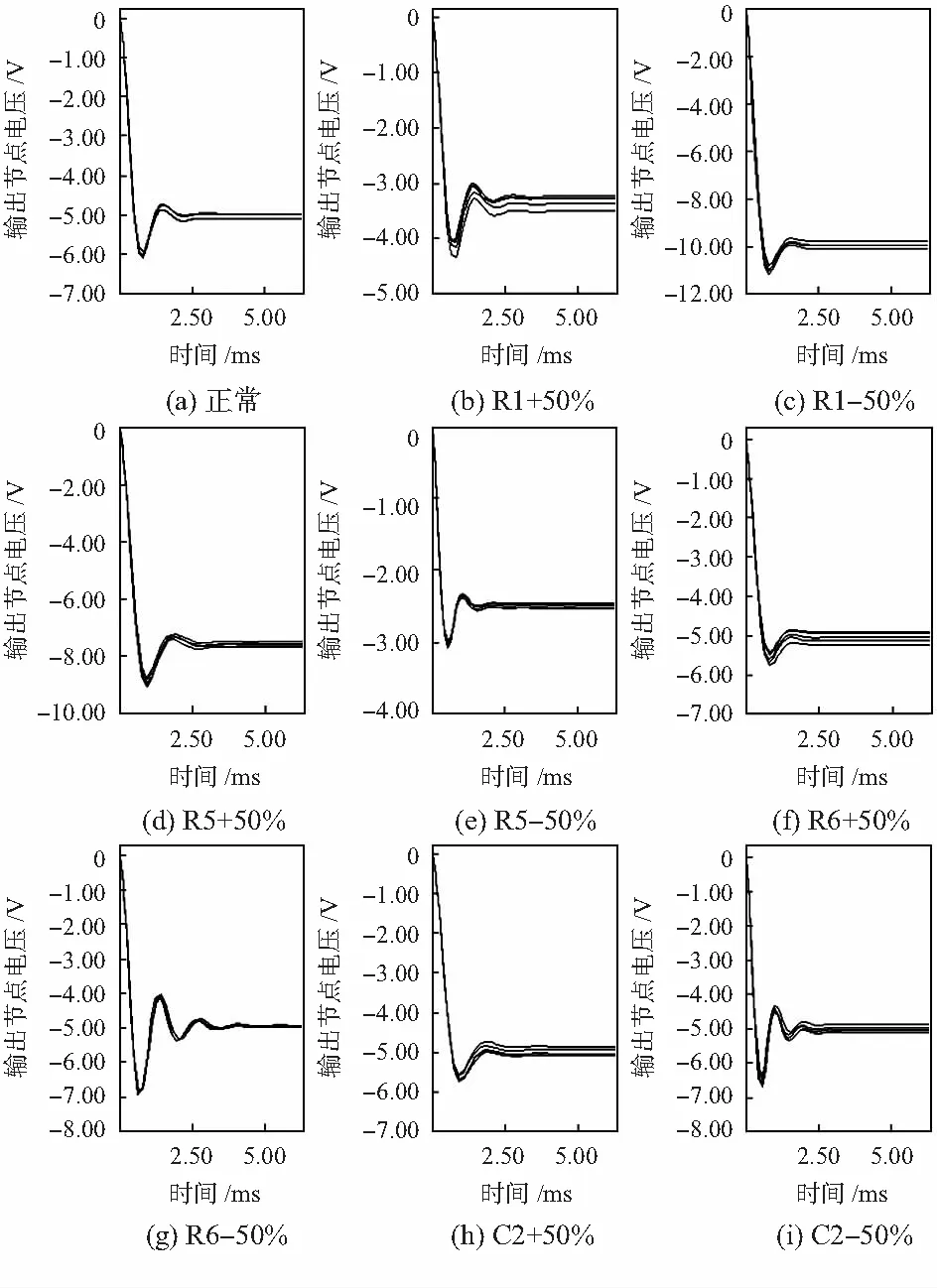
MDS[13]技术的基本思想是用低维空间Rk(k 在MDS中实体i和j之间的相异性dij用欧氏距离来表示,由各实体间的相异性dij构成相异性矩阵D。构造多维空间上点的坐标矩阵用Xn×k表示,n为坐标点的个数,k为坐标点的维数,X的每一行对应一个坐标点i的k维坐标,多维空间上坐标点i和坐标点j的欧氏距离用ij(X)表示。MDS技术利用各实体间的相异(似)性来构造多维空间上点的相对坐标图时应使得相异性dij与ij(X)尽可能地接近,用dij≈ij(X)表示,其接近程度在MDS中用胁强系数(STRESS)的大小来衡量。胁强系数定义为 (1) 在模拟电路故障诊断中,考虑到不同的故障点会有不同的数据特征,故障点间在多维空间中会存在一定的距离,因此,可以根据距离的大小来进行判断和分类。MDS故障诊断算法是一种在低维空间中展示“故障点之间距离”的数据结构的多元数据分析技术,利用样本向量间的欧氏距离表示故障点间的相异性。为了更能显示出不同故障类型之间的相异性,根据电路输出波形的特点,发现输出波形在0~2 ms之间变化较大,在2 ms之后趋于稳定,因此,本文在采集数据时选择在0~2 ms之间进行采样。能够更好地突出各个输出波形的特征,使故障诊断率更高。MDS实现故障诊断的具体步骤如下: 1)根据距离阵数据,计算出bij。 设模拟电路的故障特征构成原始数据样本集Yn×p(其中n为样本数目,p为故障特征数目)。矩阵表示为Yn×p=[Y1,Y2,…,Yn]T,则Yi的坐标记作Yi=[Yi1,Yi2,…,Yip],i=1,2…,n。 定义一个n×n阶的矩阵D=(dij)n×n,如果满足条件:D=DT;dij≥0,dii=0,i,j= 1,2,…,n。则称距离阵D为广义距离阵,dij为第i点与第j点之间的欧氏距离,有 (2) 设k维空间中的n个点的矩阵表示为Xn×k=[X1,X2,…,Xn]T,则Xi的坐标记作Xi=[Xi1,Xi2,…,Xik]。在MDS技术中称Xn×k为距离阵D的一个拟合构图,k维空间中的距离阵为D的拟合距离阵,要求与D尽可能的接近。其中 (3) 则 (4) 2)根据bij构造出X的中心化内积矩阵B (5) 3)计算矩阵B的特征值和特征向量并选取主要的特征值和与之对应的特征向量。 设B的特征值为λi与之对应的特征向量为ei,其中r个最大的特征值为λ1≥λ2≥…≥λr>0对应的特征向量为e1,e2,…,er,记Γ=[e1,e2,…,er]是特征向量组成的矩阵。其中r的取值有两种确定方法:a.事前确定好r=1,2或3;b.通过计算前r个大于零的特征值占全体特征值的比例δ来确定,即 (6) 式中δ0为预先给定的变差贡献比例。 4)根据式(8)计算Xn×k,得到r维拟合构图,令Λ=diag(λ1,λ2,…,λr),那么 B=XXT=ΓΛΓT (7) (8) 计算出了所需要的降维后的数据集,可以更好地对不同类型的模拟电路故障点在低维空间内进行聚类。 为了验证上述诊断方法的有效性,本文的诊断电路选自ITC' 97[15]国际标准电路中的CTSV滤波器(continuous-time state-variable filter),如图1所示。 图1 CTSV滤波器(ITC 97) 各元器件的标称值在电路中都已标出,输入节点为Vin,输出节点为Vout。在仿真实验中,设置电阻器和电容器的正常容差均为标称值的±5 %,由于模拟电路中单故障出现的概率约占总故障的80 %~90 %,因此只考虑电路中无源元件发生单故障的情况。设元件偏离其标称值的±50 %时为故障状态。考虑到各元件参数值的变化对电路的输出影响的大小不同,对待测电路进行灵敏度分析,针对本文电路的特点,选择灵敏度较高的元件R1,R5,R6,C2作为故障元件,其中偏离标称值+50%的故障状态记作R1+,R5+,R6+,C2+,偏离标称值-50%的故障状态记作R1-,R5-,R6-,C2-。因此本文只讨论R1+,R5+,R6+,C2+,R1-,R5-,R6-,C2-和正常情况共9种状态,所设置的故障类型如表1所示。 表1 电路故障类型 通过电路仿真软件Multisim10.0按照表1对电路的正常状态和故障状态分别进行仿真,电路某一时刻只发生单故障,且其他元件在其容差范围内随机变化。正常状态下所有元件在其容差范围内变化。给CTSV滤波电路施加幅度为5 V的阶跃信号,然后从输出节点Vout处采集到阶跃响应曲线。在阶跃响应曲线的前2 ms内均匀采集6个数据点,构造具有6个分量的故障特征向量Yi=(Yi1,Yi2,Yi3,Yi4,Yi5,Yi6)。对每种状态分别进行30次Monte-Carlo分析,共获得270(30×9)个向量样本。图2给出了9种状态的部分阶跃响应曲线(每种状态5种样本)。 图2 CTSV滤波电路在9种状态下的部分阶跃响应曲线 在MATLAB 2014仿真环境下对采集到的故障样本运用本文提出的方法进行仿真。经过处理后得到了输出节点Vout采样数据的特征投影如图3(a)所示,从仿真结果可以看出,本文所提出的方法完全可以对各个故障类型进行识别和成功聚类,取得了理想的结果。 为了对比本文方法与PCA方法的性能,运用此方法对本文模拟电路的同样数据进行故障诊断,得到上述方法的聚类结果如图3(b)所示。 图3 MDS,PCA聚类结果 由图3可以看出,PCA方法与MDS方法相比,故障R6+和C2+的聚类靠的太近不能区分清楚,而MDS方法对每种故障类型的聚类区分的更加清楚。最后计算准确率、平均诊断时间和STRESS,结果本文方法在准确率各故障类型下均为100%,而PCA在R6+故障下,诊断率权为96.77%、诊断时间和STRESS(本文为3.53%,PCA为47.76%)上与其他方法相比均有一定的提升,尤其是大大缩短了诊断时间(0.097s),而PCA为0.465s,这将十分有利于模拟电路的在线诊断,利于其实际应用。 本文提出了一种基于MDS算法的模拟电路故障诊断新方法,与其他方法相比,该方法具有算法简单、所需测量节点少、可以实现快速故障检测及定位、且具有较高准确率的特点。2 MDS故障诊断方法
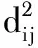
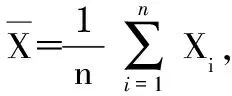
3 仿真与结果分析


4 结 论

