多梁式钢-混组合弯箱梁桥荷载横向分布系数计算分析

章晗 丁汉山

（东南大学土木工程学院 南京211100）

引言

弯箱梁桥是一种广泛应用的桥型，一直以来主要运用在城市立交桥的匝道中，近年来随着施工技术的进步、国家经济实力的提高，设计者对道路线型的要求也越来越高。弯箱梁桥不仅能够很好地适应地形地貌和道路线型，而且造型优美、富于变化。因此人们对弯箱梁桥的研究越来越重视。

桥梁设计主要问题之一是准确地计算桥梁结构在外荷载作用下的内力，为了方便而准确地计算桥梁内力，通过荷载横向分布系数不仅能够将空间问题转化为平面问题，而且能大大简化计算的工作量。目前，常用的曲线桥梁横向分布计算方法主要有梁系理论、板系理论、梁格理论等等。针对曲线桥梁横向分布系数的计算，李国豪[1]基于单根曲梁的微分方程，计算出相应变形，然后对横截面建立力法正则方程求解截面未知力，从而计算影响线；姚玲森[2]基于比拟正交异性板法，提出曲线梁的实用计算方法；Leon-hardt和Homberg假定桥梁结构为主梁与横梁处于弹性支承梁关系的格构，按照骨架的力学性质来求解。

上述理论对横向计算均较精确，本文在梁系理论基础上，对钢-混组合中等跨径弯梁桥进行横向分布计算，并进行参数化分析，以得到相应的变化规律。通过对钢-混组合弯桥的横向分布计算分析并与有限元计算结构对比，得出相关变化规律，希望对工程实践具有一定参考意义。

1 钢-混组合弯梁桥的刚接梁法

1.1 单根组合截面曲梁位移的结构力学解

如图1所示，在竖向荷载R＝1或扭矩T＝1作用下，结构由同一种材料组成的主梁计算截面θz＝θp处的挠度及转角计算公式，根据文献[3]如下：

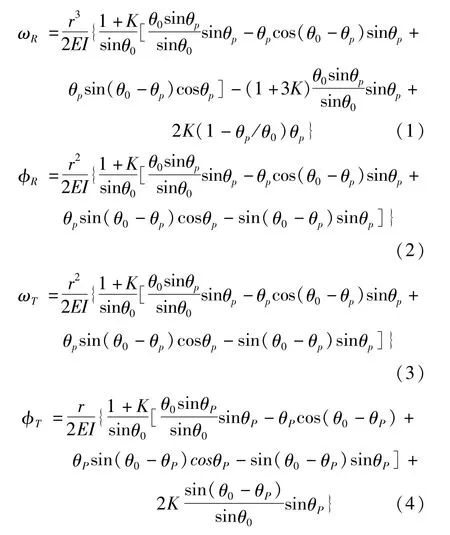
式中：ωR为单位竖向荷载在计算截面产生的挠度；ωT为单位扭矩在计算截面产生的挠度；φR为单位竖向荷载在计算截面产生的转角；φT为单位扭矩在计算截面产生的转角；为主梁的弯扭刚度比；I为主梁的抗弯惯矩；θ0为曲线梁桥的圆心角；θp为荷载作用截面位置；θz为计算截面位置；θp＝θz为荷载作用截面即为计算截面。

但是对于钢-混组合结构来说，曲线梁的单梁位移计算则不能简单套用上述公式，必须进行截面换算。根据文献[4]和文献[5]，组合结构抗弯惯性矩和抗扭惯性矩GJ计算如下：抗弯惯性矩的计算原则是将混凝土换算成钢材，遵循保持组合箱梁截面混凝土顶板合力大小不变、合力作用点位置不变以及不改变截面的中性轴，改变混凝土顶板宽度而不改变其高度：

式中：b为混凝土顶板实际宽度；b′换算之后顶板宽度；αE为钢材弹性模量与混凝土弹性模量之比；Es为钢材弹性模量；Ec为混凝土弹性模量。

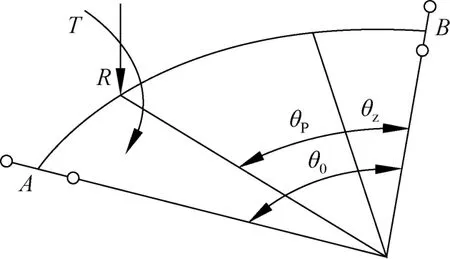
图1 单根曲线梁计算图示Fig.1 Calculation diagram of single curved beam

将截面换算之后，抗弯惯性矩EI就按换算截面计算，材料为钢材，同时还需考虑内横梁对抗弯惯性矩的影响，参考文献[6]中相关内容。同理，组合截面抗扭惯性矩GJ的计算也必须进行截面换算，基本原则同上，只将混凝土顶板厚度进行换算，之后按钢材和换算后截面计算：

式中：h为混凝土顶板厚度；h′为换算之后顶板厚度。

1.2 曲梁系的力法正则方程

1.基本假定

（1）将具有n片梁的多梁式钢-混凝土组合小箱梁桥的荷载横向分布，可将其在各梁间的中部切开，代之以梁间多余竖向剪力和弯矩等，由于纵向剪力和轴力相对竖向剪力十分小，故可以忽略它们的影响。如图2所示。

（2）对任一梁i，可以根据每片梁所受的力，建立典型的力法方程，分别计算出方程的各项柔度系数，求解各个多余未知力即可得荷载在各个梁的横向分配。如图2所示。各片曲线梁在切口两侧在单位力作用下的位移不同，图3、图4加上标加以区别。

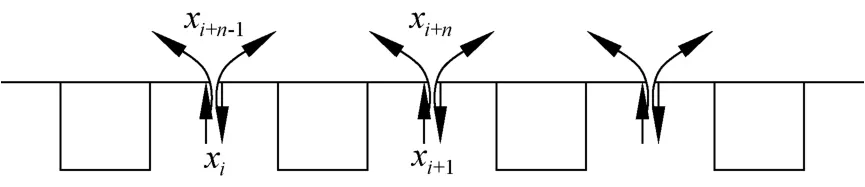
图2 组合小箱梁截面内力Fig.2 Sectional internal force of small box girder

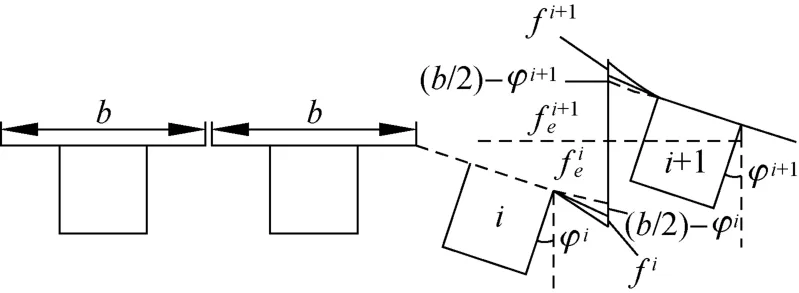
图3 缝端单位剪力作用下的挠度与转角Fig.3 Deflection and rotation diagram under the action of unit-sheer

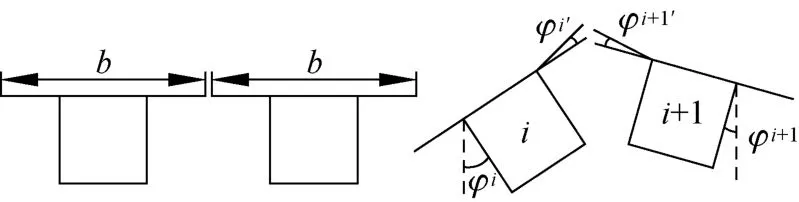
图4 缝端单位弯矩作用下的挠度与转角Fig.4 Deflection and rotation diagram under the action of unit-moment

2.力法方程

根据力法原理及图2、图3和图4，建立以竖向剪力、弯矩为赘余力的力法方程为：

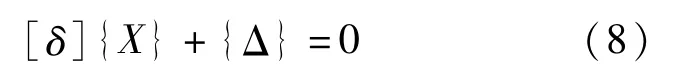
式中：[δ]为柔度系数矩阵；｛X｝为赘余竖向剪力和弯矩矩阵；｛Δ｝为外荷载引起的位移矩阵。

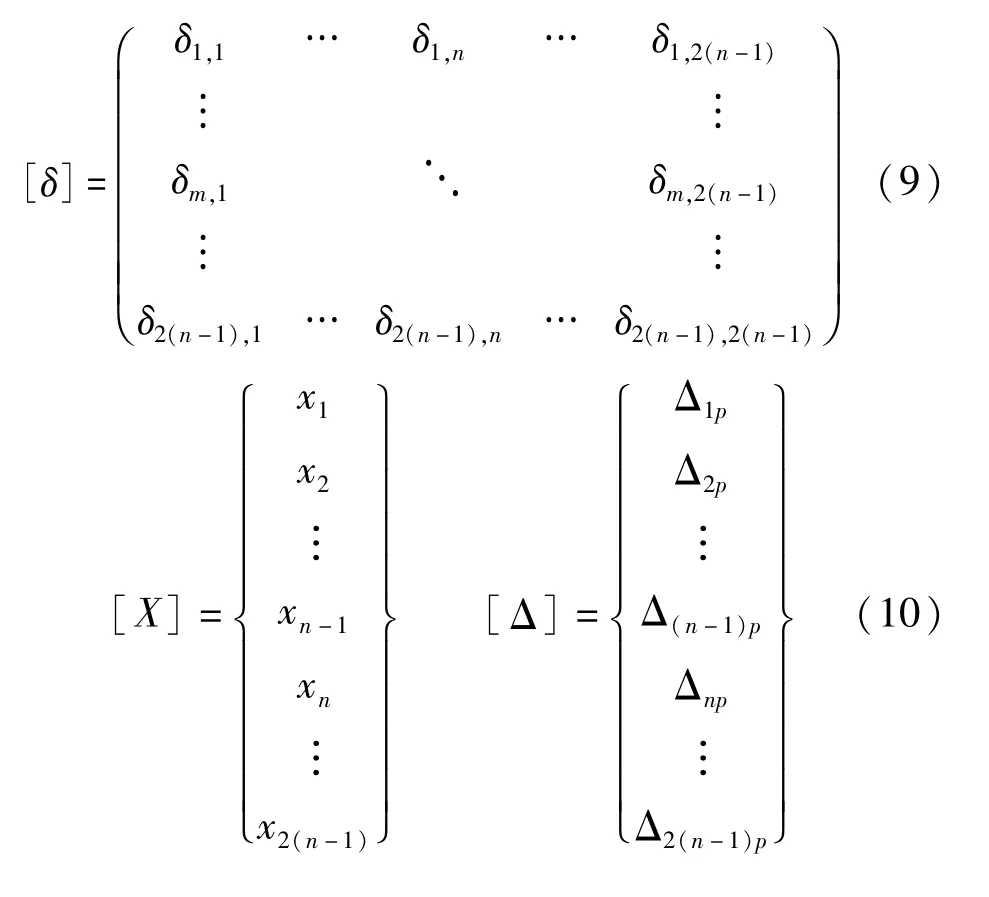
柔度系数计算如下：

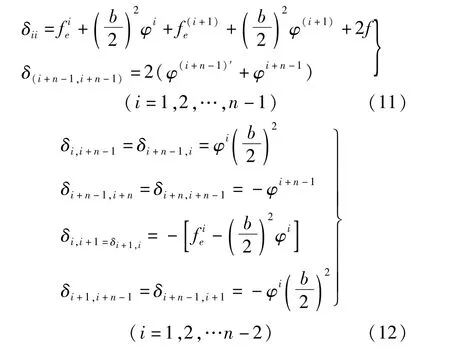
其余δij＝0。

j为外荷载P作用位置，则有：

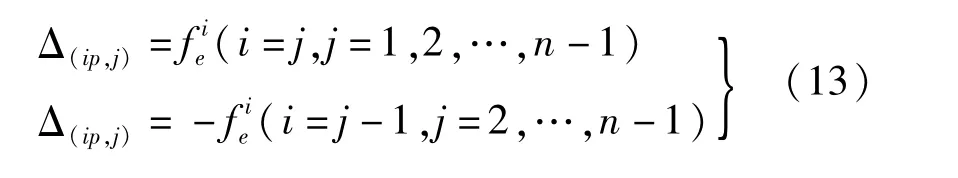
其余Δ（i+n-1）p，j＝ 0。

式中：δi，j为荷载xj方向作用单位荷载产生沿荷载xi方向的变形（挠度或转角）；为第i号曲梁在单位荷载或力P作用下产生的挠度；f为单位竖向荷载作用在小箱梁悬臂端部时在该处产生的弹性挠度，由于各片梁曲率半径和跨径相接近可忽略其影响；φi为单位扭矩作用于第i号小箱梁截面扭心时引起的截面扭转角；φi′为第i号小箱梁悬臂端部作用有单位弯矩在悬臂端部产生的弹性扭转角，同上忽略曲率半径和跨径影响；f′在箱梁悬臂端部作用有单位弯矩时在悬臂端部产生的弹性挠度或在小箱梁端部作用有单位竖向荷载时在悬臂端部产生的扭转角。

1.3 荷载横向分布影响线

解出上述力法方程为即可得到各切口的未知力，由此便可计算各主梁分配荷载的横向分配系数。由第i行的运算，可得第i号梁的竖向荷载分配系数：

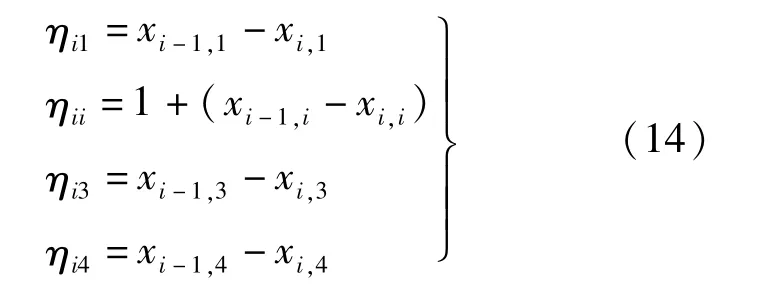
式中：ηi1为单位竖向荷载作用在1号梁对i号梁产生的竖向反力；ηii为单位竖向荷载作用在i号梁对i号梁产生的竖向反力；ηi3为单位竖向荷载作用在3号梁对i号梁产生的竖向反力；ηi4为单位竖向荷载作用在4号梁对i号梁产生的竖向反力。

第i号梁扭矩分配系数：

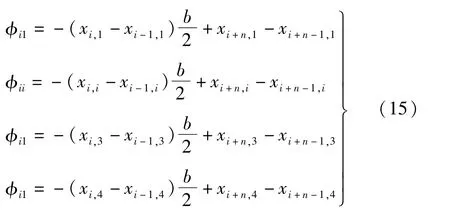
式中：φi1为单位竖向荷载作用在1号梁对i号梁产生的扭矩；φii为单位竖向荷载作用在i号梁对i号梁产生的扭矩；φi3为单位竖向荷载作用在3号梁对i号梁产生的扭矩；φi4为单位竖向荷载作用在4号梁对i号梁产生的扭矩。

根据文献[6]，对计算所得横向分配系数采取线性内插方法计算第i号梁的荷载横向分布影响线。任意位置处的荷载P＝1对i号梁产生的竖向荷载计算如图5所示，至于任意位置处荷载P＝1对i号梁产生的扭矩则只需将相应竖向荷载分配系数η换为扭矩分配系数φ。

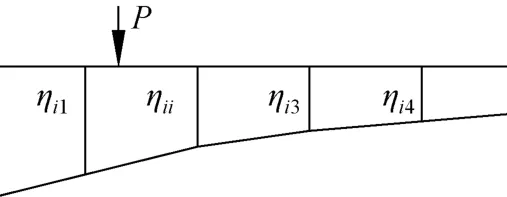
图5 i号梁荷载横向分布影响线计算示意Fig.5 Transverse distribution influence line of beam i

2 参数分析

为了探索出弯梁桥横向分布系数与桥梁跨径L以及曲率半径R的关系，利用MATLAB程序，根据上述相关理论，编写相关程序得到理论计算结果用以分析多梁式钢-混组合弯箱梁桥横向分布与桥梁跨径和曲率半径之间的关系。

计算模型如下：弯箱梁桥的组合箱梁由U型钢梁通过剪力连接件和混凝土顶板连接而成，U型钢梁设有加劲肋和横隔板。主梁组合箱梁桥面宽17.8m，梁高为2.47m，每个U 梁宽2.27m，混凝土板厚220mm，U型钢梁腹板与底板厚20mm，底板纵向加劲肋与腹板横向加劲肋厚也为20mm，横隔板厚16mm。钢材为Q235B，弹性模量为2.06×1011MPa，泊松比为0.3。混凝土标号为C50，弹性模量为3.45×1010MPa，泊松比为0.167。主梁截面如图6所示。

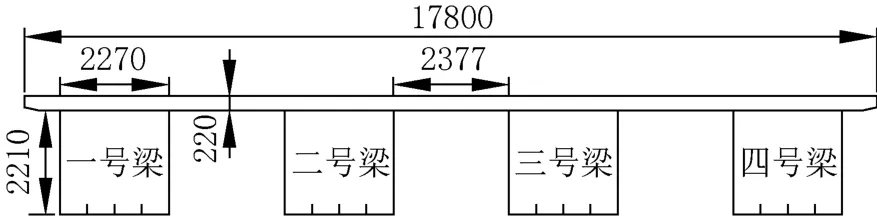
图6 箱梁横截面示意Fig.6 Cross section of box girder

由于截面不变，故参数L只从20m～50m变化，以5m每级递增；参数R从50m～300m变化，以50m每级递增。结合曲线梁桥外侧主梁受力挠度大的特点，本文主要研究一号梁，计算结果如表1～表8所示。

由表1～表8可知：对于中等跨径曲线桥梁，随着跨径的增大，一号主梁竖向荷载横向分布系数逐渐减小，扭矩分布系数绝对值却逐渐增大；随着曲率半径的增大，一号主梁的竖向荷载横向分布系数则逐渐增大，扭矩分布系数绝对值却逐渐减小。

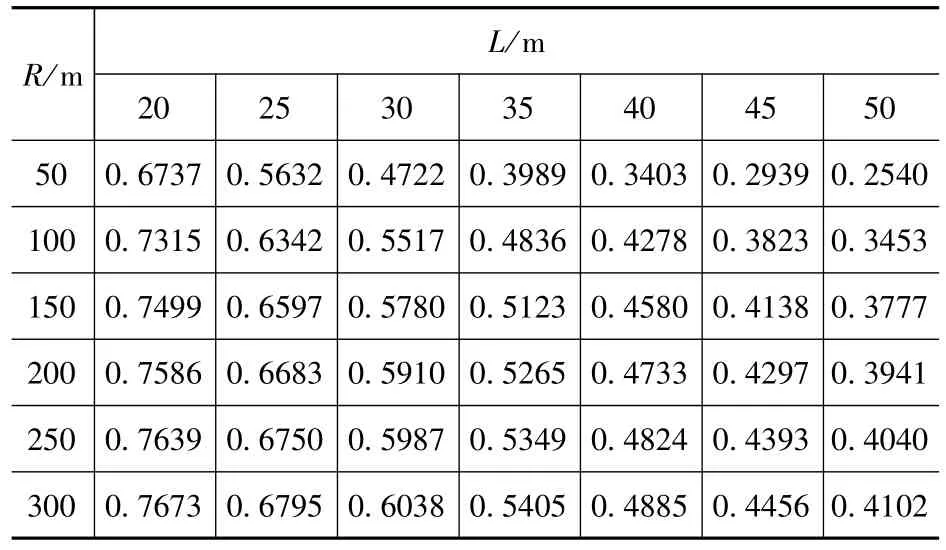
表1 η11Tab.1 η11

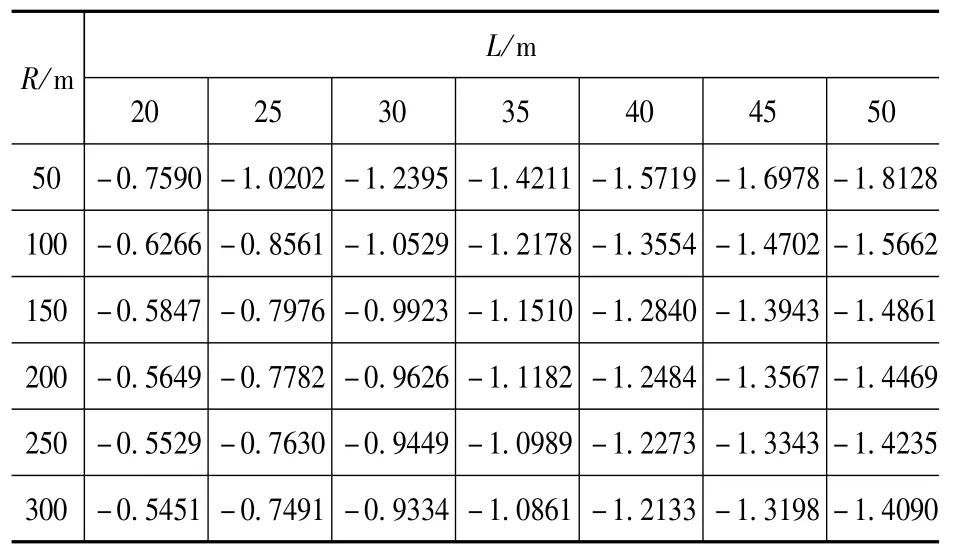
表2 φ11Tab.2 φ11

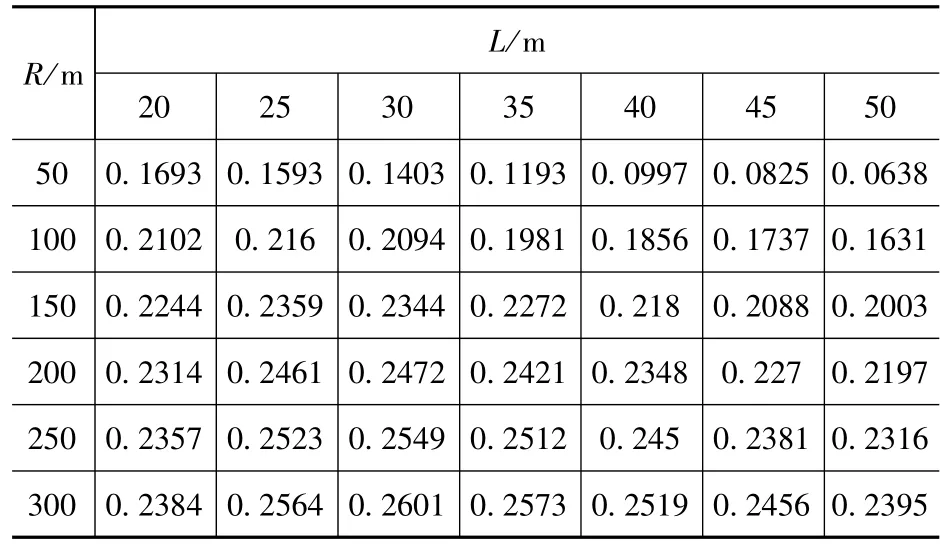
表3 η12Tab.3 η12

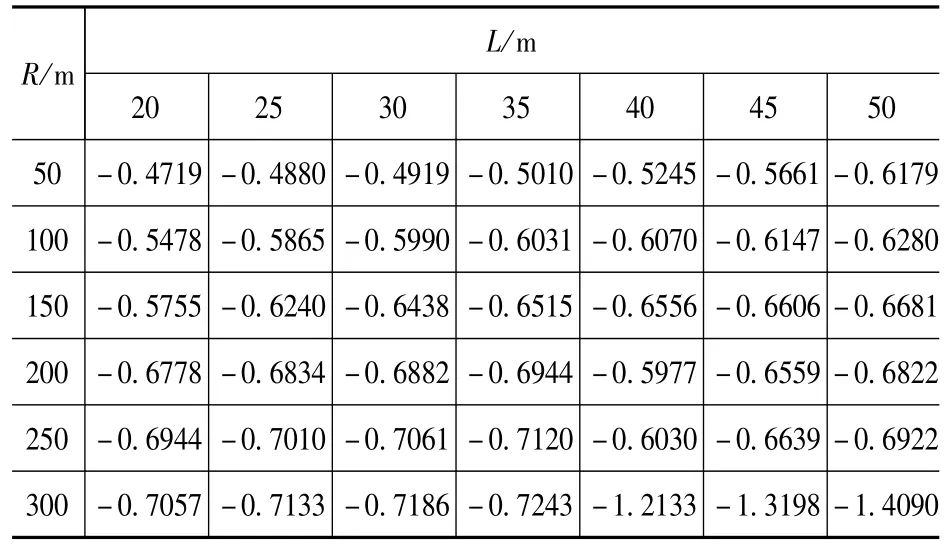
表4 φ12Tab.4 φ12

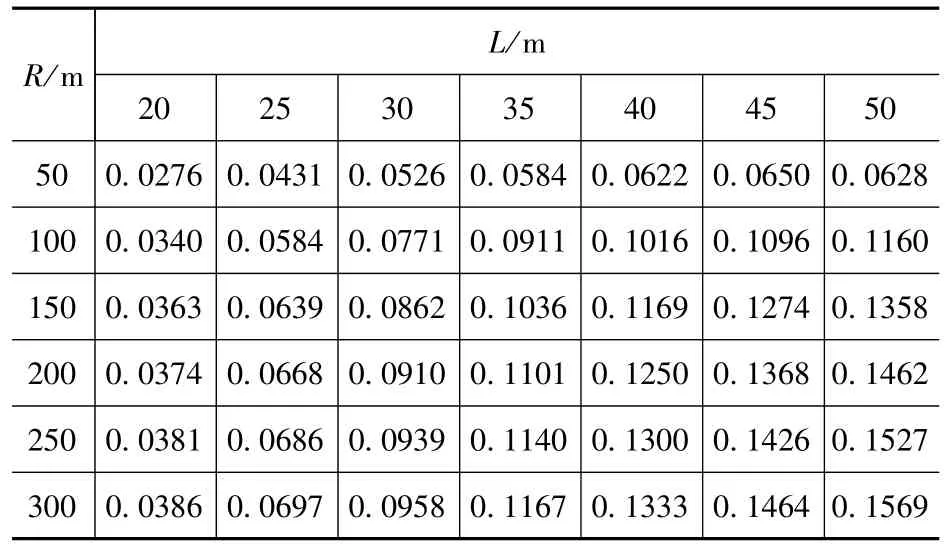
表5 η13Tab.5 η13

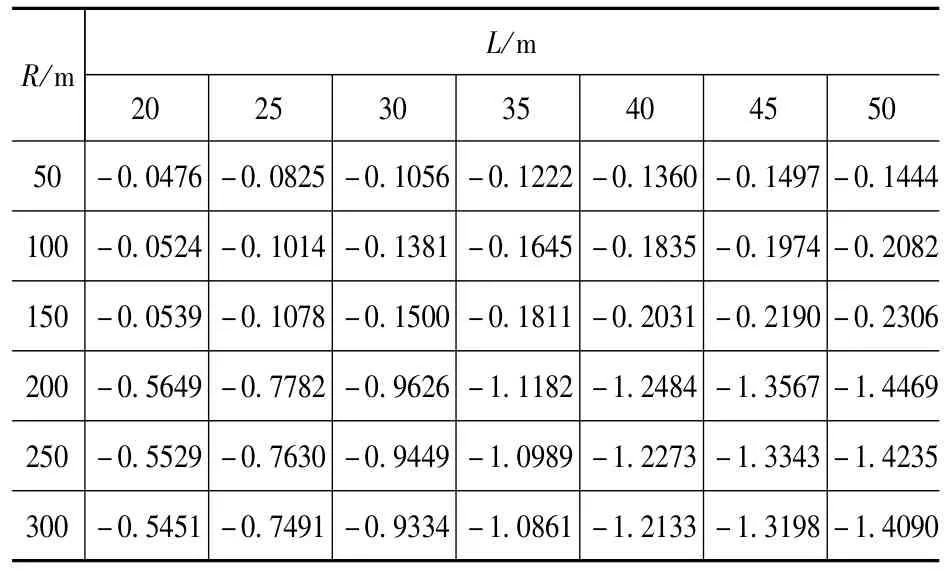
表6 φ13Tab.6 φ13

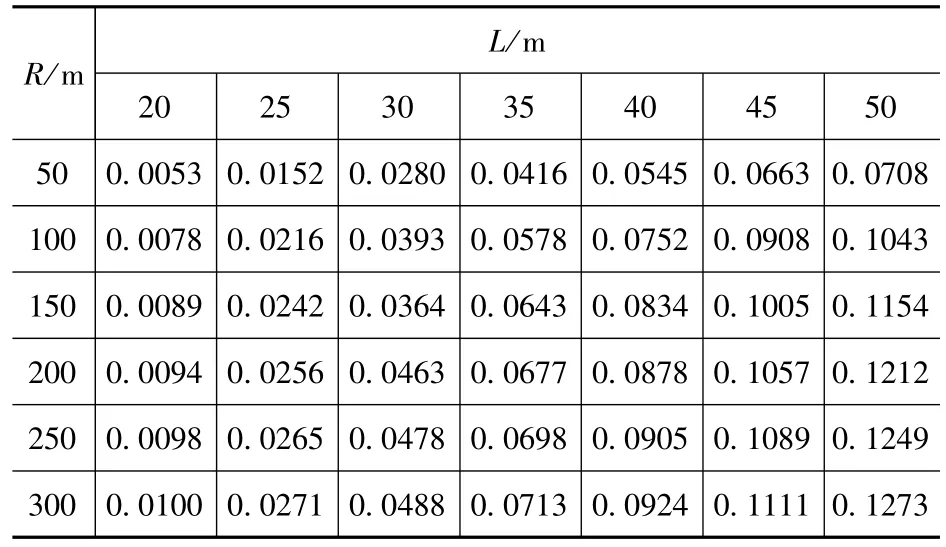
表7 η14Tab.7 η14

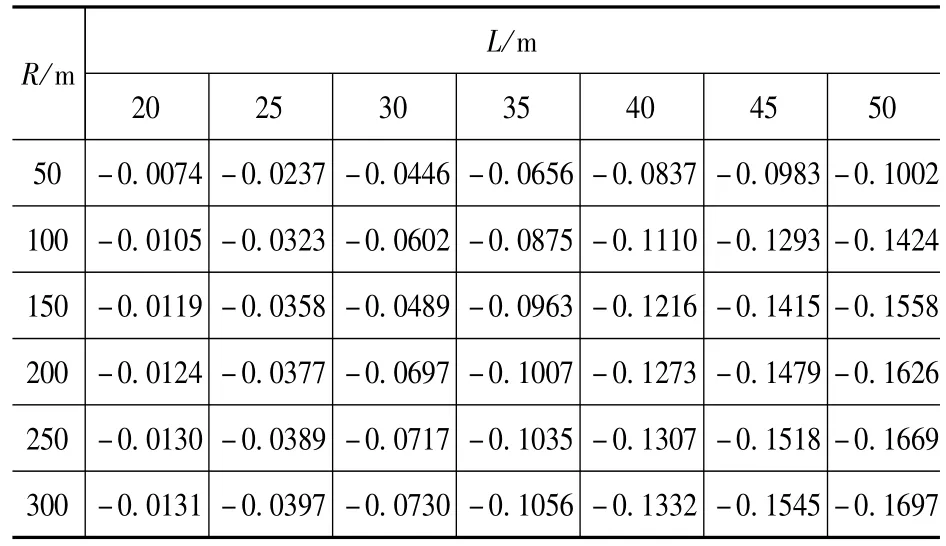
表8 η14Tab.8 η14

为了更直观地反映一号梁横向分布系数随跨径、曲率半径的变化规律，将表中数据画成变化趋势图，如图7～图10所示。由图7～图10可知：对于中等跨径曲线梁桥，当半径不变时，一号梁竖向荷载横向分布系数曲线和扭矩横向分布系数曲线变化趋势与线性变化十分接近；当跨径不变时，一号梁竖向荷载横向分布系数曲线和扭矩横向分布曲线斜率均减小，变化趋势均类似于指数变化。

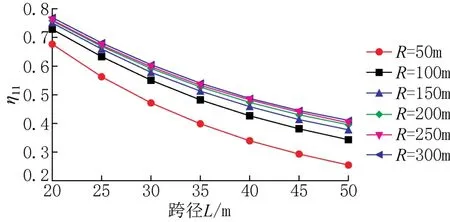
图7 η11随跨径变化Fig.7 Variation of η11with span

3 有限元对比分析

根据上述计算模型，采用大型通用有限元程序ANSYS建立三维空间模型进行计算分析。其中混凝土顶板采用SOLID65单元模拟，U型钢梁采用SHELL63单元模拟。一共建立12个有限元模型用以用来和理论计算结果进行比较分析，模型如图11所示。12个模型为跨径L从20m～50m变化，以10m递增；半径R从100m～300m变化，以100m递增。

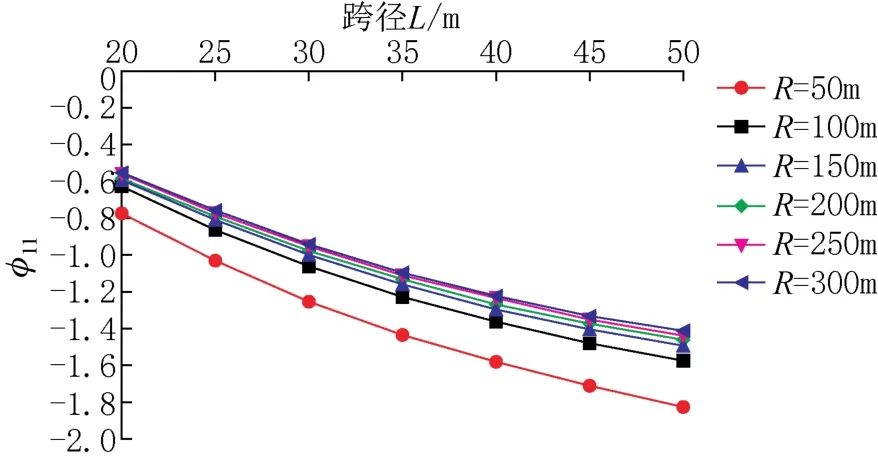
图8 φ11随跨径变化Fig.8 Variation of φ11with span

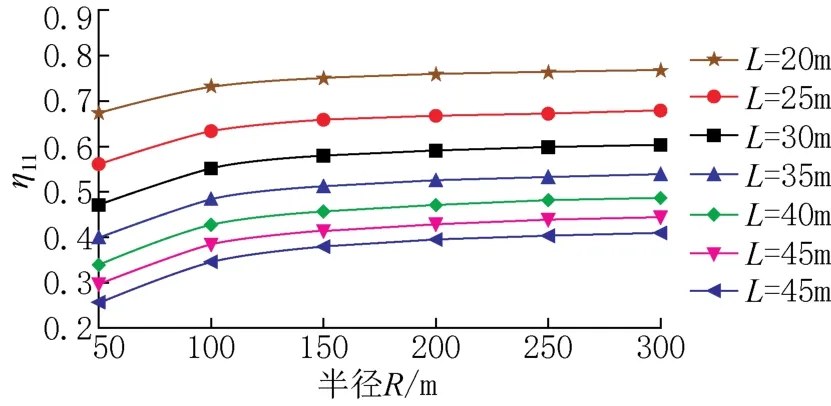
图9 η11随半径变化Fig.9 Variation of η11with radius

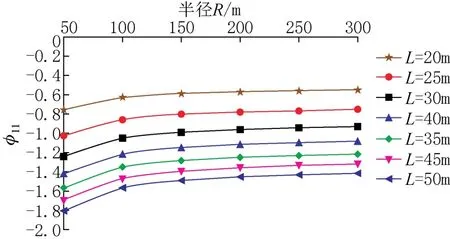
图10 φ11随半径变化Fig.10 Variation of φ11with radius

根据前述单梁挠度计算公式，以R＝100m，L＝30m、40m、50m 为例分别计算在F＝140kN作用在一号梁跨中时，一号梁的跨中挠度（见表9）。其他曲率半径和跨径下的挠度计算同理。

图11 有限元模型Fig.11 Finite element model

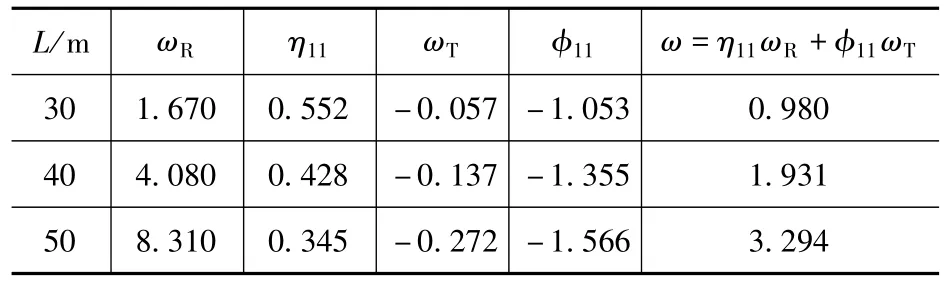
表9 R＝100m挠度理论计算结果Tab.9 Deflection of R ＝100m

表10 理论与有限元计算结果对比Tab.10 Results of theory and finite element method

根据表10可得：当跨径较小和曲率半径较大时，理论计算结果与有限元计算结果误差稍大，但大多都在5%～8%内变化且均不超过10%，对于其他情况则结果误差很小，甚至能达到小于2%。说明刚接梁法适用于计算多梁式钢-混组合桥梁而且计算精度是足够的，用该方法计算总结所得规律也是正确的。

4 结语

本文针对多梁式钢-混组合中等跨径弯箱梁桥的横向分布计算问题，结合曲线桥受力特点，通过改变跨径和曲率半径等参数利用MATLAB程序进行理论计算，得出各主梁的横向分布系数并分析总结相关变化规律，然后与ANSYS有限元计算结果对比分析检验结果的正确性。文中只列出一号梁的数据，但是由计算结果发现各梁规律是类似的，且弯桥外侧梁受力大、挠度大，故选择一号梁进行分析。最终得出如下结论：

1.刚接梁法不仅适用于钢-混组合直桥以及混凝土弯桥的横向分布，对钢-混组合弯桥也同样适用，而且计算结果精度相当高，对工程实践具有一定的参考意义。

2.对于中等跨径曲线桥梁，随着跨径的增大，主梁竖向荷载横向分布系数逐渐减小，扭矩分布系数绝对值却逐渐增大；随着曲率半径的增大，主梁的竖向荷载横向分布系数则逐渐增大，扭矩分布系数绝对值却逐渐减小。

3.对于中等跨径曲线梁桥，当半径不变时，主梁竖向荷载横向分布系数曲线和扭矩横向分布系数曲线变化趋势与线性变化十分接近；当跨径不变时，主梁竖向荷载横向分布系数曲线和扭矩横向分布曲线斜率均减小，变化趋势均类似于指数变化。