基于模态分析及动刚度优化的低噪声正时罩设计
李林洁,毕嵘,张良良,韦静思,占文锋
(广州汽车集团有限公司汽车工程研究院,广东广州 511434)
0 引言
近年来,随着汽车工业发展日趋成熟,人们对汽车的要求也日益提高。除了动力性以外,舒适性也成为汽车评价的重要指标。汽车噪声作为舒适性的一个重要指标开始受到越来越多的关注[1-3],因此,发动机的振动噪声控制成为发动机结构设计领域的又一热点。
正时罩盖属于薄壁件,刚度小,面积大,很容易与跟它相连的发动机体发生共振,辐射噪声较大。正时罩盖的辐射噪声是发动机辐射噪声的主要来源之一,占发动机整体噪声的比例较大,通常发动机前端的噪声要比其他表面的噪声高3 dB[4]左右。因此,有效降低正时罩盖的辐射噪声成为正时罩盖优化设计的重要目标。
近些年来,大批专家学者对正时罩盖的减振降噪进行了研究。文献[4-5]中分别通过拓扑优化及形状优化对某型号内燃机的正时罩盖进行了优化设计,利用拓扑优化对内部生成加强筋的材料进行了重新布置,取得了满意的效果。卢兆刚等[6]利用频谱分析和模态分析获得正时罩辐射噪声的关键模态,然后利用拓扑优化的方法对其内部的加强筋进行了结构优化。
本文作者利用有限元的方法分析装配状态下正时罩盖的各阶振型,获得其噪声辐射的关键模态;并施加单位载荷于正时罩盖的有限元模型,将其作为动态响应分析的激励,得到正时罩盖表面响应分布,然后通过试验来验证其模型准确性。文中以动刚度作为优化目标,对其内部的加强筋进行了重新设计及布置,使该正时罩盖的模态振型避开正时轮系啮合激励频段, 进而降低辐射噪声,仿真和试验结果验证该方法的有效性。
1 动刚度理论
动刚度是指在交变载荷作用下抵抗动态变形的能力。它可以表示为产生单位振幅所需要的动态力,是衡量结构抗振能力的常用指标。在动态力作用下,结构动刚度越大,振动量越小;反之,结构动刚度越小,振动量越大。对于一个确定的系统,动刚度为频率的函数,其数值取决于结构本身的参数:静刚度、阻尼和质量。
根据物理定律有公式(1)—(3),可推导动刚度公式K:
(1)
ω=2πf
(2)
K=F(ω)/X(ω)
(3)
式中:a为相应点随频率变化的加速度,m/s2;X(ω)为相应点随频率变化的位移,m;F(ω)为激励点随频率变化的载荷,N;ω为圆频率,rad/s;f为固有频率,Hz;K为相应点随频率变化的刚度,N/m。
加速度导纳为加速度与激励力的比值,如果振动加速度的响应点和激励点重合,其比值称为源点加速度导纳,函数表达式如式(4):
(4)
式中:aIPIf为源点加速度导纳响应(IPI)分析所得曲线上对应的纵坐标加速度值。
当频率f=fi(i>0)时,由式(4)得到频率fi时的动刚度为
(5)
如果通过IPI分析得到图1中的响应曲线(对数曲线),根据式(5)可以得到图2中的动刚度曲线K(对数曲线),纵坐标为每个频率fi对应的动刚度值Kfi。

图1 IPI响应加速度曲线

图2 IPI响应刚度曲线
便于对结果处理,一般直接采用IPI响应曲线进行分析,并采用分析点的等效动刚度Ka与动刚度目标值Kd比较,从而对动刚度特性进行分析。
由IPI分析得到的响应曲线,如图1所示,计算曲线所包围的面积,则有公式(6):
(6)
式中:sIPI_K为IPI分析中IPI_K曲线所包围的面积;Δf为计算频率步长。
令
(7)
将式(7)代入式(6)得到该连续点的等效动刚度Ka,见公式(8):
(8)
由式(4)可作出目标动刚度Kd的IPI响应曲线IPI_Kd,如图1所示。
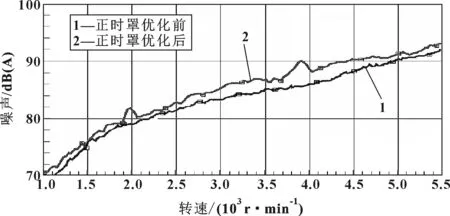
如果图1中的曲线IPI_K所包围的面积小于目标曲线IPI_Kd所包围的面积,则表示该连续点的等效动刚度Ka≥Kd;如果图中曲线IPI_K在某频率下在IPI_Kd下方,则表示该连续点在该方向该频率fi的动刚度Kfi≥Kd(i>0);反之,Kfi 通过有限元的方法实现动刚度数值仿真计算,模型是否正确关系到仿真结果正确与否的最为基础的环节。将有限元模型用于仿真计算前,需要对其有效性进行验证计算,即需要进行模态分析。为了保障模型边界条件的准确性,有限元模型包含油底壳、缸体、缸盖、缸盖罩、凸轮轴、正时罩盖、进气歧管、右悬置支架等,采用二阶四面体网格对各零部件进行有限元建模,忽略机体的铸造圆角与螺栓孔倒角,如图3所示。 图3 有限元模型 在实际工作过程中,正时罩盖是和机体、缸盖通过螺栓连接在一起的,建立零部件的连接关系时,在HyperMesh中通过bar单元实现螺栓连接,其他螺栓连接部位也采用bar单元的连接方式,电机、空气压缩机、节气门等附件系统以质量点代替,附加转动惯量,并通过REB2的形式与周围的网格连接。将图3所示的有限元模型,导入ABAQUS软件中进行求解,得到正时罩盖的前4阶模态,如图4所示。 图4 模态分析结果 根据材料参数测试的结果设定有限元模型的材料参数,以模态分析的有限元模型为基础,建立频响分析模型,如图5所示,图中点1001、1002为响应特征节点。 图5 频响分析模型 在整机条件下,对正时罩盖进行频响测试,参考有限元模型中的激励点及响应特征节点,频响结果如图6所示。从图中可以看出,源点1001测试结果与仿真结果相近,且动刚度水平较低,与整机边界下正时罩盖的1阶模态相对应;源点1002动刚度水平较高,且频响峰值与正时罩盖的3个主要模态相对应。 图6 频响分析结果 为了验证正时罩盖结构参数与辐射噪声的关系,在消声实验室中,进行1 m声压级测试,如图7所示。 图7 噪声测试 对发动机正时罩盖进行近场噪声测试时,频率为1 400 Hz频段对噪声的贡献最大,如图8所示。频响峰值频率对应了正时罩盖近场噪声共振频率带中心频率,推测正时罩盖在中心频率1 400 Hz时发生共振。为此,通过提高正时罩盖的动刚度,进而使罩盖的固有模态避开该频率范围,尽可能减少共振的可能性。 一般来说,正时罩盖为大面积薄壁件,且布置了许多安装孔,使得其动刚度较弱,容易引起整体的一阶弯曲振动,整机边界条件下的模态计算也证实了这一点。因此为了提高正时罩盖的动刚度,必须在满足强度要求的前提下,在动刚度薄弱的部位增加加强筋,使得整体的刚度分布更加合理,经过反复修改和计算后,确定有效改进措施,优化后的结构如图9所示。 图9 优化前、后有限元模型 对优化的后正时罩盖进行动刚度计算,并通过试验来验证优化结果,如图10所示。优化后的部位动刚度有显著的提高,基本达到目标值要求。 图10 优化前、后动刚度对比 图11为台架噪声试验测试结果,测试点为靠近发动机正时罩盖侧。通过正时罩盖优化前、后声压对比可以看出:在整个转速工况范围内,优化后的辐射噪声有了明显减小;同时,转速为2 000 r/min与3 800 r/min工况下出现的峰值也消失。通过优化刚度,实现了降低辐射噪声的要求。 图11 噪声测试结果对比 CAE 技术的迅速发展使得工程师们可以在计算机上预测发动机及整车的NVH性能,还节省了大量的时间和成本。文中正是基于数值仿真技术,以提高发动机机体的固有频率、优化其动刚度分布为目标,对正时罩盖进行了结构优化。通过对正时罩盖薄弱处增加加强筋,避开了正时罩的一阶模态,减小其共振的可能性,同时动刚度得到了很大的提高。试验结果表明,优化后的正时罩盖对改善整机的辐射噪声效果明显。2 有限元计算及实验对比
2.1 模态分析

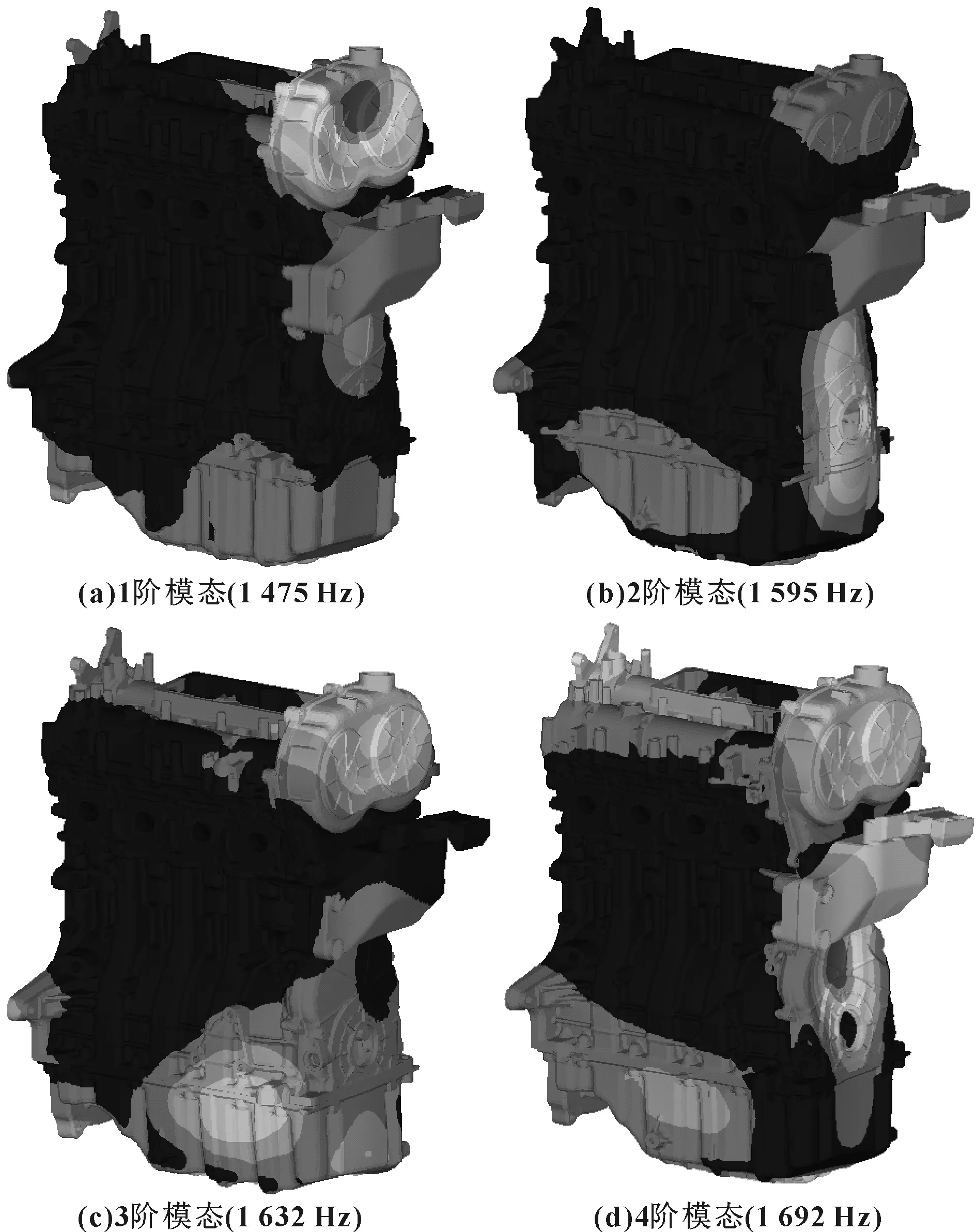
2.2 频响分析





3 结论

