基于智能突现的无人机群自主编队控制研究

叶圣涛，方洋旺，朱圣怡

（空军工程大学航空航天工程学院，西安 710038）

0 引言

无人机自20世纪20年代问世以来，其在战争中的地位日益提高[1]。多无人机协同自主编队飞行是近年来的一个前沿领域，可充分利用单机资源，共同执行复杂任务。因此，针对无人机群自主编队的深入研究具有重大意义。

群体智能（Swarm Intelligence）即群体产生的智能，与集体智慧类似[2]。突现计算（emergence computation，又称涌现计算[3]）是多 agent系统（multi-agent system，MAS其中agent又称个体或智能体）处理复杂问题时所展现出来的一种创新思路逻辑，是通过多个简单模块的相互沟通和协作来突现出更加复杂行为的计算系统。

在传统的多无人机自主编队中，需要无人机之间进行大量的信息交互，算法复杂，计算量大，耗费时间长，不能满足系统的快速性、实时性要求[4]。王品、姚佩阳利用一致性算法求解了线性化无人机模型，并利用Lyapunov理论证明了系统的稳定性[5]。万婧、艾剑良通过模糊控制为无人机编队设计了控制系统[6]。本文提出了一种基于智能突现分布式控制策略来解决无人机群自主编队控制的问题，为单个无人机设计简单的运动规则，通过多个无人机的相互通信和影响来突现以形成编队队形[8]。

本文针对鸟群飞行机制中的Leader-Follower态势进行建模：一方面利用有向图描述无人机之间的通信协议；另一方面遵循聚类，防撞和速度一致三项规则[9]为无人机设计简单的飞行控制器，通过多个无人机间的相互通信和协作以达到智能突现下的自主编队。

1 无人机群自主编队控制方法

1.1 基于Swarm模型的无人机编队建模

考虑n维空间中具有个数分别为M个领航者，N个跟随者组成的Swarm集合，用表示，其中为第i个领航者的位置，为第j个跟随者的位置向量；为控制参数集；，为第i个领航者的速度向量，为第j个跟随者的速度向量；，为第i个领航者的加速度向量，为第j个跟随者的加速度向量。领航者和跟随者的运动由以下方程控制：

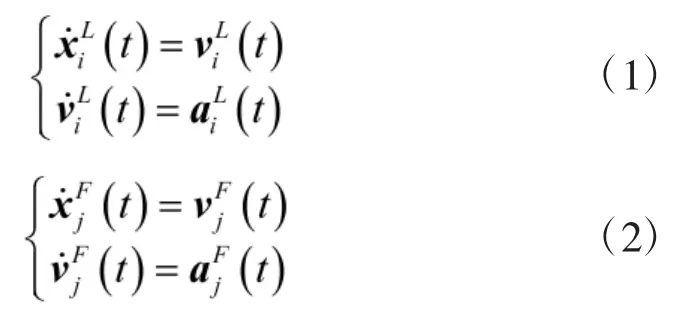
对于每一个领航者，其根据目标位置，采用比例导引法[10]命中目标。可得到位于水平面和垂直面的加速度和分别为

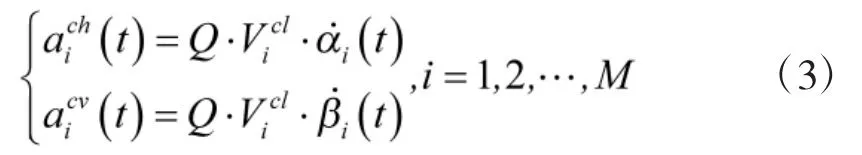
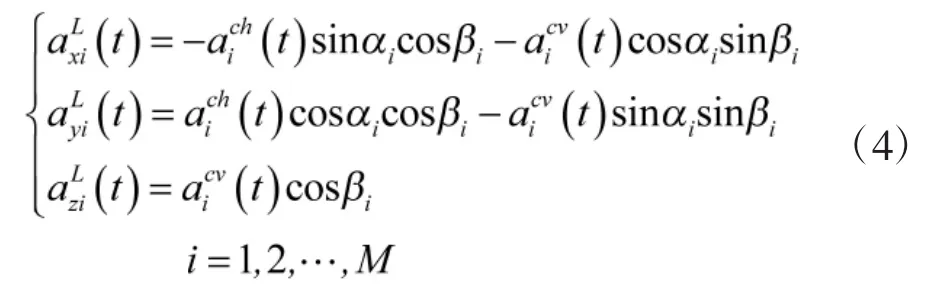
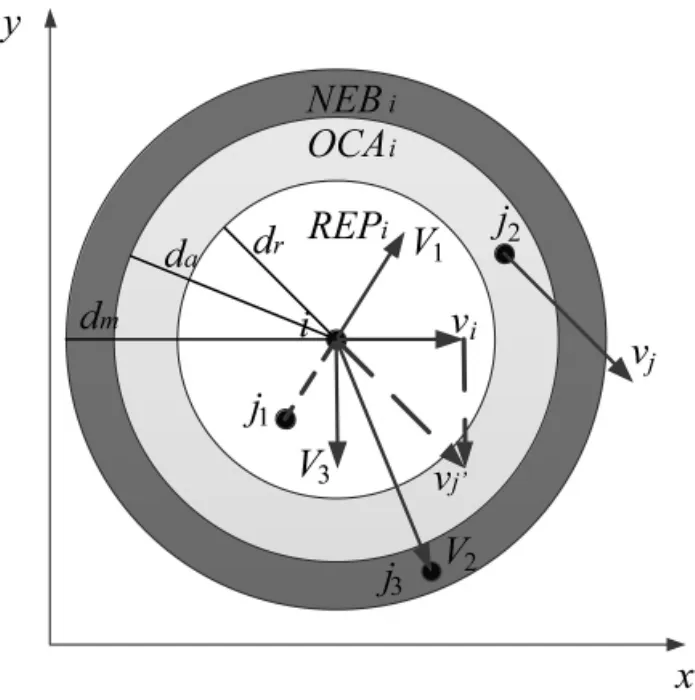
图1 平面内无人机间影响作用图

如图1所示，定义第i个跟随者的排斥域、吸引域和速度修正域[7]分别为

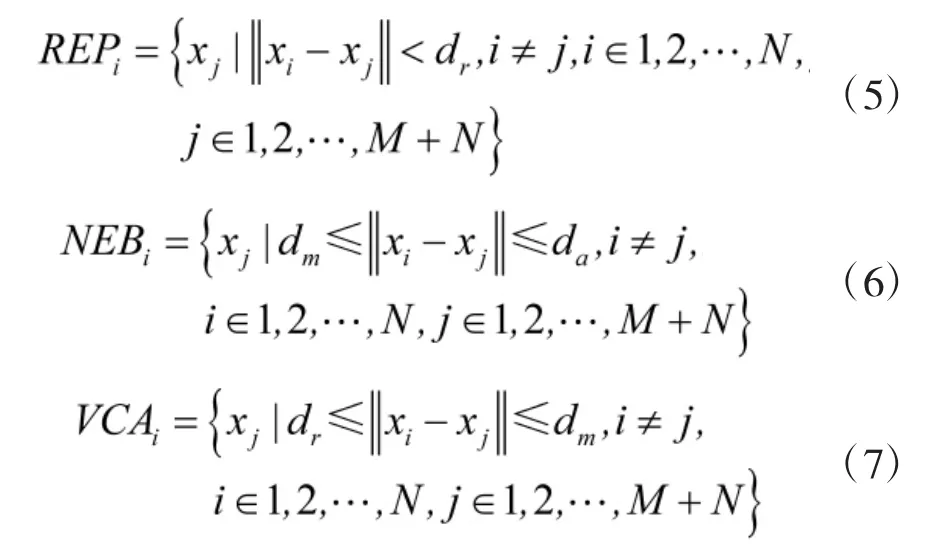
定义第i个跟随者的排斥向量，吸引向量，速度修正向量[4]分别为：

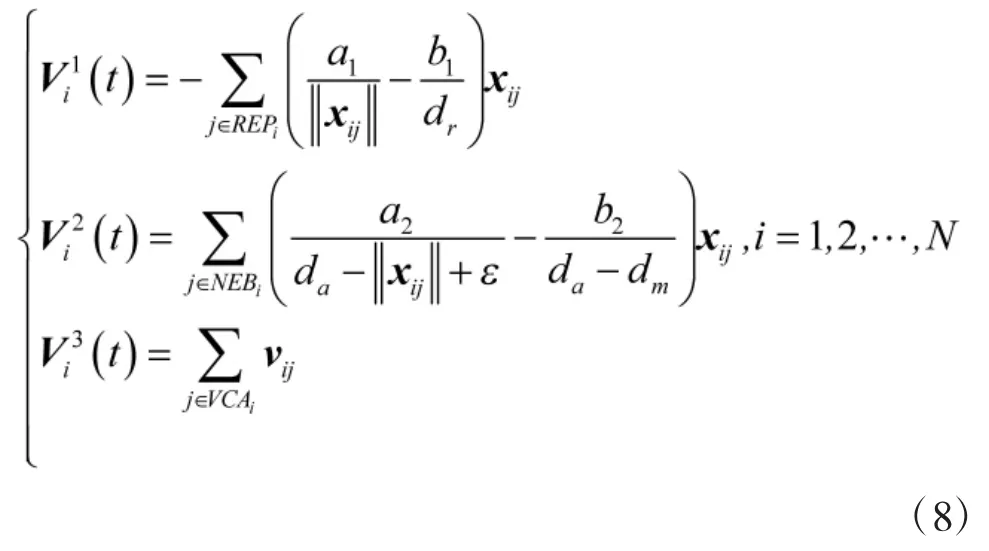
定义每个跟随者的加速度为

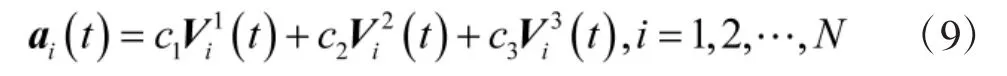
式中：ci（i=1，2，3）为增益系数，根据系统的规模和要求而调整。

假设每个无人机的加速度值及速度值由以下条件约束：

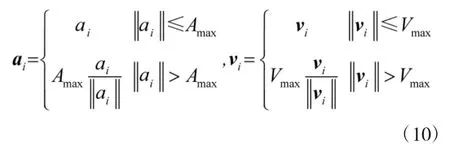
1.2 无人机运动建模

下面将建立三自由度的无人机运动学模型，由于每个无人机的模型（包括领航者和跟随者）都是相同的，故去掉上下标。方程如下：

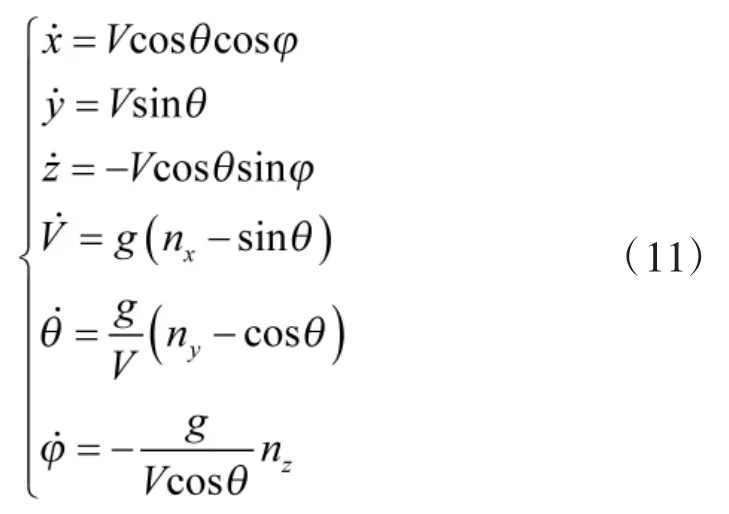
其中，（x，y，z）表示无人机在惯性坐标系中的位置；V，θ，φ分别表示无人机的速度、弹道倾角和弹道偏角；nx，ny和nz分别为无人机过载矢量在弹道坐标系各轴上的分量。

1.3 无人机制导控制方法

对于无人机群中的每一个领航者，假设其上安装有高性能导引系统和定位系统，可以准确地发现目标，并且能够实时测得目标位置及自身位置，从而测得自身到目标的视线角速度，进而通过比例导引律控制领航者的制导与飞行来攻击目标。其制导与控制方法详见参考文献[10]。这里直接给出领航者的过载信息为：

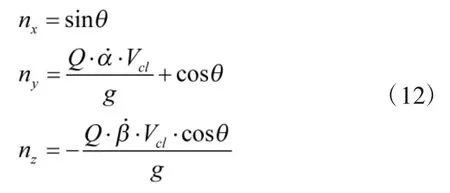
式中：Q为比例导引系数，一般取3到5之间；α，β分别为每一个领航者飞行过程中与各自目标的视线倾角和视线偏角；Vcl为每一个领航者与各自目标的相对接近速度。

为了简化模型，这里取 nx=sinθ，使得式（11）中的，则Vj（t）为一定值，即每一个领航者以恒定速度飞向目标。

对于无人机群中的每一个跟随者，假设无人机协同数据链能够准确传输信息且无延迟，跟随者能够通过无人机协同数据链获得周围无人机的状态信息。无人机间的通信方式用有向图G=（V，E，A）表示无人机间的通信拓扑关系，如图2。其中V={v1，v2，…，vn}为图的节点集，每架无人机对应一个节点；E为图的边集，边表示第i架无人机可以单向获取第j架无人机的位置和速度信息；A=为有向图的邻接矩阵，当i=j时，aij=0，i≠j时，若 eij∈E，aij=1，否则 aij=0。

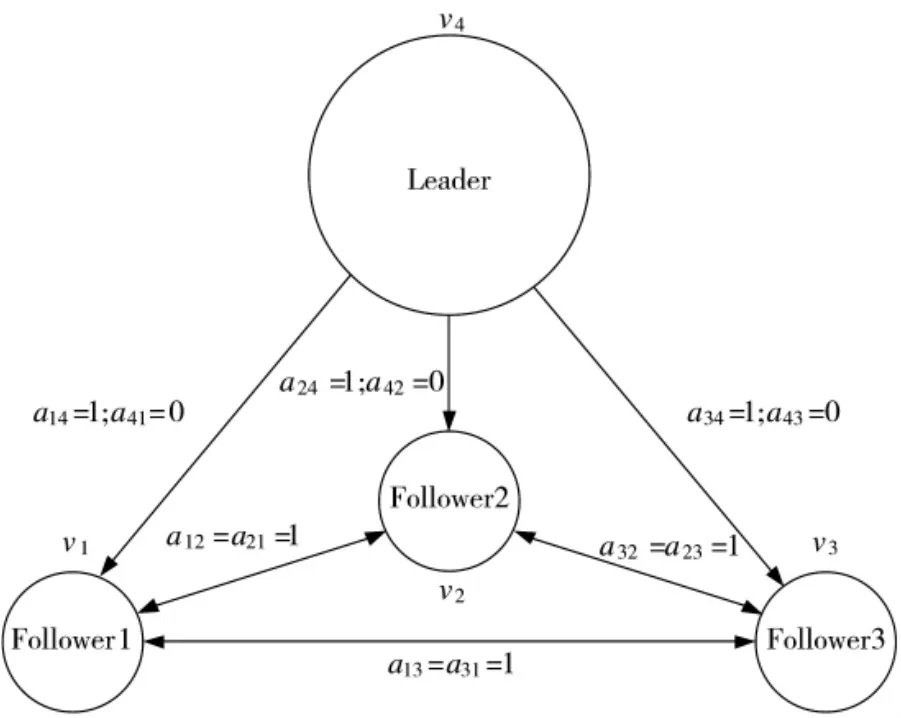
图2 无人机群有向通信示意图

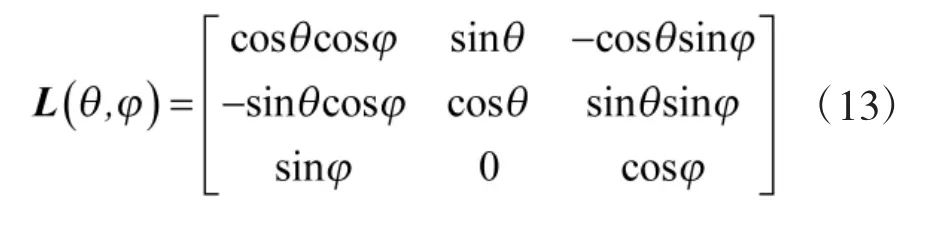
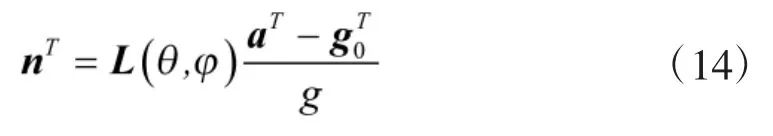
将得到过载矢量nT代入式（11），从而解得每一个跟随无人机的位置信息。

2 仿真分析

考虑如下情景：在战场空间中，存在敌方地面固定目标6个，我方由运输机在高空均匀投放无人机若干架，其中包括具有高性能导引头的领航无人机和普通跟随无人机，仿真时间为40 s，步长为0.1 s。

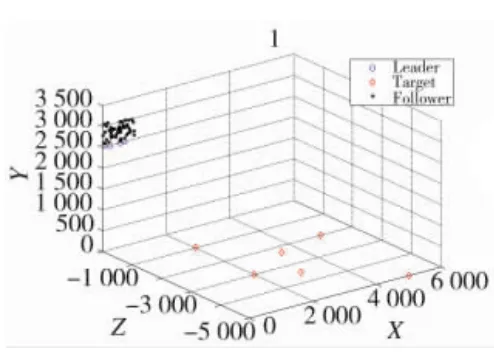
图3 仿真初始时刻图

图4 队形散开避免碰撞图

如图3所示，仿真初始化，地面上有6个敌方固定目标，用红色菱形表示，我方运输机在高空随机投放56架无人机，其中6架为带有高性能导引头及定位系统的领航无人机，其任务为探测敌方目标并实现制导，带领着普通跟随无人机攻击目标，在仿真图中以蓝色圆圈表示；其余50架为普通跟随无人机，其任务为跟踪上领航无人机，保持集群飞行，毁伤地面目标，仿真图中以黑色圆点表示。

如图4，编队初期，由于跟随者和领航者之间的位置都是随机，并且跟随者之间的速度也不尽相同，无人机群整体呈现较混乱的态势，如图4所示的两架跟随无人机（黑色箭头所指）由于初始位置距离整体中心太远，速度方向向外，因此，有远离整体中心移动的趋势。其他跟随无人机迅速通过数据链获取通信范围内其他无人机的速度和位置信息，由于初始投放距离短，使得无人机之间的距离都过于靠近，为了避免发生碰撞，无人机在受到排斥作用下开始有序散开，并开始逐渐编队。

如图5所示，一些在初始状态下远离整体的跟随无人机，随着距离的逐渐增大，吸引作用逐渐增强，排斥作用逐渐减弱，均有飞回无人机群整体的趋势（图5黑色箭头所示）。

如图6所示，随着飞行的继续，仍旧有跟随者（图6黑色箭头所指）因为吸引作用不足而导致飞出了通信范围，进而失去了无人机群的控制，从而运动呈现不规则性。

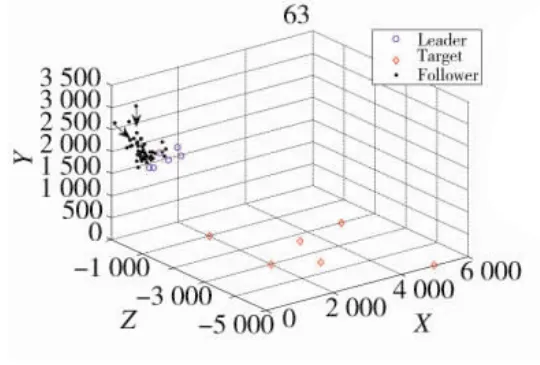
图5 跟随无人机飞回无人机群

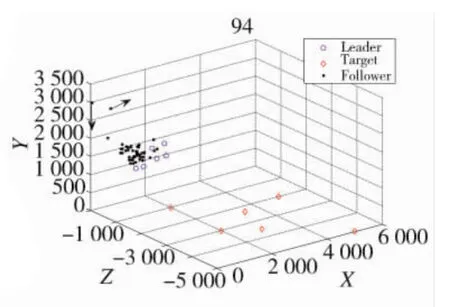
图6 跟随无人机飞出通信范围失去控制

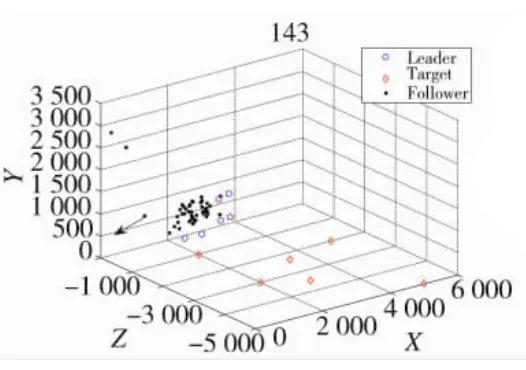
图7 跟随无人机飞出通信范围失去控制

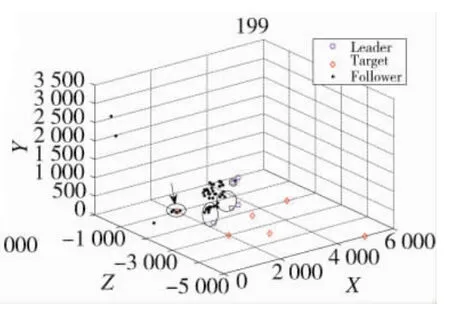
图8 领航者1带领跟随无人机毁伤目标1

图7中，在无人机群中，随着各个领航者飞向各自的目标，跟随者中突现出分群的现象，图7中的无人机群已经开始逐渐形成Leader-Follower的初期态势，由领航无人机带领若干跟随无人机飞向各自目标。不过仍然存在无人机（图7黑色箭头所指）飞出通信范围而飞离无人机群的控制范围。

图8为仿真20 s左右，无人机群编队飞行已经基本稳定，已经明显出现Leader-Follower态势。领航者1已经带领4个跟随者到达了目标附近，剩下的跟随者继续跟随着剩下的领航者飞向目标，并且明显形成编队飞行（图8黑色圆圈所示）。

图9 领航无人机2，4带领跟随无人机毁伤目标2，4

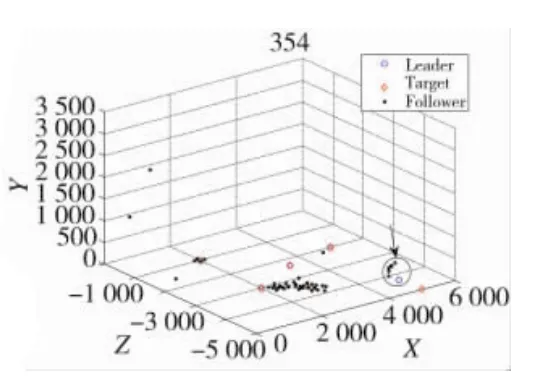
图10 领航无人机6带领跟随无人机群飞向目标6

图9中而由于目标2和目标4相对距离靠近，领航者2和领航者4共同带领着一大群跟随无人机（黑色椭圆圈所示）攻击各自的目标。领航者5只带领了一个跟随无人机攻击到目标5。

图10中最终由第6个领航者带领着剩下的跟随无人机飞向目标（图10黑色箭头圆圈所指示）。

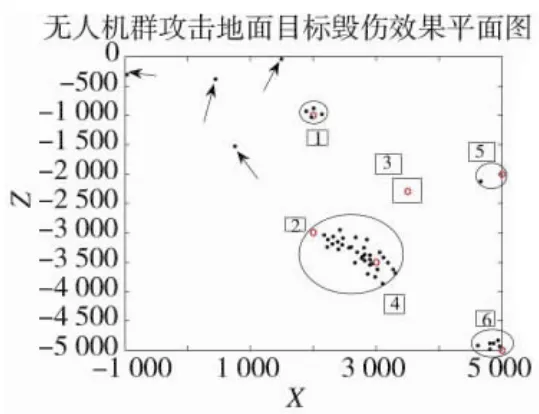
图11 仿真结束时毁伤目标效果平面图

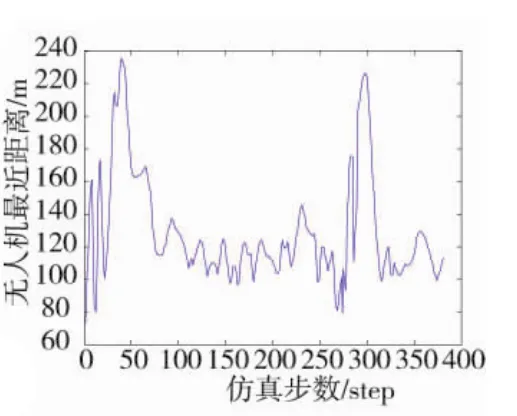
图12 飞行过程中无人机间最近距离图

下页图11为仿真结束时，所有个体在水平面的散落情况，可以清楚地看出，有4架跟随者由于初始状态或者飞出了通信范围而不受控制（黑色箭头所指），从而远离了无人机群的整体，无序地散落在水平面内。剩下的跟随者由6架领航者带领分别飞向各自的目标，其中领航者2和领航者4由于目标位置相对接近，因此，共同带领着一大批跟随无人机攻击目标2和4，领航者1、5和6都带领着各自的跟随者攻击目标，领航者1和6所带领的无人机群几乎均匀地散布在目标周围，毁伤效果优良；领航者5所带领的跟随者较少，毁伤效果一般。其中第3架领航者（黑色方框所圈）由于失去了对跟随者的控制，没有跟随者跟随，独自攻击目标。

图12为无人机群飞行过程中，每一时刻无人机群中无人机之间距离最小值的变化曲线，由图像可知，无人机之间的距离保持相对稳定，从而确保了无人机之间不会发生碰撞。

由上述仿真结果可以看出，利用本文提出的群体智能算法及分布式通信策略，当无人机飞行一段时间以后就产生突现现象，形成攻击编队对目标进行了有效攻击，从而验证了本文所提方法的有效性。

3 结论

本文对无人机群的自主编队控制问题进行了研究，为了克服传统无人机群编队中交互信息量大，算法复杂的问题，提出了一种基于智能突现下的分布式无人机群编队控制策略，能够使无人机群中混乱的初始条件下[13]形成稳定的多Leader-Follower编队形式，能够准确地攻击到指定目标并大大增加毁伤范围，为未来战争提供一种新思路。本文研究的数据链之间的通信情况均为理想状态，并未考虑延迟、丢包和噪声的影响。在实际情况中，这些干扰都是不可避免的。因此，研究无人机群在存在各种干扰的分布式通信情况下的自主编队控制问题对未来作战具有重大意义，也是下一步的研究重点。