深水导管架运输分析的荷载与边界优化方法

曾凡权，唐文勇，闫会宾

（上海交通大学 海洋工程国家重点实验室，上海 200240）

0 引 言

导管架因具有结构简单、经济性好和安全可靠等优点而在海洋石油开发、海上风电及海上其他资源开发方面得到广泛应用，并将在未来的海洋资源开发中继续发挥重要作用。

一个优秀的导管架设计方案应考虑结构在建造、安装和使用过程中可能遇到的各种工况，并以此为基础对结构进行优化。运输分析是Pre-service分析中的重要一环，特别是随着导管架日益大型化，运输分析在整体设计中的作用不断提高。在目前的导管架运输分析中，船体运动荷载的预报多采用规范[1]推荐的方法，即直接给出横摇和纵摇等运动的幅度及相应的周期（有关该方法的应用实例可参考文献[2]）。该方法 虽然简单，但并未考虑项目的差异性，导致推荐荷载值比实际值偏大很多，从而使得结构计算结果过于保守。因此，工程中为降低成本，往往需根据实际情况对船体运动载荷进行预报，由此需用更简单合理的处理方法。

目前，已有部分学者对上述问题进行研究。蔡元浪等[3]对深水导管架的运输方法进行总体概括；沈华[4]对货物在运输过程中受到的惯性力进行研究；王冬姣[5]对海洋平台在运输过程中遇到的最大惯性力进行探讨；梁学先等[6]对MOSES软件在导管架安装分析中的应用进行介绍；孙玉柱等[7]对Ansys在上部组块运输中的运用进行研究；柴佳春等[8]对半潜船运输钻井平台可行性方法进行探讨。本文以此为基础，结合工程经验和实际工程算例，对导管架运输分析的基本原理、基本流程和在结构仿真过程中遇到的问题进行探讨，提出一种较为高效的载荷处理方法，并对该方法进行验证。同时，根据实际情况确定边界条件，使考虑的问题更加全面。此外，整理出一份完整的海洋平台运输分析流程，供相关人员参考。

1 运输分析的基本原理

达朗贝尔原理是运输分析的基础，用于将动力学问题转化为静力学问题，也称动静法[9]。

在工程实际中，为简化计算，通常将导管架和驳船看成一个刚体，该系统有6个自由度（横荡、纵荡、垂荡、横摇、纵摇和艏摇），各自由度之间相互独立，即共有3个沿坐标轴的线加速度及3个绕坐标轴的角加速度。根据刚体的平面运动定理[9]，只要采用动静法计算出1个点的运动参数，即可根据该点求出整个结构的惯性力，这就是运输的基本原理。该点称为运动中心，在工程实际中通常将结构物的重心作为旋转中心。

2 计算方法和计算流程

结构计算的准确性主要取决于结构物本身模拟的相似度、外力模拟的合理性和边界条件的处理等3个要素。三者缺一不可。目前拖航分析有以下2种方法：

1) 规范推荐采用的给定横摇/纵摇角和与之相应的周期及垂荡加速度，通过正负组合得到不同的工况；

2) 用水动力分析软件计算出船舶的运动特性并将这些特性作为结构设计的基础参数。

在第1种方法中，规范给的运动强度往往较大，计算出的结果偏保守，因此在详细的运输方案设计中多采用第2种方法，即本文推荐的方法。

2.1 MOSES和SACS

MOSES和SACS是海洋工程中普遍采用的有限元计算软件，其中：MOSES软件主要用于水动力分析；SACS软件集成有多个规范，主要用于处理导管架等桁架结构的有关问题。目前的普遍做法是采用MOSES软件进行水动力分析，将水动力分析结果运用到SACS软件中进行结构强度或其他响应分析，比较常见的有下水分析、运输分析和坐底稳性等，这种方法充分利用2种软件的优点，使计算结果更加可靠。

2.2 结构的模拟

建立的模型要尽量准确，下水支架、滑道及两者之间的木材要根据实际尺寸进行模拟，以保证紧固件受力大小和方向的准确性。原则上，在运输过程中所有结构都要模拟，但在实际操作中可略去一些对结构强度影响不大和质量较小的结构（如“J型管”及其支撑、小的排水管和牺牲阳极等），这样处理不仅能使模型变得简洁，而且不会对分析结果产生较大影响。

此外，紧固件沿船长方向必须布置在驳船的强肋位上，该方式是最高效的传力路径，同时对驳船的甲板有保护作用，因此在设计中应根据驳船的情况合理布置紧固件。

2.3 外力的模拟

2.3.1 重力

对于重力的模拟，除了结构重力以外，还需注意结构重量，可通过在相应位置加质量点的方式模拟。

2.3.2 惯性力的模拟和简化方法

在运输过程中，有 2种力对结构的影响最大，即：运动的惯性力和“重力分量”，后者为倾斜导致的重力沿平行于甲板方向的分量（“G-sin效应”，以下简称“重力分量”）。在实际操作中，可将倾斜时的重力分解为正浮时的重力和重力分量2部分（见图1）。正浮状态单独计算，重力分量与惯性力组合成总的惯性力，最后将两者组合得到总的受力。这样处理可统一模型，方便计算。

图1 重力分量的处理

根据蔡元浪等[3]的观点，切片理论能较好地反映单体船在低速运行时的水动力特性。MOSES软件能运用切片理论，采用频域分析手段预测驳船的运动特性，其做法为：

1) 利用输入的波陡对阻尼线性化或输入基于模型试验得到的阻尼；

2) 计算响应算子（RAO）；

3) RAO与输入的海况组合，获得不同统计概率下的运动响应值。

对于运输分析，一般要考虑 8 个方向的波浪（000°，045°，090°，135°，180°，225°，270°，315°），在每个方向上可得到结构响应的最大线加速度和角加速度，分别为R、P、Y、SW、SU、H（在计算中忽略角速度（即径向加速度）的影响，根据沈华[4]的观点，对于摇荡运动，在横摇或纵摇达到最大角度时，角加速度达到最大，此时离心力为0）。因为6个自由度的运动是相互独立的，若随机进行叠加，同时考虑8个方向，共有512种组合，这在工程上是不能接受的，故应对这些极值的方向进行预判，以减少计算量。图2为波浪方向示意。

假设浪向为090°时船舶具有正向的横荡SW+，此时若角加速度取负值R-，由质心运动定理[9]和质点系动量矩定理[9]可知两者组合时对货物支撑（包括紧固件、下水支架和滑道）的作用力最大，因此该方向下这种组合可认为是极端工况，即在该组合中横摇方向与横荡方向相反（见图3）。纵摇P和纵荡SU也类似，但这2种加速度组合时方向相同，艏摇和升沉运动取所有方向。以此为准，整理出波浪在090°方向和270°时的计算工况见表1。

图 2 波浪方向示意

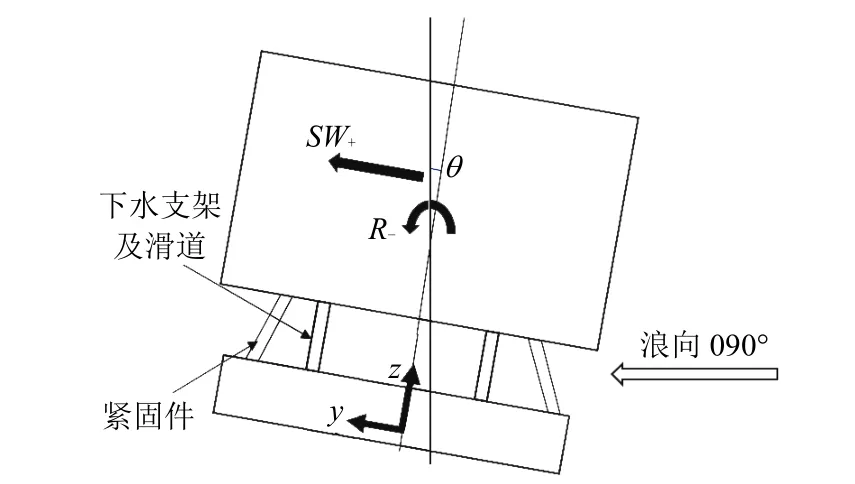
图 3 浪向为 090°时的惯性力组合示意

同理可得其余7个浪向下的加速度。通过该方法，可将最终的计算工况变成64个，不仅大大减少了计算量，而且对计算结果影响不大。

表1 浪向为090°和270°工况下加速度的组合方式

2.4 边界条件的模拟

2.4.1 运输时的边界条件问题

在处理边界条件时需考虑其真实的受力情况，大型导管架的装船步骤（见图4）一般为：

1) 通过滑道缓慢滑移至驳船上，移到指定位置停下；

2) 安装紧固件，将紧固件的一端与导管架的主腿焊接，另一端与驳船的甲板焊接，以保证能承受侧向载荷（见图5）。

从安装过程中可发现2个关键的边界问题，即：下水支架只承受压力（即重力）而不承受拉力；紧固件在安装过程中不承受重力，只在运动过程中承受惯性力。绝大部分的工程计算都没有考虑这种边界条件，本文以业内普遍做法为基础，结合工程经验对这种边界条件的模拟进行研究。

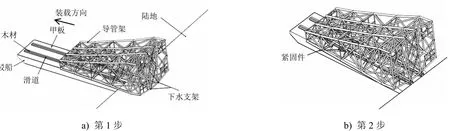
图4 导管架装船示意

2.4.2 边界条件的处理

对于下水架，木块和滑道可用一根杆件进行模拟，该杆件布置在主腿上的每个强节点（硬点）上，同时将该杆件设置为gap element（属性设置为只承受压力）。通过这样处理，将连续的滑道变成沿主腿分布的有限对只承受压力的支撑。

对于紧固件，因其独有的结构形状和受力方式，需对其进行特别考虑。首先，为方便焊接和切割，紧固件的两端各焊接一块板，该板与甲板和主腿直接焊接。由于该板承受面外弯矩的能力很弱，因此需进行自由度释放，使其不受面外弯矩（见图5）。基于该特点，在分析时应特别考虑下水支架是否会脱离滑道，即紧固件是否会产生面外弯矩。同时，考虑其受力过程，需用2个模型，其中：第1个模型中结构只承受重力，这时可将紧固件设置成 gap element (属性设置为只承受拉力) ，同时刚度设一个极小值（如 0.1），这样做相当于紧固件没有受力；第2个模型将紧固件设置为正常状态，以承受惯性力。

2.5 计算流程

1) 使用第1个模型，计算只有下水支架支撑时的受力情况（即图 1中的正浮工况）。将结构自重与其他附属构件的重力相结合并考虑一定安全系数之后生成总力（如STWZ）。计算时，将紧固件设置成只承受拉伸的单元，以模拟装船后未通过紧固件固定时的边界条件。

2) 使用第2个模型，生成惯性力（即图1中重力分量与运动惯性力的组合），首先将主体结构与附属结构的质量相结合并考虑一定的系数（与第一步相同）之后得到总质量，再通过该总质量计算惯性力，如表1中浪向为090°时可得出8种工况（0901，0902，0903，0904等）

3) 判断下水支架只有重力的情况下受到惯性力是否会脱离滑道（若脱离，则是危险工况，需特别考虑相应脱离点）。由步骤1)可知图 5中的A点只受重力的反力，将该力读出并加到B点，方向沿z轴向下，对其他支撑作类似处理，便得到一个工况（RACT）。将该工况与步骤2)中的工况组合，得到组合工况090A、090B、090C、090D等（即090A=0901+RACT，090B=0902+RACT等），这样由边界点反力便可知道在惯性力作用下下水支架是否还与滑道紧密相贴。

4) 惯性力与重力组合。该步骤是对前面计算的力进行线性叠加，得到新的工况 090I、090J、090K、090L等（即090I=STWZ+090A-RACT）。

5) 根据要求的规范进行杆件强度和节点强度校核，同时通过读取紧固件的杆端力对焊接强度和甲板强度进行校核。

图5 滑道和紧固件简图

3 工程算例与验证

工程算例基于MOSES软件和SACS软件对驳船与导管架组成的系统进行分析，侧重于分析导管架的强度相关问题。在导管架分析中，UC值可综合体现节点和杆件的强度与刚度，在工程中应用广泛，因此该算例可用UC值来衡量结构的性能。

3.1 环境条件

风速为13.95m/s（10m高处的风速）；波浪高Hs为4.50m，谱峰周期Tp为9～12s；流速为0.33m/s。出于保守考虑，风和浪同向。

3.2 总体布置图

总体布置模型（MOSES软件模型）见图6。

图6 总体布置模型（MOSES软件模型）

3.3 相关参数

驳船和导管架相关系数见表2。

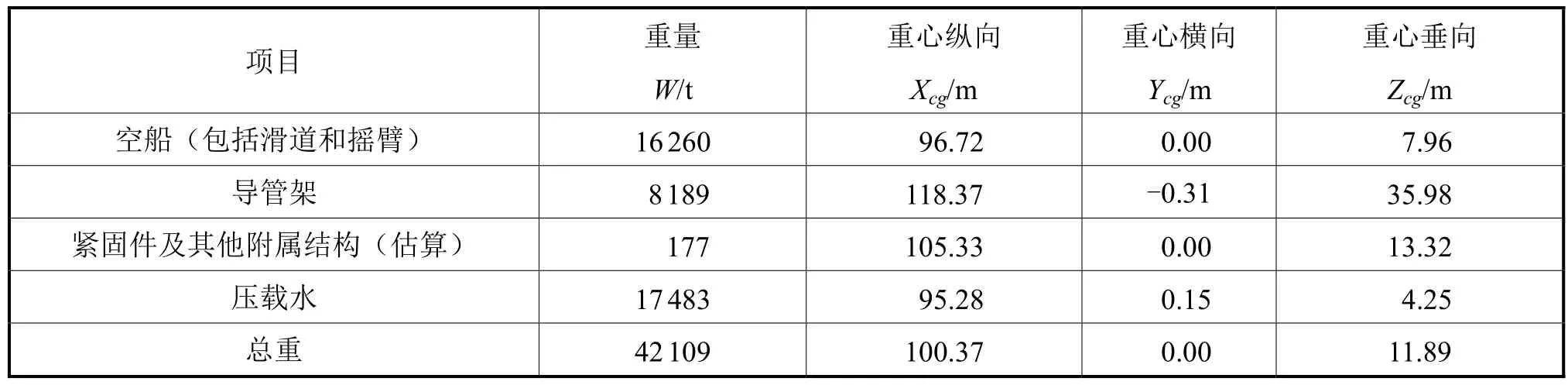
表2 驳船和导管架相关参数

3.4 运动计算结果

导管架重心的运动参数见表 3，列出的是考虑重力分量的总惯性力。考虑结构不对称的影响，在实际操作中可取对应方向的极值，如浪向为090°和270°工况下，运动参数只取两者之中的大值（如横摇取2.787，纵摇取0.428，以此类推）。

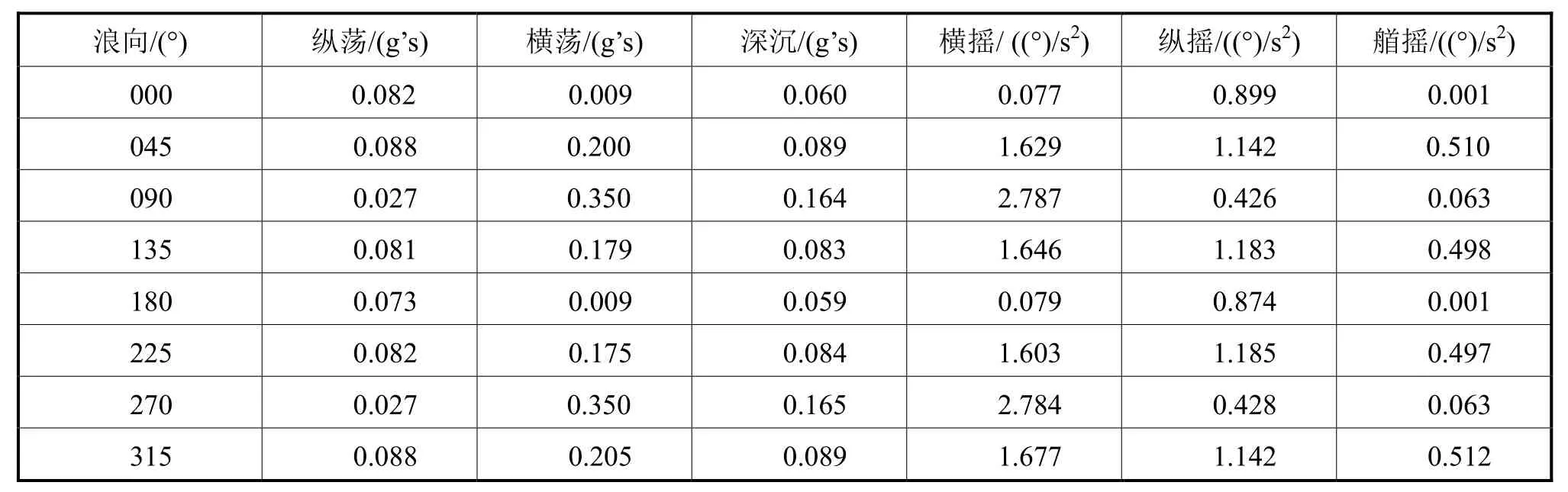
表3 导管架重心的运动参数

3.5 计算结果验证与分析

在导管架的运输分析中，关心主节点、紧固件和主结构等3种结构的UC值。该算例首先对512种工况进行计算，并整理出各方向的UC值和总体的UC值，同时分别与本文推荐的方法相对比。在数据处理中，将对应角度（如000°和180°，045°和225°）的浪向角归为1种工况，找出在该工况下最极端的结构。由于在不同浪向角下波浪载荷影响的结构不一样，因此每种工况下的危险结构不尽相同。但是，在同一种工况下最危险的结构相同，只是在数值上有一定差异。为方便起见，在以下分析中用UC1代表所有工况的计算结果，用UC2代表选择工况的计算结果。

3.5.1 主节点的比较

主节点比较见表4。由表4可知，选择工况的计算结果与所有工况计算结果之间的差别不大，说明在主节点强度上选择工况能较好地模拟出最极端的节点受力。

表4 主节点比较

3.5.2 紧固件的比较

主要杆件强度校核见表5。由表5可知，除了090°和270°，其他角度上UC1与UC2存在一定的差异，选择工况并不能很好地体现这些角度下的紧固件受力情况。

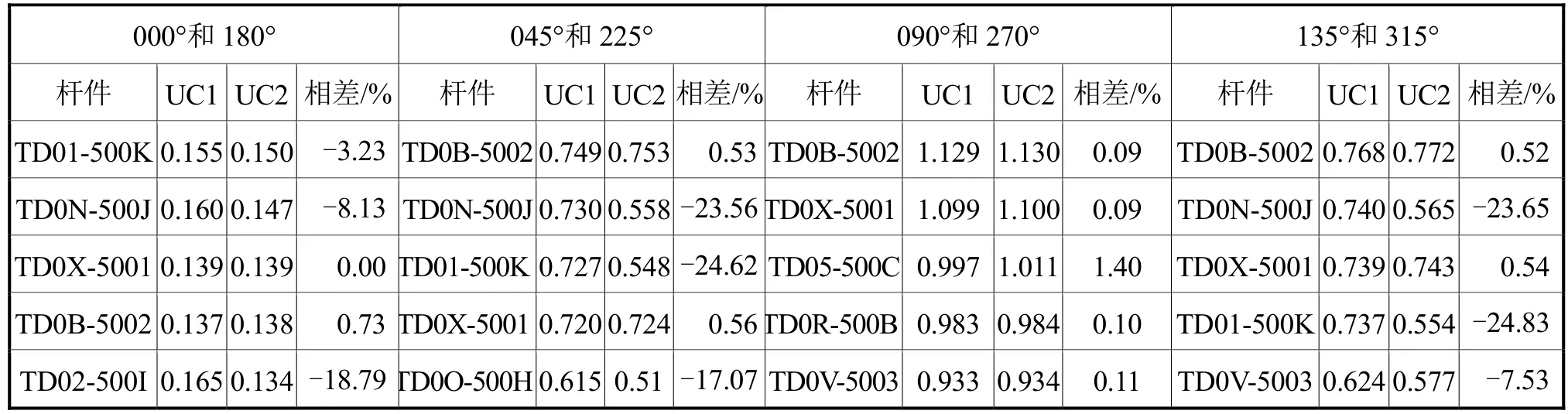
表5 主要杆件强度校核

3.5.3 主结构的比较

主结构强度校核见表6。由表6可知，UC1与UC2除了少数几根杆件以外，其余杆件相差不大，说明选择工况都能较好地预测主要杆件的受力情况。

表6 主结构强度校核

3.5.4 总体校核

对所有512种工况和选择的64种工况的计算结果进行整理，得到总的运输校核结果见表7。

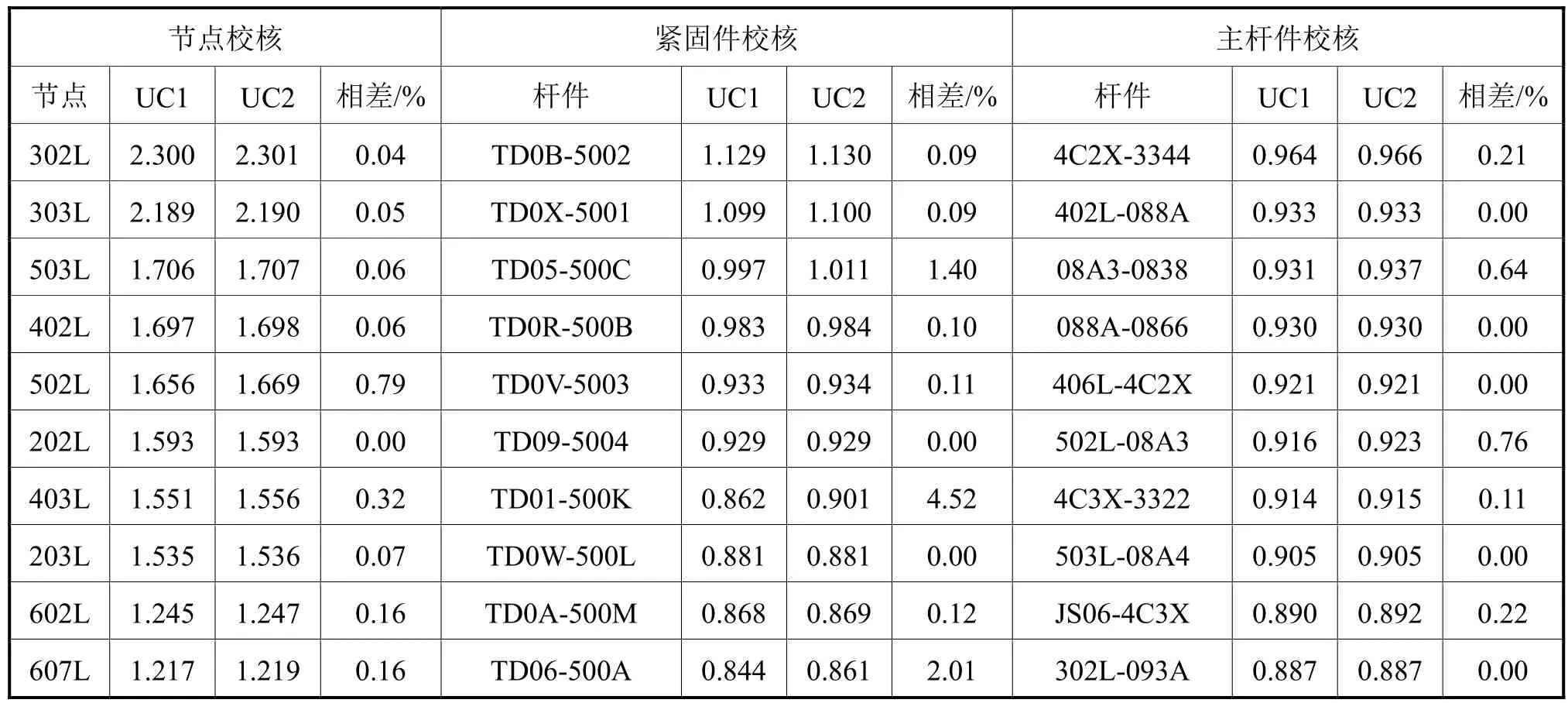
表7 总体校核结果比较

由表7可知，UC1与UC2相差不大，说明选择工况能很好地模拟结构最极端的受力状况。更进一步发现，无论是选择的64种工况还是所有512种工况，最极端的情况都出现在090°和270°，而选择工况在这2个方向上是吻合的最好的。许多工程计算都只考虑090°和270°工况，这时可只计算16种工况，且能得出较准确的结果。

4 结 语

本文以工程实例为基础，介绍导管架运输分析的基本原理；针对目前导管架运输分析过于保守的问题，提出一种新的计算方法。选择需计算的工况，将原本需计算的512种工况减少到64种，大大减少了计算量。通过与512种工况相对比发现，选择工况能很好地选出最危险结构位置并体现出危险程度。同时，通过对导管架实际安装运输流程进行分析，针对目前多数导管架分析中边界条件设置不合理的问题，提出了更为合理的边界条件，整理出了一份计算流程。

本文采用的计算原理、计算方法和边界条件等都可推广应用到半潜式、Spar等大型海洋工程结构物的运输方案设计中。