基于动力学分析的高速铁路空间线型振动敏感点分析

刘阳光，易思蓉，许健雄

(1.西南交通大学土木工程学院，成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

线路是列车的运行轨迹，是构造物的中心线[1]。随着高速列车运营速度的不断提高，机车车辆和轨道之间的振动强度也不断加剧，轮轨之间的动力学相互作用引起广泛的关注[2-4]。尤其是在高速线路直线段和曲线段连接点(如直缓点、缓圆点、圆缓点、缓直点)处，由于线路曲率及超高等的突然变化，车轮与轨道之间的动力作用发生突变而导致车体剧烈振动。由于我国高速铁路建设时间较晚，线路设计参数往往是在借鉴国外高速铁路设计经验的基础上依靠经验估算确定，没有考虑轮轨系统之间的相互作用。因此，对高速铁路空间线型振动敏感点进行动力学分析显得很有必要。

1 车-线耦合系统动力学模型的建立

运用SIMPACK动力学仿真软件，建立车线耦合系统动力学模型[5]。采用CRH2-300动车组的基本结构及参数为模型的基础数据[6-9]，对车-线耦合动力学模型进行抽象与简化[10-13]，将模型抽象为3部分：车辆模型、线路(轨道)模型以及轮轨接触关系。

进行车辆建模时，由于本文主要研究高速车辆的轮轨动力性能，因此在对车辆系统进行简化时，不考虑机车车辆中复杂的机械及电气系统。简化后，按从上到下的顺序，单节高速车辆主要由1个车体、2个转向架和4个轮对组成，车体和转向架之间通过二系悬挂装置连接，转向架和轮对之间通过一系悬挂系统连接。

线路(轨道)模型采用无砟轨道模型，并通过SIMPACK中的Track(轨道)模块对线路各参数进行设置，建立各工况的线路模型。采用LMA磨耗性车轮踏面和CHN60标准钢轨，通过Matlab编程，将LMA车轮踏面和CHN60钢轨外形进行数据离散，应用SIMAPCK软件提供的程序制作成程序可识别的LMA.wp和CHN60.rp文件；考虑车体仿真速度为250、300、350 km/h，参考文献[3]中分析内容，采用德国高速铁路低干扰谱，建立轨道方向不平顺和垂向不平顺，波长范围取1～45 m。

线路条件相同时，比较3节编组模型与8节编组模型，两者仿真结果差异甚微，但建模及数值积分时间却相差甚远，且3节编组模型能够很好地反映车体振动特性，因此采用3节车(动-拖-动)编组模型对于大量线路工况模型计算十分有利。建立3节车模型进行仿真计算，模型车体之间车钩缓冲器简化为具有三维方向的弹簧和阻尼，即无初始长度的“cmp”类紧凑力元，缓冲器为单一方向的弹簧和阻尼，即有初始长度的“ptp”类力元，二者并联联结，试验模型如图1所示。

图1 3节车编组(M-T-M)仿真模型

为保证模型的正确性及仿真试验的可信度，采用单次积分法计算模型的非线性临界速度对模型进行验证。通过验证，仿真车辆动车和拖车的非线性临界速度[550、600 km/h]、[500、550 km/h]区间内，且均大于500 km/h，远大于试验仿真运行速度350 km/h，可用于本次试验仿真。

2 仿真模拟工况

根据高速铁路曲线参数对车线动力学影响分析的相关研究，结合我国现行高速铁路设计规范[14]，在研究空间线型振动敏感点的振动规律时，车体仿真速度取250、300、350 km/h三档。为保证车体在圆缓点处产生的振动完全衰减，从而避免与缓直点处车体振动产生叠加，在设置线路工况时，仿真工况中曲线外轨超高、曲线半径及缓和曲线长度等参数取值如表1所示，轨道采用无砟轨道结构，并计算得出各种工况下，线路对应的均衡超高值如表2所示。

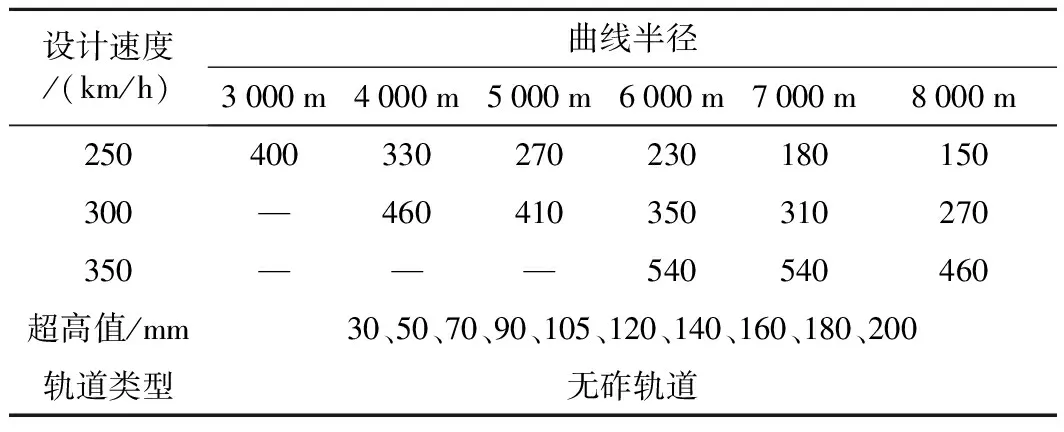
表1 仿真模拟线路不同速度、曲线半径对应的缓和曲线长度 m

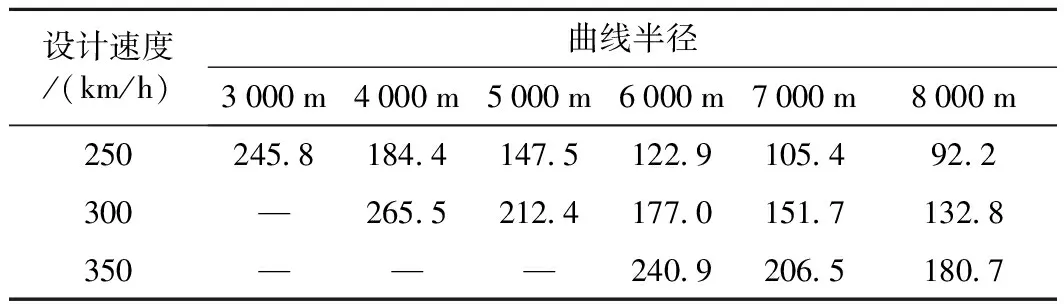
表2 不同速度、曲线半径对应的均衡超高 mm

3 计算结果分析

分析列车在设计速度250、300、350 km/h条件下，在不同曲线半径及不同超高情况下的车体横向及垂向振动幅值的仿真时程曲线，计算并统计出各种工况下车体振动衰减的数据。由于高速车辆运行过程中振动始终存在，故以车体第三节车(动车)在线路缓直点处加速度产生突变值，至车体振动加速度衰减至与列车在直线部分稳态运行振动状态相同时的时间，作为车体在振动敏感点处的振动衰减时间。各种工况下在缓直点处横向及垂向振动衰减时间如图2～图7所示。

3.1 缓直点的车体横向振动的衰减规律

如图2～图4可知，速度和超高一定时，车体横向振动衰减时间随曲线半径的增大而呈现增大的趋势，且有一定波动，当实设超高达到一定的高度时，横向振动衰减时间受曲线半径影响不大；当速度和曲线半径一定时，车体横向振动衰减时间随超高的增大呈上升趋势，且出现一定波动，最大值出现在均衡超高附近。

图2 缓直点引起的车体横向振动的衰减时间(V=250 km/h)

图3 缓直点引起的车体横向振动的衰减时间(V=300 km/h)

图4 缓直点引起的车体横向振动的衰减时间(V=350 km/h)

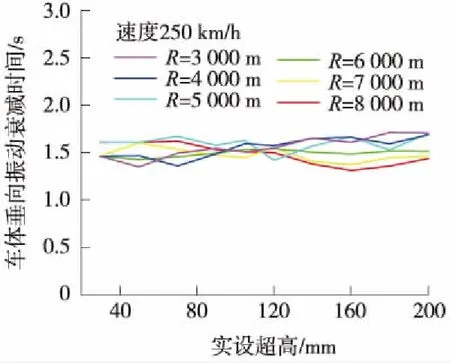
图5 缓直点引起的车体垂向振动的衰减时间(V=250 km/h)

图6 缓直点引起的车体垂向振动的衰减时间(V=300 km/h)

图7 缓直点引起的车体垂向振动的衰减时间(V=350 km/h)

3.2 缓直点引起的车体垂向振动的衰减规律

分析图5～图7，可以看出，当设计速度V=250 km/h，车体垂向振动衰减时间与圆曲线半径及曲线超高间的相关性较小，振动衰减曲线基本保持水平，并出现一定的波动，但波动范围较小；V=300 km/h时，车体垂向振动衰减时间随实设超高的增大呈上升趋势，但与曲线半径没有显著关系，振动衰减曲线整体呈上升趋势，并伴随有波动；V=350 km/h时，车体垂向振动衰减时间随实设超高的增大呈明显的上升趋势，曲线半径的影响仍不显著，振动衰减曲线整体呈明显的上升趋势，并伴随有较小的波动。

3.3 缓直点引起的车体振动的衰减时间统计分析

进一步对车体横向及垂向振动衰减时间的数据进行统计分析，得到车体在缓直点处产生的横向及垂向振动衰减时间的最大值、最小值、平均值，如表3、表4所示。

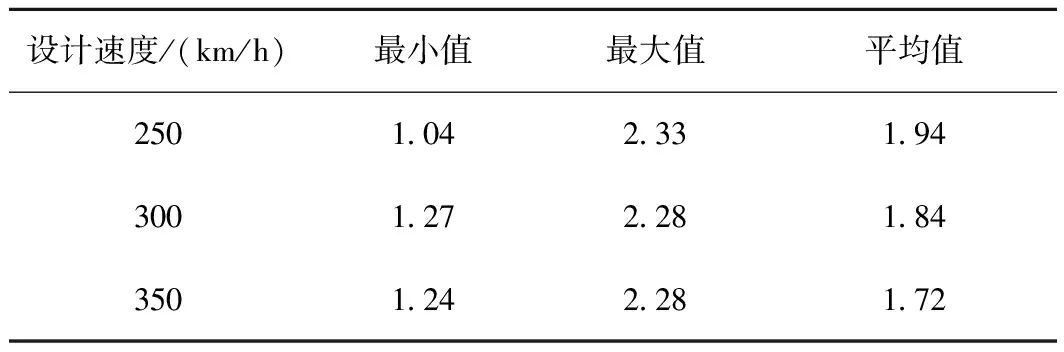
表3 缓直点引起的车体横向振动的衰减时间 s

表4 缓直点引起的车体垂向振动的衰减时间 s

3.4 缓直点引起的车体振动的衰减距离计算

根据振动不叠加原理，车体横向及垂向衰减距离

L=Vmax·T

式中，Vmax为设计速度，T为振动衰减时间。

结合表3、表4可得车体在缓直点处产生的横向及垂向振动均衰减完全所需的最小距离，如表5所示。

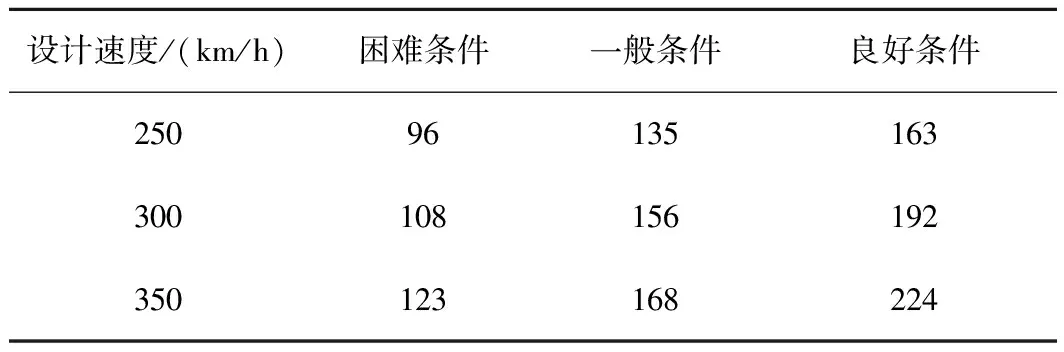
表5 缓直点引起的车体振动的衰减最小距离 m

4 结论

(1)速度一定时，随着曲线半径、实设超高的增大，车体横向振动衰减时间增加，在均衡超高附近取得最大值；车体垂向振动衰减时间随着实设超高的增大而增大，与曲线半径没有表现出明显的关系；并且均出现一定范围的波动。

(2)车体横向振动衰减时间普遍较垂向振动衰减时间长，不同速度下车体横向、垂向振动衰减时间差别均较小，故衰减距离主要由车体横向振动衰减情况决定。

(3)为避免高速列车振动叠加影响乘坐舒适性及行车安全性，线路相邻的两平面曲线以及相邻平面曲线与竖曲线之间的最小距离不应小于100 m，线路条件较好的情况下不宜小于230 m。