存在关节力矩输出死区及外部干扰的漂浮基空间机械臂积分滑模神经网络自适应控制
黄小琴, 陈 力
(1.福州大学 机械工程及自动化学院,福州350116;2.福建省高端装备制造协同创新中心,福州350116)
1 引 言
空间机械臂作为航天领域的关键技术之一,能够协助或代替宇航员完成极端空间环境中的一些舱外活动,如维护和修理故障卫星以及补给航天飞行器的物资等,对航天技术的进步发挥着愈来愈重要的作用,因此其系统动力学与控制问题的研究受到密切关注[1-5]。文献[6]描述了空间机械臂在时间延迟工况下,笛卡尔空间轨迹跟踪的控制方法。文献[7]研究了空间机器人系统捕获目标卫星时的冲击影响及随后的稳定控制问题。
死区、摩擦及饱和等非线性现象存在于空间机械臂执行机构的动力传递链中,这些现象大部分是未知且时变的,对控制精度造成很大的影响。其中,关节力矩输出死区作为一种重要的非线性现象,已经成为高精度传动控制的一个重点研究内容。但以往的研究往往没有考虑关节力矩输出死区对空间机械臂系统控制的影响,如果不能消除关节力矩输出死区的影响,除了会影响跟踪误差外,系统还会产生极限环振荡,导致性能下降或不稳定,从而无法完成空间任务。因此,研究带有关节力矩输出死区的空间机械臂具有重要的现实意义。在地面基机器人的控制研究中,已有学者考量了死区的效应[8-11]。文献[12]采用了基于 RBF的前馈网络补偿系统的非线性耦合控制;文献[13]设计了一种用于死区参数修正的智能补偿滑模控制方法;文献[14]结合死区观测器,研究了递归小脑网络控制器。同时,空间机械臂不可避免地会受到运动噪声、太阳风和宇宙射线等干扰因素的影响。综上,关节力矩输出死区与外部干扰都必须在研究中加以考虑。
本文在前述研究的基础上,针对带有关节力矩输出死区及外部干扰的空间机械臂系统建立动力学方程。通过构造关节力矩输出死区的模型和积分切换函数,借助增广变量法,提出一种积分滑模神经网络的控制算法。在死区斜率与边界参数不确定及最优逼近误差上确界未知的条件下,利用最优逼近误差、死区及干扰的补偿项来克服各自的影响。稳定性分析和仿真实验表明本文控制方法有效。
2 系统动力学模型
图1为自由漂浮的双杆空间机械臂系统,根据第二类拉格朗日方程,可以得到其载体位置和姿态都不受控的动力学方程[6]:
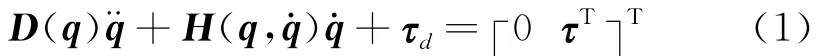
式中 D(q)∈R3×3为对称正定的质量矩阵,H(q,∈R3为包含科氏力和离心力的列向量,τd∈R3为外部扰动列向量,τ∈R2为机械臂两关节铰控制力矩τ1和τ2组成的列向量,q∈R3为载体姿态角α0及关节角θ1和θ2组成的广义坐标向量。
3 关节力矩输出死区及其基本性质
对于很多物理装置,在输入的大小达到某个特定值之前,其输出为0。这种输入-输出关系称为死区。从反馈控制的观点出发,死区可认为是信息丢失。空间机械臂系统的关节力矩输出可能含有死区特性。本文考虑如图2所示的典型的死区模型[15],死区输入为ur(t)= [ur1(t),ur2(t)]T,输出为τ。
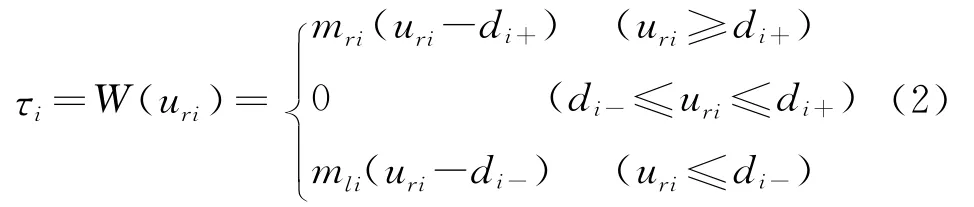
式中di-和di+,mli和mri分别为死区的左右断点与左右斜率,设定mri=mli=mzi。死区参数di-,di+和mzi为有界不确定量,且di+>0,di-<0,mzi>0。
把死区模型改写为
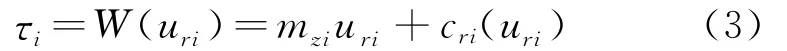
式中

cri(uri)≤βi,其中βi是有界的。
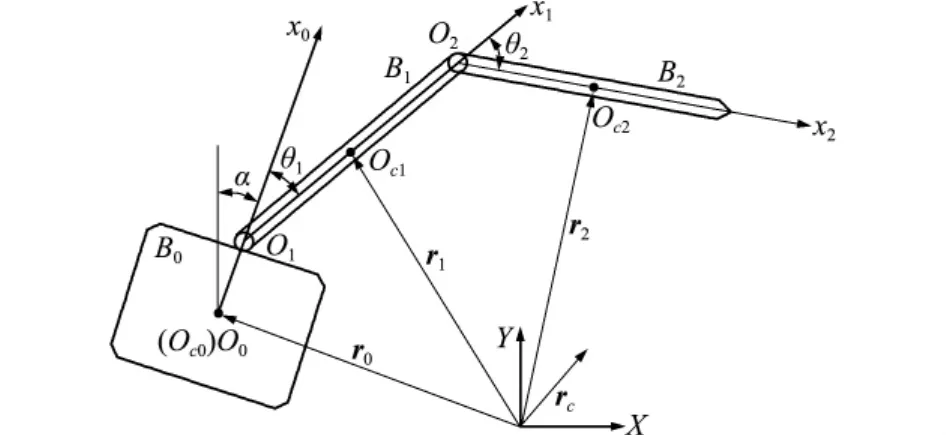
图1 漂浮基双杆空间机械臂系统Fig.1 Free-floating space robot system
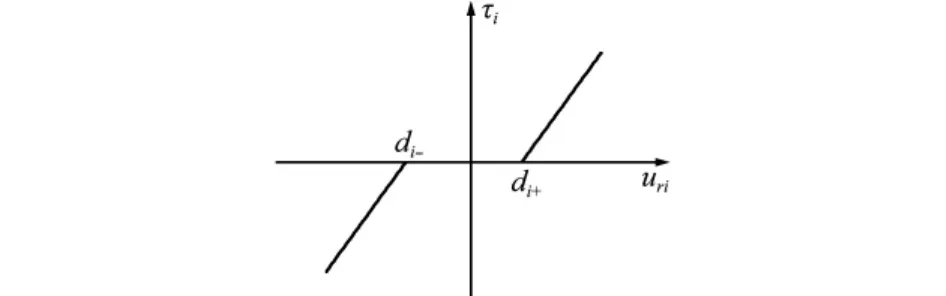
图2 关节力矩输出死区模型Fig.2 Joint torque output model with the dead-zone
4 抗关节力矩输出死区及外部干扰的积分滑模神经网络自适应控制
4.1 径向基函数神经网络及其函数逼近
径向基函数神经网络是一种三层网络,通过局部逼近的总和来实现全局逼近[16]。对各类强非线性函数具有良好的逼近能力,能够以任意精度逼近连续非线性函数,且具有学习速度快和能避免局部极小问题的优点。因此,本文采用此类神经网络进行控制器设计,其结构示意图如图3所示。
用径向基神经网络来逼近系统输出f(x),即
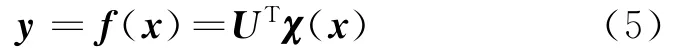
式中 x=[x1,x2,…,xr]T为神经网络系统的输入,χ(x)=[χ1,χ2…,χn]T为基函数列向量,UT=[uij](i=1,…,l;j=1,…,n)为网络权值矩阵,y=[y1,y2…,yl]T为输出列向量。
采用的基函数为高斯函数,则χ(x)的元素可表示为
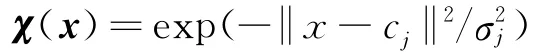
式中cj为第j个基函数的中心位置参数,σj为第j个基函数的宽度参数。
4.2 控制器设计
设计空间机械臂的控制方案时,对载体的位置和姿态都不施加控制,可减少能源的损耗,延长其工作寿命。
此时,系统控制输出为qr=[θ1θ2]T,而q∈R3。显然,该控制输出向量的维数小于后者,从而难以继续利用式(1)及其相关性质进行后面相关控制器设计。为此,本文引入增广变量思想来解决这一难点。
将式(3)代入式(1),将其写为状态方程的形式为


图3 径向基神经网络三层结构示意图Fig.3 Three-layer radial basis function neural network
式中 x1=q,x·1=x2=q·,N=D-1(x1)u(t),g(x1,x2)=-D-1(x1)H(x1,x2)x2为未知的有界连续函数,h(x1,x2,t)=-D-1(x1)[c(u)-τd]为系统的外来干扰和死区特性,c(u)=[0,crT(u)]T为执行机构的死区特性,mz=diag(0,mz1,mz2)为死区斜率矩阵,u=[0,urT]T为增广关节力矩死区输入。
设期望输出为qrd=[θ1d,θ2d]T,则增广期望输出为qd=[α0d,]T,那么增广误差为
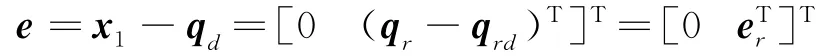
式中er=qr-qrd=[(θ1-θ1d) (θ2-θ2d)]T=[e1e2]T
控制目标是设计关节力矩控制律N,让两关节的qr稳定地跟踪qrd。
定义具有积分的增广切换函数:
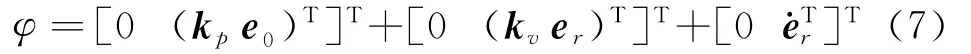
式中
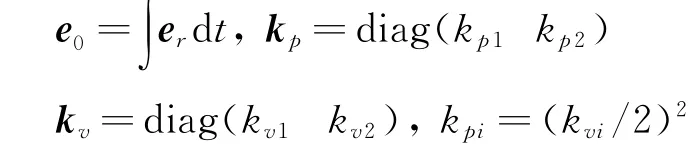
常数kvi>0。
定义光滑函数为Yφ(t)=φT(t)Γφ(t)
式中 Γ=diag[0 1/mz11/mz2]
对Yφ(t)关于时间t求导可得
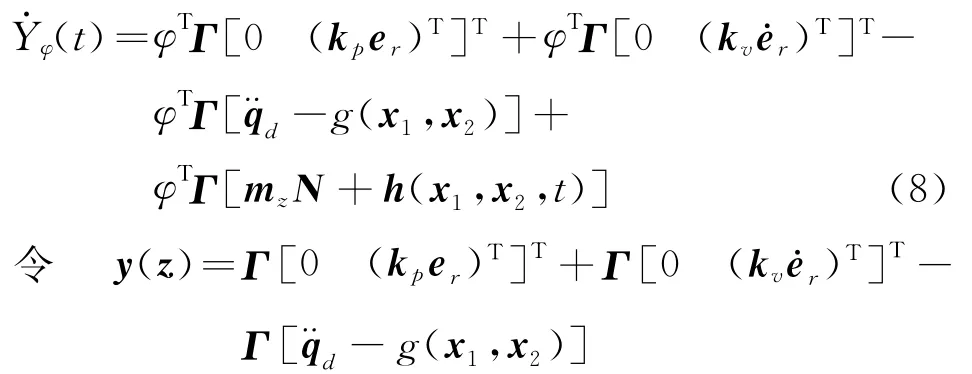
因为g(x1,x2)和死区斜率未知,则y(z)未知,根据前述神经网络式(5)来逼近y(z),设y(z U)为y(z)的一个逼近,即
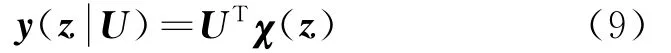
式中 UT=[uij](i=1,…,n;j=1,…,m)为网络权值矩阵,χ(z)=[χ1,…,χm]T为基函数列向量,m为基函数中心点个数,y=[y1,…,yn]T为输出列向量。
χ(z)的元素为高斯基函数,可表示为
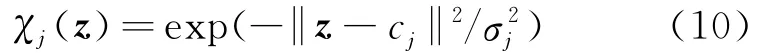
U*为U的最优值,并满足
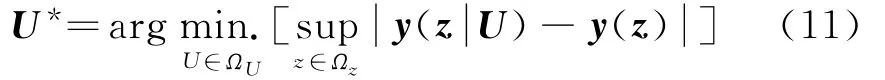
式中 ΩU= {U‖U‖≤MU},设计参数MU为正的有界常数,Ωz= {(xT,ρ)T‖x‖≤Mx},Mx>0。
令
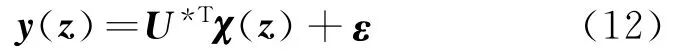
式中ε∈R3为最优逼近误差,‖εi‖≤εyi,εyi为正常数。
由式(9~12),可得
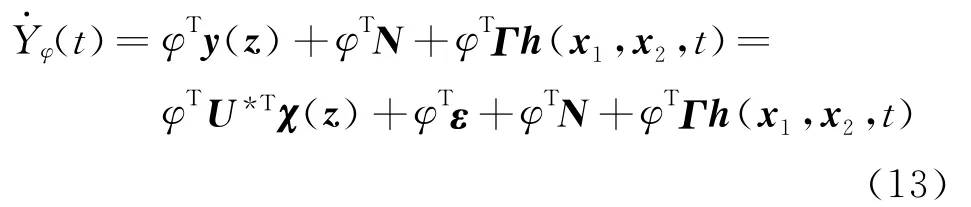
式中 ‖hi(x1,x2,t)‖≤Ξi,Ξi为已知的正连续函数。
设计如下控制律,
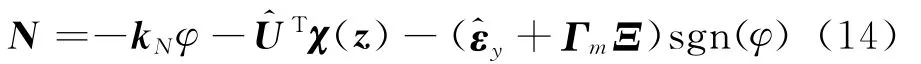
式中 kN∈R3×3为正的设计参数,Γm=diag[0,1/mz1min,1/mz2min],mzimin为死区斜率 mzi的最小值,和分别为U*和εy在t时刻的估计值。
定理 对于式(6)所示的系统,采用式(15)的关节力矩控制规律及如下参数自适应调节率,
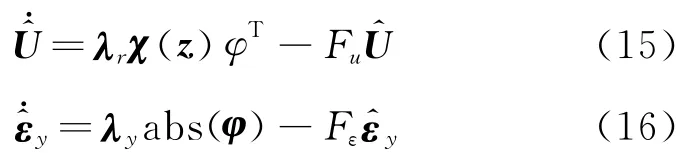
将使积分切换函数φ有界,且轨迹跟踪误差收敛到0。式中 λr=diag[λr0λr1λr2λr3λr4]和λy=diag[λy0λy1λy2]为正定自适应调节矩阵,Fu和Fε为正常数,abs(φ)为列向量φ中每一项取绝对值。
证明 构造李雅普诺夫函数:
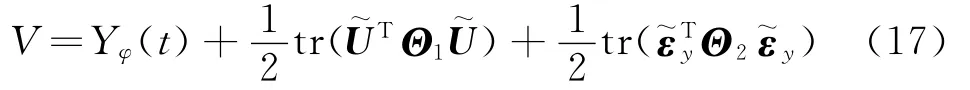
式中
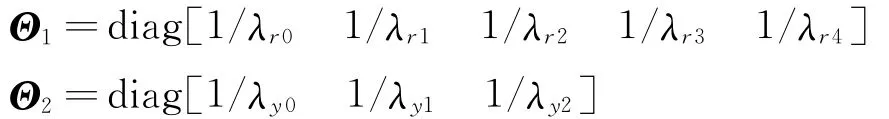
V对时间t求一阶导为
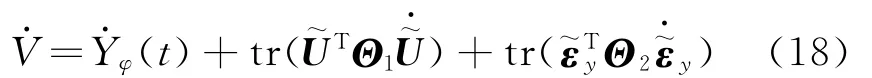
将式(13)代入式(18),即

将‖εi‖≤εyi和‖hi(x1,x2,t)‖≤Ξi代入式(19),得
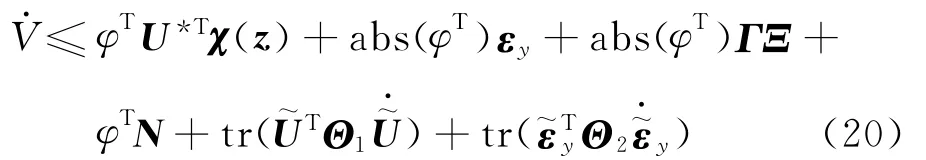
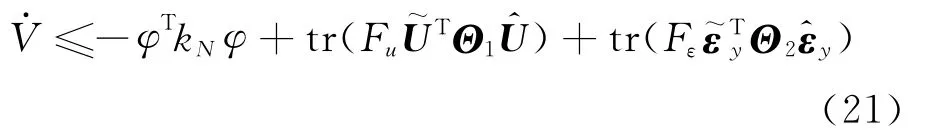
利用不等式
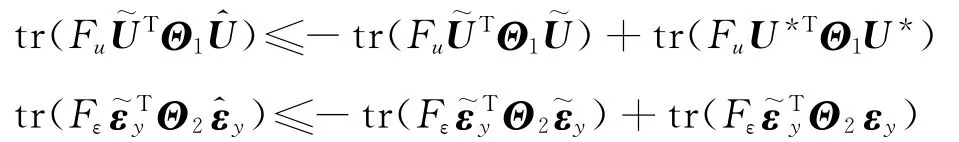
代入不等式(21),得
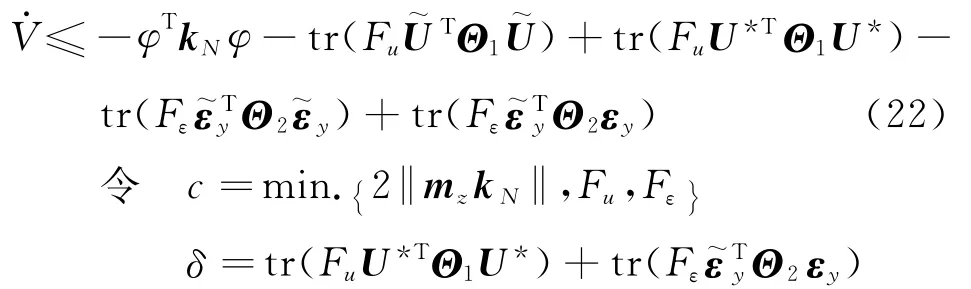
可得

不等式两边同乘ect,并从[0,t]积分可得
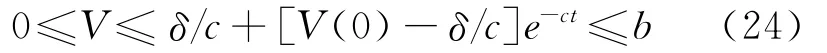
式中 b=δ/c+V(0)。
因此,V有界,从而φ也有界。选取合适的数值,将使δ/c充分小。因此,跟踪误差收敛到0的某个小邻域内,定理得证。
5 仿真算例
为验证前述所设计控制算法的有效性,采用如图1所示模型进行验证。取系统惯性参数l0=1.5 m,l1=l2=1m,m0=40kg,m1=2kg,m2=1kg。中心惯量矩J0=34.17kg·m2,J1=J2=1.5kg·m2。
选取qrd为
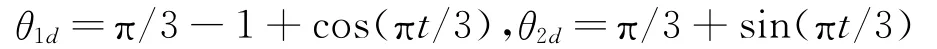
系统的外部干扰取为
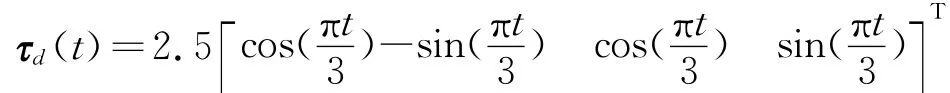
仿真时,系统参数矩阵选择如下,
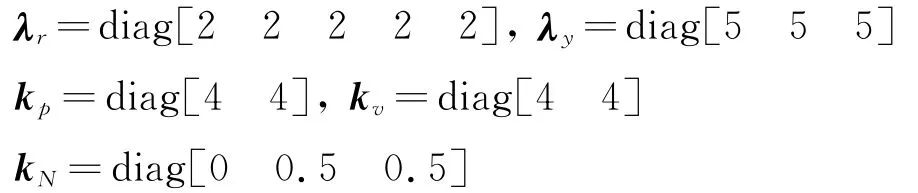
神经网络径向基函数的参数取值:基函数的个数j=5,基函数的中心位置参数cj根据神经网络输入的范围取值,其宽度σj设置为5。
死区参数为d1-=d2-=-10,d1+=d2+=10,mz1=mz2=1,mz1min=mz2min=0.85。
仿真初始值q(0)=[3 0.5 1.5]T,(0)取0~0.1的随机数,(0)=[000]T。
仿真时间取t=10s。图4和图5分别为采用积分滑模神经网络自适应控制算法得到的存在关节力矩输出死区与外部干扰的空间机械臂两关节铰的qr与qrd及其跟踪误差的对比情况,其中图4还显示了载体姿态的轨迹变化。可以看出,控制算法虽然没有控制载体姿态,但其姿态变化平稳;两关节铰的qr能很好地跟踪上qrd,在t=4s之后基本消除误差,具有较高的跟踪精度。
为对比控制方法的有效性,图6给出了关闭死区补偿控制器后,空间机械臂两关节铰的实际运动与期望轨迹变化仿真。可以看出,关闭死区补偿,两关节铰无法跟踪qrd。

图4 开启死区补偿器时的轨迹跟踪图Fig.4 Trajectory tracking of the space manipulator

图5 开启死区补偿器时两关节铰的轨迹跟踪误差图Fig.5 Trajectory error tracking of the two joints(open dead-zone compensation)
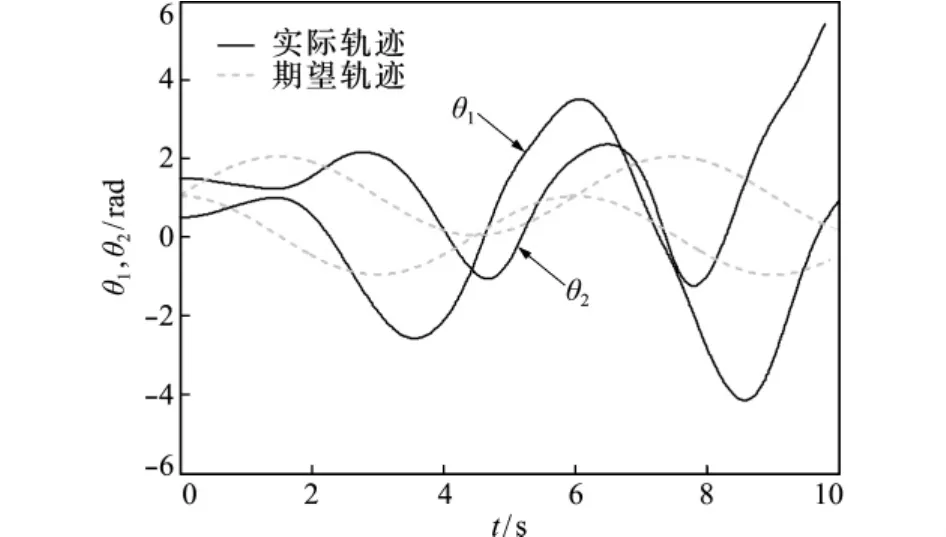
图6 关闭死区补偿器时两关节铰的轨迹跟踪图Fig.6 Trajectory tracking of the two arms’joints(closed dead-zone compensation)
6 结 论
本文针对空间机械臂存在关节力矩输出死区及外部干扰的情况,建立了带有外部干扰的动力学方程。通过构造关节力矩输出死区的模型,设计了一种积分滑模神经网络自适应控制方法。具有积分的切换函数减小了系统稳态误差;利用神经网络逼近了动力学方程的未知部分;在死区斜率与边界参数不确定及最优逼近误差上确界未知的条件下,利用最优逼近误差、死区及干扰的补偿项来消除各自的影响;构造李雅普诺夫函数并证明了闭环系统是稳定的。

