基于各向异性损伤本构模型的砌体结构抗震分析

富秋实， 钱 江

（同济大学 土木工程与防灾国家重点实验室，上海200092）

1 引 言

砌体结构是土木工程中最古老的结构形式之一，为了有效地保护历史建筑遗产和人员生命安全，针对既有砌体结构的结构分析手段显得十分重要。一般，砌体结构分析主要是使用基于经验的分析方法。过去的几十年研究者对砌体结构的数值模拟方法进行了大量研究。另一方面，由于砌体材料特殊的各向异性性质，采用其他领域（如混凝土、岩石和复合材料）的数值模拟方法存在一定困难。所以，针对砌体的各向异性本构模型的研究开发具有重要意义。

在各向异性材料本构模型的研究领域，除了直接提出各种各向异性材料的屈服准则函数以及损伤准则函数［1］外，还有一类策略是采用基于应力张量分量线性变换（linear transformation）的方法。使用线性变换的方法便于保持屈服准则函数和损伤准则函数等的外凸性，这对于在实践中保持本构算法的数值稳定性十分重要。因此，这类方法得到了较为广泛的关注。为了有效地利用已有损伤理论，开发能够考虑砌体材料各向异性特性的损伤模型，本文采用基于应力张量线性变换的方法。

应力张量的线性变换方法最早由Sobotka［2］和Boehler等［3］提出。Barlat等［4，5］将各向同性屈服函数与线性变换后应力张量的主应力相结合，用于解决正交各向异性材料的平面应力问题，并将这一方法应用于三维应力状态。Karafillis等［6］将该方法推广为各向同性塑性等效IPE（isotropic plasticity equivalent）理论，将线性变换方法与更加一般化的屈服函数相结合，可用于其他类型的材料。Barlat等［7］使用该方法提出了基于应力偏量线性变换的各向异性屈服函数，用于模拟金属板在轧制方向和横向的各向异性塑性特性。

砌体材料各向异性本构模型的已有研究，除了直接提出各项异性屈服函数，也有应用张量线性变换方法的研究［8，9］。这些研究使用的方法称为映射张量法（mapped tensor method）。

映射张量法最早由Betten［10］提出，用于解决蠕变相关问题。其假设存在一个真实的应力空间和一个虚拟的应力空间，两个应力空间之间存在映射关系，由一个四阶映射张量定义。存在于真实应力空间的各向异性材料的受力状态可以映射到存在于虚拟应力空间的虚拟各向同性受力状态。可以看到，Betten的映射张量法的思想本质上与前文介绍的线性变换方法基本一致。Oller等［11，12］对这一映射张量法进行了进一步的发展。

本文进一步完善了应力张量的线性变换方法，提出了适应塑性以及损伤演化程度的动态线性变换张量，并将其应用于砌体材料本构模型的开发。利用该本构模型对砌体结构的振动台试验进行了模拟。模拟结果验证了本文提出的弹塑性损伤本构模型的有效性，以及在进行结构非线性分析方面的优越性。

2 动态变换张量

设四阶动态线性变换张量为Aσ，（Vk）， ∈｛p，d｝。内变量Vk是描述材料内部不可逆变化进程的变量，如塑性强化参数等。上标σ和p的含义为用于塑性本构的应力转换张量，σ和d的含义为用于损伤本构的应力转换张量。不同于已有的Oller和 Pelà模型［9，11，12］，本文并没有应变转换张量。但为了与文献的应变转换张量相区别，下文将依然保留上标中的σ。

根据应力转换张量的定义，有

式中σ＊为变换后的应力张量。设未知其具体表达的各向异性屈服／损伤面函数F为

设已知形式的各向同性本构的屈服函数和塑性势函数表达式为

此时根据定义显然有

即得到了未知函数F的隐式表达。另一方面，由于不同方向各向异性强化的特性记入变换张量Aσ，（Vk）中，因此随着强化参数Vk的演化，在F＊呈现各向同性强化的同时，F可以呈现各向异性强化。

3 各向异性弹塑性损伤模型建立

3.1 塑性演化

在以往研究中，对于混凝土等摩擦性材料的屈服函数一般采用 Mohr-Coulomb或Drucker-Prager屈服函数，但与试验结果并不是很接近。本节同时采用Rankine和Drucker-Prager形式的双屈服准则，模拟砌体材料受拉及受压屈服特性，基于动态线性变换张量，建立针对砌体材料的正交各向异性塑性修正方法。

（1）受拉Rankine形式屈服面

各向同性受拉屈服函数采用Rankine形式为

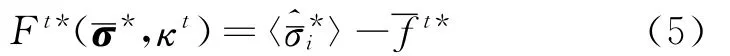
引入四阶受拉塑性转换张量Aσ，pt，则可由式（1～3）得到受拉Rankine形式屈服面的各向异性隐式表达。

（2）受压Drucker-Prager形式屈服面

各向同性受压屈服函数采用Drucker-Prager形式为

式中α为控制双轴受压强度特性的参数，单轴受压状态下有效应力阈值fc＊简化为硬化参数的线性函数。

引入四阶受压塑性转换张量Aσ，pc，可由式（1～3）得到受压Drucker-Prager形式屈服面的各向异性隐式表达。

3.2 损伤演化

为了反映在受拉和受压状态下材料的力学性能差异，损伤本构模型需要将应力张量σ［13］或者有效应力张量σ［14］分解为正负张量两部分。在基于应变的有限元分析中，应力张量σ在迭代收敛前是未知量，基于应力张量的分解会极大地增加计算量和数值计算难度。另一方面，由于有效应力张量σ和弹性应变张量εe线性相关，基于有效应力张量的分解更利于建立应变的显式表达。因此，本文采用有效应力张量的分解方法，建立损伤演化规则：

此外，损伤修正部分只需考虑弹性损伤力学模型，更新应力张量和损伤变量，而不需要考虑塑性变形的影响。因此，为了方便书写，下文的理论推导部分将省略弹性应变张量εe的上标e。

（1）受拉损伤演化

受拉状态下的各向同性损伤面函数采用Rankine形式：

τ＋＊具有应变张量的量纲，称为受拉等效应力。为方便计算，损伤各向同性受拉准则函数写为

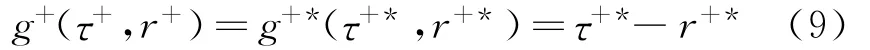
r＋＊为受拉各向同性损伤面函数对应的等效应力阈值。

（2）受压损伤演化

受压状态下的各向同性损伤面函数采用修正的八面体应力组合：

式中 参数K控制双轴受压状态有效应力损伤阈值与各方向单轴受压状态下有效应力损伤阈值的比值，其取值由试验确定。

（3）II型破坏损伤演化

砌块-砂浆界面的II型破坏尚难以用损伤变量d＋和d－来描述，其滑动破坏机制也与受拉及受压开裂有着明显的区别。根据内变量理论的概念，不同机制的不可逆过程应该由不同的内变量来表示。因此，本节在前文理论的基础上，直接引入一个损伤变量dII，来描述砌体材料灰缝的II型破坏。

首先，引入II型破坏等效应力：

式中σ12为沿灰缝滑动的剪应力，σ22为垂直于水平灰缝的正应力，II为II型破坏对应的摩擦角。相应的损伤准则函数为

式中r0，II为II型破坏等效应力的初始阈值，由剪切试验确定。假定II型破坏损伤变量的显式表达式为指数函数形式：

4 对比验证

同济大学于2011年对某砌体结构进行了振动台试验，该试验原型结构为上海市某临近地铁的住宅［15，16］。由于振动台试验的能力限制以及砌体结构模型试验的特殊性，试验采用局部代表性结构来模拟原型结构，从实际结构中取出三层两个房间作为代表性结构进行研究。由于代表性结构的质量（690t）依然远超出振动台的能力范围，所以本试验采用代表性结构1／4的缩尺模型进行振动台试验研究。

地震波加载方向为模型的横墙方向，即X向。模型砌体部分材料采用小砖块和砂浆，构造柱混凝土采用砂浆，钢筋采用镀锌铁丝，原型结构楼屋面厚度为110mm，1／4缩尺后楼屋面板厚为27.5mm，考虑到施加质量块时固定砂浆会对楼板有一定程度的加强，并且楼板并不是试验模拟的重点，为使楼板能够承受附加质量引起的合重，楼屋面板厚取40mm，混凝土部分用砂浆，钢筋采用镀锌铁丝进行模拟。砂浆浇注时用小振捣器振捣和小铁钎插捣，保证模型浇筑质量。模拟砌体部分的小砖块由MU10砖块在三个方向上一分为四，即每块砖切成64块模型小砖块，砂浆用M2.5混合砂浆。

4.1 计算模型概况

通过商业有限元程序ANSYS的Usermat子程序，将前文所建立的各向异性本构模型嵌入ANSYS程序中，用来进行砌体结构非线性分析。程序编写基于平面应力状态，可用于平面应力单元以及壳单元（平面应力＋板弯曲）。

利用ANSYS程序进行三维空间建模。砌体墙、楼板及模型底座采用SHELL单元模拟，混凝土梁和柱采用BEAM单元模拟。计算模型共计单元数3392，节点数3494。计算采用的主要材料参数为x向弹性模量E1＝1806MPa，抗拉强度＝0.6MPa，抗压强度＝4.8MPa；y向弹性模量E2＝1508MPa，抗拉强度＝0.4MPa，抗压强度f2－＝4.0MPa。计算模型如图1所示。

4.2 8度罕遇烈度El-Centro波作用下结构响应结果对比

为了尽可能使计算工况与试验工况保持一致，计算时的加速度输入采用相应工况的试验台面记录。

（1）楼层加速度对比

表1及图2为8度罕遇El-Centro波下，加速度试验与数值分析包络结果对比。

图3～图6为8度罕遇El-Centro波下，加速度试验与数值分析加速度时程结果对比。

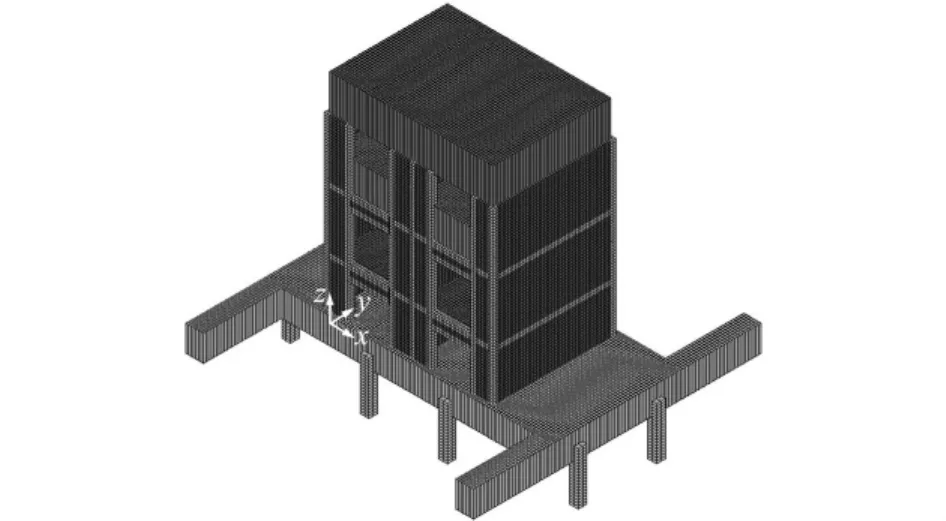
图1 有限元模型Fig.1 FEM model

表1 加速度试验与数值分析包络结果对比Tab.1 Comparison of acceleration results obtained from test and simulation

可以看出，除了模型底板处的动力响应结果与试验偏差略大以外，整体结构的相应幅值与试验结果比较接近；相位结果有一定偏差，其原因可能为计算模型未考虑混凝土底梁的非线性行为，但在试验过程中混凝土底梁进入了非线性状态。

图2 加速度试验与数值分析包络结果对比Fig.2 Comparison of acceleration results obtained from test and simulation

图3 一层加速度反应时程结果对比Fig.3 Comparison of acceleration time history curves of the first floor

图4 二层加速度反应时程结果对比Fig.4 Comparison of acceleration time history curves of the second floor

图5 三层加速度反应时程结果对比Fig.5 Comparison of acceleration time history curves of the third floor

图6 顶板层加速度反应时程结果对比Fig.6 Comparison of acceleration time history curves of the roof

（2）楼层相对位移对比

表2和图7为8度罕遇El-Centro波作用下，楼层相对位移试验与数值分析包络结果对比。两者结果除了2层处相差较远外，其他位置结果比较接近。考虑本模型在2层处没有附加质量和刚度突变，计算所得的位移包络曲线形状更加符合结构概念，因此，认为计算得到的结果具有较好的可信度。

（3）损伤分布情况对比

计算结构损伤分布情况如图8所示，损伤主要分布在模型的底层。试验结果显示，在8度罕遇El-Centro波作用下，试验模型主要破坏模式为横墙1／2高度处起始的斜向阶梯型裂缝（试验过程中能听到明显的开裂声音），相应的试验模型裂缝照片和计算模型损伤分布对比情况如图9所示，可见计算模型的损伤分布与试验模型裂缝开展情况基本相符。同时，纵墙的墙体底部也发生了较为轻微的水平开裂，试验模型裂缝照片和计算模型损伤分布对比情况如图10所示，两者结果也基本相符。

表2 楼层相对位移试验与数值分析包络结果对比Tab.2 Comparison of maximum story relative displacements

图7 楼层相对位移试验与数值分析包络结果对比Fig.7 Comparison of maximum story relative displacements

图8 计算模型整体损伤分布情况Fig.8 Damage distribution of FEM model

图9 底层横墙裂缝／损伤分布对比Fig.9 Crack／damage distribution of bottom lateral wall

5 结 论

本文进一步完善了应力张量的线性变换方法，提出了适应塑性以及损伤演化程度的动态线性变换张量，建立了以该变换张量为基础发展各向异性弹塑性本构模型以及损伤本构模型的一般方法，并将其应用于砌体材料本构模型的开发。

基于开发的砌体各向异性弹塑性损伤本构模型，本文对砌体结构的振动台试验进行了模拟。模拟结果进一步验证了本文提出的弹塑性损伤本构模型的有效性，以及在进行结构非线性分析方面的优越性，即除了能够获取结构的反应外，还能实时提供结构中的损伤分布状态信息，找出结构的薄弱部位，并据此合理地设计结构或进行相应的结构修复。