两性杂双子表面活性剂在水溶液中的自组装行为:耗散粒子动力学模拟
徐 毅,毛新建,郭思宇,冯 剑
(1.上海大学环境与化学工程学院,上海200444;2.滁州学院材料与化学工程学院,安徽滁州239000)
双子表面活性剂(又称Gemini表面活性剂、偶联表面活性剂等)是由联接基团将两个传统表面活性剂分子在其亲水头基处或附近的烷烃链上相连接而成的一类双头基双尾链的新型表面活性剂[1].由于结构上的特殊性,与传统表面活性剂相比,双子表面活性剂不但具有较低的临界胶束浓度(critical micelle concentration,CMC)、C20(表面张力比纯水降低20 mN·m-1时的浓度)值和临界胶束浓度处的表面张力γcmc,而且具有较高的表面活性以及较好的润湿性、可溶性、发泡性和钙-皂分散性等诸多独特的优良性能,从而使其在新材料制备[2]、增溶分散[3]、基因传输与转染[4]、三次采油[5]、金属防腐[6]、环境保护[7]等众多关乎国计民生的重要领域有较高的应用价值,因而也受到了国内外有关专家以及相关研究机构的高度关注.自1971年Bunton等[8]成功合成了第一类阳离子型双子表面活性剂以来,研究者们对于在分子结构上完全对称的双子表面活性剂已从理论、模拟和实验等各个方面开展了大量的研究工作,并取得了一系列令人瞩目的成果,从而加深了人们对于此类物质的理解与认识,同时也引发了人们对于具有不对称分子结构的双子表面活性剂的思考与探索.双子表面活剂最早出现于1996年[9],后被Alami等[10]专门命名为“heterogemini surfactant”,即“杂双子表面活性剂”,是指两个亲水头基不同或者两根疏水尾链不同的在分子结构上更为特殊的一类双子表面活性剂.分子结构所具有的明显不对称性往往直接导致其自组装行为表现得更为复杂.例如,Peresypkin等[11]发现CmH2m+1-PO4--(CH2)2-N+(CH3)2-CnH2n+1(简记为Cm-P-N-Cn,其中m,n=9,9;9,12;9,15;9,18;12,12;12,15;12,18;15,15;15,18;18,18)体系在稀溶液中形成了胶团、囊泡、小管等多种自组装结构,而其中最为特殊的是C8-P-N-C10和C8-P-N-C14两个体系所形成的海绵状凝聚层.Oda等[12]首先通过实验观测发现,疏水尾链的对称性是双子表面活性剂在水溶液中形成管状和层状结构的关键因素,而其对自组装结构的影响主要来自整个分子的不对称性所引起的曲率增加.其后,Menger等[13]通过系统研究得出了一张用于描述疏水尾链长度对Cm-P-N-Cn系列杂双子表面活性剂体系自组装行为影响的结构相图.Menger等[14]又通过进一步研究发现,Cm-P-N-Cn分子中的两根尾链之一进行分枝化后可相当“敏感地”影响其自组装行为.Menger等[15]很快又在实验中观察到:当m>n时,Cm-P-N-Cn系列物质在水溶液中不仅通过自组装形成了囊泡,还能够将众多的囊泡串接成“珍珠项链”状;而当m=n时,体系中就只有独立的囊泡,无串接行为.Nyuta等[16-17]则发现杂双子表面活性剂在水溶液中形成的聚集体尺度会随其分子中疏水尾链长度的增加而逐渐增大.Takamatsu等[18]发现疏水尾链长度的增加会使得杂双子表面活性剂在水溶液中的临界聚集浓度显著降低.Nyuta等[19]利用多种实验分析手段对含有两性离子的杂双子表面活性剂在水溶液中的聚集行为进行了研究,并重点考察了疏水尾链长度对其产生的影响,最终观察到了球状胶束、柱状胶束、囊泡、柱状胶束与囊泡共混体这4种自组装形态.Liu等[20]对CmOhpNCn型系列杂双子表面活性剂在水溶液中的自组装行为进行了考察,建立了胶束形态与分子结构、浓度、温度之间的关系.Kwasniewska等[21]则聚焦于3种新型的杂双子表面活性剂,发现疏水链长度对吸附特性和胶团寿命有显著影响,且临界胶束浓度随疏水链长度的增加而降低.针对Cn-1EC-s-Cm型杂双子表面活性剂,Yu等[22]建立了γcmc与疏水链长度的关系.
综上所述,杂双子表面活性剂由于在分子结构上具有明显的不对称性和较大的可调节性,使其自组装行为较对称型双子表面活性剂更为复杂,相应的自组装结构也更加丰富多样.因而针对此类体系的自组装行为所开展的基础性研究必将有助于从分子水平上对自组装机理有更加深入的理解与认识,并在构筑具有新颖结构的分子有序聚集体等方面发挥重要的作用[23].但就目前的情况来看,与之相关的研究工作既不全面也不深入,且大多局限于实验研究,而真正能够对其内在机理进行深入探寻并将结果以直观方式呈现出来的理论与模拟研究鲜有报道[24-26],针对杂双子表面活性剂实际体系的模拟工作更尚未见报道.为此,本工作着眼于Cm-P-N-Cn型系列杂双子表面活性剂,对其在水溶液中的自组装行为开展耗散粒子动力学(dissipative particle dynamics,DPD)模拟研究,并重点关注体系浓度与疏水链长度对其自组装行为产生的影响.
1 模拟方法与模型构造
DPD方法由Hoogerbrugge和Koelman提出[27-28],后经其他研究者多次完善[29-30],已在众多领域得到了成功应用,并被证明是一种研究复杂流体介观尺度行为的有效方法[31-33].DPD体系中的基本单元为代表实际体系分子集团的粗粒化软粒子,其时间演化遵循牛顿运动定律[30].粒子间的相互作用力fi由三部分组成,其中每一部分均通过成对加和计算得出:
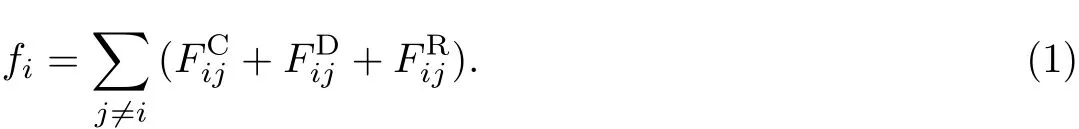
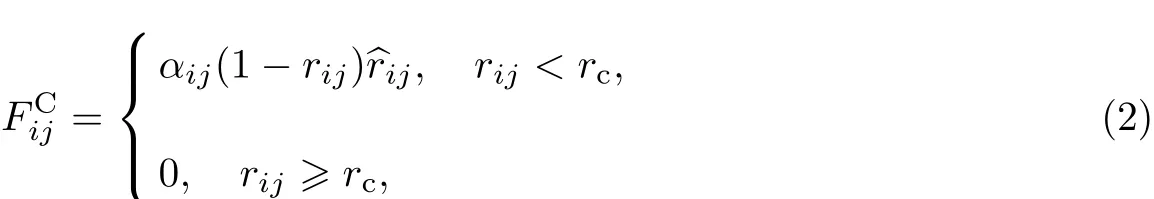
式中,αij是粒子i与粒子j之间的最大排斥力,rij=ri-rj,rij=|rij|,r^ij=rij/|rij|,rc为截断半径.耗散力正比于粒子间的相对速度,从而将能量从体系中移走.而随机力FiRj则相应地将能量注入体系,共同作用的结果是作为调温器,保证系统的(角)动量守恒以对应于正则系综的统计力学性质.之间必须满足一定的关系,可分别表示为
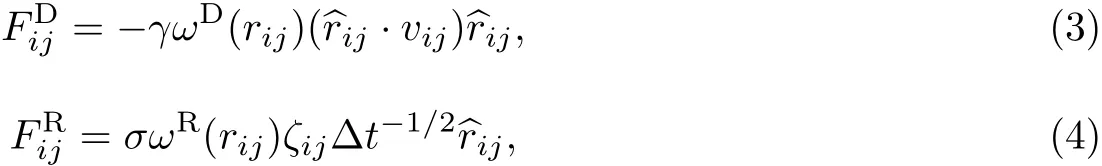
式中,ωD和ωR是与粒子间距离有关的权重函数,vij=vi-vj,ζij是随机涨落变量,满足如下条件:

Espa˜nol等[29]通过进一步研究指出,为了得到Gibbs系综的运动方程稳定解以及满足耗散涨落理论,两个权重函数ωD和ωR中的一个可以任意选取,另一个则由其决定.一个最简单的选择是:
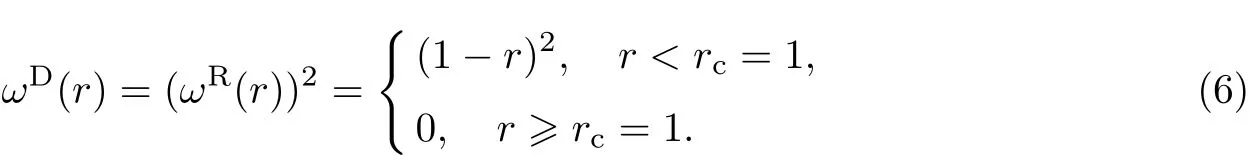
耗散力和随机力中的系数及温度之间存在以下关系:

式中,σ是随机力的标准差(或称为噪声振幅),γ是黏滞系数,也被称作摩擦因子,kB为Boltzmann因子,T为体系的绝对温度.
与其他模拟方法一样,DPD模拟中的物理量必须进行对比化处理.通常选择粒子的实际质量m和半径rc(即粒子间相互作用范围)分别作为体系的质量和长度单位,以kBT作为体系的能量单位,即m=rc=kBT=1.其他物理量均可以通过与m,rc,kBT的组合项进行对比来实现无量纲化:
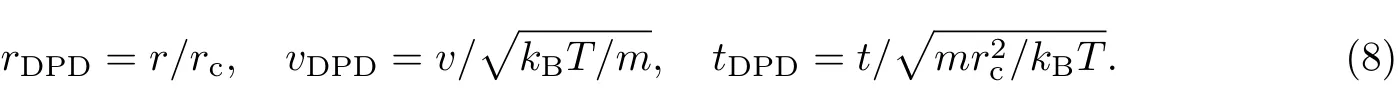
因此,单一的DPD模拟结果可以对应许多体系,这主要取决于粒子的质量、半径和温度等相关参数的取值.
本工作涉及的模拟体系中,水为溶剂,而作为溶质的杂双子表面活性剂则包括10种类型,即Cm-P-N-Cn(m,n=9,9;9,12;9,15;9,18;12,12;12,15;12,18;15,15;15,18;18,18),其分子结构和相应的DPD软粒子模型如图1所示,其中TA和TB均为3个亚甲基组合而成的疏水基团,HA为磷酸根阴离子基团,S为2个亚甲基组合而成的联接基团,HB为季铵根阳离子基团,W为水粒子.
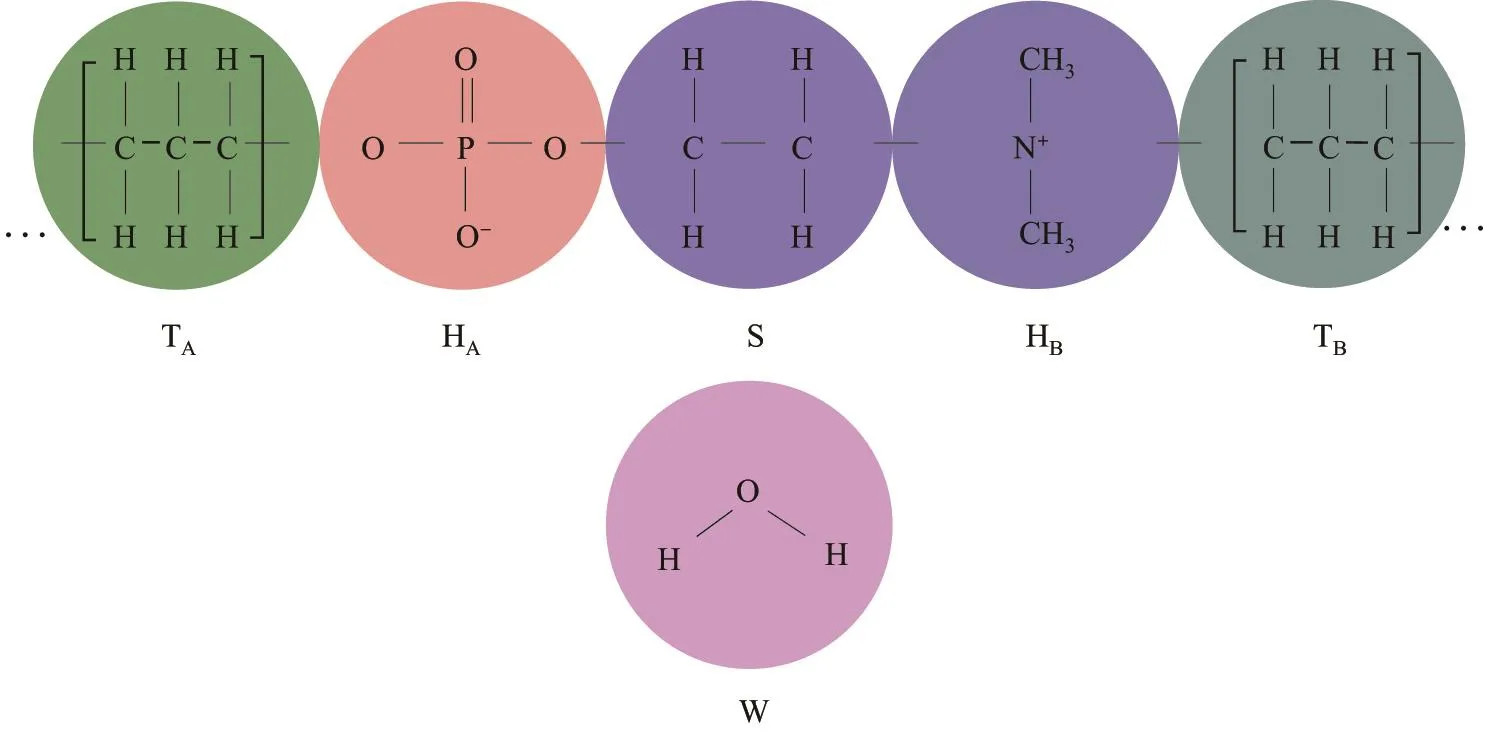
图1 杂双子表面活性剂和水的分子结构以及相应的DPD软粒子模型Fig.1 Configurations of heterogemini and water molecules together with corresponding DPD soft bead model
式(2)中的相互作用参数αij对于DPD模拟至关重要.根据著名的Flory-Huggins理论[30]可以表示为

式中,χij是粒子i与粒子j之间的溶解度参数,即

其中Emix为混合能,即两种物质由于相互混合而较纯净物状态所产生的自由能变化.在传统的Flory-Huggins模型中,各组分均占据一晶格点位.对于配位数为Z的晶格,其混合能为
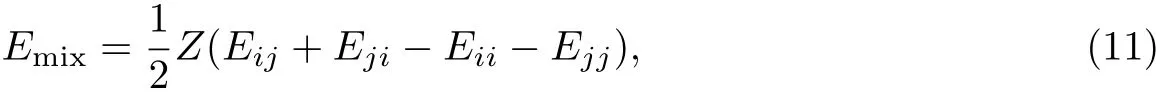
式中,Eij为单位组分i与单位组分j之间的结合能.
基于图1所示的DPD软粒子模型,相应的相互作用参数αij计算结果如表1所示.此外,键对粒子间通过简谐振动弹性力=Crij相互连接约束,其初始键长为单位长度.
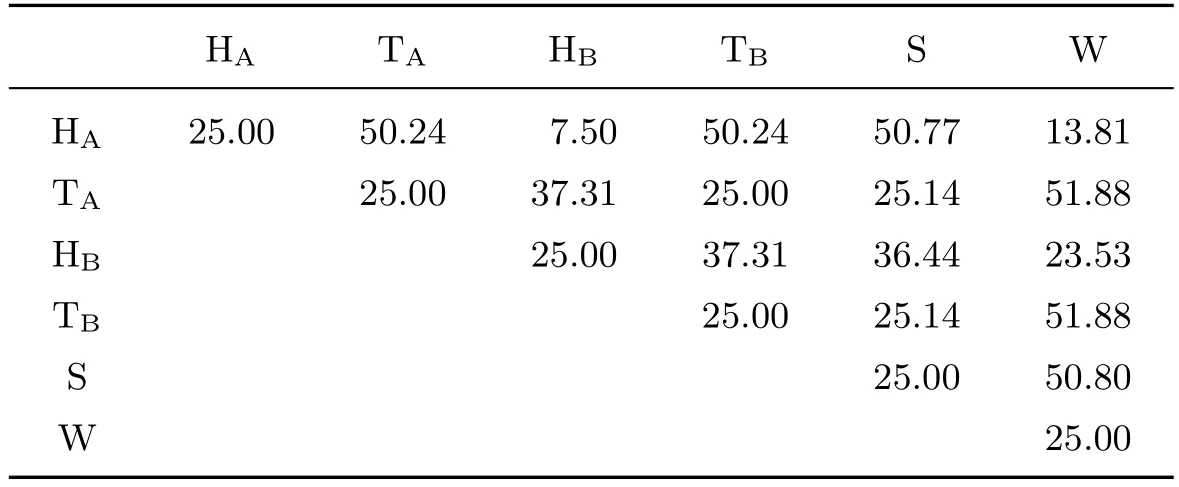
表1 DPD软粒子间相互作用参数(kBT)Table 1 Interaction parameters between DPD beads(kBT)
DPD模拟在一大小为30(x)×30(y)×30(z)r3c的立方盒子中进行,x,y和z方向均实施周期性边界条件,更大体系更长时间步的模拟表明该体系足以避免有限尺寸效应的产生.体系数密度ρ=3,随机力标准差σ=3.67,弹性系数C=100.0.数值积分采用标准Velocity-Verlet算法[30],相应的步长Δt=0.05.每一轮模拟均进行5×105时间步,其中最后的5×104步用于平衡量化信息的统计.
2 结果与讨论
2.1 确保体系平衡
作为DPD流体的特征参数之一,扩散系数被看作流体粒子扩散到一定距离所需时间与在同一距离上流体力学相互作用达到稳态所需时间的比值[30].因而,在每一轮DPD模拟中,各个粒子的扩散系数可用来检验体系平衡[35-37].根据Einstein公式[38],可通过计算每一类粒子的均方位移得到扩散系数:
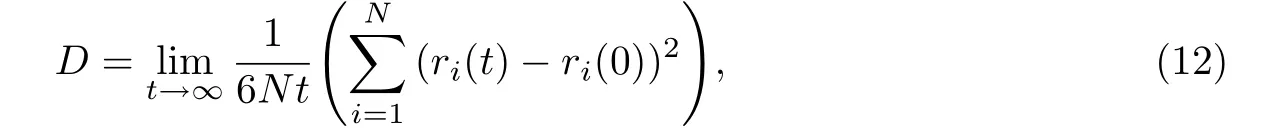
式中,N为某一类型粒子在模拟体系中的数量,t为模拟演化时间,ri(0)和ri(t)分别表示粒子i在0时刻与t时刻的位置矢量.
图2为DPD模拟所涉及最高体系浓度(杂双子表面活性剂体积分率φ=0.5)下,C9-P-NC18体系中各DPD软粒子的扩散系数(D)随模拟步数(Ns)的变化情况.显然,当模拟进行一段时间(至多5×104时间步)之后,各类粒子的扩散系数均无大的起伏,仅有小的波动,充分表明该体系已达平衡.由此可见,5×105时间步应足以确保每一轮模拟达到平衡状态.
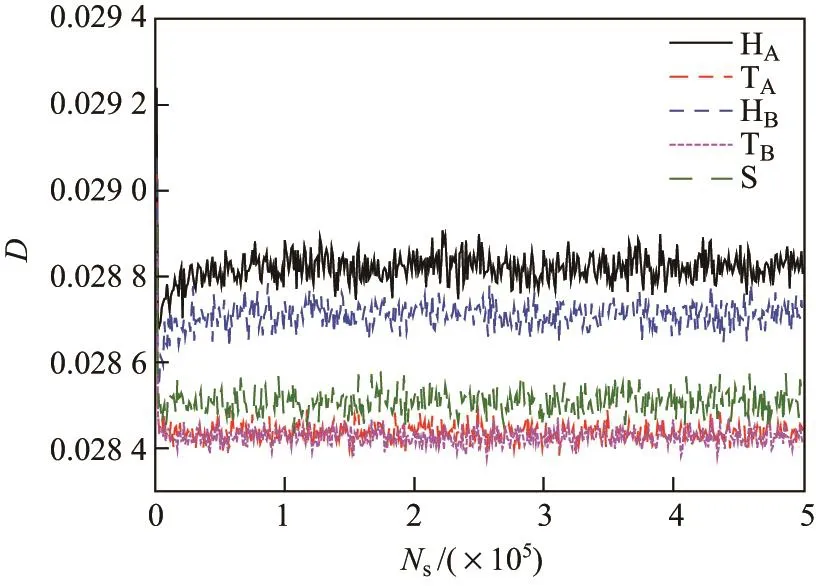
图2 C9-P-N-C18体系中DPD粒子的扩散系数与模拟步数的关系(φ=0.500)Fig.2 Evolution of the diffusion coefficient of DPD particles with the simulation step in the C9-P-N-C18system at φ=0.500
2.2 体系浓度的影响
DPD模拟所得自组装结构包括球状(sphere,S)、柱状(rod,R)、平面网格(planar grid,PG)、层状(lamella,L)、蜂窝状(honeycomb,H)、一维孔道(one-dimensional tunnel,1DT)、二维孔道(two-dimensional tunnel,2DT)和三维孔道(three-dimensional tunnel,3DT)8种(见图3).为清晰起见,作为溶剂的水未在图中显示,且每种结构均配有正视图与侧视图.水溶液中Cm-P-N-Cn的浓度(体积分率φ)对于自组装结构的影响为本工作的主要关注点,同时对疏水链不等长(m/=n)和等长(m=n)两种情况予以分别考察.图4和5则为相应的自组装相图.显然,当Cm-P-N-Cn浓度处于较低水平(φ=0.050)时,所有体系中均出现了球状胶束,这一点与传统单体、对称型双子表面活性剂体系相类似.而球状胶束进一步聚集而成的柱状胶束则出现于绝大多数体系之中.一般而言,溶液中表面活性剂浓度越高,所形成的自组装形态尺度越大.相对而言,球状与柱状分别属于小尺度和中等尺度结构,而其余结构均为大尺度结构.此类杂双子表面活性剂的自组装行为中,最为显著的特征莫过于(一维、二维和三维)孔道结构的出现并覆盖相图中至少50%的面积.体系浓度显然是三类孔道结构之间相互转化的主要控制因素之一.随着浓度φ的升高,三维孔道的部分表面与内部空间将会被不断进入溶液的表面活性剂分子逐渐填充,从而引起孔道维度的降低,二维孔道与一维孔道相继形成,而在此过程中出现的层状结构则可看作是三维孔道在某一方向降维后先于二维孔道形成的一种稳定状态.而二维孔道的形成又可以理解为当层状结构处于饱和状态后,持续加入溶液的表面活性剂分子无法融入其中,只能在外部聚集,最终将其相互连接.为了有更为全面的了解,本工作在更多的体系浓度下进行了模拟,结果显示,C9-P-N-C12体系于φ=0.085和0.325时分别形成了柱状和二维孔道结构,C9-P-N-C18体系于φ=0.285时形成了层状结构,C12-P-N-C15体系于φ=0.075时形成了柱状结构,C12-P-N-C18体系于φ=0.325时形成了层状结构.由此可见,所有模拟体系均随杂双子表面活性剂浓度的逐步升高而呈现出“球状—柱状—平面网格—三维孔道—层状—二维孔道—一维孔道”的结构转化规律.而作为一种新颖的自组装形态,于φ=0.500时出现在C9-P-N-C9和C9-P-N-C15两个体系中的蜂窝状结构则可以理解为持续加入的表面活性剂分子将一维孔道部分堵塞所致.

图3 DPD模拟所得Cm-P-N-Cn型杂双子表面活性剂在水溶液中形成的自组装结构Fig.3 DPD simulated self-assembly morphologies of Cm-P-N-Cnheterogemini surfactant in aqueous solution
2.3 疏水链长度的影响
已有多项研究[12-18]表明,杂双子表面活性剂分子的疏水链长度对其自组装行为有显著影响,而这一点也在前述内容中得以体现,尤以Cm-P-N-Cn分子中两根疏水链不等长(m/=n)时的情况最为明显.当φ=0.100时,C9-P-N-C12体系形成平面网格结构,而C9-P-N-C15,C9-P-N-C18两个体系却形成柱状结构,C12-P-N-C15和C12-P-N-C18体系分别形成平面网格与柱状结构.这一现象可归因于杂双子表面活性剂分子本身的拓扑结构与其所形成的自组装形态间弯曲(不对称)程度的一致性,即不对称性越高的分子更有利于弯曲程度越大的结构形成.类似的情况出现于多个浓度条件下,例如,当φ=0.250时,三维孔道结构出现于C9-P-N-C18和C12-P-N-C18体系之中,而其他体系则形成层状结构;当φ=0.300时,若Cm-P-N-Cn分子其中一根疏水链的长度达到或超过另一根的1.5倍,则二维孔道结构取代层状结构成为最终的自组装结构.与此同时,当φ=0.350,0.400时,二维孔道结构出现于不对称性较高的Cm-P-N-Cn体系中.而当φ=0.050,0.150,0.200和0.450时,疏水链长度对自组装行为无影响,此范围覆盖相图(见图4)40%的区域.
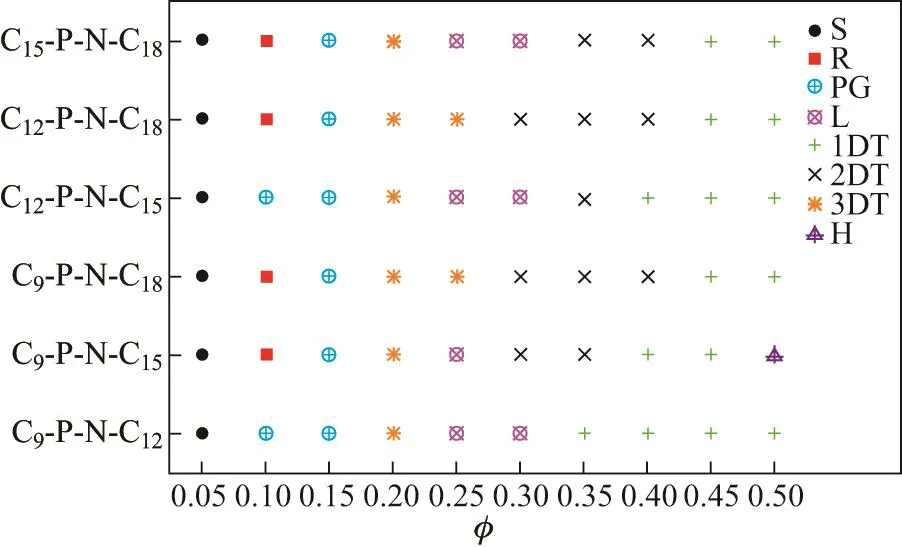
图4 疏水链不等长(m/=n)时Cm-P-N-Cn型杂双子表面活性剂在水溶液中的自组装相图Fig.4 Phase diagram for the self-assembly morphologies of Cm-P-N-Cnheterogemini surfactant in aqueous solution when m/=n
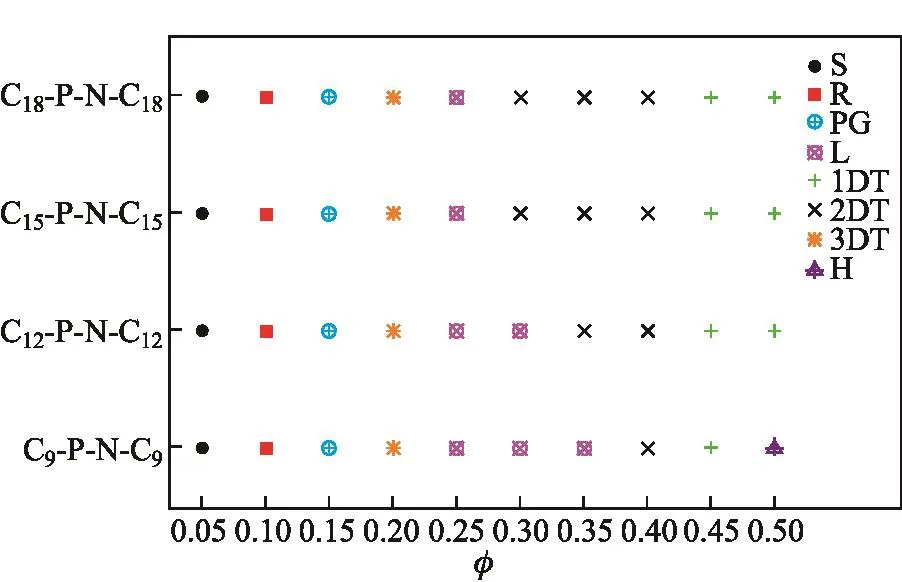
图5 疏水链等长(m=n)时Cm-P-N-Cn型杂双子表面活性剂在水溶液中的自组装相图Fig.5 Phase diagram for the self-assembly morphologies of Cm-P-N-Cnheterogemini surfactant in aqueous solution when m=n
与疏水链不等长的情况相比,当Cm-P-N-Cn分子中的两根疏水链长度相等(m=n)时,其链长对于自组装行为的影响较小.除前面提及的蜂窝状结构(φ=0.500)之外,疏水链长度仅在两个浓度下对自组装行为有影响.而这一点可完全归因于此时的Cm-P-N-Cn分子有着近乎对称的拓扑结构.众所周知,层状胶束的形成源于表面活性剂分子以“一对一”方式自组装而成的具有一定厚度的“大平层”,其表面主要由亲水头基组成,内部则由排列较为整齐的众多疏水尾链所构成.在一定体系浓度下,表面活性剂分子的尾链越长,整齐排列形成层状结构的难度就越高.因此,当φ=0.300,0.350时,疏水链长度的增加促使层状结构转变为二维孔道结构.而在其余体系浓度下,疏水链长度对自组装行为无影响,此范围覆盖相图(见图5)70%的区域.
2.4 深入分析
径向分布函数g(r)是微观结构定量化表征的重要手段之一,g(r)直接给出了距参考粒子r处发现其他粒子的概率.图6反映了C9-P-N-C15水溶液中各个亲(疏)水基团(HA,HB,TA,TB)与水分子间的相互作用强弱.前述8种自组装结构在该体系中相继出现,故其具有相应的代表性.从图中可以看出,随着溶液中表面活性剂浓度的不断升高,亲水和疏水基团周围均会有更多的水分子出现,其主要原因在于,Cm-P-N-Cn分子中的离子头基与极性水分子间存在相互吸引,且体系浓度越高,Cm-P-N-Cn分子与水分子的接触机会越多,因而在任一Cm-P-N-Cn分子附近出现水分子的概率就越大.显然,图6(a)中各峰的强度远超图6(b),说明相较于HB,HA对于水分子的吸引力更大,而这一点恰与实际情况以及人们对此类基团的普遍认识相符.对于同样由3个亚甲基构成的疏水基团TA和TB,出现在其周围的水分子要少得多,因而图6(c),(d)中未有明显的峰形出现,且两组曲线间无显著差别.在选取低(φ=0.100)、中(φ=0.300)、高(φ=0.500)浓度的基础上,图7和8分别体现了疏水链不等长(m/=n)与等长(m=n)两种情况下各个Cm-P-N-Cn分子中的HA与水分子间的亲近程度.Cm-P-N-Cn分子的疏水链越长,其疏水性越强,在一定浓度下更为倾向于相互聚集.因此,Cm-P-N-Cn分子在所形成自组装结构内部的排列更为紧密,其表面“覆盖”的亲水基团密度更高,能够对溶液中的水分子产生更为强大的吸引力,促使更多的水分子分布于离子头基附近.而体系浓度的作用依旧与图6中相同.此外,疏水链总长度相同的C9-P-N-C18分子和C12-P-N-C15分子所在体系之间的区别值得关注.众所周知,杂双子表面活性剂的优势主要缘于其分子在拓扑结构上的不对称性.相比之下,C9-P-N-C18的优势更为明显,能够在一定浓度的水溶液中形成内部排列更加紧密的自组装结构,富集于其表面的离子头基也就会被更多的水分子所围绕.
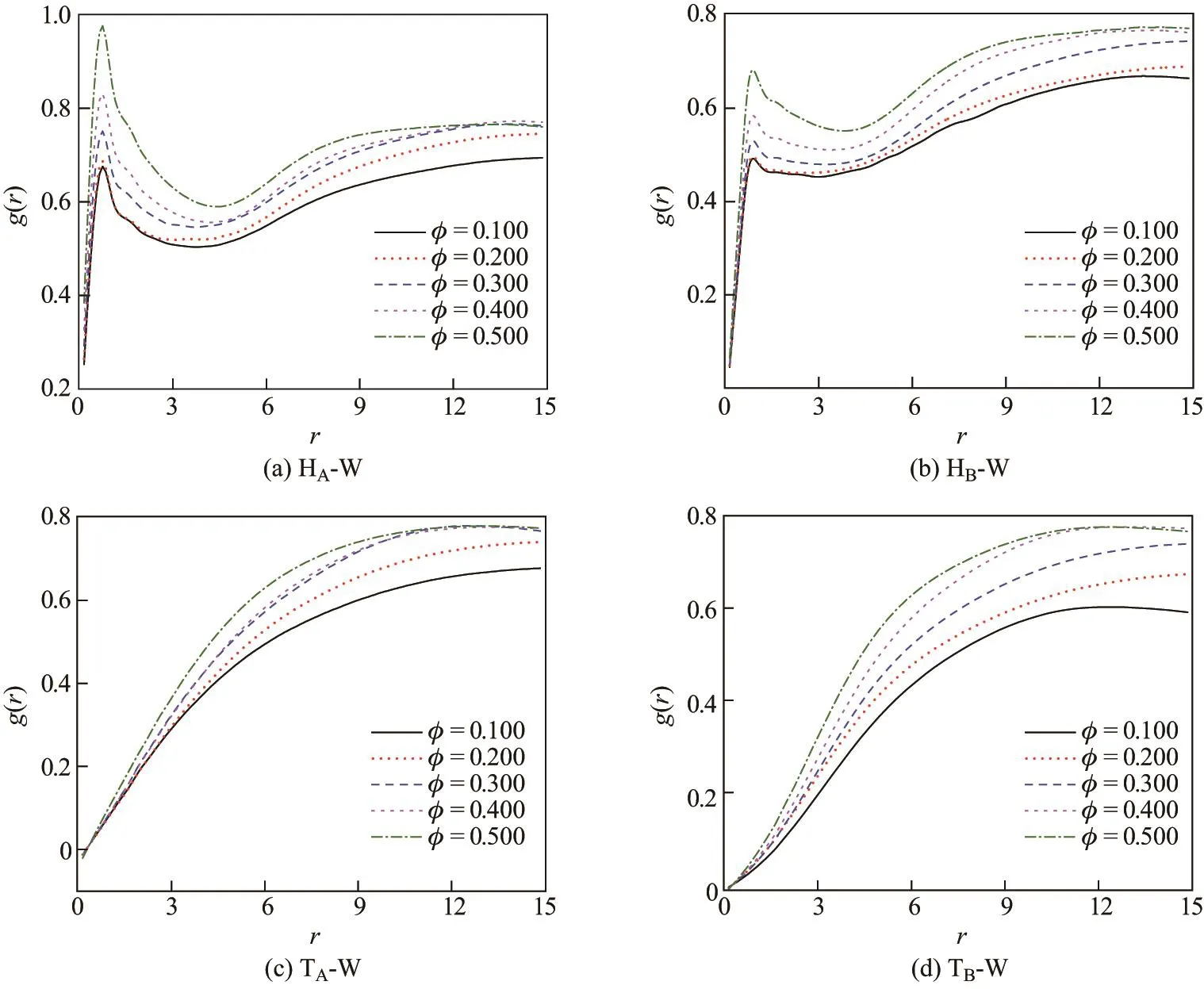
图6 C9-P-N-C15分子水溶液中亲(疏)水基团(HA,HB,TA,TB)与水粒子(W)间的径向分布函数g(r)Fig.6 Radial distribution function g(r)between hydrophilic and hydrophobic groups(HA,HB,TA,TB)in the C9-P-N-C15molecule and water(W)in corresponding aqueous solution
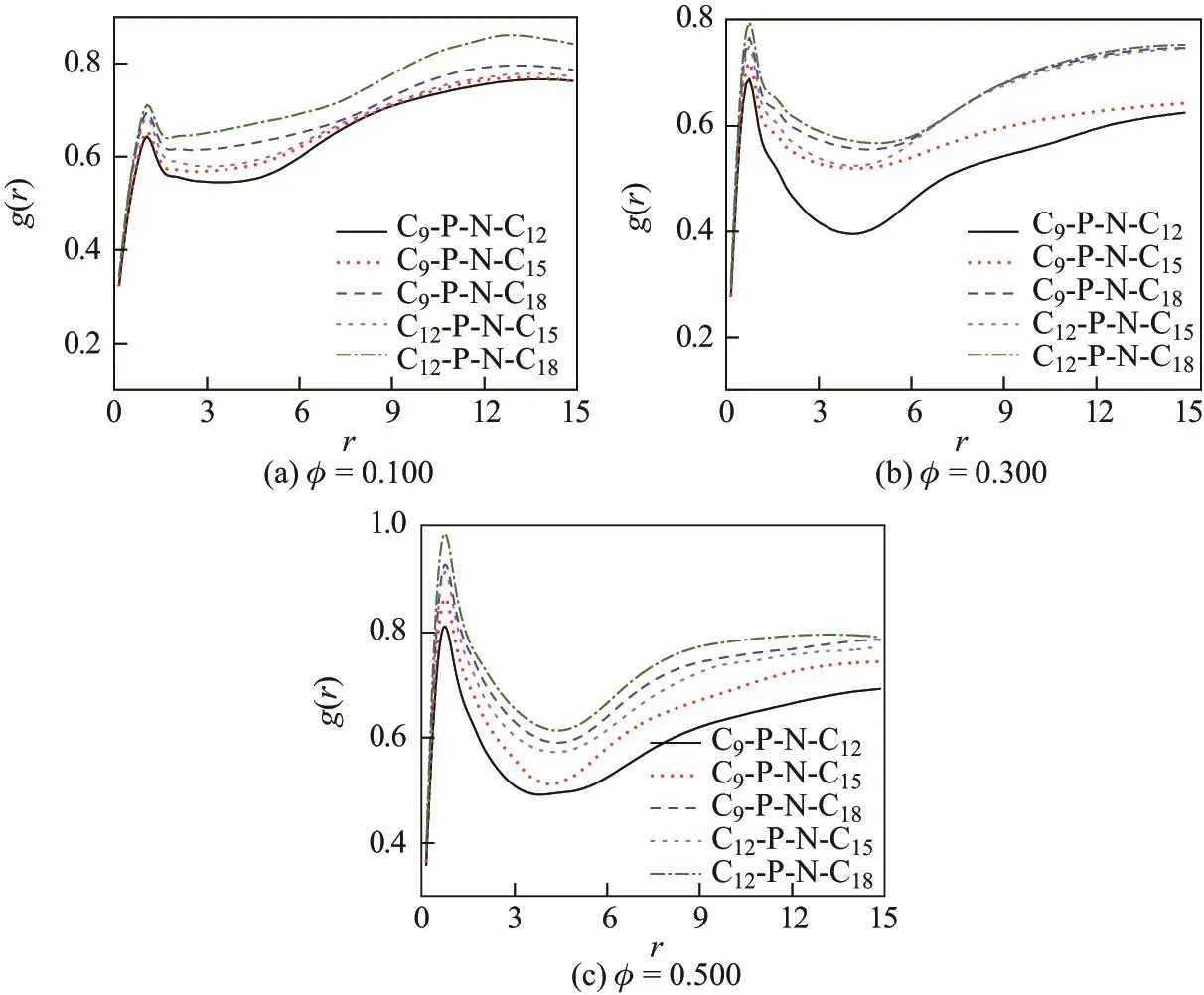
图7 体系浓度φ=0.100,0.300和0.500时疏水链不等长(m/=n)的Cm-P-N-Cn分子水溶液中HA与W间的径向分布函数g(r)Fig.7 Radial distribution function g(r)between HAand W in Cm-P-N-Cnmolecule system when m/=n at concentrations of φ=0.100,0.300 and 0.500
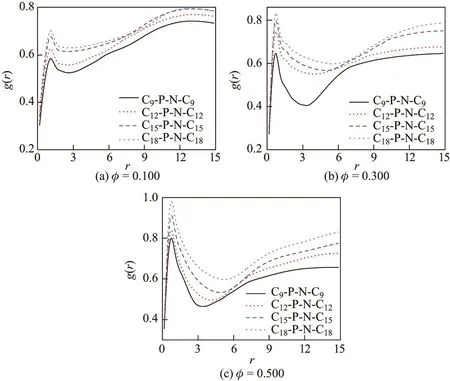
图8 体系浓度φ=0.100,0.300和0.500时疏水链等长(m=n)的Cm-P-N-Cn分子水溶液中HA与W间的径向分布函数g(r)Fig.8 Radial distribution function g(r)between HAand W in Cm-P-N-Cnmolecule system when m=n at concentrations of φ=0.100,0.300 and 0.500
3 结束语
本工作利用耗散粒子动力学方法对Cm-P-N-Cn(m,n=9,9;9,12;9,15;9,18;12,12;12,15;12,18;15,15;15,18;18,18)型系列两性杂双子表面活性剂在水溶液中的自组装行为开展了模拟研究,观察到了球状、柱状、平面网格、层状、蜂窝状、一维孔道、二维孔道和三维孔道多种自组装结构的形成.所有模拟体系均随表面活性剂浓度的逐步升高而呈现出“球状—柱状—平面网格—三维孔道—层状—二维孔道—一维孔道”的结构转化规律.当m/=n时,疏水链长度对于自组装行为有显著影响.此外,径向分布函数可完全体现Cm-P-N-Cn分子内部各功能基团与水分子间的相互作用强弱和亲近程度.模拟结果可为今后针对此类体系的进一步研究提供相应的理论帮助与指导.

