纤维增强复合材料加固裂纹黏弹性梁的弯曲变形

杨 骁,成博炜,蒋志云

(上海大学土木工程系,上海200444)

由于初始缺陷或环境的作用,作为结构主要构件的梁——钢筋混凝土梁或木梁等在服役期会不可避免地产生性能退化,并出现各类裂纹.裂纹尖端的应力集中及疲劳往往导致裂纹扩展,使梁刚度和承载能力降低,最终发生破坏,对生命和财产造成严重威胁,因此裂纹梁的加固与修复成为相关研究领域的关注课题.

针对梁的黏弹性,陈云鹤等[1]试验研究了钢筋混凝土梁的蠕变,采用标准线性固体模型,给出了钢筋混凝土的应力-应变曲线及其黏弹性参数;孟江等[2]分别采用ACI(American Concrete Institute,美国混凝土协会)模型、BP(back propagation,反向传播)模型、CEB-FIP(Comit´e Euro-International du B´eton-F´ed´eration Internationale de la Pr´econtrainte, 欧洲混凝土委员会-国际预应力协会)模型和GL-2000模型(美国混凝土徐变模型)等,研究了混凝土加载龄期和环境湿度等对钢筋混凝土梁收缩徐变的影响;Hamed[3]建立了受压混凝土的非线性蠕变模型,研究了钢筋混凝土梁的非线性蠕变特性,并试验验证了该模型的可靠性与准确性;Fan等[4]试验研究了混凝土的动蠕变特性,而Hedegaard等[5]基于有限元模型,假定混凝土服从黏弹性Kelvin链本构模型,建立了钢筋混凝土及预应力钢筋混凝土的数值模拟方法.Fridley等[6]对花旗松(Douglas-fir,DF)的蠕变进行了大量试验研究,揭示了DF木材的蠕变机理,并给出Fridley幂律蠕变模型的材料参数;陈晓艳等[7]对杨木梁进行了三点弯曲试验,给出了其黏弹性Burger模型的材料参数;Hassani[8]考虑含水率的影响,给出了木材正交各向异性黏弹塑性本构模型,并通过有限元模拟与试验结果对比,验证了该本构模型的合理性.

纤维增强复合材料(fiber reinforced polymer,FRP)以其优异的力学性能、良好的黏合性和耐久性已广泛应用于混凝土结构、钢结构和木结构等的加固修复[9-13].Plevris等[14-15]考虑混凝土水热效应和FRP黏性性质,基于Findley幂律模型,分别研究了FRP加固混凝土梁和木梁的蠕变行为;Diab等[16]研究了界面黏性对FRP加固混凝土梁的影响;Gonilha等[17]研究了玻璃纤维增强复合材料(glass fiber reinforced polymer,GFRP)-混凝土组合梁的蠕变响应;而Berardi等[18]研究了轴力作用下FRP筋混凝土梁的长期蠕变效应;Davids等[19]试验研究了FRP加固层合木梁的弯曲蠕变行为,给出了弯曲蠕变计算方法.基于黏弹性材料的Findley幂律模型,Yahyaei-Moayyed等[20-21]试验研究了GFRP和芳纶纤维增强复合材料(Aramid fiber reinforced polymer,AFRP)分别加固南美黄松(southern yellow pine,SYP)和花旗松(DF)梁的蠕变行为,得到木材材料参数;陆伟东等[22]采用黏弹性四参数Burger模型拟合了FRP板增强胶合木梁的应力-应变关系,并分析了破坏机理;Pulngern等[23]利用有限元法研究了黏弹性Findley幂律模型的木-聚氯乙烯(polyvinyl chloride,PVC)组合构件短期性能和长期蠕变行为.由于缺少木材的严格黏弹性本构参数,且为避免数学处理难度,目前对于FRP加固木梁黏弹性行为的研究主要基于Findley幂律模型,为此欧阳煜等[24]基于已有试验数据,给出了南美黄松(SYP)和花旗松(DF)的黏弹性标准线性固体本构参数,并建立了FRP加固黏弹性Euler-Bernoulli木梁弯曲控制方程,研究了突加均布载荷作用下AFRP布加固简支和固支DF木梁的弯曲蠕变.

Wu等[25-26]研究了FRP加固裂纹混凝土梁的承载力,并且考虑混凝土梁横向裂纹传播和FRP界面剥离扩展,给出了FRP加固裂纹混凝土梁弯曲变形的解析解;Hmidan等[27]利用有限元模拟了FRP加固钢梁的裂纹传播和FRP界面剥离;Triantafillou[28],Svecova等[29],Akbiyik等[30]以及G´omez等[31]研究了FRP加固纵向裂纹木梁的抗剪和抗弯性能,指出FRP加固可明显提高木梁抗剪和抗弯刚度.然而,有关FRP布加固裂纹黏弹性梁弯曲的研究尚未见报道,若干问题有待深入探究.

本工作研究底部粘贴FRP布加固简支横向裂纹黏弹性梁的弯曲蠕变.假定FRP布与梁底部紧密粘贴,考虑裂纹缝隙效应,利用裂纹的等效旋转弹簧模型,首先给出FRP布加固裂纹梁的裂纹等效旋转弹簧刚度;其次,根据FRP布加固黏弹性梁弯曲变形的控制方程和梁弯曲的边界条件以及考虑裂纹闭合效应的裂纹处连接条件,利用Laplace变换及其逆变换,得到突加均布载荷作用下FRP布加固简支裂纹黏弹性梁弯曲蠕变的解析解;最后,数值考察了裂纹位于梁上表面或下表面时,碳纤维增强复合材料(carbon fiber reinforced polymer,CFRP)布含量、梁跨高比和裂纹开闭状态等对CFRP布加固裂纹花旗松(DF)木梁的弯曲蠕变影响.

1 FRP布加固裂纹黏弹性矩形截面梁弯曲变形的控制方程

如图1所示,设长为L、宽和高分别为b和hⅠ、在x=x0处的深度和初始张开角分别为d0和θ0的横向裂纹简支黏弹性梁在载荷Q(x,t)的作用下发生弯曲.记梁拉伸松弛模量为Y(t),横截面面积和形心主惯轴惯性矩分别为AⅠ和IⅠ,且形心到梁底部的距离为rⅠ.为提高梁的刚度和承载力,在其下表面粘贴FRP布进行加固,FRP布的弹性模量为EⅡ,宽和厚分别为b和hⅡ(hⅡ≪hⅠ),横截面面积为AⅡ.假定FRP布加固裂纹黏弹性梁的变形满足:

(1)梁为服从标准线性固体本构的黏弹性体(见图2),FRP布为弹性体,且变形为小挠度、小应变;

(2)梁满足Euler-Bernoulli梁弯曲变形假定,且仅考虑FRP布的拉伸变形,忽略其弯曲效应;

(3)梁下表面与FRP布紧密粘贴,二者间无掀起和滑移.

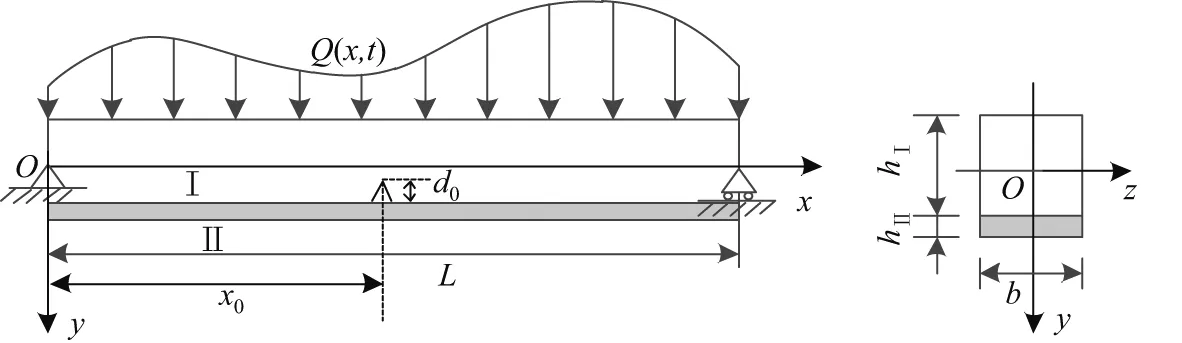
图1 FRP布加固裂纹黏弹性梁的几何尺寸Fig.1 Geometric parameters of cracked viscoelastic beam reinforced with FRP sheet

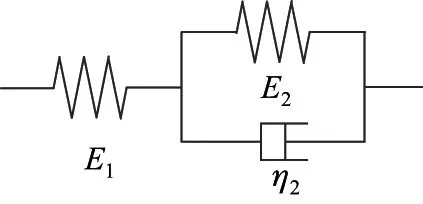
图2 黏弹性标准线性固体本构物理模型Fig.2 Physical model of the standard linear solid constitutive relation of viscoelasticity

若梁为服从标准线性固体本构的黏弹性体[32],则松弛模量Y(t)可表为

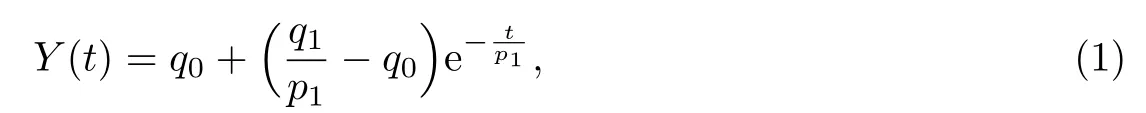
式中,参数p1,q0和q1与图2所示黏弹性标准线性固体本构物理模型中弹性和黏性元件参数的关系如下:

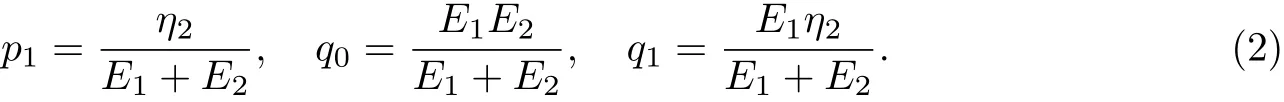
将x=x0处裂纹等效为连接于梁形心处刚度为K0的旋转弹簧[33-35].考虑裂纹缝隙效应,当旋转弹簧向裂纹闭合方向转动角度θ0后,裂纹闭合,弹簧效应消失,即裂纹不存在.注意到,采用FRP布加固梁的同时也对裂纹进行了加固,将裂纹处的FRP布等效为拉伸弹簧,则当裂纹未闭合时,FRP布和裂纹等效旋转弹簧构成如图3所示的组合弹簧.此时,若裂纹等效旋转弹簧转动角度θ,则FRP布加固层的伸长为ΔⅡ=-θrⅠ,其相应的正应变εⅡ和拉力Ff分别为

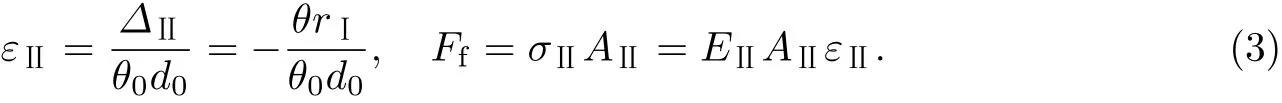
而梁裂纹等效旋转弹簧的力偶为

从而,FRP布加固裂纹后组合弹簧所受合力偶为

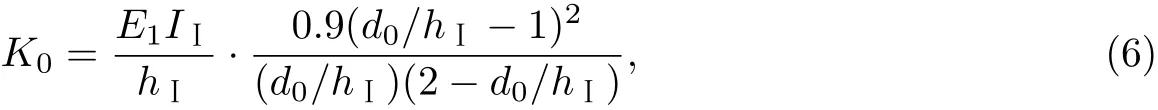
式中,E1为梁的瞬时弹性模量,即忽略梁黏性性质时的弹性模量.

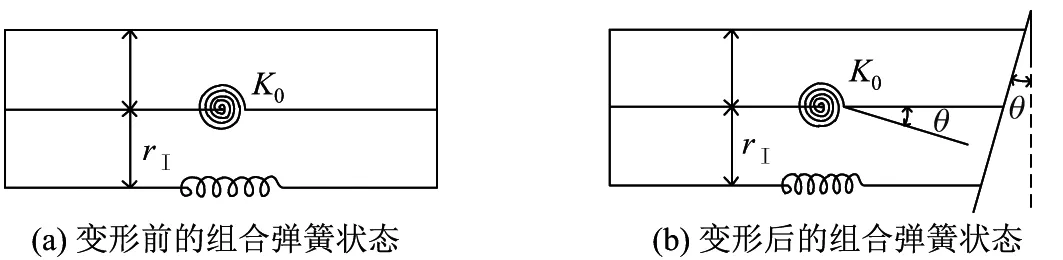
图3 FRP布加固裂纹的等效旋转弹簧模型Fig.3 Equivalent rotation spring model of FRP sheet-reinforced crack

以x=x0处裂纹为界,将FRP布加固裂纹黏弹性梁分为子梁1和子梁2,记子梁1和子梁2的轴向位移分别为u1(x,t)和u2(x,t),横向挠度分别为w1(x,t)和w2(x,t),则子梁1和子梁2的弯曲变形控制方程(i=1,2)[24]为

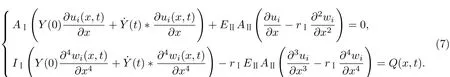
假定初始时FRP布加固裂纹黏弹性梁未变形,则其初始条件和简支边界条件分别为

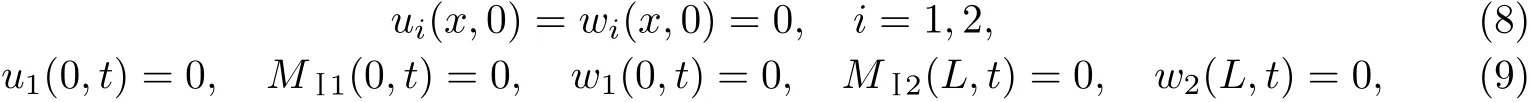
式中,MⅠi为梁横截面上的弯矩[25],且

在裂纹x=x0处,梁弯曲的连接条件要求梁轴向位移、横向挠度、横截面弯矩和剪力连续,即

式中,FSⅠi为梁横截面上的剪力[25],且

当裂纹张开时,裂纹左右两端梁横截面转角的差值,即裂纹等效旋转弹簧的转角应与梁横截面弯矩成正比;而当裂纹闭合时,裂纹左右两端梁横截面转角的差值应等于裂纹初始张开角θ0.于是,对于x=x0处的上表面裂纹,梁转角连接条件为

式中,H(x)为Heaviside函数,M(x,t)=MⅠ1(x,t)+FNⅡ1(x,t)rⅠ为FRP布加固裂纹梁的横截面弯矩,M0=K0eθ0为FRP布加固后裂纹的闭合临界弯矩,FNⅡi(x,t)为FRP布截面上的轴力[25],且

而对于x=x0处的下表面裂纹,梁转角连接条件为

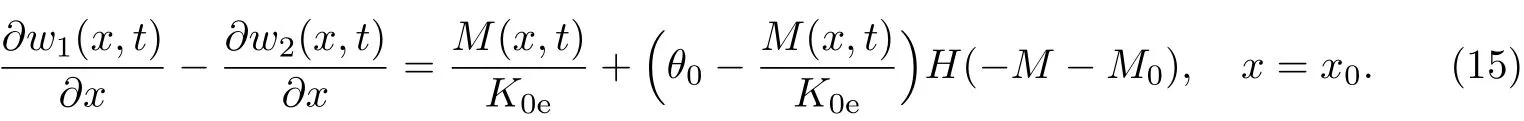
这样,控制方程式(7)、初始条件式(8)、边界条件式(9)和连接条件式(11)以及式(13)或(15)构成FRP布加固简支裂纹黏弹性梁弯曲变形的初边值问题.

2 FRP布加固简支裂纹黏弹性梁的弯曲变形解析解

假定黏弹性梁在x=x0处存在上表面裂纹,则对初边值问题式(7)～(9),式(11)和(13)关于时间t进行Laplace变换,可得

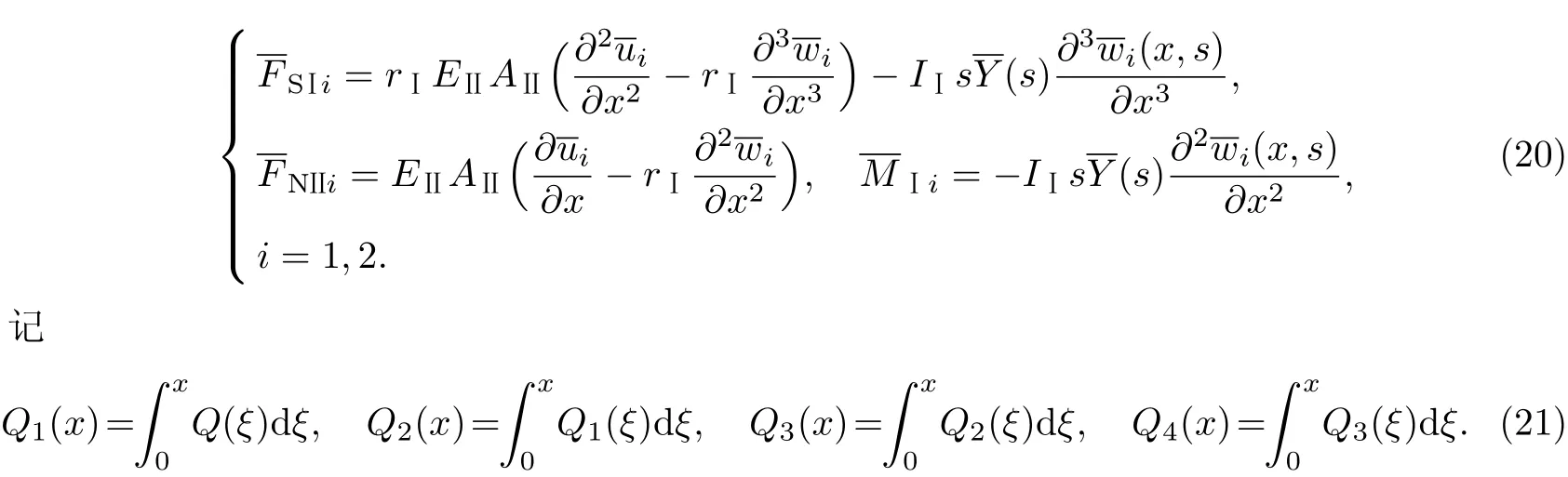
则方程式(16)的通解为

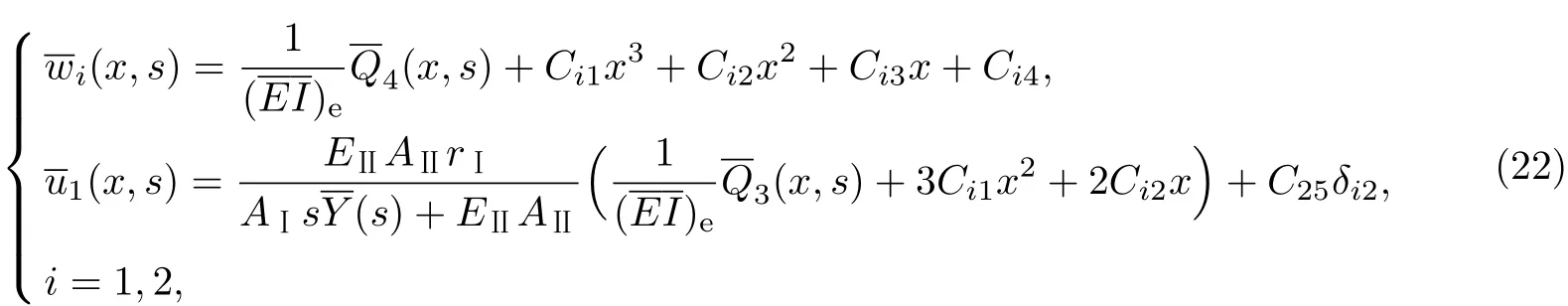
式中,δij为克罗内克符号,(EI)e为FRP布加固黏弹性梁在Laplace变换域中的等效抗弯刚度,且

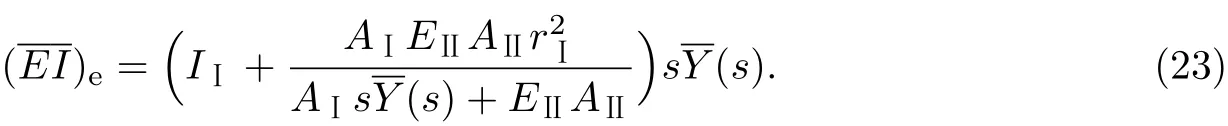
将式(22)代入边界条件式(17)后4式和连接条件式(18)可得确定待定系数C11,C12,C13,C14和C21,C22,C23,C24,C25的线性方程组,由此求得

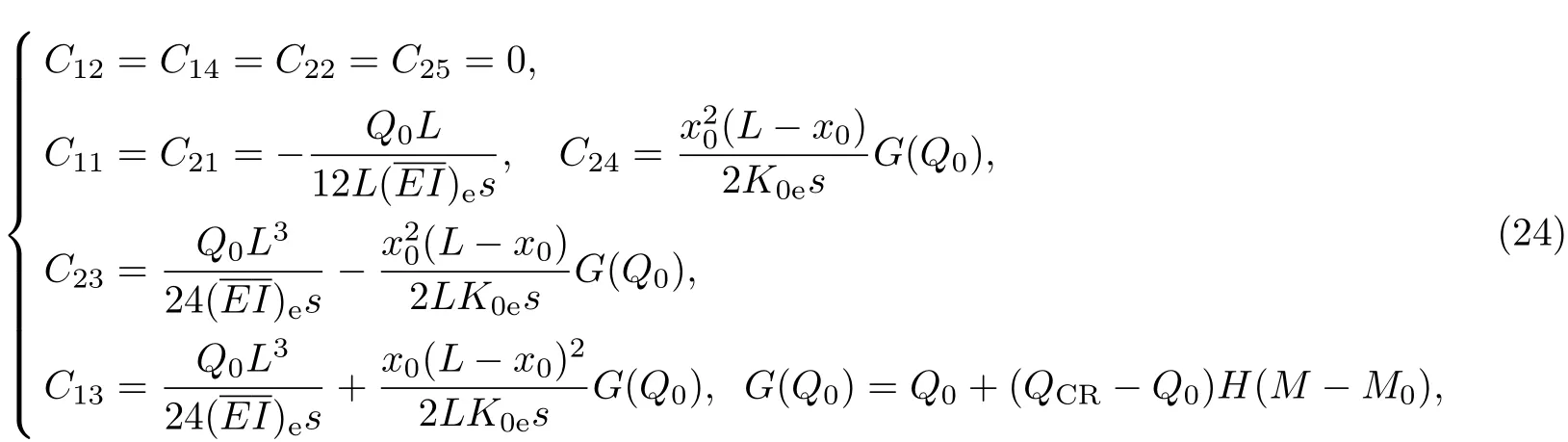
式中,QCR为裂纹闭合临界载荷,且

将式(24)代入式(22),并对其进行Laplace逆变换,可得

式中,

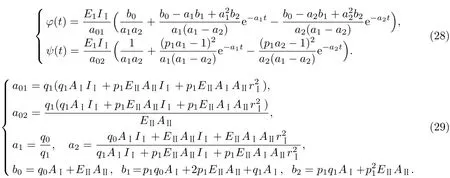
同理,假定x=x0处存在下表面裂纹,式(22)中的待定系数为

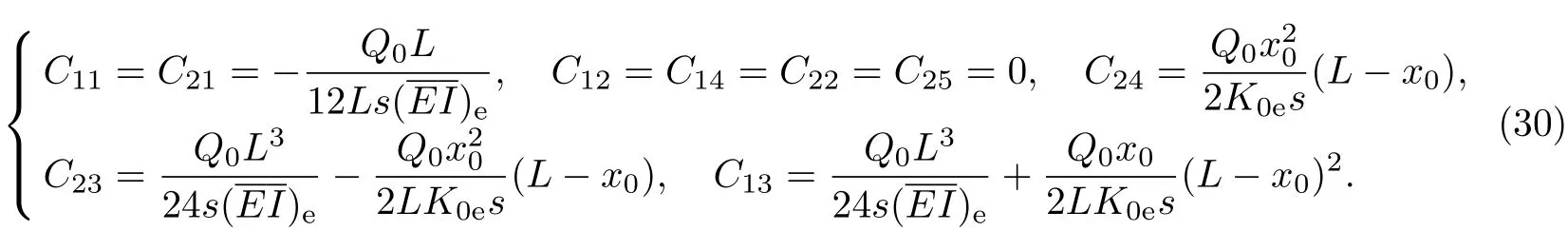
而式(26)和(27)变为

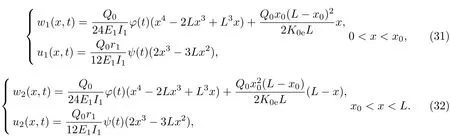
3 FRP布加固简支裂纹黏弹性木梁的弯曲蠕变

3.1 下表面裂纹梁

下面分析突加均布载荷作用下FRP布加固简支裂纹花旗松(DF)梁的弯曲蠕变.取DF梁标准线性固体本构的材料参数[6,20,24]为E1=247.72 GPa,E2=42.62 GPa,η2=11.60×103GPa·h,木梁横截面尺寸hⅠ=b=0.1 m,且在x=x0=L/2处存在深度为d0=hⅠ/2、初始角度为θ0=1°的下表面裂纹,FRP加固层为CFRP布,其弹性模量EⅡ=315 GPa[9,13,15,27].定义加固DF梁CFRP含量为H2=hⅡ/(hⅡ+hⅠ),即CFRP布加固DF梁横截面中CFRP布的面积占横截面总面积的百分数.取载荷Q0=1×106N·m-1,且定义无量纲载荷Q∗=Q0L3/(E1IⅠ).

取梁跨高比L/hⅠ=10,则无量纲载荷q=Q∗=0.484 4.图4给出了当ξ0=x0/L=0.5,d0/hⅠ=0.5时,不同CFRP加固含量H2下,CFRP布加固简支裂纹/无裂纹完整DF梁(即d0/hⅠ=0)的无量纲跨中挠度W(0.5,t∗)=w(L/2,t)/L随无量纲时间t∗=t/T的响应,其中虚线和实线分别为无裂纹完整DF梁和裂纹DF梁的挠度,T为单位时间,由于黏滞系数η2的单位取为GPa·h,故取T=1 h.可见,对于完整DF梁和裂纹DF梁及其CFRP布加固梁,跨中挠度W(0.5,t∗)均随无量纲时间t∗增加而增大,并最终趋于定值.随着加固含量H2的增加,CFRP布加固完整DF梁和裂纹DF梁的无量纲跨中挠度W(0.5,t∗)均减小,且含量H2=2.91%的CFRP布加固裂纹DF梁和CFRP布加固完整DF梁的跨中挠度基本重合,此时CFRP布的加固导致裂纹效应几乎消失.

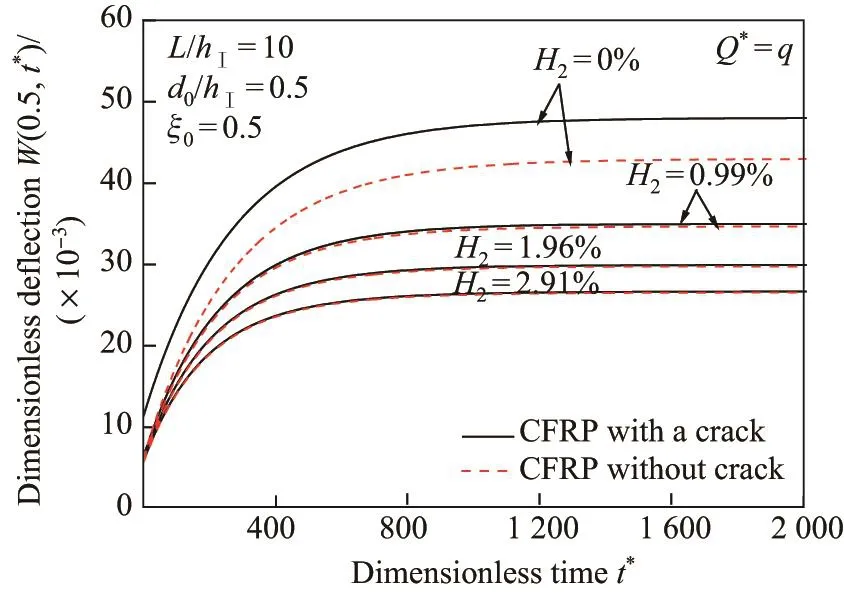
图4 CFRP布加固裂纹/完整DF梁无量纲跨中挠度W(0.5,t∗)随无量纲时间t∗的响应Fig.4 Responses of dimensionless mid-span deflections W(0.5,t∗)vs.dimensionless time t∗of CFRP sheet-reinforced cracked/intact DF beam

图5 给出了当t∗=0和2 000时,未加固(即H2=0%)和H2=2.91%的CFRP布加固完整/裂纹DF梁无量纲挠度W(ξ,t∗)=w(x,t)/L沿梁无量纲轴线ξ=x/L的分布,其中虚线和实线分别为CFRP布加固DF梁和未加固DF梁的挠度分布.可见,由于受裂纹影响,未加固和CFRP布加固裂纹DF梁的无量纲挠度大于完整DF梁挠度,且裂纹梁挠度分布在裂纹ξ0=0.5处呈现尖点.另外,当CFRP布加固含量H2=2.91%时,裂纹对DF裂纹梁的W(ξ,t∗)影响较小.当t∗=0时,未加固裂纹DF梁无量纲挠度比未加固完整DF梁无量纲挠度增加了80.00%,即裂纹对DF梁的变形影响较大;而当加固H2=2.91%的CFRP布时,裂纹DF梁无量纲挠度比未加固裂纹DF梁无量纲挠度减少了48.96%;当t∗=2 000时,这两个挠度变化值(80.00%和48.96%)分别为11.75%,44.45%,即CFRP布加固可降低裂纹效应,有效减小DF梁的挠度.

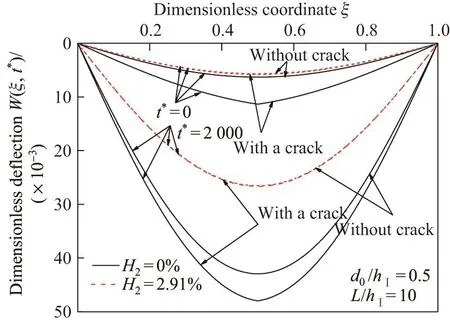
图5 未加固裂纹/完整DF梁与H2=2.91%时CFRP布加固完整/裂纹DF梁无量纲挠度W(ξ,t∗)的分布Fig.5 Distributions of dimensionless deflections W(ξ,t∗)of unreinforced and H2=2.91%CFRP sheet-reinforced cracked/intact DF beam

改变无量纲载荷Q∗,其他参数保持不变,图6给出了不同无量纲载荷Q∗和无量纲时刻t∗下,裂纹DF梁的无量纲挠度W(ξ,t∗)沿轴线ξ的分布.可见,随着载荷的增加,DF梁无量纲挠度增大.当t∗=0时,H2=2.91%的CFRP布加固裂纹DF梁比未加固裂纹DF梁的无量纲挠度减少48.96%,且此值不依赖于载荷Q∗;当t∗=2 000时,H2=2.91%的CFRP布加固裂纹DF梁比未加固裂纹DF梁的无量纲挠度减少44.45%.同时,未加固裂纹DF梁无量纲挠度曲线在裂纹ξ0=0.5处呈现尖点,而当CFRP布加固含量H2达到2.91%时,CFRP布加固DF裂纹梁的无量纲挠度W(ξ,t∗)在跨中未呈现明显尖点,这说明FRP可缓解裂纹效应,且当FRP含量达到一定值时,FRP加固可基本消除裂纹对DF梁变形的影响.

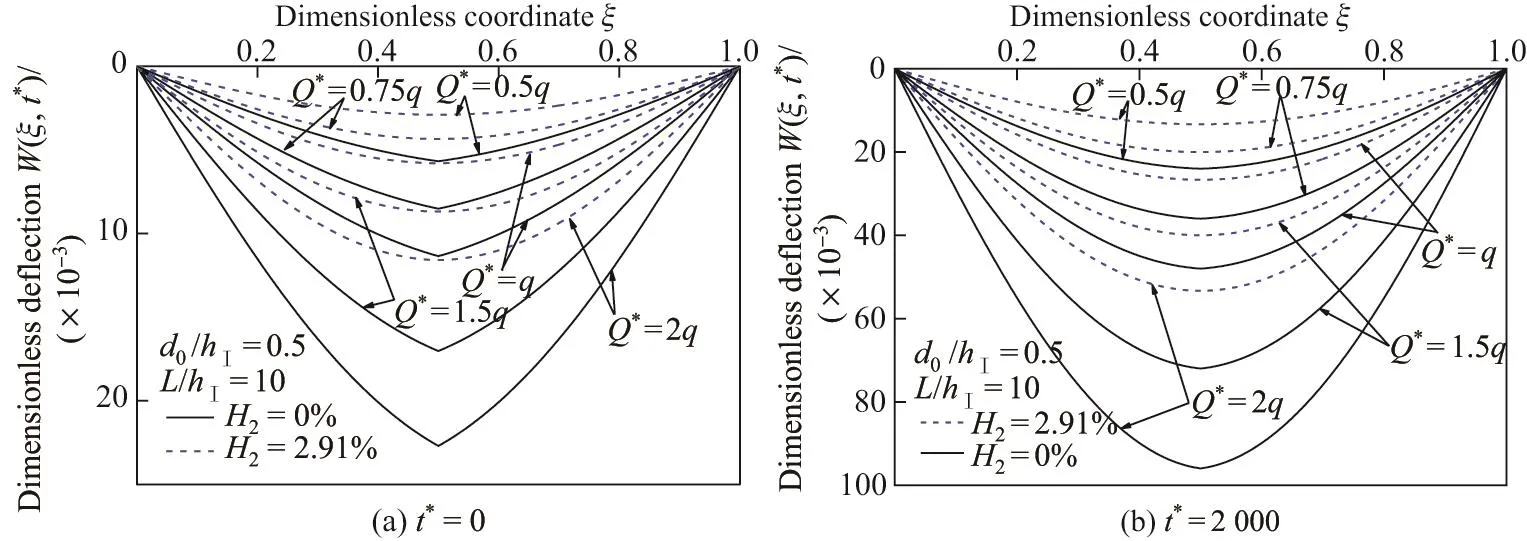
图6 t∗=0和2 000时,不同载荷Q∗下未加固和H2=2.91%的CFRP布加固裂纹DF梁无量纲挠度W(ξ,t∗)的分布Fig.6 Distributions of dimensionless deflections W(ξ,t∗)of unreinforced and H2=2.91%CFRP sheet-reinforced cracked DF beam under different load Q∗ when t∗=0 and 2 000

图7 给出了不同无量纲载荷Q∗和无量纲时刻t∗时,未加固和H2=2.91%的CFRP布加固裂纹DF梁横截面转角φ=dW/(dξ)沿轴线ξ的分布.可见,当t∗=0时,在不同无量纲载荷作用下,未加固裂纹DF梁转角φ在裂纹ξ0=0.5处存在跳跃,并随无量纲载荷Q∗的增加,跳跃值增大,但随着CFRP布加固含量的增加,转角跳跃值减小;当CFRF布加固含量H2达到2.91%时,转角跳跃几乎消失.当t∗=2 000时,在不同无量纲载荷Q∗作用下,ξ0=0.5处的未加固裂纹DF梁转角跳跃值比t∗=0时的转角跳跃值增加1.74%,在端部ξ=0处转角φ比t∗=0时增加387.23%;H2=2.91%的CFRP布加固裂纹DF梁在ξ0=0.5处转角跳跃值在t∗=0和2 000时分别比未加固裂纹DF梁转角跳跃值减少97.50%和96.57%,说明CFRP加固能有效减小DF裂纹梁弯曲变形的横截面转角.

3.2 上表面裂纹梁

假定x0=L/2处的裂纹为上表面裂纹,其他参数同上,图8给出了当Q∗=q=0.484 4时,不同CFRP布加固含量H2下,CFRP布加固简支上表面裂纹DF梁和无裂纹完整DF梁无量纲跨中挠度W(0.5,t∗)随无量纲时间t∗的响应,其中实线为完整DF梁,虚线为上表面裂纹DF梁.为比较方便,图中亦由点虚线给出了下表面裂纹DF梁的无量纲跨中挠度.可见,未加固和CFRP布加固完整/裂纹DF梁的无量纲跨中挠度W(0.5,t∗)随无量纲时间t∗增加而增大,并最终趋于定值.

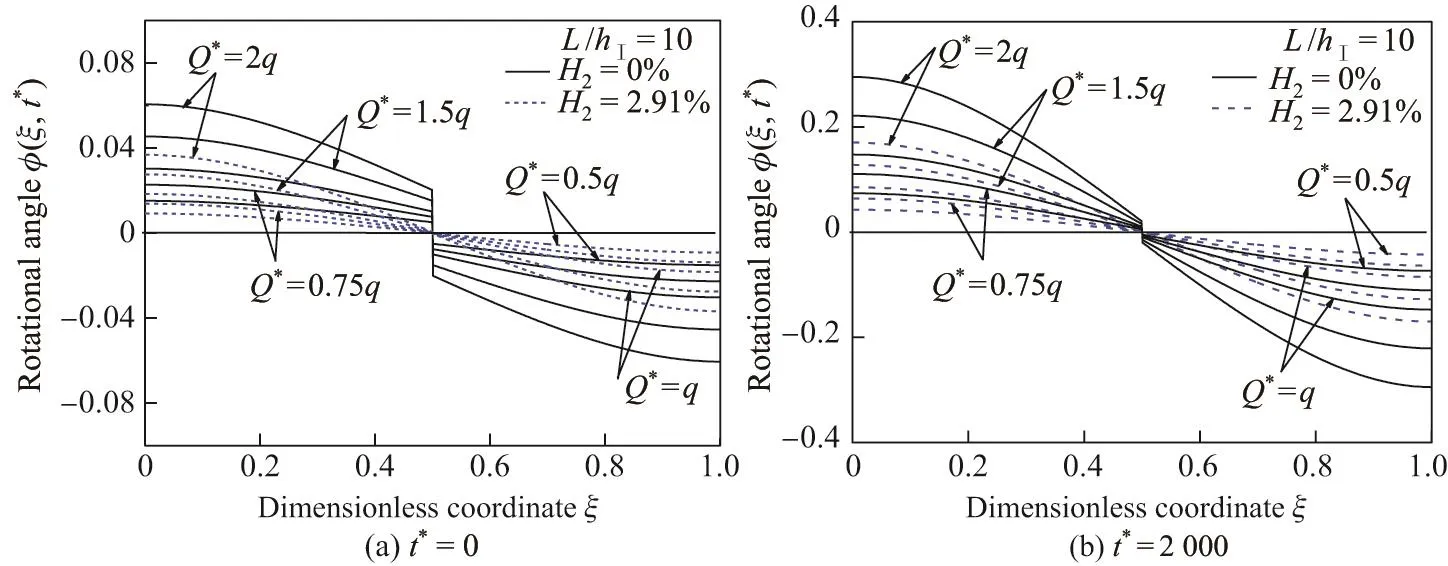
图 7 t∗=0和2 000时,不同载荷Q∗下未加固和H2=2.91%的CFRP布加固裂纹DF梁转角φ(ξ,t∗)的分布Fig.7 Distributions of rotational angle φ(ξ,t∗)of unreinforced and H2=2.91%CFRP sheetreinforced cracked DF beam under different load Q∗ when t∗=0 and t∗=2 000

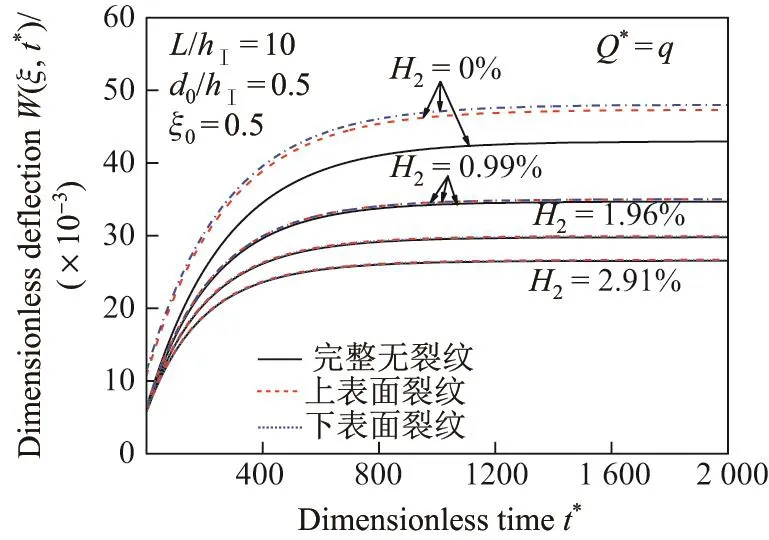
图8 CFRP布加固上/下表面裂纹DF梁和完整DF梁无量纲跨中挠度W(0.5,t∗)随无量纲时间t∗的响应Fig.8 Responses of dimensionless mid-span deflections W(0.5,t∗)vs.dimensionless time t∗of CFRP sheet-reinforced cracked/intact DF beam

另外,对于未加固裂纹DF梁,由式(25)可得裂纹无量纲闭合临界载荷为Q∗CR=QCRL3/E1IⅠ=0.418 9=0.875q,且不依赖于时间t∗,因此在无量纲载荷Q∗=q作用下,未加固上表面裂纹DF梁的裂纹闭合.同时,对比下表面裂纹和上表面裂纹DF梁无量纲跨中挠度W(0.5,t∗)可见,对未加固裂纹DF梁,裂纹开闭状态对裂纹DF梁的无量纲跨中挠度W(0.5,t∗)有明显影响.当H2=0.99%,1.96%和2.91%时,CFRP布加固上表面裂纹的闭合临界载荷分别为Q∗CR=6.52,12.62和18.71,因此在无量纲载荷Q∗作用下,CFRP布加固裂纹DF梁上表面裂纹未闭合,简支下表面裂纹和上表面裂纹DF梁无量纲跨中挠度随时间响应完全相同,而且加固含量H2=2.91%的CFRP布加固裂纹DF梁和无裂纹完整DF梁无量纲跨中挠度基本重合,裂纹效应完全消失.

图9给出了未加固和CFRP布加固简支上表面裂纹DF梁在不同无量纲时间t∗=0和2 000时的无量纲挠度W(ξ,t∗)分布.由于此时的无量纲载荷Q∗=q=0.484 4大于未加固上表面裂纹DF梁的无量纲裂纹闭合临界载荷Q∗CR=0.418 9,故当突加均布载荷在t∗=0作用时,未加固上表面裂纹DF梁裂纹发生闭合.CFRP布加固后,裂纹等效旋转弹簧刚度K0e增大,故闭合临界载荷增大,CFRP布加固含量H2=0.99%和2.91%的裂纹无量纲闭合临界载荷分别为Q∗CR=6.52和18.71,因此当载荷Q∗=q时,H2=0.99%和2.91%的CFRP布加固DF梁的裂纹未闭合,但由于裂纹转角小于裂纹闭合角θ0,故无量纲挠度尖点不明显.

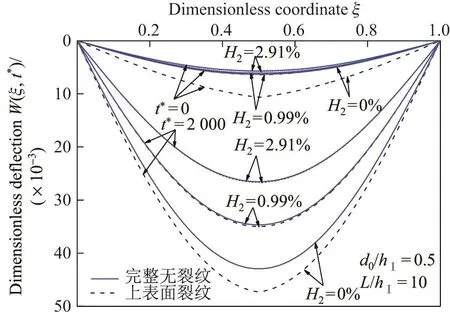
图 9 不同无量纲时刻t∗,CFRP布加固裂纹/完整DF梁无量纲挠度W(ξ,t∗)的分布Fig.9 DistributionsofdimensionlessdeflectionsW(ξ,t∗)ofCFRP sheet-reinforced cracked/intact DF beam for different dimensionless time t∗

图10 给出了t∗=0时,未加固(H2=0%)上表面裂纹DF梁和下表面裂纹DF梁在不同无量纲载荷Q∗下的无量纲挠度W(ξ,t∗)沿轴线ξ的分布,其中虚线和实线分别为上表面裂纹和下表面裂纹的DF梁无量纲挠度.此时,上表面裂纹闭合临界载荷Q∗CR=0.87q=0.418 9,可见当无量纲载荷为Q∗=0.5q和0.75q时,上表面裂纹还未闭合,上表面裂纹DF梁与下表面裂纹DF梁的无量纲挠度W(ξ,t∗)重合;但当Q∗＞Q∗CR时,由于上表面裂纹发生闭合,而下表面裂纹为开裂纹,导致上表面裂纹DF梁与下表面裂纹DF梁的无量纲挠度W(ξ,t∗)出现了明显差异,且上表面裂纹DF梁无量纲挠度小于下表面裂纹DF梁无量纲挠度,说明裂纹闭合可提高裂纹梁的刚度,裂纹开闭状态可显著影响裂纹梁的挠度.类似性质亦存在于CFRP布加固裂纹DF梁的挠度分布中.

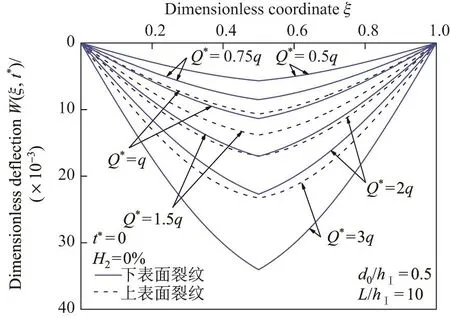
图 10 不同无量纲载荷Q∗下,未加固上/下表面裂纹DF梁无量纲挠度W(ξ,t∗)的分布Fig.10 Distributions of dimensionless deflections W(ξ,t∗)of unreinforced cracked DF beam with a top/bottom surface crack

图11 给出了t∗=0和2 000时,未加固和H2=2.91%的CFRP布加固上表面裂纹DF梁在不同无量纲载荷Q∗下横截面转角φ=dW/(dξ)沿轴线ξ的分布.可见,未加固裂纹DF梁的转角φ存在跳跃.当Q∗＜Q∗CR时,即当载荷Q∗未达到裂纹闭合临界载荷Q∗CR时,随着载荷Q∗的增加,裂纹ξ0=0.5处转角φ跳跃值增大;但当Q∗≥Q∗CR时,即载荷Q∗超过裂纹闭合临界载荷Q∗CR时,裂纹ξ0=0.5处转角φ的跳跃值保持为常量θ0=1°,即裂纹的初始张开角θ0.对于H2=2.91%的CFRP布加固裂纹DF梁,由于加固裂纹等效旋转弹簧刚度增大,加固后裂纹闭合无量纲临界载荷变为Q∗CR=38.63q,故CFRP布加固裂纹DF梁在裂纹ξ0=0.5处转角φ的跳跃值小于θ0=1°,且随载荷Q∗的增加而增大.同时,经计算发现,这些性质对其他裂纹位置ξ0和深度d0/hⅠ亦成立.

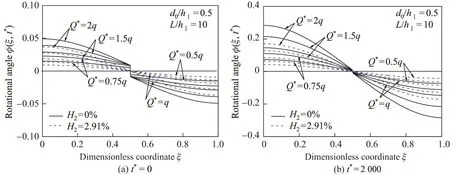
图 11 t∗=0和2 000时,不同载荷Q∗下未加固和H2=2.91%的CFRP布加固裂纹DF梁转角φ(ξ,t∗)的分布Fig.11 Distributions of rotational angles φ(ξ,t∗)of unreinforced and H2=2.91%CFRP sheetreinforced cracked DF beam under different load Q∗ when t∗ =0 and t∗=2 000

取L/hⅠ=20,其他参数保持不变,则无量纲载荷q=Q0L3/(E1IⅠ)=3.875 3,由式(25)可得未加固裂纹DF梁无量纲裂纹闭合临界载荷Q∗CR=0.216q.图12给出了L/hⅠ=20,t∗=0时,未加固和不同H2的CFRP布加固裂纹DF梁在不同无量纲载荷Q∗下无量纲挠度W(ξ,t∗)沿轴线ξ的分布.可见,未加固裂纹DF梁无量纲挠度W(ξ,t∗)在裂纹ξ0=0.5处呈现尖点,但CFRP布加固的裂纹DF梁无量纲挠度在裂纹ξ0=0.5处尖点不明显,且H2=0.99%的CFRP布加固裂纹DF梁无量纲挠度大于H2=2.91%的CFRP布加固裂纹DF梁无量纲挠度,即增加CFRP布加固含量H2可减少CFRP布加固裂纹DF梁弯曲变形.经计算发现,对不同时刻t∗,上述性质亦成立.

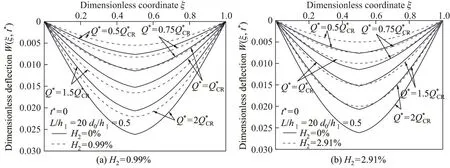
图 12 L/hⅠ=20,t∗=0时,不同H2下未加固和CFRP布加固裂纹DF梁无量纲挠度W(ξ,t∗)的分布Fig.12 Distributions of dimensionless deflection W(ξ,t∗)of unreinforced and CFRP sheetreinforced cracked DF beam when L/hⅠ=20 and t∗ =0 for different H2

4 结论

本工作采用开闭裂纹模型,考虑裂纹缝隙效应,将裂纹等效为非线性旋转弹簧,给出了FRP布加固裂纹梁的裂纹等效旋转弹簧刚度.将FRP布加固黏弹性梁在裂纹处分段,利用梁弯曲的边界条件和裂纹处的连接条件,借助Laplace变换及逆变换,给出均布突加载荷作用下FRP布加固简支裂纹黏弹性梁弯曲变形的解析解.数值分析了CFRP布加固上/下表面裂纹黏弹性DF梁的弯曲变形,考察了CFRP布含量、梁跨高比、裂纹位置及其开闭状态等对CFRP布加固裂纹DF梁弯曲蠕变的影响,得到如下结论.

(1)FRP布加固裂纹的等效旋转弹簧刚度和裂纹闭合临界载荷依赖于裂纹深度和FRP的材料参数等,FRP布加固裂纹的等效旋转弹簧刚度值随裂纹深度的减小以及FRP材料弹性模量和含量增加而增大.

(2)FRP布加固不仅能有效减小梁的初始弹性挠度和蠕变稳态挠度,而且可以显著降低裂纹对DF梁弯曲变形的影响.

(3)梁弯曲挠度分布在裂纹处存在尖点,且对于开裂纹,当载荷较小时,挠度在裂缝处的尖点现象并不明显,但随着载荷的增加,尖点现象愈加明显.同时,梁横截面转角在裂纹处发生突变,转角不连续.

(4)对于CFRP布加固简支下表面裂纹DF梁,裂纹处转角跳跃值随载荷增加而增大,随着CFRP布加固含量H2的增加,CFRP布加固裂纹梁的挠度减小,且裂纹效应逐渐减弱,最后几乎完全消失.

(5)对于CFRP布加固简支上表面裂纹DF梁,当载荷小于裂纹闭合临界载荷时,裂纹处转角跳跃值随载荷增加而增大,当载荷达到裂纹闭合临界载荷时,裂纹处转角跳跃值保持为常量,即为裂纹初始张开角度.